13.1轴对称 学案(含答案) 2024—2025学年人教版数学八年级上册
文档属性
| 名称 | 13.1轴对称 学案(含答案) 2024—2025学年人教版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 542.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 00:00:00 | ||
图片预览


文档简介
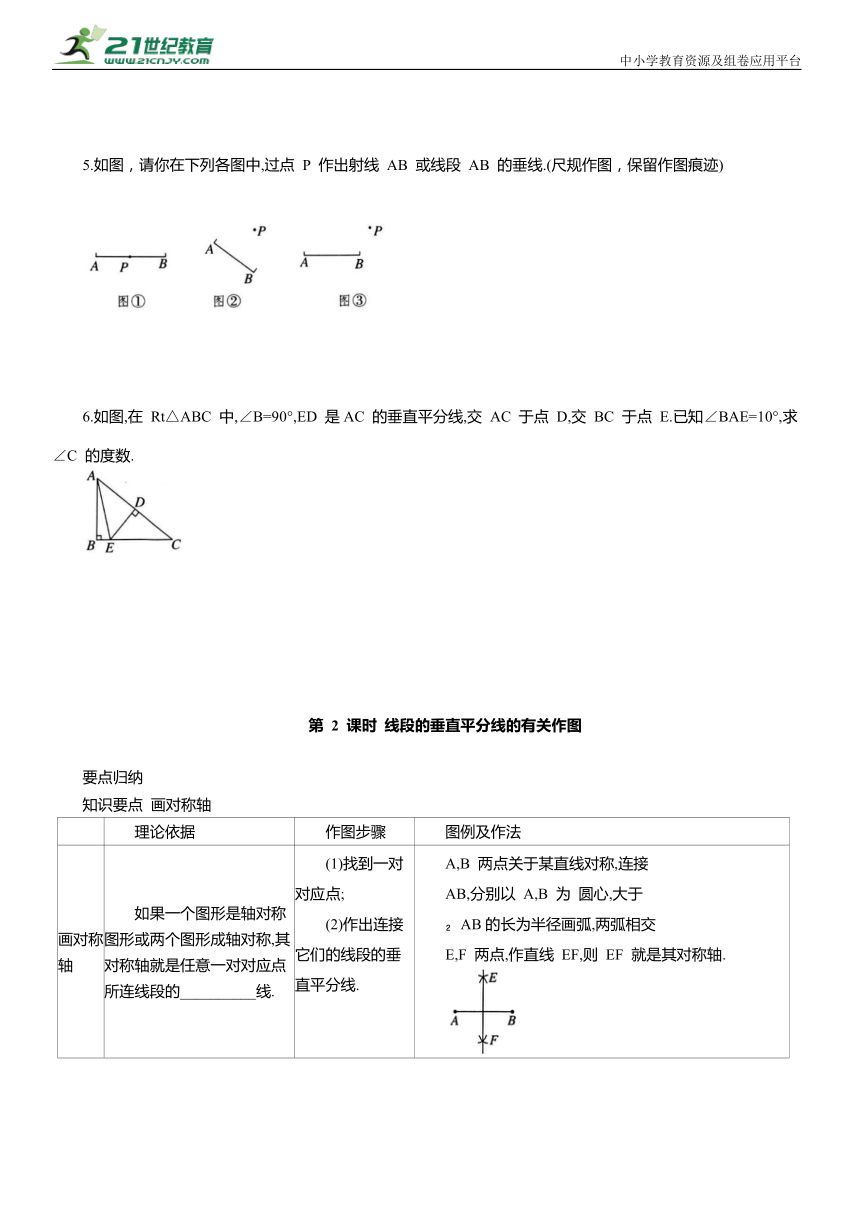
13.1轴对称
13.1.1轴对称
要点归纳
知识要点1 垂直平分线的概念
经过线段中点并且 于这条线段的直线叫做这条线段的垂直平分线.
知识要点 2 轴对称图形与轴对称
相关概念 性质
轴对称图形 如果一个平面图形沿一条直线折叠,直线两旁的部分能够__________,这个图形就叫做轴对称图形,这条直线就是它的__________. 轴对称图形的对称轴是任何一对对应点所连线段的____________线.如 图,l垂直平分 BC、B C 、B C .
轴对称 把一个图形沿着某一条直线折叠,如果它能够与另一个图形_______,那么就说这两个图形关于这条直线对称,这条直线叫做_________,折叠后重合的点是对应点,叫做对称点. 如果两个图形关于某条直线 对称,那么对称轴是任何一 对对应点所连线段的垂直平 分线.如图,l 垂直平分 AA'、BB'、CC'.
当堂检测 (建议用时:10分钟)
1.下列图形中不是轴对称图形的是 ( )
2.正方形的对称轴有 ( )
A.1 条 B.2条
C.3 条 D.4 条
3.如图,△ABC 与△DEF 关于直线l 对称,AB=4,BC=6,△DEF 的周长是 18.①AC的长为 ;②若∠B=110°,∠A=46°,则∠F= .
4.如图,△ABC 和△A'B'C'关于直线m 对称.
(1)结合图形指出对称点;
(2)连接 AA',直线m 与线段 AA'有什么关系
(3)延长线段AC 与A'C',它们的交点与直线m有什么关系
13.1.2 线段的垂直平分线的性质
第 1课时 线段的垂直平分线的性质与判定
要点归纳
知识要点 线段的垂直平分线的性质与判定
内容 图例
性质 线段垂直平分线上的点与这条线段两个端点的距离________. 如图,直线 l 是线段 AB 的垂直 平分线,点 P 为 l 上一点,则 PA=PB;反过来,若 PA = PB,则点 P 在线段AB 的垂直平分线上.
判定 与线段两个端点距离相等的点在这条线段的____________上.
拓展 三角形三边的垂直平分线交于一点,这点到三角形三个顶点的距离相等.
当堂检测 (建议用时:10分钟)
1.如图,在△ABC中,AB 的垂直平分线交 AC于点 P.已知 PA=5,则线段 PB的长度为( )
A.8 B.7 C.6 D.5
2.若点 P 为△ABC 内部一点,且 PA=PB=PC,则点 P 是△ABC 的 ( )
A.三条中线的交点
B.三条内角平分线的交点
C.三条高的交点
D.三条垂直平分线的交点
3.如图所示的仪器中,OD=OE,CD=CE.小州把这个仪器放在直线 l 上,使点 D、E 落在直线l 上,作直线 OC,则 OC⊥l,其中蕴含的道理是 .
4.如图,△ABC 的边 BC 的垂直平分线 MN 交 AC于 D.若△ADB 的周长是10cm,AB=4cm,则AC= cm.
5.如图,请你在下列各图中,过点 P 作出射线 AB 或线段 AB 的垂线.(尺规作图,保留作图痕迹)
6.如图,在 Rt△ABC 中,∠B=90°,ED 是AC 的垂直平分线,交 AC 于点 D,交 BC 于点 E.已知∠BAE=10°,求∠C 的度数.
第 2 课时 线段的垂直平分线的有关作图
要点归纳
知识要点 画对称轴
理论依据 作图步骤 图例及作法
画对称轴 如果一个图形是轴对称图形或两个图形成轴对称,其对称轴就是任意一对对应点所连线段的__________线. (1)找到一对对应点; (2)作出连接它们的线段的垂直平分线. A,B 两点关于某直线对称,连接 AB,分别以 A,B 为 圆心,大于 AB的长为半径画弧,两弧相交 E,F 两点,作直线 EF,则 EF 就是其对称轴.
中小学教育资源及组卷应用平台
当堂检测 (建议用时:10分钟)
1.如图,在△ABC 中,分别以点 A,B 为圆心,大于 AB 长为半径画弧,两弧分别交于点D,E,则直线 DE 是 ( )
A.∠A 的平分线
B. AC 边的中线
C. BC 边的高线
D. AB 边的垂直平分线
2.通过如下尺规作图,能确定点 D 是 BC 边中点的是 ( )
3.如图,正五边形ABCDE 是轴对称图形,连接 BE,作 BE 的 l,则直线 l是正五边形ABCDE 的对称轴.
4.下列图形是轴对称图形吗 若是,画出它们的对称轴.
5.如图,直线 m 表示一条公路,A、B 表示两所大学.要在公路旁修建一个车站 P 使其到两所大学的距离相等,请在图上找出这点P(尺规作图,不写作法,保留作图痕迹).
13.1 轴对称
13.1.1 轴对称
要点归纳
知识要点1:垂直
知识要点2:互相重合 对称轴 垂直平分重合 对称轴
当堂检测
1. C 2. D 3.8 24°
4.解:(1)由图可知,对称点有 A 和A',B 和B',C 和C'.
(2)直线 m 垂直平分线段AA'.
(3)它们的交点在直线 m 上.
13.1.2 线段的垂直平分线的性质
第 1 课时 线段的垂直平分线的性质与判定要点归纳
知识要点:相等 垂直平分线
当堂检测
1. D 2. D
3.与线段两个端点距离相等的点在这条线段的垂直平分线上
4.6
5.解:如图所示.
6.解:∵∠B=90°,∠BAE=10°,∴∠BEA=80°.∵ED 是AC 的垂直平分线,∴△AEC关 于 直 线 ED 对 称. ∴∠C= ∠EAC.∵∠BEA=∠C+∠EAC,∴∠C=40°.
第 2 课时 线段的垂直平分线的有关作图要点归纳
知识要点:垂直平分
当堂检测
1. D 2. B 3.垂直平分线
4.解:三个图形都是轴对称图形,对称轴略.
5.解:如图,点 P 是线段 AB 的垂直平分线与直线m的交点.
13.1.1轴对称
要点归纳
知识要点1 垂直平分线的概念
经过线段中点并且 于这条线段的直线叫做这条线段的垂直平分线.
知识要点 2 轴对称图形与轴对称
相关概念 性质
轴对称图形 如果一个平面图形沿一条直线折叠,直线两旁的部分能够__________,这个图形就叫做轴对称图形,这条直线就是它的__________. 轴对称图形的对称轴是任何一对对应点所连线段的____________线.如 图,l垂直平分 BC、B C 、B C .
轴对称 把一个图形沿着某一条直线折叠,如果它能够与另一个图形_______,那么就说这两个图形关于这条直线对称,这条直线叫做_________,折叠后重合的点是对应点,叫做对称点. 如果两个图形关于某条直线 对称,那么对称轴是任何一 对对应点所连线段的垂直平 分线.如图,l 垂直平分 AA'、BB'、CC'.
当堂检测 (建议用时:10分钟)
1.下列图形中不是轴对称图形的是 ( )
2.正方形的对称轴有 ( )
A.1 条 B.2条
C.3 条 D.4 条
3.如图,△ABC 与△DEF 关于直线l 对称,AB=4,BC=6,△DEF 的周长是 18.①AC的长为 ;②若∠B=110°,∠A=46°,则∠F= .
4.如图,△ABC 和△A'B'C'关于直线m 对称.
(1)结合图形指出对称点;
(2)连接 AA',直线m 与线段 AA'有什么关系
(3)延长线段AC 与A'C',它们的交点与直线m有什么关系
13.1.2 线段的垂直平分线的性质
第 1课时 线段的垂直平分线的性质与判定
要点归纳
知识要点 线段的垂直平分线的性质与判定
内容 图例
性质 线段垂直平分线上的点与这条线段两个端点的距离________. 如图,直线 l 是线段 AB 的垂直 平分线,点 P 为 l 上一点,则 PA=PB;反过来,若 PA = PB,则点 P 在线段AB 的垂直平分线上.
判定 与线段两个端点距离相等的点在这条线段的____________上.
拓展 三角形三边的垂直平分线交于一点,这点到三角形三个顶点的距离相等.
当堂检测 (建议用时:10分钟)
1.如图,在△ABC中,AB 的垂直平分线交 AC于点 P.已知 PA=5,则线段 PB的长度为( )
A.8 B.7 C.6 D.5
2.若点 P 为△ABC 内部一点,且 PA=PB=PC,则点 P 是△ABC 的 ( )
A.三条中线的交点
B.三条内角平分线的交点
C.三条高的交点
D.三条垂直平分线的交点
3.如图所示的仪器中,OD=OE,CD=CE.小州把这个仪器放在直线 l 上,使点 D、E 落在直线l 上,作直线 OC,则 OC⊥l,其中蕴含的道理是 .
4.如图,△ABC 的边 BC 的垂直平分线 MN 交 AC于 D.若△ADB 的周长是10cm,AB=4cm,则AC= cm.
5.如图,请你在下列各图中,过点 P 作出射线 AB 或线段 AB 的垂线.(尺规作图,保留作图痕迹)
6.如图,在 Rt△ABC 中,∠B=90°,ED 是AC 的垂直平分线,交 AC 于点 D,交 BC 于点 E.已知∠BAE=10°,求∠C 的度数.
第 2 课时 线段的垂直平分线的有关作图
要点归纳
知识要点 画对称轴
理论依据 作图步骤 图例及作法
画对称轴 如果一个图形是轴对称图形或两个图形成轴对称,其对称轴就是任意一对对应点所连线段的__________线. (1)找到一对对应点; (2)作出连接它们的线段的垂直平分线. A,B 两点关于某直线对称,连接 AB,分别以 A,B 为 圆心,大于 AB的长为半径画弧,两弧相交 E,F 两点,作直线 EF,则 EF 就是其对称轴.
中小学教育资源及组卷应用平台
当堂检测 (建议用时:10分钟)
1.如图,在△ABC 中,分别以点 A,B 为圆心,大于 AB 长为半径画弧,两弧分别交于点D,E,则直线 DE 是 ( )
A.∠A 的平分线
B. AC 边的中线
C. BC 边的高线
D. AB 边的垂直平分线
2.通过如下尺规作图,能确定点 D 是 BC 边中点的是 ( )
3.如图,正五边形ABCDE 是轴对称图形,连接 BE,作 BE 的 l,则直线 l是正五边形ABCDE 的对称轴.
4.下列图形是轴对称图形吗 若是,画出它们的对称轴.
5.如图,直线 m 表示一条公路,A、B 表示两所大学.要在公路旁修建一个车站 P 使其到两所大学的距离相等,请在图上找出这点P(尺规作图,不写作法,保留作图痕迹).
13.1 轴对称
13.1.1 轴对称
要点归纳
知识要点1:垂直
知识要点2:互相重合 对称轴 垂直平分重合 对称轴
当堂检测
1. C 2. D 3.8 24°
4.解:(1)由图可知,对称点有 A 和A',B 和B',C 和C'.
(2)直线 m 垂直平分线段AA'.
(3)它们的交点在直线 m 上.
13.1.2 线段的垂直平分线的性质
第 1 课时 线段的垂直平分线的性质与判定要点归纳
知识要点:相等 垂直平分线
当堂检测
1. D 2. D
3.与线段两个端点距离相等的点在这条线段的垂直平分线上
4.6
5.解:如图所示.
6.解:∵∠B=90°,∠BAE=10°,∴∠BEA=80°.∵ED 是AC 的垂直平分线,∴△AEC关 于 直 线 ED 对 称. ∴∠C= ∠EAC.∵∠BEA=∠C+∠EAC,∴∠C=40°.
第 2 课时 线段的垂直平分线的有关作图要点归纳
知识要点:垂直平分
当堂检测
1. D 2. B 3.垂直平分线
4.解:三个图形都是轴对称图形,对称轴略.
5.解:如图,点 P 是线段 AB 的垂直平分线与直线m的交点.
