第十三章轴对称单元测试卷(含答案) 2024—2025学年人教版数学八年级上册
文档属性
| 名称 | 第十三章轴对称单元测试卷(含答案) 2024—2025学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 591.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 06:32:29 | ||
图片预览



文档简介
第十三章轴对称单元测试卷
满分:120分 时间:120分钟 得分:
一、选择题(每小题 3分,共30分)
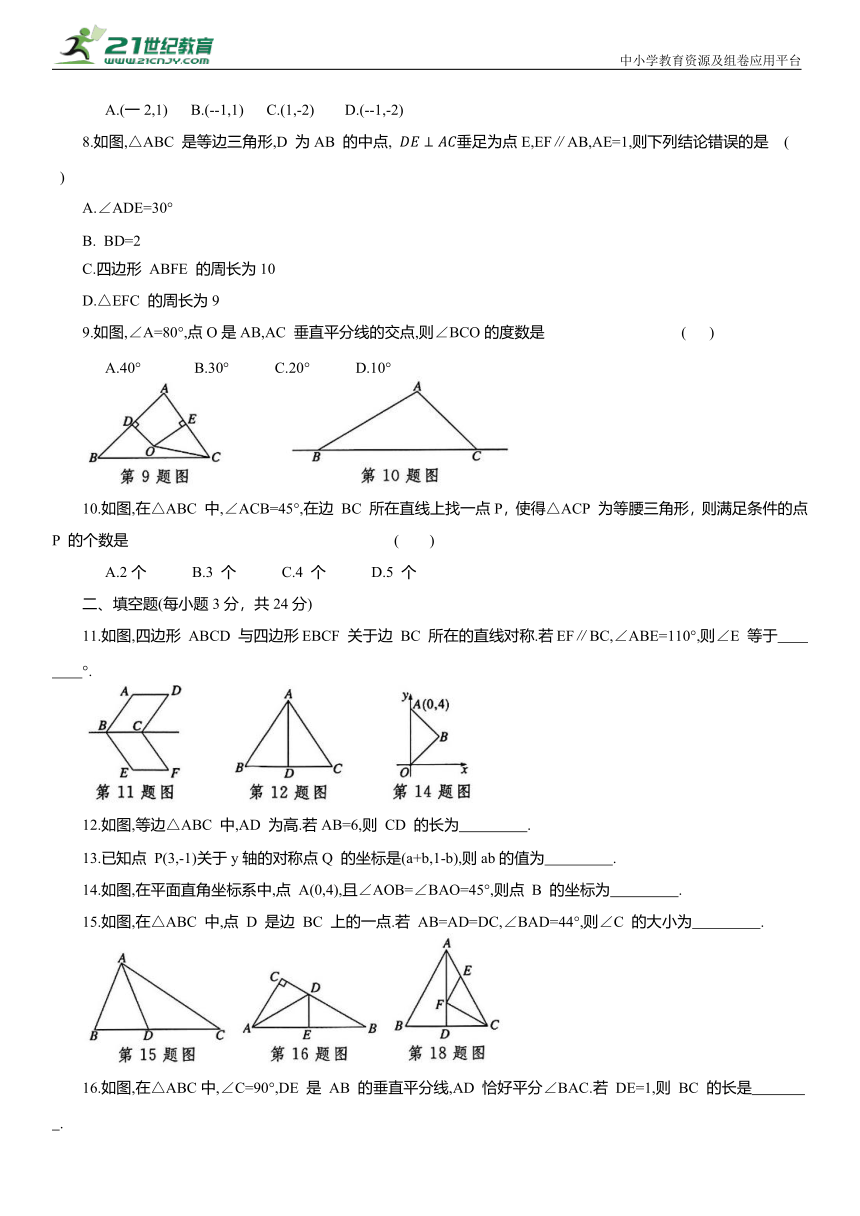
1.下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是 ( )
2.如图,点 C 在 AD 上, 则 的度数为 ( )
3.如图,在 中,AB 的垂直平分线分别交AB、BC于点D、E,连接AE.若 则 BC 的长是 ( )
A.2 B.4 C.6 D.8
4.数学活动课上,四位同学围绕作图问题:“如图,已知直线l和l 外一点 P,用直尺和圆规作直线 PQ,使. 于点Q”,分别作出了下列四个图形,其中作法错误的是 ( )
5.如图,一艘海轮位于灯塔 P 的南偏东 方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔 P 的北偏东 方向的 N 处,则 N 处与灯塔 P的距离为 ( )
A.40海里 B.60海里 C.70海里 D.80 海里
6.若等腰三角形的顶角是大于 的锐角,则底角度数可以是 ( )
A.30° B.45°
7.小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用 表示,右下角方子的位置用(0,-1)表示.小莹将第4 枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是 ( )
A.(一2,1) B.(--1,1) C.(1,-2) D.(--1,-2)
8.如图,△ABC 是等边三角形,D 为AB 的中点, 垂足为点E,EF∥AB,AE=1,则下列结论错误的是 ( )
A.∠ADE=30°
B. BD=2
C.四边形 ABFE 的周长为10
D.△EFC 的周长为9
9.如图,∠A=80°,点O是AB,AC 垂直平分线的交点,则∠BCO的度数是 ( )
A.40° B.30° C.20° D.10°
10.如图,在△ABC 中,∠ACB=45°,在边 BC 所在直线上找一点P,使得△ACP 为等腰三角形,则满足条件的点P 的个数是 ( )
A.2个 B.3 个 C.4 个 D.5 个
二、填空题(每小题3分,共24分)
11.如图,四边形 ABCD 与四边形EBCF 关于边 BC 所在的直线对称.若EF∥BC,∠ABE=110°,则∠E 等于 °.
12.如图,等边△ABC 中,AD 为高.若AB=6,则 CD 的长为 .
13.已知点 P(3,-1)关于y轴的对称点Q 的坐标是(a+b,1-b),则ab的值为 .
14.如图,在平面直角坐标系中,点 A(0,4),且∠AOB=∠BAO=45°,则点 B 的坐标为 .
15.如图,在△ABC 中,点 D 是边 BC 上的一点.若 AB=AD=DC,∠BAD=44°,则∠C 的大小为 .
16.如图,在△ABC中,∠C=90°,DE 是 AB 的垂直平分线,AD 恰好平分∠BAC.若 DE=1,则 BC 的长是 .
17.规定:等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”,记作k.若 则该等腰三角形的顶角为 .
18.如图,在△ABC 中,. AD 是△ABC的中线,F 是AD 上的动点,E 是AC 边上的动点,则CF+EF 的最小值为 .
三、解答题(共 66 分)
19.(8 分)如图,已知 OC 是∠AOB 的平分线,将直尺DEMN 的EM边与OB 边重合,顶点 D 落在OA 边上,DN 边与OC 交于点 P.
(1)猜想△DOP 是 三角形;
(2)证明你的猜想,写出解答过程.
20.(8分)如图,在边长为1 的小正方形网格中,△AOB 的顶点均在格点上.
(1)A 点关于y 轴的对称点 P 的坐标为 ;
(2)作△AOB 关于x 轴对称的
(3)在(2)的条件下,点. 的坐标为 ,用一句话描述点 P 的坐标和点. 的坐标之间的关系:
21.(8分)如图,在△ABC中,AB=AC,BE⊥AC 于点E,D 为AB 上一点,△BDE 是正三角形.
(1)求∠C 的度数;
(2)若 DE=3cm,求 AB 的长.
22.(10分)如图,在△ABC中,AD⊥BC,EF 垂直平分AC,交 AC 于点 F,交 BC于点E,且 BD=DE,连接AE.
(1)若∠BAE=40°,求∠C 的度数;
(2)若△ABC 的周长为 14cm,AC=6cm,求 DC 的长.
23.(10分)已知:如图,
(1)按要求作图:作AB 的垂直平分线MN 交AC 于N,交AB 于M,连接BN(不写作法,保留作图痕迹);
(2)下列结论:①BN 是 的平分线;( 是等腰三角形;( .其中正确的有 (填序号);
(3)从你认为正确的结论中选一个加以证明.
24.(10分)如图,在等边 中,点 D、E 分别在边 BC、AC 上,且 AD、BE 交于点P, 于Q.
(1)求证:
(2)连接PC,若 求 的值.
25.(12 分)直角三角形纸片 ABC 中, 如图,将纸片沿某条直线折叠,使点 A 落在直角边 BC上,记落点为 D,设折痕与 AB、AC 边分别交于点 E、F.
(1)如果 求 的度数;
(2)若折叠后的 与 均为等腰三角形,那么纸片中 的度数是多少 写出你的计算过程,并画出符合条件的折叠后的图形.
中小学教育资源及组卷应用平台
1. D 2. C 3. C 4. A 5. D
6. C 7. B 8. C 9. D 10. C
11.125 12.3 13.—10 14.(2,2)
15.34°16.3 17.45°18.
19.(1)等腰(3分)
(2)证明:∵OC 平分∠AOB,∴∠DOP =∠BOP.∵DN∥EM,∴∠DPO=∠BOP.∴∠DOP=∠DPO.∴OD=PD.∴△DOP是等腰三角形.(8分)
20.解:(1)(--1,3)(2分)
(2)图略.(4分)
(3)(1,-3) 点 P 的横坐标与纵坐标分别和点 A 的横坐标与纵坐标互为相反数(8分)
21.解:(1)∵△BDE 是正三角形,∴∠DBE=60°.∵BE⊥AC,∴∠BEA=90°.∴∠A=90°- 60°= 30°. ∵AB= AC, ∴∠C= (4分)
(2) 由(1) 知∠A = 30°,∠BEA = 90°,∴AB= 2BE. 又△BDE 为 正 三 角 形,∴BE=DE=3cm.∴AB=2×3=6(cm).(8分)
22.解:(1)∵AD⊥BE,BD=DE,EF 垂直平分 AC,∴AB=AE=EC.∴∠AED =∠B,∠C = ∠CAE.∵∠BAE = 40°, (3 分)
(5分)
(2)∵△ABC 的周长为 14 cm,AC=6 cm,∴AB+BE+EC=8cm,即 2DE+2EC=8 cm.(8 分)∴ DC = DE + EC = 4 cm.(10分)
23.解:(1)如图.(3分)
(2)①②(6分)
(3)答案不唯一,如选择结论①BN 是∠ABC
的平分线.证明如下:∵AB=AC,∠A=36°,
∵MN 垂直平分AB,∴NA=NB.∴∠ABN=
∠A=36°.∴∠CBN=∠ABC-∠ABN=36°.
∴∠CBN=∠ABN.∴BN 是∠ABC 的平分
线.(10分)
24.(1) 证明:在等 边 △ABC 中,AB =AC,∠BAE=∠ACD=60°.△BAE≌△ACD
∴∠ABE = ∠CAD.∴∠BPQ =∠ABE + ∠BAP = ∠CAD + ∠BAP =∠BAC=60°.∵BQ⊥AD 于 Q,∴∠BQP=90°.∴∠PBQ=30°.∴BP=2PQ.(5分)
(2)解:∵∠ABE =∠CAD,∴∠ABC=∠ABE = ∠BAC- ∠CAD,即∠PBC =∠BAQ.∵△ABC 是等边三角形,∴AB=BC.∵BQ⊥AD,BP⊥PC,∴∠BQA =∠CPB = 90°. 在 △BAQ 和 △CBP 中,
.∴AQ=BP=2PQ.∴AP=PQ,即 (10)分)
25.解:(1)根据翻折可知∠AFE=∠DFE= ∵∠C=90°,∴∠CDF =90°—50°=40°.(3 分)
(2)∵△CDF 中,∠C=90°,且△CDF 是等腰 三 角 形, ∴CF= CD. ∴ ∠CFD =∠CDF=45°.连接 AD.设∠DAE=x.由对称性可知AF=FD,AE=DE,∴∠FDA= ∠CFD = 22.5°,∠ADE =∠DAE =x,∠DEB=2∠DAE=2x.(5分)
① 如 图 ①, 当 DE = DB 时,∠B =∠DEB=2x.由∠CDE=∠DEB+∠B,得 解得x=22.5°.此时∠B=2x=45°.(7分)
②如图②,当BD=BE时,则∠B=180°=4x.由∠CDE =∠DEB+∠B,得 解得x=37.5°.此时∠ .(9分)
③当 DE =BE 时,则 由∠CDE=∠DEB+∠B,得( 此方程无解.∴DE=BE 不成立.(11 分)综上所述,∠B =45°或 30°.(12分)
满分:120分 时间:120分钟 得分:
一、选择题(每小题 3分,共30分)
1.下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是 ( )
2.如图,点 C 在 AD 上, 则 的度数为 ( )
3.如图,在 中,AB 的垂直平分线分别交AB、BC于点D、E,连接AE.若 则 BC 的长是 ( )
A.2 B.4 C.6 D.8
4.数学活动课上,四位同学围绕作图问题:“如图,已知直线l和l 外一点 P,用直尺和圆规作直线 PQ,使. 于点Q”,分别作出了下列四个图形,其中作法错误的是 ( )
5.如图,一艘海轮位于灯塔 P 的南偏东 方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔 P 的北偏东 方向的 N 处,则 N 处与灯塔 P的距离为 ( )
A.40海里 B.60海里 C.70海里 D.80 海里
6.若等腰三角形的顶角是大于 的锐角,则底角度数可以是 ( )
A.30° B.45°
7.小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用 表示,右下角方子的位置用(0,-1)表示.小莹将第4 枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是 ( )
A.(一2,1) B.(--1,1) C.(1,-2) D.(--1,-2)
8.如图,△ABC 是等边三角形,D 为AB 的中点, 垂足为点E,EF∥AB,AE=1,则下列结论错误的是 ( )
A.∠ADE=30°
B. BD=2
C.四边形 ABFE 的周长为10
D.△EFC 的周长为9
9.如图,∠A=80°,点O是AB,AC 垂直平分线的交点,则∠BCO的度数是 ( )
A.40° B.30° C.20° D.10°
10.如图,在△ABC 中,∠ACB=45°,在边 BC 所在直线上找一点P,使得△ACP 为等腰三角形,则满足条件的点P 的个数是 ( )
A.2个 B.3 个 C.4 个 D.5 个
二、填空题(每小题3分,共24分)
11.如图,四边形 ABCD 与四边形EBCF 关于边 BC 所在的直线对称.若EF∥BC,∠ABE=110°,则∠E 等于 °.
12.如图,等边△ABC 中,AD 为高.若AB=6,则 CD 的长为 .
13.已知点 P(3,-1)关于y轴的对称点Q 的坐标是(a+b,1-b),则ab的值为 .
14.如图,在平面直角坐标系中,点 A(0,4),且∠AOB=∠BAO=45°,则点 B 的坐标为 .
15.如图,在△ABC 中,点 D 是边 BC 上的一点.若 AB=AD=DC,∠BAD=44°,则∠C 的大小为 .
16.如图,在△ABC中,∠C=90°,DE 是 AB 的垂直平分线,AD 恰好平分∠BAC.若 DE=1,则 BC 的长是 .
17.规定:等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”,记作k.若 则该等腰三角形的顶角为 .
18.如图,在△ABC 中,. AD 是△ABC的中线,F 是AD 上的动点,E 是AC 边上的动点,则CF+EF 的最小值为 .
三、解答题(共 66 分)
19.(8 分)如图,已知 OC 是∠AOB 的平分线,将直尺DEMN 的EM边与OB 边重合,顶点 D 落在OA 边上,DN 边与OC 交于点 P.
(1)猜想△DOP 是 三角形;
(2)证明你的猜想,写出解答过程.
20.(8分)如图,在边长为1 的小正方形网格中,△AOB 的顶点均在格点上.
(1)A 点关于y 轴的对称点 P 的坐标为 ;
(2)作△AOB 关于x 轴对称的
(3)在(2)的条件下,点. 的坐标为 ,用一句话描述点 P 的坐标和点. 的坐标之间的关系:
21.(8分)如图,在△ABC中,AB=AC,BE⊥AC 于点E,D 为AB 上一点,△BDE 是正三角形.
(1)求∠C 的度数;
(2)若 DE=3cm,求 AB 的长.
22.(10分)如图,在△ABC中,AD⊥BC,EF 垂直平分AC,交 AC 于点 F,交 BC于点E,且 BD=DE,连接AE.
(1)若∠BAE=40°,求∠C 的度数;
(2)若△ABC 的周长为 14cm,AC=6cm,求 DC 的长.
23.(10分)已知:如图,
(1)按要求作图:作AB 的垂直平分线MN 交AC 于N,交AB 于M,连接BN(不写作法,保留作图痕迹);
(2)下列结论:①BN 是 的平分线;( 是等腰三角形;( .其中正确的有 (填序号);
(3)从你认为正确的结论中选一个加以证明.
24.(10分)如图,在等边 中,点 D、E 分别在边 BC、AC 上,且 AD、BE 交于点P, 于Q.
(1)求证:
(2)连接PC,若 求 的值.
25.(12 分)直角三角形纸片 ABC 中, 如图,将纸片沿某条直线折叠,使点 A 落在直角边 BC上,记落点为 D,设折痕与 AB、AC 边分别交于点 E、F.
(1)如果 求 的度数;
(2)若折叠后的 与 均为等腰三角形,那么纸片中 的度数是多少 写出你的计算过程,并画出符合条件的折叠后的图形.
中小学教育资源及组卷应用平台
1. D 2. C 3. C 4. A 5. D
6. C 7. B 8. C 9. D 10. C
11.125 12.3 13.—10 14.(2,2)
15.34°16.3 17.45°18.
19.(1)等腰(3分)
(2)证明:∵OC 平分∠AOB,∴∠DOP =∠BOP.∵DN∥EM,∴∠DPO=∠BOP.∴∠DOP=∠DPO.∴OD=PD.∴△DOP是等腰三角形.(8分)
20.解:(1)(--1,3)(2分)
(2)图略.(4分)
(3)(1,-3) 点 P 的横坐标与纵坐标分别和点 A 的横坐标与纵坐标互为相反数(8分)
21.解:(1)∵△BDE 是正三角形,∴∠DBE=60°.∵BE⊥AC,∴∠BEA=90°.∴∠A=90°- 60°= 30°. ∵AB= AC, ∴∠C= (4分)
(2) 由(1) 知∠A = 30°,∠BEA = 90°,∴AB= 2BE. 又△BDE 为 正 三 角 形,∴BE=DE=3cm.∴AB=2×3=6(cm).(8分)
22.解:(1)∵AD⊥BE,BD=DE,EF 垂直平分 AC,∴AB=AE=EC.∴∠AED =∠B,∠C = ∠CAE.∵∠BAE = 40°, (3 分)
(5分)
(2)∵△ABC 的周长为 14 cm,AC=6 cm,∴AB+BE+EC=8cm,即 2DE+2EC=8 cm.(8 分)∴ DC = DE + EC = 4 cm.(10分)
23.解:(1)如图.(3分)
(2)①②(6分)
(3)答案不唯一,如选择结论①BN 是∠ABC
的平分线.证明如下:∵AB=AC,∠A=36°,
∵MN 垂直平分AB,∴NA=NB.∴∠ABN=
∠A=36°.∴∠CBN=∠ABC-∠ABN=36°.
∴∠CBN=∠ABN.∴BN 是∠ABC 的平分
线.(10分)
24.(1) 证明:在等 边 △ABC 中,AB =AC,∠BAE=∠ACD=60°.△BAE≌△ACD
∴∠ABE = ∠CAD.∴∠BPQ =∠ABE + ∠BAP = ∠CAD + ∠BAP =∠BAC=60°.∵BQ⊥AD 于 Q,∴∠BQP=90°.∴∠PBQ=30°.∴BP=2PQ.(5分)
(2)解:∵∠ABE =∠CAD,∴∠ABC=∠ABE = ∠BAC- ∠CAD,即∠PBC =∠BAQ.∵△ABC 是等边三角形,∴AB=BC.∵BQ⊥AD,BP⊥PC,∴∠BQA =∠CPB = 90°. 在 △BAQ 和 △CBP 中,
.∴AQ=BP=2PQ.∴AP=PQ,即 (10)分)
25.解:(1)根据翻折可知∠AFE=∠DFE= ∵∠C=90°,∴∠CDF =90°—50°=40°.(3 分)
(2)∵△CDF 中,∠C=90°,且△CDF 是等腰 三 角 形, ∴CF= CD. ∴ ∠CFD =∠CDF=45°.连接 AD.设∠DAE=x.由对称性可知AF=FD,AE=DE,∴∠FDA= ∠CFD = 22.5°,∠ADE =∠DAE =x,∠DEB=2∠DAE=2x.(5分)
① 如 图 ①, 当 DE = DB 时,∠B =∠DEB=2x.由∠CDE=∠DEB+∠B,得 解得x=22.5°.此时∠B=2x=45°.(7分)
②如图②,当BD=BE时,则∠B=180°=4x.由∠CDE =∠DEB+∠B,得 解得x=37.5°.此时∠ .(9分)
③当 DE =BE 时,则 由∠CDE=∠DEB+∠B,得( 此方程无解.∴DE=BE 不成立.(11 分)综上所述,∠B =45°或 30°.(12分)
