综合滚动练习:等腰三角形的性质与判定 (含答案)2024—2025学年人教版数学八年级上册
文档属性
| 名称 | 综合滚动练习:等腰三角形的性质与判定 (含答案)2024—2025学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 356.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 06:32:07 | ||
图片预览

文档简介
综合滚动练习:等腰三角形的性质与判定
范围:13.3 满分:100分 时间:45分钟 得分:
一、选择题(每小题4 分,共32分)
1.在等腰△ABC中,∠A=120°,则底角的大小为( )
A.60° B.30°或 120°
C.120° D.30°
2.已知等腰三角形的一边长为8,一个内角为60°,则它的周长是 ( )
A.16 B.20 C.24 D.25
3.如图,在△ABC中,∠C=90°,∠BAC=60°,AD是角平分线.若 BD=8,则CD 的长为 ( )
A.4 B.3 C.2 D.1
4.如图,在 Rt△ABC 中,∠ACB=90°,∠A =50°,以点 B 为圆心,BC 长为半径画弧,交AB于点 D,连接CD,则∠ACD 的度数是 ( )
A.50° B.40° C.30° D.20°
5.如图,在钝角三角形ABC 中,∠ABC 为钝角,以点 B 为圆心,AB 长为半径画弧;再以点 C为圆心,AC长为半径画弧;两弧交于点 D,连接AD,CB 的延长线交AD 于点E.下列结论错误的是 ( )
A. CE 垂直平分AD
B. CE 平分∠ACD
C.△ABD 是等腰三角形
D.△ACD 是等边三角形
6.如图,在△ABC 中,∠BAC=110°,AB=AC,AD⊥BC 于点D,AB 的垂直平分线交 AB 于点E,交 BC 于点 F,连接AF,则∠FAD 的度数为( )
A.20° B.30° C.35° D.70°
7.如图,在△ABC中,∠BAC>90°,D 为 BC 的中点,点 E 在 AC上,将△CDE 沿 DE 折叠,使得点 C 恰好落在BA 的延长线上的点F 处,连接AD、CF,则图中所有的等腰三角形的个数为 ( )
A.1 B.2 C.3 D.4
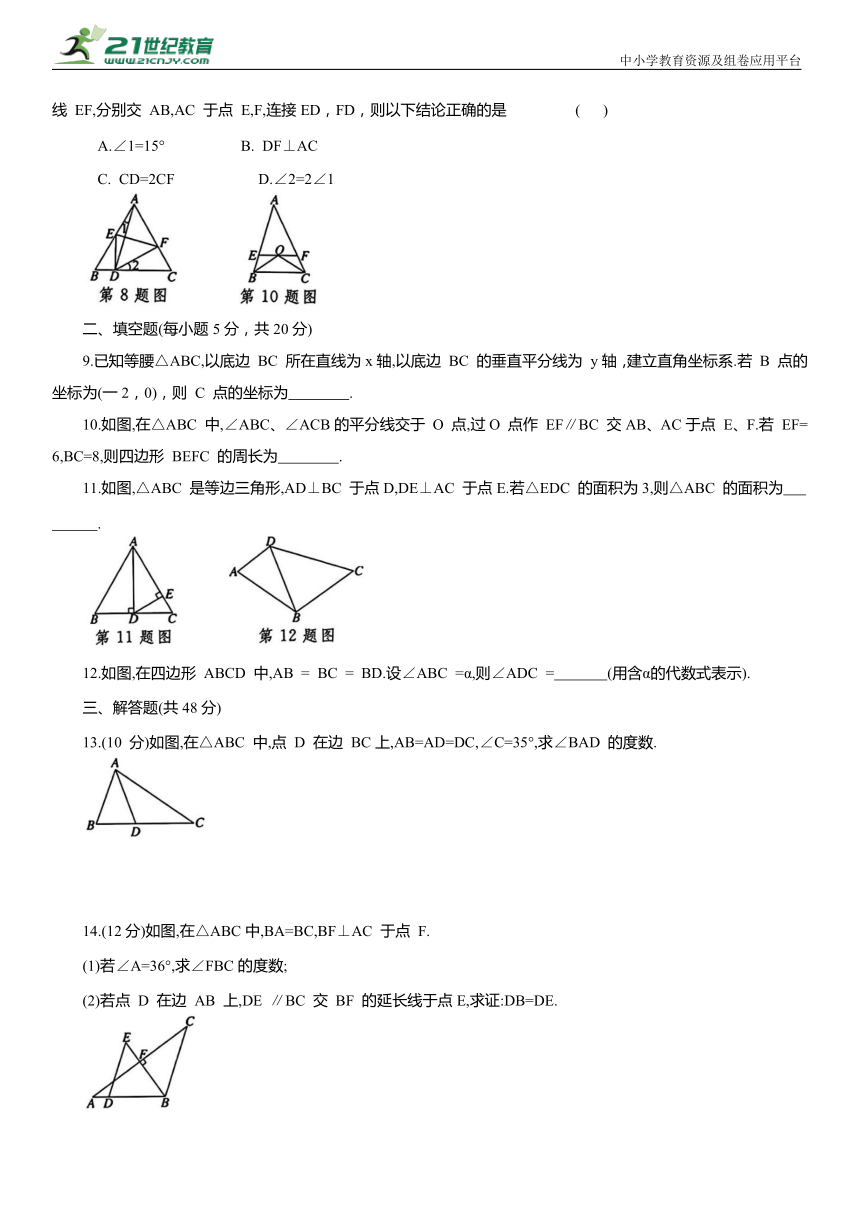
8.如图,在等边△ABC 中,点 D 是边 BC 上的一个动点(不与两端点重合),连接AD,作线段 AD 的垂直平分线 EF,分别交 AB,AC 于点 E,F,连接ED,FD,则以下结论正确的是 ( )
A.∠1=15° B. DF⊥AC
C. CD=2CF D.∠2=2∠1
二、填空题(每小题5分,共20分)
9.已知等腰△ABC,以底边 BC 所在直线为x轴,以底边 BC 的垂直平分线为 y轴,建立直角坐标系.若 B 点的坐标为(一2,0),则 C 点的坐标为 .
10.如图,在△ABC 中,∠ABC、∠ACB的平分线交于 O 点,过O 点作 EF∥BC 交AB、AC于点 E、F.若 EF=6,BC=8,则四边形 BEFC 的周长为 .
11.如图,△ABC 是等边三角形,AD⊥BC 于点D,DE⊥AC 于点E.若△EDC 的面积为3,则△ABC 的面积为 .
12.如图,在四边形 ABCD 中,AB = BC = BD.设∠ABC =α,则∠ADC = (用含α的代数式表示).
三、解答题(共48分)
13.(10 分)如图,在△ABC 中,点 D 在边 BC上,AB=AD=DC,∠C=35°,求∠BAD 的度数.
14.(12分)如图,在△ABC中,BA=BC,BF⊥AC 于点 F.
(1)若∠A=36°,求∠FBC的度数;
(2)若点 D 在边 AB 上,DE ∥BC 交 BF 的延长线于点E,求证:DB=DE.
15.(12分)如图,在等边△ABC 中,P 为AB 边上的一点,线段 BC 与 DC 关于直线CP 对称,连接 DA 并延长交直线CP 于点E.
(1)若∠ACE=20°,求∠CED的度数;
(2)若AE=1,CE=4,求 AD 的长.
16.(14分)如图,在平面直角坐标系中,△AOP为等边三角形,A(0,2),点 B 为y 轴上一动点,以 BP 为边作等边△BPC,延长CA 交x轴于点E.
(1)求证:OB=AC;
(2)当 B 点运动时,AE 的长度是否发生变化 并说明理由;
(3)在(2)的条件下,在y 轴上存在点Q,使得△AEQ 为等腰三角形.请直接写出 Q 的坐标: .
中小学教育资源及组卷应用平台
综合滚动练习:等腰三角形的性质与判定
1. D 5. D 6. A 4. D 2. C 3. A 4. D 8. D9.(2,0) 10.20 11.24 12.180°-a/2
13.解:∵AD = DC,∴∠DAC = ∠C = 35°.∴∠ADB=∠DAC+∠C =70°.∵AB =AD,∴∠B=∠ADB=70°.∴∠BAD= 40°.(10分)
14.(1)解:∵BA=BC,∴∠C=∠A=36°.∵ BF ⊥ AC 于 点 F, ∴ ∠BFC = 90°. (5分)
(2)证明:∵BA=BC,BF⊥AC 于点 F,∴∠ABF=∠FBC.∵DE∥BC,∴∠E=∠FBC.∴∠E = ∠ABF.∴DB= DE.(12分)
15.解: (1) ∵ △ABC 是 等 边 三 角 形,∴∠ACB=60°,CB=CA.∵∠ACE=20°, .由翻折的性质可知 CB=CD,∠ECB=∠ECD =40°.
∴ CA = CD,∠ACD = 40°= 20°= 20°.
∴∠CAD=∠D=80°.∵∠DAC=∠CED+∠ACE,∴∠CED=80°-20°=60°.(5分)
(2)过点 C 作 CT⊥DE 于 T.设∠ECA =α, 则 ∠ECB = ∠ECD = 60°— α, ∵∠DAC=∠E+∠ACE,∴∠E=60°+α-- α = 60°.∵CT⊥AD,CA = CD,∴AT= DT, ∠ECT = 30°. ∴ ET = EC=2.∴AT=ET-AE=2--1=1.∴AD=2AT=2.(12分)
16.(1)证明:∵△BPC 和△AOP 是等边三角形,∴OP = AP,BP = PC,∠APO =∠CPB = 60°. ∴ ∠APO + ∠APB =∠BPC+∠APB,即∠OPB=∠APC.在△PBO 和△PCA 中, ∴△PBO≌△PCA(SAS).∴OB = AC.(5分)
(2)解:当B 点运动时,AE 的长度不发生变化,理由是:由(1)知△PBO≌△PCA,∴∠BOP =60°.∴∠EAO=60°.∴∠EAO=60°.∵∠AOE =90°,∴∠AEO=30°.∵A(0,2),∴OA=2.∴AE=2AO=4.即AE 的长度不发生变化.(10分)
(3)(0,-2)或(0,6)(14分)
范围:13.3 满分:100分 时间:45分钟 得分:
一、选择题(每小题4 分,共32分)
1.在等腰△ABC中,∠A=120°,则底角的大小为( )
A.60° B.30°或 120°
C.120° D.30°
2.已知等腰三角形的一边长为8,一个内角为60°,则它的周长是 ( )
A.16 B.20 C.24 D.25
3.如图,在△ABC中,∠C=90°,∠BAC=60°,AD是角平分线.若 BD=8,则CD 的长为 ( )
A.4 B.3 C.2 D.1
4.如图,在 Rt△ABC 中,∠ACB=90°,∠A =50°,以点 B 为圆心,BC 长为半径画弧,交AB于点 D,连接CD,则∠ACD 的度数是 ( )
A.50° B.40° C.30° D.20°
5.如图,在钝角三角形ABC 中,∠ABC 为钝角,以点 B 为圆心,AB 长为半径画弧;再以点 C为圆心,AC长为半径画弧;两弧交于点 D,连接AD,CB 的延长线交AD 于点E.下列结论错误的是 ( )
A. CE 垂直平分AD
B. CE 平分∠ACD
C.△ABD 是等腰三角形
D.△ACD 是等边三角形
6.如图,在△ABC 中,∠BAC=110°,AB=AC,AD⊥BC 于点D,AB 的垂直平分线交 AB 于点E,交 BC 于点 F,连接AF,则∠FAD 的度数为( )
A.20° B.30° C.35° D.70°
7.如图,在△ABC中,∠BAC>90°,D 为 BC 的中点,点 E 在 AC上,将△CDE 沿 DE 折叠,使得点 C 恰好落在BA 的延长线上的点F 处,连接AD、CF,则图中所有的等腰三角形的个数为 ( )
A.1 B.2 C.3 D.4
8.如图,在等边△ABC 中,点 D 是边 BC 上的一个动点(不与两端点重合),连接AD,作线段 AD 的垂直平分线 EF,分别交 AB,AC 于点 E,F,连接ED,FD,则以下结论正确的是 ( )
A.∠1=15° B. DF⊥AC
C. CD=2CF D.∠2=2∠1
二、填空题(每小题5分,共20分)
9.已知等腰△ABC,以底边 BC 所在直线为x轴,以底边 BC 的垂直平分线为 y轴,建立直角坐标系.若 B 点的坐标为(一2,0),则 C 点的坐标为 .
10.如图,在△ABC 中,∠ABC、∠ACB的平分线交于 O 点,过O 点作 EF∥BC 交AB、AC于点 E、F.若 EF=6,BC=8,则四边形 BEFC 的周长为 .
11.如图,△ABC 是等边三角形,AD⊥BC 于点D,DE⊥AC 于点E.若△EDC 的面积为3,则△ABC 的面积为 .
12.如图,在四边形 ABCD 中,AB = BC = BD.设∠ABC =α,则∠ADC = (用含α的代数式表示).
三、解答题(共48分)
13.(10 分)如图,在△ABC 中,点 D 在边 BC上,AB=AD=DC,∠C=35°,求∠BAD 的度数.
14.(12分)如图,在△ABC中,BA=BC,BF⊥AC 于点 F.
(1)若∠A=36°,求∠FBC的度数;
(2)若点 D 在边 AB 上,DE ∥BC 交 BF 的延长线于点E,求证:DB=DE.
15.(12分)如图,在等边△ABC 中,P 为AB 边上的一点,线段 BC 与 DC 关于直线CP 对称,连接 DA 并延长交直线CP 于点E.
(1)若∠ACE=20°,求∠CED的度数;
(2)若AE=1,CE=4,求 AD 的长.
16.(14分)如图,在平面直角坐标系中,△AOP为等边三角形,A(0,2),点 B 为y 轴上一动点,以 BP 为边作等边△BPC,延长CA 交x轴于点E.
(1)求证:OB=AC;
(2)当 B 点运动时,AE 的长度是否发生变化 并说明理由;
(3)在(2)的条件下,在y 轴上存在点Q,使得△AEQ 为等腰三角形.请直接写出 Q 的坐标: .
中小学教育资源及组卷应用平台
综合滚动练习:等腰三角形的性质与判定
1. D 5. D 6. A 4. D 2. C 3. A 4. D 8. D9.(2,0) 10.20 11.24 12.180°-a/2
13.解:∵AD = DC,∴∠DAC = ∠C = 35°.∴∠ADB=∠DAC+∠C =70°.∵AB =AD,∴∠B=∠ADB=70°.∴∠BAD= 40°.(10分)
14.(1)解:∵BA=BC,∴∠C=∠A=36°.∵ BF ⊥ AC 于 点 F, ∴ ∠BFC = 90°. (5分)
(2)证明:∵BA=BC,BF⊥AC 于点 F,∴∠ABF=∠FBC.∵DE∥BC,∴∠E=∠FBC.∴∠E = ∠ABF.∴DB= DE.(12分)
15.解: (1) ∵ △ABC 是 等 边 三 角 形,∴∠ACB=60°,CB=CA.∵∠ACE=20°, .由翻折的性质可知 CB=CD,∠ECB=∠ECD =40°.
∴ CA = CD,∠ACD = 40°= 20°= 20°.
∴∠CAD=∠D=80°.∵∠DAC=∠CED+∠ACE,∴∠CED=80°-20°=60°.(5分)
(2)过点 C 作 CT⊥DE 于 T.设∠ECA =α, 则 ∠ECB = ∠ECD = 60°— α, ∵∠DAC=∠E+∠ACE,∴∠E=60°+α-- α = 60°.∵CT⊥AD,CA = CD,∴AT= DT, ∠ECT = 30°. ∴ ET = EC=2.∴AT=ET-AE=2--1=1.∴AD=2AT=2.(12分)
16.(1)证明:∵△BPC 和△AOP 是等边三角形,∴OP = AP,BP = PC,∠APO =∠CPB = 60°. ∴ ∠APO + ∠APB =∠BPC+∠APB,即∠OPB=∠APC.在△PBO 和△PCA 中, ∴△PBO≌△PCA(SAS).∴OB = AC.(5分)
(2)解:当B 点运动时,AE 的长度不发生变化,理由是:由(1)知△PBO≌△PCA,∴∠BOP =60°.∴∠EAO=60°.∴∠EAO=60°.∵∠AOE =90°,∴∠AEO=30°.∵A(0,2),∴OA=2.∴AE=2AO=4.即AE 的长度不发生变化.(10分)
(3)(0,-2)或(0,6)(14分)
