解题技巧专题:利用等腰三角形的“三线合一”作辅助线(含答案)
文档属性
| 名称 | 解题技巧专题:利用等腰三角形的“三线合一”作辅助线(含答案) | 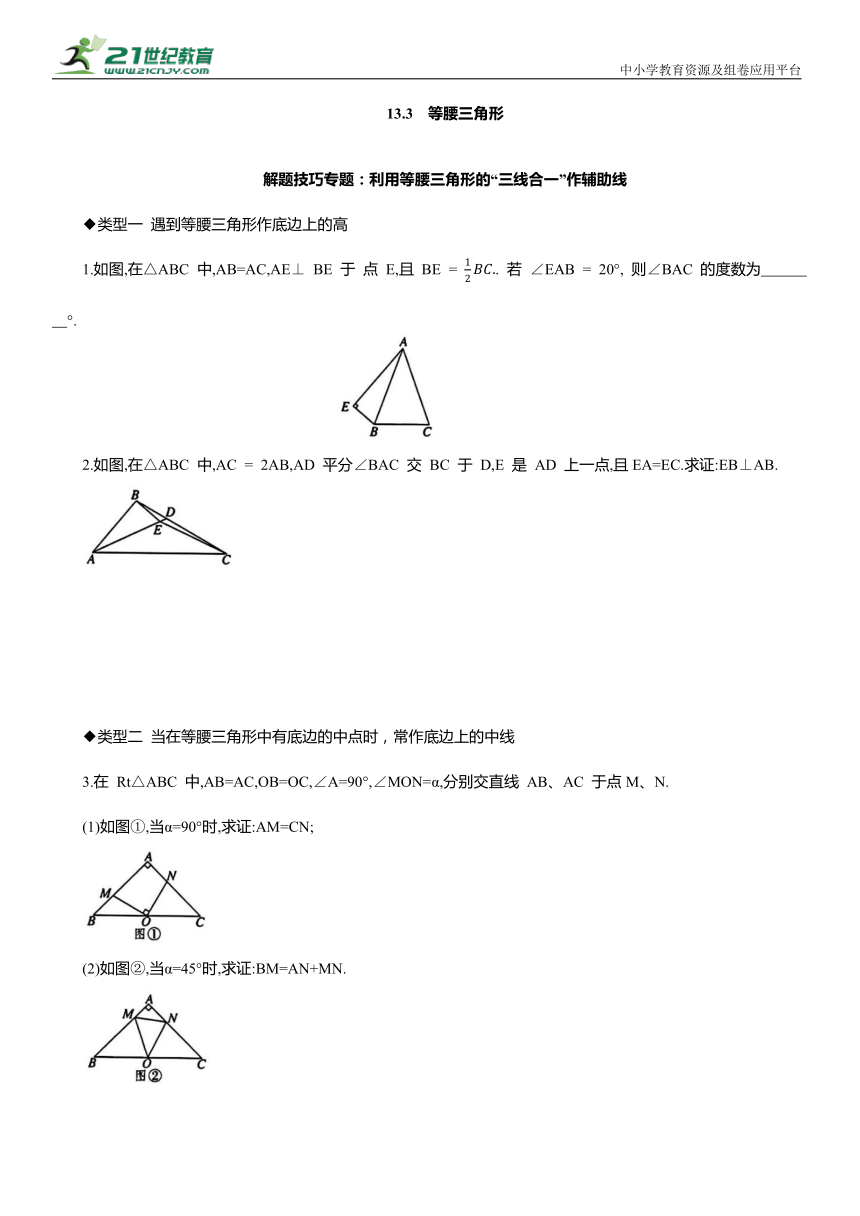 | |
| 格式 | docx | ||
| 文件大小 | 195.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 06:44:02 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
13.3 等腰三角形
解题技巧专题:利用等腰三角形的“三线合一”作辅助线
◆类型一 遇到等腰三角形作底边上的高
1.如图,在△ABC 中,AB=AC,AE⊥ BE 于 点 E,且 BE = . 若 ∠EAB = 20°, 则∠BAC 的度数为 °.
2.如图,在△ABC 中,AC = 2AB,AD 平分∠BAC 交 BC 于 D,E 是 AD 上一点,且EA=EC.求证:EB⊥AB.
◆类型二 当在等腰三角形中有底边的中点时,常作底边上的中线
3.在 Rt△ABC 中,AB=AC,OB=OC,∠A=90°,∠MON=α,分别交直线 AB、AC 于点M、N.
(1)如图①,当α=90°时,求证:AM=CN;
(2)如图②,当α=45°时,求证:BM=AN+MN.
类型三 当遇到与角平分线垂直的线段时,可构造等腰三角形
4.如图,在△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为 D,AD 与 BC交于点 E.求证:AE=2CD.
解题技巧专题:利用等腰三角形的“三线合一”作辅助线
1.40
2.证明:作 EF⊥AC 于 F.∵EA=EC,∴AF=FC= AC.∵AC=2AB,∴AF=AB.∵AD平分∠BAC,∴∠BAD=∠CAD.在△BAE 和△FAE 中,△FAE (SAS). ∴ ∠ABE = ∠AFE = 90°.∴EB⊥AB.
3.证明:(1)如图①,连接 OA.∵AB=AC,∠BAC = 90°, OB = OC, ∴ AO ⊥ BC,∠ABO=∠ACO=∠BAO=∠CAO=45°,OA=OB=OC.∴∠MON=∠AOC=90°.∴∠AOM=∠CON.又AO=CO,∠BAO=∠ACO=45°,∴△AOM≌△CON(ASA).∴AM=CN.
(2)如图②,在 BA 上截取BG=AN,连接GO,AO.∵AB=AC,∠BAC=90°,OB =OC,∴AO⊥BC,OA=OB=OC,∠ABO=∠ACO =∠BAO =∠CAO = 45°.∵BG=AN,∠ABO=∠NAO = 45°,AO = BO,∴△BGO≌△ANO(SAS).∴OG =ON,∠BOG = ∠AON. ∵ ∠MON = 45°=∠AOM+∠AON,∴∠AOM+∠BOG =45°.∵∠AOB=90°,∴∠MOG=∠MON=45°.∵MO = MO,GO= NO,∴△GMO≌△NMO(SAS).∴GM=MN.∴BM=BG+GM=AN+MN.
4.证明:延长 AB、CD 交于点 G.∵AD 平分∠BAC,∴∠CAD =∠GAD.∵AD⊥CD,∴ ∠ADC = ∠ADG= 90°. 在 △ADC 和△ADG 中,10000.00.00∴△ADC≌△ADG(ASA).∴CD=GD,即CG=2CD.易得∠BAE=∠ECD.又∠ABE=∠CBG=90°,AB=BC,∴△ABE≌△CBG(ASA).∴AE=CG=2CD.
13.3 等腰三角形
解题技巧专题:利用等腰三角形的“三线合一”作辅助线
◆类型一 遇到等腰三角形作底边上的高
1.如图,在△ABC 中,AB=AC,AE⊥ BE 于 点 E,且 BE = . 若 ∠EAB = 20°, 则∠BAC 的度数为 °.
2.如图,在△ABC 中,AC = 2AB,AD 平分∠BAC 交 BC 于 D,E 是 AD 上一点,且EA=EC.求证:EB⊥AB.
◆类型二 当在等腰三角形中有底边的中点时,常作底边上的中线
3.在 Rt△ABC 中,AB=AC,OB=OC,∠A=90°,∠MON=α,分别交直线 AB、AC 于点M、N.
(1)如图①,当α=90°时,求证:AM=CN;
(2)如图②,当α=45°时,求证:BM=AN+MN.
类型三 当遇到与角平分线垂直的线段时,可构造等腰三角形
4.如图,在△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为 D,AD 与 BC交于点 E.求证:AE=2CD.
解题技巧专题:利用等腰三角形的“三线合一”作辅助线
1.40
2.证明:作 EF⊥AC 于 F.∵EA=EC,∴AF=FC= AC.∵AC=2AB,∴AF=AB.∵AD平分∠BAC,∴∠BAD=∠CAD.在△BAE 和△FAE 中,△FAE (SAS). ∴ ∠ABE = ∠AFE = 90°.∴EB⊥AB.
3.证明:(1)如图①,连接 OA.∵AB=AC,∠BAC = 90°, OB = OC, ∴ AO ⊥ BC,∠ABO=∠ACO=∠BAO=∠CAO=45°,OA=OB=OC.∴∠MON=∠AOC=90°.∴∠AOM=∠CON.又AO=CO,∠BAO=∠ACO=45°,∴△AOM≌△CON(ASA).∴AM=CN.
(2)如图②,在 BA 上截取BG=AN,连接GO,AO.∵AB=AC,∠BAC=90°,OB =OC,∴AO⊥BC,OA=OB=OC,∠ABO=∠ACO =∠BAO =∠CAO = 45°.∵BG=AN,∠ABO=∠NAO = 45°,AO = BO,∴△BGO≌△ANO(SAS).∴OG =ON,∠BOG = ∠AON. ∵ ∠MON = 45°=∠AOM+∠AON,∴∠AOM+∠BOG =45°.∵∠AOB=90°,∴∠MOG=∠MON=45°.∵MO = MO,GO= NO,∴△GMO≌△NMO(SAS).∴GM=MN.∴BM=BG+GM=AN+MN.
4.证明:延长 AB、CD 交于点 G.∵AD 平分∠BAC,∴∠CAD =∠GAD.∵AD⊥CD,∴ ∠ADC = ∠ADG= 90°. 在 △ADC 和△ADG 中,10000.00.00∴△ADC≌△ADG(ASA).∴CD=GD,即CG=2CD.易得∠BAE=∠ECD.又∠ABE=∠CBG=90°,AB=BC,∴△ABE≌△CBG(ASA).∴AE=CG=2CD.
