13.4 课题学习 最短路径问题 同步练习(含答案) 2024—2025学年人教版数学八年级上册
文档属性
| 名称 | 13.4 课题学习 最短路径问题 同步练习(含答案) 2024—2025学年人教版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 943.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 00:00:00 | ||
图片预览




文档简介
13.4 课题学习 最短路径问题
A层
知识点一 最短路径问题
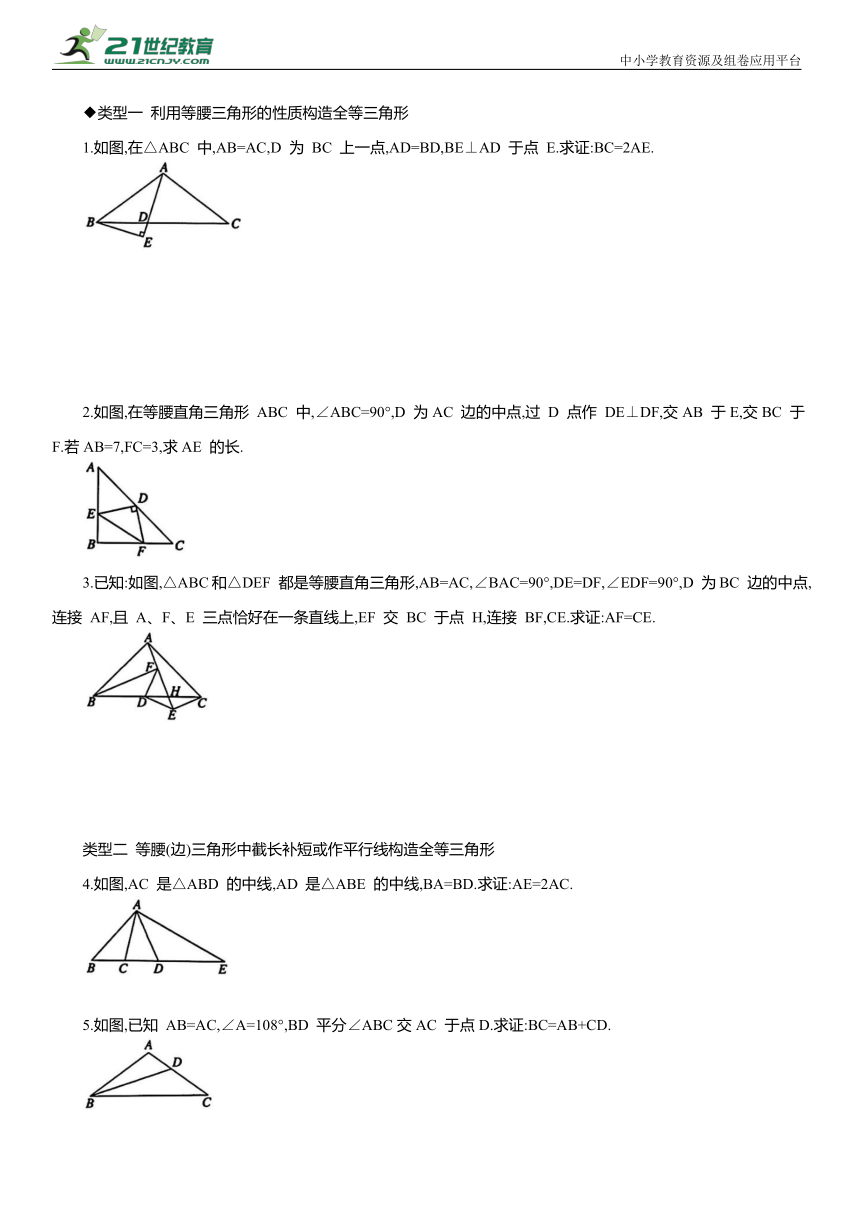
1.已知点 A、点 B 都在直线l 的上方,试用尺规作图在直线 l 上求作一点 P,使得 PA+PB的值最小,则下列作法正确的是 ( )
2.如图,在正方形网格中有 M,N 两点,在直线l上求一点P 使PM+PN 最短,则点 P 应选在( )
A. A 点 B. B 点 C. C 点 D. D 点
3.如图,在△ABC 中,AB=3,AC=4,EF 垂直平分BC,点 P 为直线EF 上的任意一点,则AP+BP 的最小值是 ( )
A.4 B.5 C.6 D.7
4.如图,某牧童在 A 处放牛,其家在 B 处,A、B到河岸的距离分别为AC、BD,且 AC=BD,若 A 到河岸CD 的中点的距离为 500米.
(1)牧童从 A 处把牛牵到河边饮水后再回家,试问在何处饮水所走的路程最短
(2)最短路程是多少
5.作图题:线段 AC 是正方形ABCD 的对角线,点 M 是边CD 上的一定点(不与 D、C 重合),请在对角线 AC 上找一点 P,使得△PDM 的周长最小,并作简要说明.
知识点二 造桥选址问题
6.A 和B 两地在一条河的两岸,现要在河上造一座桥 MN,使从 A 到B 的路径AMNB 最短的是(假定河的两岸是平行线,桥与河岸垂直)( )
B层
7.如图,MN 是等边三角形ABC 的一条对称轴,D 为AC 的中点,点 P 是直线MN 上的一个动点,当 PC+PD 的值最小时,∠PCD 的度数是 ( )
A.30°
B.15°
C.20°
D.35°
8.如图,△ABC 的面积为16,AB=AC,BC=4,AC 的垂直平分线 EF 分别交 AB,AC 边于点E,F.若点 D 为 BC边的中点,点 P 为线段 EF上一动点,则△PCD 周长的最小值为 .
9.如图,正三角形 ABC 的边长为6,过点 B 的直线l⊥AB,且△ABC 与△A'BC'关于直线l对称,D 为线段BC'上一动点,则AD+CD 的最小值是 .
10.如图,在由边长为1个单位长度的小正方形组成的网格中,请分别在边 AB,AC 上找到点E,F,使四边形 PEFQ 的周长最小.
11.某班级在探究“将军饮马问题”时抽象出数学模型:
直线 l 同旁有两个定点A、B,在直线l 上存在点P,使得 PA+PB 的值最小.
解法:如图①,作点 A 关于直线l的对称点A',连接A'B,则A'B 与直线l 的交点即为P,且 PA+PB 的最小值为A'B.请利用上述模型解决下列问题.
(1)如图②,△ABC 中,∠C=90°,E 是 AB的中点,P 是 BC 边上的一动点,作出点P,使得 PA+PE 的值最小;
(2)如图③,∠AOB=30°,M、N 分别为OA、OB 上一动点,若 OP=5,求△PMN 的周长的最小值.
中小学教育资源及组卷应用平台
解题技巧专题:巧用等腰三角形构造全等三角形解题
◆类型一 利用等腰三角形的性质构造全等三角形
1.如图,在△ABC 中,AB=AC,D 为 BC 上一点,AD=BD,BE⊥AD 于点 E.求证:BC=2AE.
2.如图,在等腰直角三角形 ABC 中,∠ABC=90°,D 为AC 边的中点,过 D 点作 DE⊥DF,交AB 于E,交BC 于F.若AB=7,FC=3,求AE 的长.
3.已知:如图,△ABC和△DEF 都是等腰直角三角形,AB=AC,∠BAC=90°,DE=DF,∠EDF=90°,D 为BC 边的中点,连接 AF,且 A、F、E 三点恰好在一条直线上,EF 交 BC 于点 H,连接 BF,CE.求证:AF=CE.
类型二 等腰(边)三角形中截长补短或作平行线构造全等三角形
4.如图,AC 是△ABD 的中线,AD 是△ABE 的中线,BA=BD.求证:AE=2AC.
5.如图,已知 AB=AC,∠A=108°,BD 平分∠ABC交AC 于点D.求证:BC=AB+CD.
6.如图,过等边△ABC 的边AB 上一点 P,作PE⊥AC 于 E,Q 为 BC 延长线上一点,且PA=CQ,连接 PQ交 AC边于 D.
(1)求证:PD=DQ;
(2)若△ABC 的边长为1,求 DE 的长.
类型三 在直角坐标系中利用等腰三角形构造全等三角形求点的坐标
7.如图,在△ABC中,AB=BC,AB⊥BC,B(0,2),C(2,-2),求点 A 的坐标.
8.已知A(-10,0),以OA 为边在第二象限作等边△AOB.
(1)求点 B 的横坐标;
(2)如图,点 M、N 分别为OB、OA 边上的动点,以 MN 为 边 在 x 轴上 方 作 等 边△MNE,连接OE,当∠EMO=45°时,求∠MEO 的度数.
13.4 课题学习 最短路径问题
1. D 2. C 3. A
4.解:(1)在CD 的中点处饮水所走的路程最短.
(2)最短路程是 1000 米.
5.解:如图,连接BM,交AC 于点P,点 P 即为所求.
6. D 7. A 8.10 9.12
10.解:如图,分别作 P 关于AB,Q关于AC 的对称点P',Q',连接 P'Q',交 AB 于 E,交AC 于 F,则 E,F 即为所求.
11.解:(1)作点 A 关于直线 BC 的对称点 A ,连接A E,交 BC 于点P,如图②所示,点 P即为所求.
(2)作点 P 关于直线 OA 的对称点 F,作点
P 关于直线OB 的对称点G,连接 FG,分别
交OA、OB 于 M、N,如图③.根据“将军饮
马问题”得到△PMN 的周长的最小值为
FG.由轴对称的性质得∠FOA=∠AOP,
∠POB = ∠GOB,OP = OF,OP = OG.
∵∠AOP+∠POB=∠AOB=30°,OP=
5, ∴ ∠FOG = ∠FOA + ∠AOP +
∠POB + ∠GOB = 60°, OF = OG = 5.
∴△FOG 是 边 长 为 5 的 等 边 三 角 形.
∴FG=5.∴△PMN 的周长的最小值为5.
解题技巧专题:巧用等腰三角形构造全等三角形解题
1.证明:如图,过 A 作 AN⊥BC 于 N,则 BN=CN.∵AD=BD,∴∠DAB=∠DBA.∵BE⊥AD,∴∠E =∠ANB = 90°.在△ABN 与△BAE 中,
△BAE(AAS).∴BN=AE.∴BC=2BN=2AE.
2. 解: 如 图, 连 接 BD.∵∠ABC=90°,AB=CB,∴∠A=∠C=45°.∵D 为AC 边的 中点, ∠4,∠ADB = 90°.∴ ∠1 + ∠2 = 90°.∵DE⊥DF,∴∠EDF=90°.∴∠2+∠3=90°.∴∠1=∠3.在△ADE 和△BDF 中,
∴AE=BF.∵AB=7,∴BC=7.∵BF=BC--FC=4,∴AE=4.
3.证 明: 如图, 连 接 AD.∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°.∵ 点 D 为 BC 的 中 点, ∴∠DAC= 且 AD⊥BC.∴∠ADC=90°,且∠DAC =∠ACB.∴AD= CD.又∵∠EDF = 90°,∴∠ADC - ∠FDH =∠EDF--∠FDH,即∠ADF=∠CDE.在△AFD 和△CED中 ∴△AFD≌△CED(SAS).∴AF=CE.
4.证明:延长 AC 到点 F,使AC=CF,连接DF,如 图 所 示. ∵ AC 是△ABD 的 中 线,∴BC=DC.∵∠ACB=∠FCD,∴△ABC≌△FDC(SAS).∴∠B=∠FDC,DF=BA.又∵ BA = BD, AD 是 △ABE 的 中 线,∴∠BAD=∠BDA,DF=DE.∴∠ADE=∠B + ∠BAD = ∠FDC + ∠BDA =∠ADF.∵AD=AD,∴△ADE≌△ADF(SAS).∴AE=AF=2AC.
5.证明:如图,在线段 BC 上截取BE=BA,连接 DE.∵ BD 平 分 ∠ABC, C 在△ABD和△EBD中 △EBD(SAS).∴∠BED = ∠A = 108°,∠ADB=∠EDB.又∵AB = AC,∠A = 108°) = 36°.∴∠CDE =∠DEB --∠C =108°--36°=72°,∠DEC=180°--∠DEB=180°— 108°= 72°. ∴∠CDE = ∠DEC.∴CD=CE.∴BC=BE+EC=AB+CD.
6.(1)思路分析:
证明:如图,过 P 作PF∥BC交AC 于点 F,
∴∠AFP = ∠ACB,∠FPD=∠Q,∠PFD=∠QCD.∵△ABC 为等边三角形,∴∠A=∠ACB=60°.∴∠AFP=60°.∴△APF 是等边三角形.∴AP=PF.∵AP=CQ,∴PF=CQ.∴△PFD≌△QCD(ASA).∴PD=DQ.
(2)解:∵△APF 是等边三角形,PE⊥AC, 由(1)知△PFD≌ 又∵AC =1,
7.解:作 CM⊥y 轴于 M.∵B(0,2),C(2,-2),∴OM=2,CM=BO=2.∴BM=OM+BO=4.在 Rt△AOB 和 Rt△BMC 中,[DO-CN,∴Rt△AOB≌Rt△BMC(HL).∴AO=BM=4.∴A(-4,0).
8.解:(1)如图①,过 B 作 BD⊥OA 于点 D.∵△AOB为等边三角形,点 A(--10,0),∴OA=OB=AB=10,∠BAO=∠ABO=∠AOB=60°.∵BD⊥OA,∴AD=OD = 点 B 的横坐标为-5.
(2)如图②,过点 M 作MF∥AB 交OA 于点F, 则∠MFO = ∠BAO = ∠AOB = 60°.
∴△MOF为等边三角形.∴∠FMO=60°,MF = MO. ∵ △MNE 是 等 边 三 角 形,∴∠NME=60°,MN = ME.∴∠FMN+∠NMO = ∠NMO + ∠OME = 60°.
∴∠FMN=∠OME. △MFN ≌△MOE(SAS).∴∠MFN=∠MOE=60°.∵∠EMO=45°,∴∠MEO =180°—∠MOE —∠EMO =
A层
知识点一 最短路径问题
1.已知点 A、点 B 都在直线l 的上方,试用尺规作图在直线 l 上求作一点 P,使得 PA+PB的值最小,则下列作法正确的是 ( )
2.如图,在正方形网格中有 M,N 两点,在直线l上求一点P 使PM+PN 最短,则点 P 应选在( )
A. A 点 B. B 点 C. C 点 D. D 点
3.如图,在△ABC 中,AB=3,AC=4,EF 垂直平分BC,点 P 为直线EF 上的任意一点,则AP+BP 的最小值是 ( )
A.4 B.5 C.6 D.7
4.如图,某牧童在 A 处放牛,其家在 B 处,A、B到河岸的距离分别为AC、BD,且 AC=BD,若 A 到河岸CD 的中点的距离为 500米.
(1)牧童从 A 处把牛牵到河边饮水后再回家,试问在何处饮水所走的路程最短
(2)最短路程是多少
5.作图题:线段 AC 是正方形ABCD 的对角线,点 M 是边CD 上的一定点(不与 D、C 重合),请在对角线 AC 上找一点 P,使得△PDM 的周长最小,并作简要说明.
知识点二 造桥选址问题
6.A 和B 两地在一条河的两岸,现要在河上造一座桥 MN,使从 A 到B 的路径AMNB 最短的是(假定河的两岸是平行线,桥与河岸垂直)( )
B层
7.如图,MN 是等边三角形ABC 的一条对称轴,D 为AC 的中点,点 P 是直线MN 上的一个动点,当 PC+PD 的值最小时,∠PCD 的度数是 ( )
A.30°
B.15°
C.20°
D.35°
8.如图,△ABC 的面积为16,AB=AC,BC=4,AC 的垂直平分线 EF 分别交 AB,AC 边于点E,F.若点 D 为 BC边的中点,点 P 为线段 EF上一动点,则△PCD 周长的最小值为 .
9.如图,正三角形 ABC 的边长为6,过点 B 的直线l⊥AB,且△ABC 与△A'BC'关于直线l对称,D 为线段BC'上一动点,则AD+CD 的最小值是 .
10.如图,在由边长为1个单位长度的小正方形组成的网格中,请分别在边 AB,AC 上找到点E,F,使四边形 PEFQ 的周长最小.
11.某班级在探究“将军饮马问题”时抽象出数学模型:
直线 l 同旁有两个定点A、B,在直线l 上存在点P,使得 PA+PB 的值最小.
解法:如图①,作点 A 关于直线l的对称点A',连接A'B,则A'B 与直线l 的交点即为P,且 PA+PB 的最小值为A'B.请利用上述模型解决下列问题.
(1)如图②,△ABC 中,∠C=90°,E 是 AB的中点,P 是 BC 边上的一动点,作出点P,使得 PA+PE 的值最小;
(2)如图③,∠AOB=30°,M、N 分别为OA、OB 上一动点,若 OP=5,求△PMN 的周长的最小值.
中小学教育资源及组卷应用平台
解题技巧专题:巧用等腰三角形构造全等三角形解题
◆类型一 利用等腰三角形的性质构造全等三角形
1.如图,在△ABC 中,AB=AC,D 为 BC 上一点,AD=BD,BE⊥AD 于点 E.求证:BC=2AE.
2.如图,在等腰直角三角形 ABC 中,∠ABC=90°,D 为AC 边的中点,过 D 点作 DE⊥DF,交AB 于E,交BC 于F.若AB=7,FC=3,求AE 的长.
3.已知:如图,△ABC和△DEF 都是等腰直角三角形,AB=AC,∠BAC=90°,DE=DF,∠EDF=90°,D 为BC 边的中点,连接 AF,且 A、F、E 三点恰好在一条直线上,EF 交 BC 于点 H,连接 BF,CE.求证:AF=CE.
类型二 等腰(边)三角形中截长补短或作平行线构造全等三角形
4.如图,AC 是△ABD 的中线,AD 是△ABE 的中线,BA=BD.求证:AE=2AC.
5.如图,已知 AB=AC,∠A=108°,BD 平分∠ABC交AC 于点D.求证:BC=AB+CD.
6.如图,过等边△ABC 的边AB 上一点 P,作PE⊥AC 于 E,Q 为 BC 延长线上一点,且PA=CQ,连接 PQ交 AC边于 D.
(1)求证:PD=DQ;
(2)若△ABC 的边长为1,求 DE 的长.
类型三 在直角坐标系中利用等腰三角形构造全等三角形求点的坐标
7.如图,在△ABC中,AB=BC,AB⊥BC,B(0,2),C(2,-2),求点 A 的坐标.
8.已知A(-10,0),以OA 为边在第二象限作等边△AOB.
(1)求点 B 的横坐标;
(2)如图,点 M、N 分别为OB、OA 边上的动点,以 MN 为 边 在 x 轴上 方 作 等 边△MNE,连接OE,当∠EMO=45°时,求∠MEO 的度数.
13.4 课题学习 最短路径问题
1. D 2. C 3. A
4.解:(1)在CD 的中点处饮水所走的路程最短.
(2)最短路程是 1000 米.
5.解:如图,连接BM,交AC 于点P,点 P 即为所求.
6. D 7. A 8.10 9.12
10.解:如图,分别作 P 关于AB,Q关于AC 的对称点P',Q',连接 P'Q',交 AB 于 E,交AC 于 F,则 E,F 即为所求.
11.解:(1)作点 A 关于直线 BC 的对称点 A ,连接A E,交 BC 于点P,如图②所示,点 P即为所求.
(2)作点 P 关于直线 OA 的对称点 F,作点
P 关于直线OB 的对称点G,连接 FG,分别
交OA、OB 于 M、N,如图③.根据“将军饮
马问题”得到△PMN 的周长的最小值为
FG.由轴对称的性质得∠FOA=∠AOP,
∠POB = ∠GOB,OP = OF,OP = OG.
∵∠AOP+∠POB=∠AOB=30°,OP=
5, ∴ ∠FOG = ∠FOA + ∠AOP +
∠POB + ∠GOB = 60°, OF = OG = 5.
∴△FOG 是 边 长 为 5 的 等 边 三 角 形.
∴FG=5.∴△PMN 的周长的最小值为5.
解题技巧专题:巧用等腰三角形构造全等三角形解题
1.证明:如图,过 A 作 AN⊥BC 于 N,则 BN=CN.∵AD=BD,∴∠DAB=∠DBA.∵BE⊥AD,∴∠E =∠ANB = 90°.在△ABN 与△BAE 中,
△BAE(AAS).∴BN=AE.∴BC=2BN=2AE.
2. 解: 如 图, 连 接 BD.∵∠ABC=90°,AB=CB,∴∠A=∠C=45°.∵D 为AC 边的 中点, ∠4,∠ADB = 90°.∴ ∠1 + ∠2 = 90°.∵DE⊥DF,∴∠EDF=90°.∴∠2+∠3=90°.∴∠1=∠3.在△ADE 和△BDF 中,
∴AE=BF.∵AB=7,∴BC=7.∵BF=BC--FC=4,∴AE=4.
3.证 明: 如图, 连 接 AD.∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°.∵ 点 D 为 BC 的 中 点, ∴∠DAC= 且 AD⊥BC.∴∠ADC=90°,且∠DAC =∠ACB.∴AD= CD.又∵∠EDF = 90°,∴∠ADC - ∠FDH =∠EDF--∠FDH,即∠ADF=∠CDE.在△AFD 和△CED中 ∴△AFD≌△CED(SAS).∴AF=CE.
4.证明:延长 AC 到点 F,使AC=CF,连接DF,如 图 所 示. ∵ AC 是△ABD 的 中 线,∴BC=DC.∵∠ACB=∠FCD,∴△ABC≌△FDC(SAS).∴∠B=∠FDC,DF=BA.又∵ BA = BD, AD 是 △ABE 的 中 线,∴∠BAD=∠BDA,DF=DE.∴∠ADE=∠B + ∠BAD = ∠FDC + ∠BDA =∠ADF.∵AD=AD,∴△ADE≌△ADF(SAS).∴AE=AF=2AC.
5.证明:如图,在线段 BC 上截取BE=BA,连接 DE.∵ BD 平 分 ∠ABC, C 在△ABD和△EBD中 △EBD(SAS).∴∠BED = ∠A = 108°,∠ADB=∠EDB.又∵AB = AC,∠A = 108°) = 36°.∴∠CDE =∠DEB --∠C =108°--36°=72°,∠DEC=180°--∠DEB=180°— 108°= 72°. ∴∠CDE = ∠DEC.∴CD=CE.∴BC=BE+EC=AB+CD.
6.(1)思路分析:
证明:如图,过 P 作PF∥BC交AC 于点 F,
∴∠AFP = ∠ACB,∠FPD=∠Q,∠PFD=∠QCD.∵△ABC 为等边三角形,∴∠A=∠ACB=60°.∴∠AFP=60°.∴△APF 是等边三角形.∴AP=PF.∵AP=CQ,∴PF=CQ.∴△PFD≌△QCD(ASA).∴PD=DQ.
(2)解:∵△APF 是等边三角形,PE⊥AC, 由(1)知△PFD≌ 又∵AC =1,
7.解:作 CM⊥y 轴于 M.∵B(0,2),C(2,-2),∴OM=2,CM=BO=2.∴BM=OM+BO=4.在 Rt△AOB 和 Rt△BMC 中,[DO-CN,∴Rt△AOB≌Rt△BMC(HL).∴AO=BM=4.∴A(-4,0).
8.解:(1)如图①,过 B 作 BD⊥OA 于点 D.∵△AOB为等边三角形,点 A(--10,0),∴OA=OB=AB=10,∠BAO=∠ABO=∠AOB=60°.∵BD⊥OA,∴AD=OD = 点 B 的横坐标为-5.
(2)如图②,过点 M 作MF∥AB 交OA 于点F, 则∠MFO = ∠BAO = ∠AOB = 60°.
∴△MOF为等边三角形.∴∠FMO=60°,MF = MO. ∵ △MNE 是 等 边 三 角 形,∴∠NME=60°,MN = ME.∴∠FMN+∠NMO = ∠NMO + ∠OME = 60°.
∴∠FMN=∠OME. △MFN ≌△MOE(SAS).∴∠MFN=∠MOE=60°.∵∠EMO=45°,∴∠MEO =180°—∠MOE —∠EMO =
