13.3.2 等边三角形 同步练习 (含答案)2024—2025学年人教版数学八年级上册
文档属性
| 名称 | 13.3.2 等边三角形 同步练习 (含答案)2024—2025学年人教版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 881.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 06:38:16 | ||
图片预览


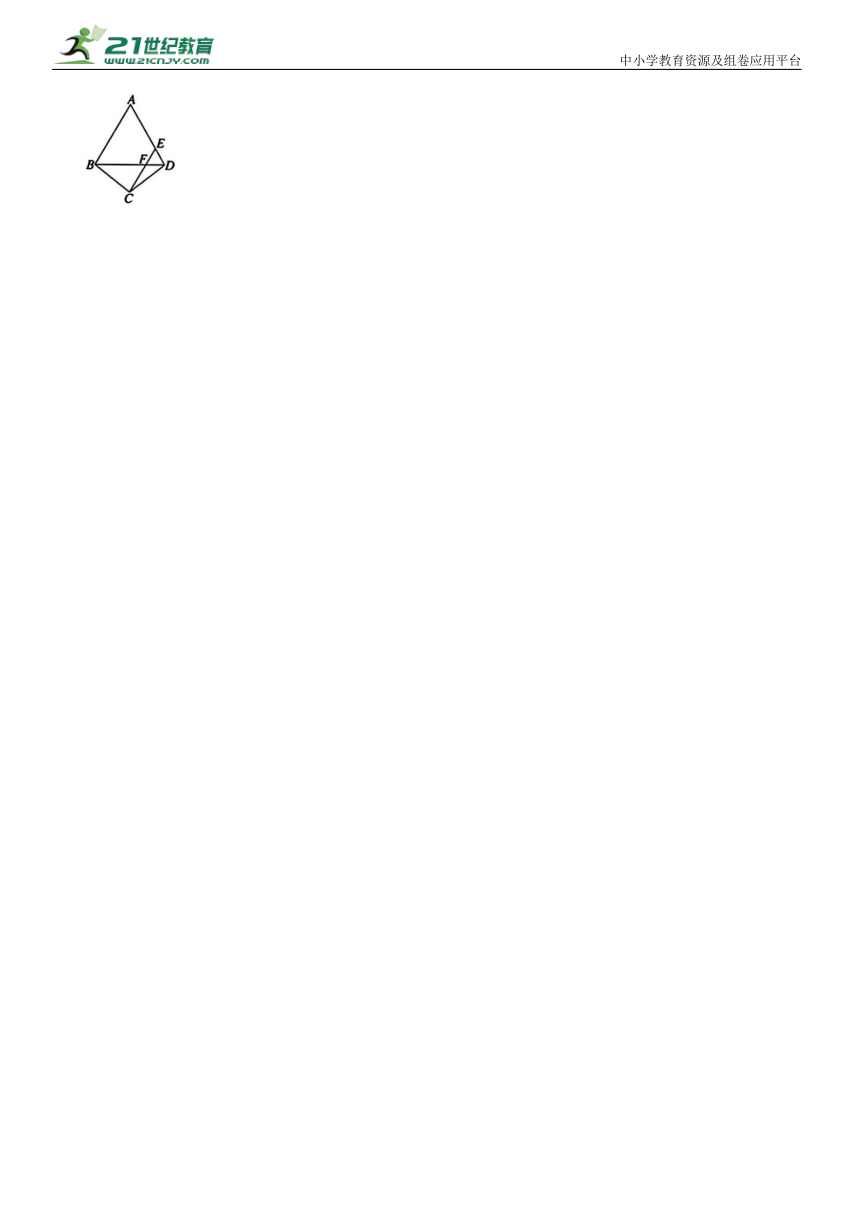


文档简介
13.3.2 等边三角形
第 1 课时 等边三角形的性质与判定
A层
知识点一 等边三角形的性质
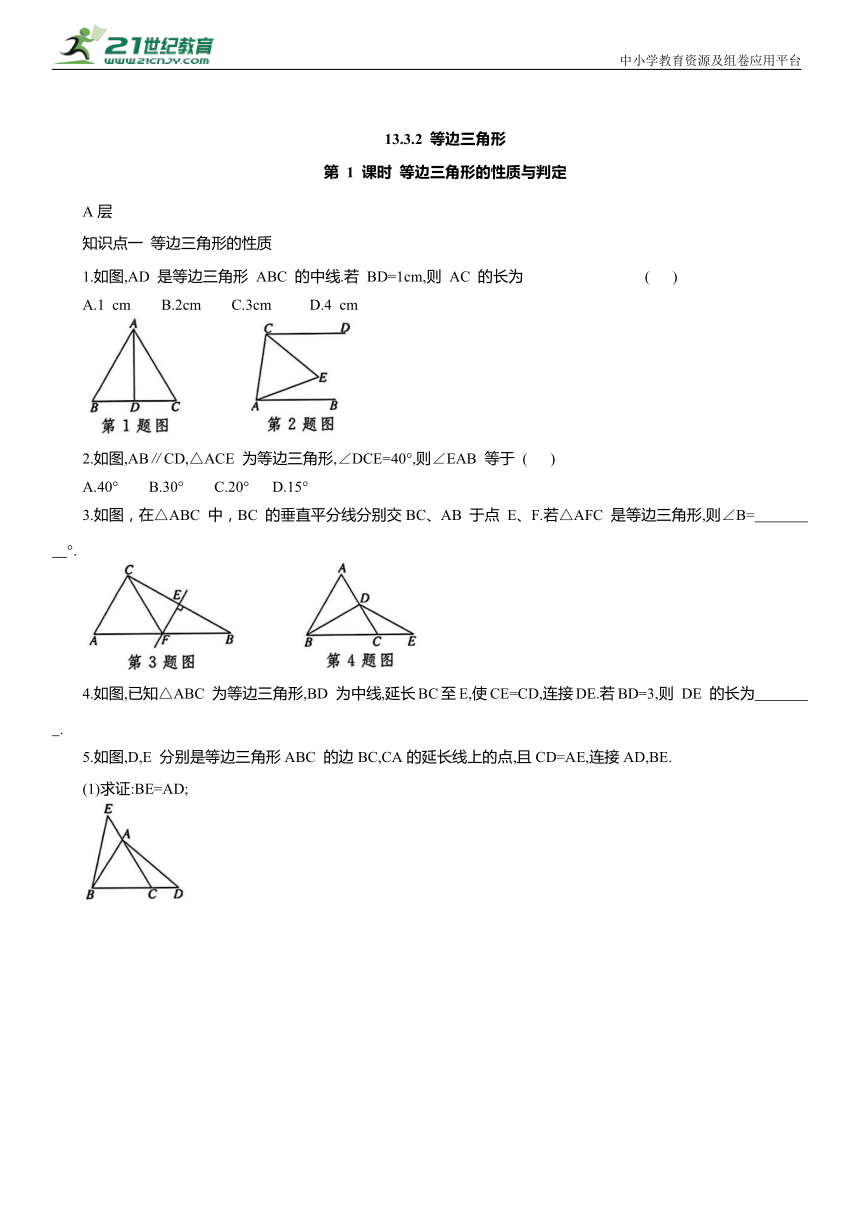
1.如图,AD 是等边三角形 ABC 的中线.若 BD=1cm,则 AC 的长为 ( )
A.1 cm B.2cm C.3cm D.4 cm
2.如图,AB∥CD,△ACE 为等边三角形,∠DCE=40°,则∠EAB 等于 ( )
A.40° B.30° C.20° D.15°
3.如图,在△ABC 中,BC 的垂直平分线分别交BC、AB 于点 E、F.若△AFC 是等边三角形,则∠B= °.
4.如图,已知△ABC 为等边三角形,BD 为中线,延长BC至E,使CE=CD,连接DE.若BD=3,则 DE 的长为 .
5.如图,D,E 分别是等边三角形ABC 的边BC,CA的延长线上的点,且CD=AE,连接AD,BE.
(1)求证:BE=AD;
知识点二 等边三角形的判定
6.下列说法:①三个角都相等的三角形是等边三角形;②有两个角等于60°的三角形是等边三角形;③有一个角是 60°的等腰三角形是等边三角形.其中正确的有 ( )
A.0个 B.1 个 C.2个 D.3 个
7.在△ABC中,如果AB=AC,∠A=∠C,那么△ABC 的形状为 .
8.如图,用圆规以直角顶点 O 为圆心,以适当长为半径画一条弧交两直角边于 A、B 两点.若再以 A 为圆心,以OA 为半径画弧,与弧 AB交于点C,连接OC,则∠BOC= °.
9.如图,在△ABC 中,AB=AC,D 为AC 的中点,DE⊥AB,DF⊥BC,垂足分别为点 E,F,且 DE=DF.求证:△ABC是等边三角形.
B层
10.如图,△ABC 是等边三角形,D 是边 BC 上一点,且∠ADC 的度数为(5x—20)°,则x 的值可能是( )
A.10 B.20 C.30 D.40
11.一艘轮船从海平面上 A 地出发,向北偏东50°的方向行驶 60海里到达 B 地,再由 B 地向南偏东10°的方向行驶 60海里到达 C 地,则 A,C两地相距 海里.
12.如图,在△ABC 中,AB=4 cm,BC=6 cm,∠B=60°,将△ABC 沿射线 BC 的方向平移2 cm 后,得 到 △A'B'C', 连 接 A'C, 则△A'B'C的周长为 .
13.如图,在四边形 ABCD 中,AB=AD,CB=CD,∠A =60°,点 E 为 AD 上一点,连接BD,CE交于点F,CE∥AB.
(1)判断△DEF 的形状,并说明理由;
(2)若AD=12,CE=8,求 CF 的长.
C层
14.已知△ABC 是等边三角形,将直角三角板DEF 如图放置,其中∠F=30°,让△ABC 在直角三角板的边 EF 上向右平移(点 C 与点 F重合时停止).
(1)如图①,当点 B 与点E 重合时,点 A 恰好落在直角三角板的斜边 DF 上,求证:EF=2BC;
(2)在△ABC平移过程中,AB、AC 与三角板斜边的交点分别为G、H,如图②,线段EB=AH 是否始终成立 请说明理由.
第 2 课时 含 30°角的直角三角形的性质
A层
知识点 含30°角的直角三角形的性质
1.如图,在 Rt△ABC 中,∠C =90°,AB =8,∠A=30°,则 BC 的长为 ( )
A.8 B.6 C.4 D.2
2.如图,在△ABC 中,∠B=90°,∠BAC=30°,AB=4,D 是BC延长线上一点,且CD=AC,连接AD,则AD 的长为 ( )
A.4 B.8 C.10 D.12
3.如图,在 Rt△ABC 中,∠C=90°,∠A=30°,线段 AB 的垂直平分线分别交AC、AB 于点 D、E,连接 BD.若CD=1,则 AD 的长为 .
4.如图,河流两岸a、b互相平行,点 A、B 是河岸a 上的两座建筑物,点 C、D 是河岸b 上的两点,A、B 的距离约为 200 米.某人在河岸 b 上的点P 处测得∠APC=75°,∠BPD=30°,则河流的宽度约为 米.
5.如图,在△ABC 中,∠ACB=90°,∠A=30°,AB=4,以点 B 为圆心,BC长为半径画弧,交边 AB 于点D,则CD 的长为 .
6.如图,在△ABC 中,∠ACB=90°,CD⊥AB 于点 D,如果∠DCB=30°,AB=12,那么 BD 的长为 .
7.如图,在△ABC中,AB=AC,BD⊥AC 于点D,∠CBD=15°,BD=3,求△ABC 的面积.
8.图①是某超市入口的双翼闸门,如图②,当它的双翼展开时,双翼边缘的端点 A 与 B 之间的距离为 10 cm,双翼的边缘 AC = BD =54 cm,且与闸 机 侧 立 面的夹 角∠PCA =∠BDQ=30°,求当双翼收起时,可以通过闸机的物体的最大宽度.
B层
9.如图,在△ABC 中,AB = AC,∠C =30°,AB⊥AD,AD=4,则 BC的长为 ( )
A.4 B.8 C.12 D.16
10.如图,在△ABC 中,AB=AC=6,∠BAC=120°,AD 是△ABC 的中线,AE 是∠BAD的平分线,DF∥AB交AE的延长线于点F,则 DF 的长是 ( )
A.5 B.2 C.4 D.3
11.如图,在 Rt△ABC中,∠C=90°,∠B =30°,BC=6.若E、F 是 BC 边上的两个动点,以 EF 为边的等边△EFP 的顶点 P 在△ABC内部或边上,则等边△EFP 的周长的最大值为 .
12.如图,△ABC 是等边三角形,D 是 BC 延长线上一点,DE⊥AB 于点 E,与 AC 相交于G点,EF⊥BC 于点 F.若 CD=3AE,CF=6,求 AC 的长.
13.某轮船由西向东航行,在 A 处测得小岛 P 的方位是北偏东 75°,又继续航行7 海里后,在B 处测得小岛 P 的方位是北偏东 60°.
(1)此时轮船与小岛 P 的距离 BP 是多少海里
(2)小岛 P 方圆3海里内有暗礁,如果轮船继续向东航行,请问轮船有没有触礁的危险 请说明理由.
C层
14.如图,在△ABC 中,∠A =90°,∠B =30°,AC=6cm,点 D 从点A 出发以1cm/s的速度向点 C 运动,同时点 E 从点 C 出发以2cm/s的速度向点 B 运动,运动的时间为t s,解决以下问题:
(1)当l 为何值时,△DEC 为等边三角形
(2)当t 为何值时,△DEC 为直角三角形
中小学教育资源及组卷应用平台
解题技巧专题:利用特殊角构造含30°角的
直角三角形解题
类型一 连接线段构造含30°角的直角三角形
1.如图,四边形 ABCD 中,AB = BC = 6 cm,∠A=120°,∠B=60°,∠C=150°,求AD 的长.
2.如图,△ABC 中,AB=AC,∠A=120°,DE垂直平分 AB 于点 D,交 BC 于点 E.求证:CE=2BE.
类型二 延长两边构造含30°角的直角三角形
3.如图,四边形 ABCD 中,AD=4,BC =1,∠A=30°,∠B=90°,∠ADC=120°,求 CD的长.
类型三 作垂线构造含30°角的直角三角形
4.如图,在△ABC中,∠B=60°,AB=10,BC=6,D 为BC上一点,且BD=2DC,连接AD.求证:AD=AC.
5.某市在“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境,已知AB=30m,AC=40m,∠BAC=150°,这种草皮的售价为a 元/m ,求购买这种草皮至少要多少元.
13.3.2 等边三角形
第1 课时 等边三角形的性质与判定1. B 2. C 3.30 4.3
5.(1) 证 明: ∵△ABC 是 等 边 三 角 形,∴∠BAC = ∠ACB = 60°, AC= AB.
∴∠BAE= ∠ACD = 120°. 在 △ABE 和△CAD 中, △CAD(SAS).∴BE=AD.
(2)解:∵△ABE≌△CAD,∴∠EBA =∠DAC. ∵ ∠ECB = 60°, ∠D = 40°,
6. D 7.等边三角形 8.30
9.证明:∵DE⊥AB,DF⊥BC,垂足分别为点E,F,∴∠AED=∠CFD=90°.∵D 为 AC 的中点,∴AD=DC.在 Rt△ADE 和 Rt△CDF中,DE=CDF,∴Rt△ADE≌Rt△CDF(HL).
∴∠A=∠C.∴ BA = BC.∵ AB = AC,
∴AB=BC=AC.∴△ABC是等边三角形.
10. B 11.60 12.12cm
13.解:(1)△DEF 是等边三角形,理由如下:∵AB=AD,∠A=60°,∴△ABD 是等边三角形.∴∠ABD=∠ADB=60°.∵CE∥AB,∴∠CED = ∠A = 60°,∠DFE =∠ABD = 60°. ∴ ∠CED = ∠ADB =∠DFE.∴△DEF 是等边三角形.
(2)如图,连接 AC 交 BD 于点O.∵AB=AD,CB=CD,∴AC 是 BD 的垂直平分线,即 AC⊥BD.∵AB = AD,∠BAD=60°, ∴∠BAC= ∠DAC = 30°.∵ CE ∥ AB, ∴∠BAC= ∠ACE =∠CAD = 30°.∴AE= CE = 8.∴ DE =AD-AE=12--8=4.∵△DEF 是等边三角形,∴EF=DE=4.∴CF=CE--EF=8--4=4.
14.(1) 证 明: ∵ △ABC 是 等 边 三 角 形,∴∠ACB=60°,AC = BC.∵∠F =30°, ∠F.∴ CF = AC.∴ CF = AC = BC.∴EF=2BC.
(2)解:成立.理由如下:∵△ABC是等边三角形,∴∠ACB=60°,AC=BC.∵∠F= ∠F.∴CH=CF.∵EF =2BC,∴BE +CF=BC.又∵AH+CH=AC,AC=BC,∴AH=BE.
第2课时 含30°角的直角三角形的性质1. C 2. B 3.2 4.100 5.2 6.3
7.解:∵BD⊥AC 于点 D,∠CBD = 15°,∴∠C=75°.∵AB=AC,∴∠ABC=∠C=75°.∴∠A =180°-∠ABC-∠C=30°.在Rt△ABD 中,∵∠ADB=90°,∠A =30°,∴AB=2BD=6.∴AC=AB=6.∴△ABC的面积
8.解:过 A 作AE⊥CP 于E,过 B 作BF⊥DQ于 F,则Rt△ACE中, 27(cm).同理可得BF=27cm.又∵点A 与B之间的距离为10cm,∴通过闸机的物体的最大宽度为27+10+27=64(cm).
答:当双翼收起时,可以通过闸机的物体的最大宽度为 64 cm.
9. C 10. D 11.9
12.解:∵△ABC为等边三角形,∴AB=BC=AC,∠A=∠B=∠ACB=60°.∵DE⊥AE,∴∠D=30°,∠AGE=30°.∴∠CGD=30°.∴CG=CD.设 AE=x,则CD=CG=3x.在Rt△AEG 中,AG=2AE=2x,∴AB=BC=AC = 5x.∴ BE = 4x, BF = 5x- 6.在
Rt△BEF中,易知∠BEF=30°,∴BE=2BF,即4x=2(5x-6).解得x=2.∴AC=5x=10.
13.解:(1) 过 P 作 PD ⊥ AB 于 点 D. 且∠PBD =∠PAB+∠APB,∠PAB=90°-75°=15°,∴∠APB= 15°. ∴ ∠PAB = ∠APB.∴BP=AB=7海里.
(2)没有触礁危险,理由如下:由(1)知 PB=7 海 里, 3.5海里>3海里.∴该轮船继续向东航行,没有触礁的危险.
14.解:(1)根据题意可得 AD=t cm,CD=(6-t) cm,CE=2t cm.∵△DEC为等边三角形,∴CD=CE.∴6-t=2t,解得t=2.∴当t 为2时,△DEC为等边三角形.
(2)∵∠B=30°,AC=6 cm,∴∠C=60°,BC=2AC=12 cm.①当∠DEC 为直角时, 即 t),解得 ②当∠EDC 为直角时, 即 解得t=3.∴当t为 或3时,△DEC为直角三角形.
解题技巧专题:利用特殊角构造含30°角的直角三角形解题
1.解:连接AC.∵AB=BC=6cm,∠B=60°,∴△ABC 是等边 三 角 形.∴AC = 6 cm,∠BAC =∠ACB = 60°.∵∠BAD = 120°,∠BCD =150°,∴∠ACD =90°,∠CAD =60°.∴∠D=30°.∴AD=2AC=12cm.
2.证明:连接AE.∵AB=AC,∠BAC=120°,∴∠B=∠C=30°.∵DE 垂直平分AB,∴ BE = AE. ∴ ∠BAE = ∠B = 30°.
∴CE=2AE.∵BE=AE,∴CE=2BE.
3.解:如图,延长 AD、BC交于点E.∵∠A=30°,∠B=90°,∴∠E=60°.
∵∠ADC = 120°,
∴∠EDC=60°.∴△EDC是等边三角形.设CD=CE=DE=x,则 AE=4+x,BE=1+x.在 Rt△ABE 中,∠A =30°,∴AE=2BE.∴2(1+x)=x+4.解得x=2.∴CD=2.
4.证明:如图,过 A 作AE⊥BC 于E. ∵AB = 10, ∠B = 60°,∴∠BAE=30°.∴BE= AB= 且 BD=2DC,∴BD=4,CD=2,CE=1.∴DE=1=CE.∴AE 垂直平分CD.∴AD=AC.
5.解:作 BA 边的高CD,与 BA 的延长线交于点 D.∵∠BAC= 150°, ∴∠DAC = 30°.∵CD⊥BD,AC = 40 m,∴CD = 20 m. 30× 20 = 300 ( m ). ∵ 草 皮 的 售 价 为a 元/m ,∴购买这种草皮至少要 300a元.
第 1 课时 等边三角形的性质与判定
A层
知识点一 等边三角形的性质
1.如图,AD 是等边三角形 ABC 的中线.若 BD=1cm,则 AC 的长为 ( )
A.1 cm B.2cm C.3cm D.4 cm
2.如图,AB∥CD,△ACE 为等边三角形,∠DCE=40°,则∠EAB 等于 ( )
A.40° B.30° C.20° D.15°
3.如图,在△ABC 中,BC 的垂直平分线分别交BC、AB 于点 E、F.若△AFC 是等边三角形,则∠B= °.
4.如图,已知△ABC 为等边三角形,BD 为中线,延长BC至E,使CE=CD,连接DE.若BD=3,则 DE 的长为 .
5.如图,D,E 分别是等边三角形ABC 的边BC,CA的延长线上的点,且CD=AE,连接AD,BE.
(1)求证:BE=AD;
知识点二 等边三角形的判定
6.下列说法:①三个角都相等的三角形是等边三角形;②有两个角等于60°的三角形是等边三角形;③有一个角是 60°的等腰三角形是等边三角形.其中正确的有 ( )
A.0个 B.1 个 C.2个 D.3 个
7.在△ABC中,如果AB=AC,∠A=∠C,那么△ABC 的形状为 .
8.如图,用圆规以直角顶点 O 为圆心,以适当长为半径画一条弧交两直角边于 A、B 两点.若再以 A 为圆心,以OA 为半径画弧,与弧 AB交于点C,连接OC,则∠BOC= °.
9.如图,在△ABC 中,AB=AC,D 为AC 的中点,DE⊥AB,DF⊥BC,垂足分别为点 E,F,且 DE=DF.求证:△ABC是等边三角形.
B层
10.如图,△ABC 是等边三角形,D 是边 BC 上一点,且∠ADC 的度数为(5x—20)°,则x 的值可能是( )
A.10 B.20 C.30 D.40
11.一艘轮船从海平面上 A 地出发,向北偏东50°的方向行驶 60海里到达 B 地,再由 B 地向南偏东10°的方向行驶 60海里到达 C 地,则 A,C两地相距 海里.
12.如图,在△ABC 中,AB=4 cm,BC=6 cm,∠B=60°,将△ABC 沿射线 BC 的方向平移2 cm 后,得 到 △A'B'C', 连 接 A'C, 则△A'B'C的周长为 .
13.如图,在四边形 ABCD 中,AB=AD,CB=CD,∠A =60°,点 E 为 AD 上一点,连接BD,CE交于点F,CE∥AB.
(1)判断△DEF 的形状,并说明理由;
(2)若AD=12,CE=8,求 CF 的长.
C层
14.已知△ABC 是等边三角形,将直角三角板DEF 如图放置,其中∠F=30°,让△ABC 在直角三角板的边 EF 上向右平移(点 C 与点 F重合时停止).
(1)如图①,当点 B 与点E 重合时,点 A 恰好落在直角三角板的斜边 DF 上,求证:EF=2BC;
(2)在△ABC平移过程中,AB、AC 与三角板斜边的交点分别为G、H,如图②,线段EB=AH 是否始终成立 请说明理由.
第 2 课时 含 30°角的直角三角形的性质
A层
知识点 含30°角的直角三角形的性质
1.如图,在 Rt△ABC 中,∠C =90°,AB =8,∠A=30°,则 BC 的长为 ( )
A.8 B.6 C.4 D.2
2.如图,在△ABC 中,∠B=90°,∠BAC=30°,AB=4,D 是BC延长线上一点,且CD=AC,连接AD,则AD 的长为 ( )
A.4 B.8 C.10 D.12
3.如图,在 Rt△ABC 中,∠C=90°,∠A=30°,线段 AB 的垂直平分线分别交AC、AB 于点 D、E,连接 BD.若CD=1,则 AD 的长为 .
4.如图,河流两岸a、b互相平行,点 A、B 是河岸a 上的两座建筑物,点 C、D 是河岸b 上的两点,A、B 的距离约为 200 米.某人在河岸 b 上的点P 处测得∠APC=75°,∠BPD=30°,则河流的宽度约为 米.
5.如图,在△ABC 中,∠ACB=90°,∠A=30°,AB=4,以点 B 为圆心,BC长为半径画弧,交边 AB 于点D,则CD 的长为 .
6.如图,在△ABC 中,∠ACB=90°,CD⊥AB 于点 D,如果∠DCB=30°,AB=12,那么 BD 的长为 .
7.如图,在△ABC中,AB=AC,BD⊥AC 于点D,∠CBD=15°,BD=3,求△ABC 的面积.
8.图①是某超市入口的双翼闸门,如图②,当它的双翼展开时,双翼边缘的端点 A 与 B 之间的距离为 10 cm,双翼的边缘 AC = BD =54 cm,且与闸 机 侧 立 面的夹 角∠PCA =∠BDQ=30°,求当双翼收起时,可以通过闸机的物体的最大宽度.
B层
9.如图,在△ABC 中,AB = AC,∠C =30°,AB⊥AD,AD=4,则 BC的长为 ( )
A.4 B.8 C.12 D.16
10.如图,在△ABC 中,AB=AC=6,∠BAC=120°,AD 是△ABC 的中线,AE 是∠BAD的平分线,DF∥AB交AE的延长线于点F,则 DF 的长是 ( )
A.5 B.2 C.4 D.3
11.如图,在 Rt△ABC中,∠C=90°,∠B =30°,BC=6.若E、F 是 BC 边上的两个动点,以 EF 为边的等边△EFP 的顶点 P 在△ABC内部或边上,则等边△EFP 的周长的最大值为 .
12.如图,△ABC 是等边三角形,D 是 BC 延长线上一点,DE⊥AB 于点 E,与 AC 相交于G点,EF⊥BC 于点 F.若 CD=3AE,CF=6,求 AC 的长.
13.某轮船由西向东航行,在 A 处测得小岛 P 的方位是北偏东 75°,又继续航行7 海里后,在B 处测得小岛 P 的方位是北偏东 60°.
(1)此时轮船与小岛 P 的距离 BP 是多少海里
(2)小岛 P 方圆3海里内有暗礁,如果轮船继续向东航行,请问轮船有没有触礁的危险 请说明理由.
C层
14.如图,在△ABC 中,∠A =90°,∠B =30°,AC=6cm,点 D 从点A 出发以1cm/s的速度向点 C 运动,同时点 E 从点 C 出发以2cm/s的速度向点 B 运动,运动的时间为t s,解决以下问题:
(1)当l 为何值时,△DEC 为等边三角形
(2)当t 为何值时,△DEC 为直角三角形
中小学教育资源及组卷应用平台
解题技巧专题:利用特殊角构造含30°角的
直角三角形解题
类型一 连接线段构造含30°角的直角三角形
1.如图,四边形 ABCD 中,AB = BC = 6 cm,∠A=120°,∠B=60°,∠C=150°,求AD 的长.
2.如图,△ABC 中,AB=AC,∠A=120°,DE垂直平分 AB 于点 D,交 BC 于点 E.求证:CE=2BE.
类型二 延长两边构造含30°角的直角三角形
3.如图,四边形 ABCD 中,AD=4,BC =1,∠A=30°,∠B=90°,∠ADC=120°,求 CD的长.
类型三 作垂线构造含30°角的直角三角形
4.如图,在△ABC中,∠B=60°,AB=10,BC=6,D 为BC上一点,且BD=2DC,连接AD.求证:AD=AC.
5.某市在“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境,已知AB=30m,AC=40m,∠BAC=150°,这种草皮的售价为a 元/m ,求购买这种草皮至少要多少元.
13.3.2 等边三角形
第1 课时 等边三角形的性质与判定1. B 2. C 3.30 4.3
5.(1) 证 明: ∵△ABC 是 等 边 三 角 形,∴∠BAC = ∠ACB = 60°, AC= AB.
∴∠BAE= ∠ACD = 120°. 在 △ABE 和△CAD 中, △CAD(SAS).∴BE=AD.
(2)解:∵△ABE≌△CAD,∴∠EBA =∠DAC. ∵ ∠ECB = 60°, ∠D = 40°,
6. D 7.等边三角形 8.30
9.证明:∵DE⊥AB,DF⊥BC,垂足分别为点E,F,∴∠AED=∠CFD=90°.∵D 为 AC 的中点,∴AD=DC.在 Rt△ADE 和 Rt△CDF中,DE=CDF,∴Rt△ADE≌Rt△CDF(HL).
∴∠A=∠C.∴ BA = BC.∵ AB = AC,
∴AB=BC=AC.∴△ABC是等边三角形.
10. B 11.60 12.12cm
13.解:(1)△DEF 是等边三角形,理由如下:∵AB=AD,∠A=60°,∴△ABD 是等边三角形.∴∠ABD=∠ADB=60°.∵CE∥AB,∴∠CED = ∠A = 60°,∠DFE =∠ABD = 60°. ∴ ∠CED = ∠ADB =∠DFE.∴△DEF 是等边三角形.
(2)如图,连接 AC 交 BD 于点O.∵AB=AD,CB=CD,∴AC 是 BD 的垂直平分线,即 AC⊥BD.∵AB = AD,∠BAD=60°, ∴∠BAC= ∠DAC = 30°.∵ CE ∥ AB, ∴∠BAC= ∠ACE =∠CAD = 30°.∴AE= CE = 8.∴ DE =AD-AE=12--8=4.∵△DEF 是等边三角形,∴EF=DE=4.∴CF=CE--EF=8--4=4.
14.(1) 证 明: ∵ △ABC 是 等 边 三 角 形,∴∠ACB=60°,AC = BC.∵∠F =30°, ∠F.∴ CF = AC.∴ CF = AC = BC.∴EF=2BC.
(2)解:成立.理由如下:∵△ABC是等边三角形,∴∠ACB=60°,AC=BC.∵∠F= ∠F.∴CH=CF.∵EF =2BC,∴BE +CF=BC.又∵AH+CH=AC,AC=BC,∴AH=BE.
第2课时 含30°角的直角三角形的性质1. C 2. B 3.2 4.100 5.2 6.3
7.解:∵BD⊥AC 于点 D,∠CBD = 15°,∴∠C=75°.∵AB=AC,∴∠ABC=∠C=75°.∴∠A =180°-∠ABC-∠C=30°.在Rt△ABD 中,∵∠ADB=90°,∠A =30°,∴AB=2BD=6.∴AC=AB=6.∴△ABC的面积
8.解:过 A 作AE⊥CP 于E,过 B 作BF⊥DQ于 F,则Rt△ACE中, 27(cm).同理可得BF=27cm.又∵点A 与B之间的距离为10cm,∴通过闸机的物体的最大宽度为27+10+27=64(cm).
答:当双翼收起时,可以通过闸机的物体的最大宽度为 64 cm.
9. C 10. D 11.9
12.解:∵△ABC为等边三角形,∴AB=BC=AC,∠A=∠B=∠ACB=60°.∵DE⊥AE,∴∠D=30°,∠AGE=30°.∴∠CGD=30°.∴CG=CD.设 AE=x,则CD=CG=3x.在Rt△AEG 中,AG=2AE=2x,∴AB=BC=AC = 5x.∴ BE = 4x, BF = 5x- 6.在
Rt△BEF中,易知∠BEF=30°,∴BE=2BF,即4x=2(5x-6).解得x=2.∴AC=5x=10.
13.解:(1) 过 P 作 PD ⊥ AB 于 点 D. 且∠PBD =∠PAB+∠APB,∠PAB=90°-75°=15°,∴∠APB= 15°. ∴ ∠PAB = ∠APB.∴BP=AB=7海里.
(2)没有触礁危险,理由如下:由(1)知 PB=7 海 里, 3.5海里>3海里.∴该轮船继续向东航行,没有触礁的危险.
14.解:(1)根据题意可得 AD=t cm,CD=(6-t) cm,CE=2t cm.∵△DEC为等边三角形,∴CD=CE.∴6-t=2t,解得t=2.∴当t 为2时,△DEC为等边三角形.
(2)∵∠B=30°,AC=6 cm,∴∠C=60°,BC=2AC=12 cm.①当∠DEC 为直角时, 即 t),解得 ②当∠EDC 为直角时, 即 解得t=3.∴当t为 或3时,△DEC为直角三角形.
解题技巧专题:利用特殊角构造含30°角的直角三角形解题
1.解:连接AC.∵AB=BC=6cm,∠B=60°,∴△ABC 是等边 三 角 形.∴AC = 6 cm,∠BAC =∠ACB = 60°.∵∠BAD = 120°,∠BCD =150°,∴∠ACD =90°,∠CAD =60°.∴∠D=30°.∴AD=2AC=12cm.
2.证明:连接AE.∵AB=AC,∠BAC=120°,∴∠B=∠C=30°.∵DE 垂直平分AB,∴ BE = AE. ∴ ∠BAE = ∠B = 30°.
∴CE=2AE.∵BE=AE,∴CE=2BE.
3.解:如图,延长 AD、BC交于点E.∵∠A=30°,∠B=90°,∴∠E=60°.
∵∠ADC = 120°,
∴∠EDC=60°.∴△EDC是等边三角形.设CD=CE=DE=x,则 AE=4+x,BE=1+x.在 Rt△ABE 中,∠A =30°,∴AE=2BE.∴2(1+x)=x+4.解得x=2.∴CD=2.
4.证明:如图,过 A 作AE⊥BC 于E. ∵AB = 10, ∠B = 60°,∴∠BAE=30°.∴BE= AB= 且 BD=2DC,∴BD=4,CD=2,CE=1.∴DE=1=CE.∴AE 垂直平分CD.∴AD=AC.
5.解:作 BA 边的高CD,与 BA 的延长线交于点 D.∵∠BAC= 150°, ∴∠DAC = 30°.∵CD⊥BD,AC = 40 m,∴CD = 20 m. 30× 20 = 300 ( m ). ∵ 草 皮 的 售 价 为a 元/m ,∴购买这种草皮至少要 300a元.
