基础提升专练 (含答案)2024—2025学年人教版数学八年级上册
文档属性
| 名称 | 基础提升专练 (含答案)2024—2025学年人教版数学八年级上册 | 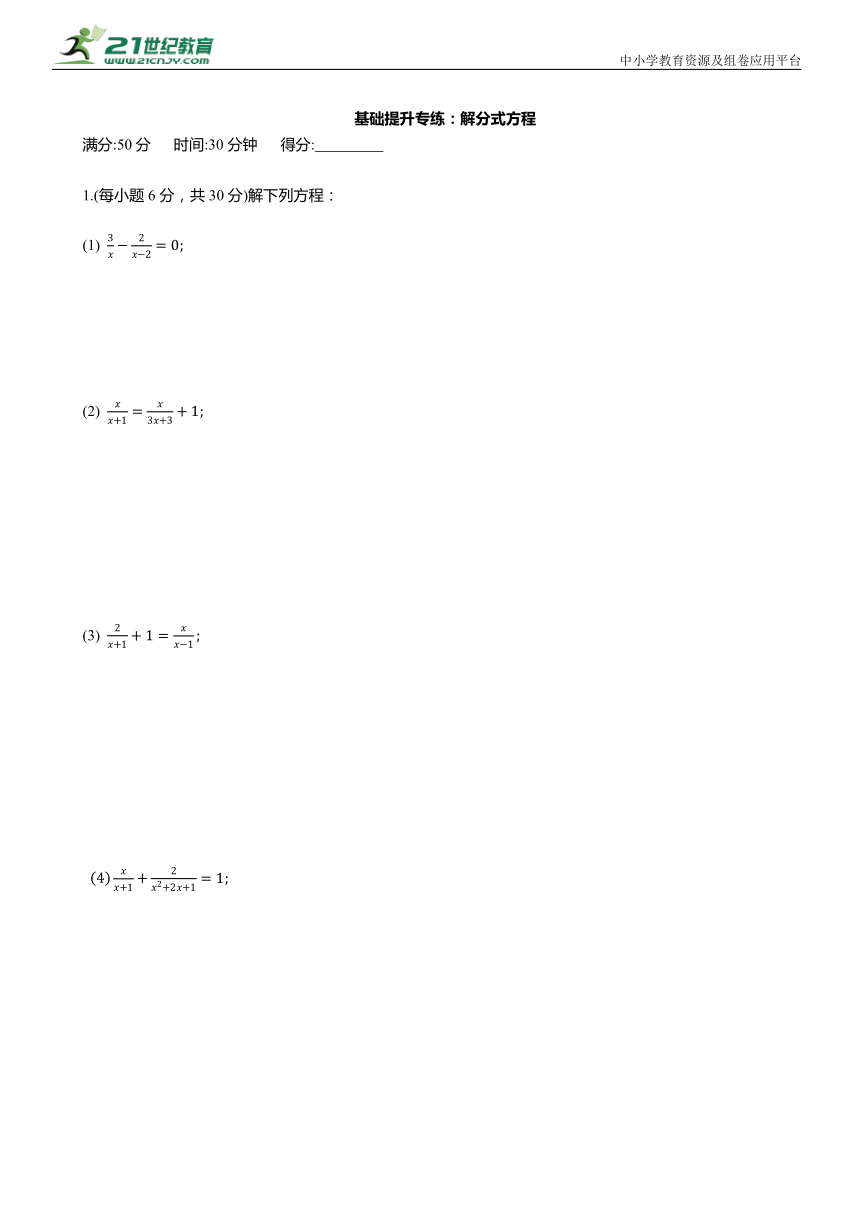 | |
| 格式 | docx | ||
| 文件大小 | 52.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 18:17:33 | ||
图片预览
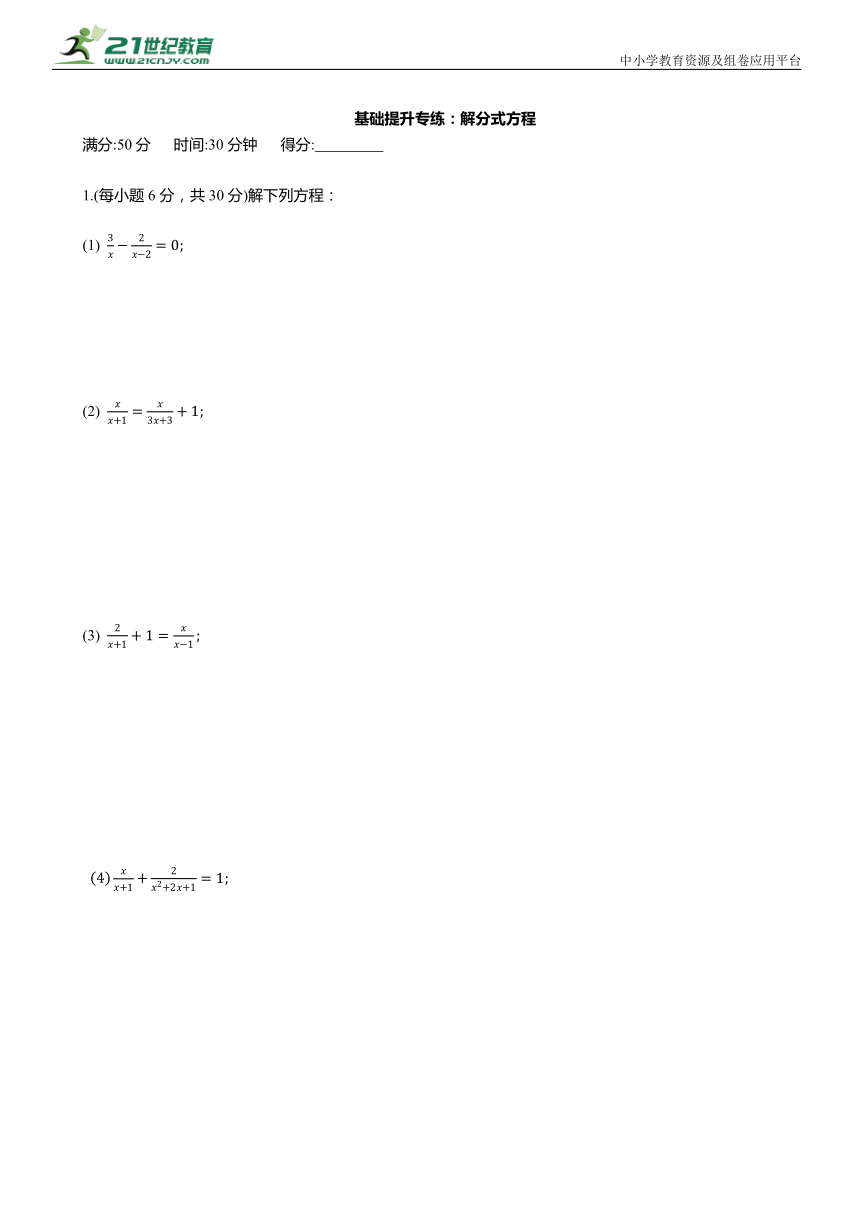


文档简介
基础提升专练:解分式方程
满分:50分 时间:30分钟 得分:
中小学教育资源及组卷应用平台
1.(每小题6分,共30分)解下列方程:
(1)
(2)
(3)
2.(10分)已知方程 的解与方程 的解相同,求a 的值.
3.(10分)已知点 A,B 在数轴上所对应的数分别为 若A,B 两点关于原点对称.
(1)当m=2时,求x 的值;
(2)若不存在满足条件的 x 值,求m 的值.
基础提升专练:分式方程的应用
满分:40分 时间:30分钟 得分:
1.(10分)“绿水青山就是金山银山.”为了更进一步优化环境,甲、乙两队承担河道整治任务.甲、乙两个工程队每天共整治河道1500 米,且甲整治3600米河道用的时间与乙工程队整治2400米所用的时间相等.问甲工程队每天整治河道多少米
2.(10分)为落实节约用水的政策,某旅游景点进行设施改造,将手拧水龙头全部更换成感应水龙头.已知该景点在设施改造后,平均每天用水量是原来的一半,20 吨水可以比原来多用5天.该景点在设施改造后平均每天用水多少吨
3.(10分)为了对学生进行革命传统教育,某中学开展了“清明节祭扫”活动.全校学生从学校同时出发,步行 4000米到达烈士纪念馆.学校要求九(1)班提前到达目的地,做好活动的准备工作.行走过程中,九(1)班步行的平均速度是其他班的1.25倍,结果比其他班提前10 分钟到达.分别求九(1)班、其他班步行的平均速度.
4.(10分)如图,某公司会计欲查询乙商品的进价,发现进货单已被墨水污染.进货单
商品 进价(元/件) 数量(件) 总金额(元)
甲 7200
乙 3200
商品采购员李阿姨和仓库保管员王师傅对采购情况回忆如下:
李阿姨:我记得甲商品进价比乙商品进价每件高50%.
王师傅:甲商品比乙商品的数量多40 件.
请你求出乙商品的进价,并帮助他们补全进货单.
基础提升专练:解分式方程
1.解:(1)去分母得3(x-2)-2x=0,去括号得3x-6-2x=0,解得x=6.检验:把x=6代入得x(x-2)=24≠0,∴分式方程的解为x=6.(6分)
(2)去分母得3x=x+3x+3,解得x=-3.检验:当x=--3时,3(x+1)≠0.∴分式方程的解为x=-3.(12分)
(3)方程两边同乘(x+1)(x--1),得2(x- 解得x=3.经检验,x=3是原方程的根,∴原方程的解为x=3.(18分)
(4)去分母得 解得x=1.经检验,x=1是分式方程的解.∴原方程的解为x=1.(24分)
(5)去分母得. 2),解得y=2.经检验,y=2不是分式方程的解,∴原分式方程无解.(30分)
2.解: 化为整式方程,得x(x- 解得x=-3.经检验,x=--3 是原方程的解,∴原方程的解是x=-3.(5分)将x=-3代入 2,解得 经检验, 是原方程的解. (10分)
3.解:(1)根据题意得 把m=2代入得 去分母得2--(x-8)=0,解得x=10.经检验,x=10是分式方程的解.∴x=10.(5分)
去分母得 m—(x—8)=0.已知不存在满足条件x 的值,即原分式方程无解,∴x=7.把x=7代入m--(x-8)=0得 m--(7--8)=0,解得 m =--1.(10分)
基础提升专练:分式方程的应用
1.解:设甲工程队每天整治河道x 米,则乙工程队每天整治河道(1500-x)米.根据题意得 解得 x=900.经检验,x=900是原方程的根.
答:甲工程队每天整治河道900米.(10分)
2.解:设该景点在设施改造后平均每天用水 x吨,则在改造前平均每天用水 2x 吨,根据题意.,得 解得x=2.经检验,x=2是原方程的解,且符合题意.
答:该景点在设施改造后平均每天用水 2 吨.(10分)
3.解:设其他班步行的平均速度为 x 米/分钟,则九(1)班步行的平均速度为1.25x米/分钟.依题意,得 解得x=80.经检验,x =80 是 原方 程 的解,且符 合 题 意.∴1.25x=100.
答:九(1)班步行的平均速度为100米/分钟,其他班步行的平均速度为 80 米/分钟.(10分)
4.解:设乙商品的进价为x 元/件,则甲商品的进价 为(1 + 50%) x 元/件. 依 题 意, 得 解得 x=40.经检验,x=40是原方程的解,且符合题意.∴(1+
答:甲商品的进价为60元/件,乙商品的进价为40元/件,购进甲商品 120件,购进乙商品80件.(10分)
满分:50分 时间:30分钟 得分:
中小学教育资源及组卷应用平台
1.(每小题6分,共30分)解下列方程:
(1)
(2)
(3)
2.(10分)已知方程 的解与方程 的解相同,求a 的值.
3.(10分)已知点 A,B 在数轴上所对应的数分别为 若A,B 两点关于原点对称.
(1)当m=2时,求x 的值;
(2)若不存在满足条件的 x 值,求m 的值.
基础提升专练:分式方程的应用
满分:40分 时间:30分钟 得分:
1.(10分)“绿水青山就是金山银山.”为了更进一步优化环境,甲、乙两队承担河道整治任务.甲、乙两个工程队每天共整治河道1500 米,且甲整治3600米河道用的时间与乙工程队整治2400米所用的时间相等.问甲工程队每天整治河道多少米
2.(10分)为落实节约用水的政策,某旅游景点进行设施改造,将手拧水龙头全部更换成感应水龙头.已知该景点在设施改造后,平均每天用水量是原来的一半,20 吨水可以比原来多用5天.该景点在设施改造后平均每天用水多少吨
3.(10分)为了对学生进行革命传统教育,某中学开展了“清明节祭扫”活动.全校学生从学校同时出发,步行 4000米到达烈士纪念馆.学校要求九(1)班提前到达目的地,做好活动的准备工作.行走过程中,九(1)班步行的平均速度是其他班的1.25倍,结果比其他班提前10 分钟到达.分别求九(1)班、其他班步行的平均速度.
4.(10分)如图,某公司会计欲查询乙商品的进价,发现进货单已被墨水污染.进货单
商品 进价(元/件) 数量(件) 总金额(元)
甲 7200
乙 3200
商品采购员李阿姨和仓库保管员王师傅对采购情况回忆如下:
李阿姨:我记得甲商品进价比乙商品进价每件高50%.
王师傅:甲商品比乙商品的数量多40 件.
请你求出乙商品的进价,并帮助他们补全进货单.
基础提升专练:解分式方程
1.解:(1)去分母得3(x-2)-2x=0,去括号得3x-6-2x=0,解得x=6.检验:把x=6代入得x(x-2)=24≠0,∴分式方程的解为x=6.(6分)
(2)去分母得3x=x+3x+3,解得x=-3.检验:当x=--3时,3(x+1)≠0.∴分式方程的解为x=-3.(12分)
(3)方程两边同乘(x+1)(x--1),得2(x- 解得x=3.经检验,x=3是原方程的根,∴原方程的解为x=3.(18分)
(4)去分母得 解得x=1.经检验,x=1是分式方程的解.∴原方程的解为x=1.(24分)
(5)去分母得. 2),解得y=2.经检验,y=2不是分式方程的解,∴原分式方程无解.(30分)
2.解: 化为整式方程,得x(x- 解得x=-3.经检验,x=--3 是原方程的解,∴原方程的解是x=-3.(5分)将x=-3代入 2,解得 经检验, 是原方程的解. (10分)
3.解:(1)根据题意得 把m=2代入得 去分母得2--(x-8)=0,解得x=10.经检验,x=10是分式方程的解.∴x=10.(5分)
去分母得 m—(x—8)=0.已知不存在满足条件x 的值,即原分式方程无解,∴x=7.把x=7代入m--(x-8)=0得 m--(7--8)=0,解得 m =--1.(10分)
基础提升专练:分式方程的应用
1.解:设甲工程队每天整治河道x 米,则乙工程队每天整治河道(1500-x)米.根据题意得 解得 x=900.经检验,x=900是原方程的根.
答:甲工程队每天整治河道900米.(10分)
2.解:设该景点在设施改造后平均每天用水 x吨,则在改造前平均每天用水 2x 吨,根据题意.,得 解得x=2.经检验,x=2是原方程的解,且符合题意.
答:该景点在设施改造后平均每天用水 2 吨.(10分)
3.解:设其他班步行的平均速度为 x 米/分钟,则九(1)班步行的平均速度为1.25x米/分钟.依题意,得 解得x=80.经检验,x =80 是 原方 程 的解,且符 合 题 意.∴1.25x=100.
答:九(1)班步行的平均速度为100米/分钟,其他班步行的平均速度为 80 米/分钟.(10分)
4.解:设乙商品的进价为x 元/件,则甲商品的进价 为(1 + 50%) x 元/件. 依 题 意, 得 解得 x=40.经检验,x=40是原方程的解,且符合题意.∴(1+
答:甲商品的进价为60元/件,乙商品的进价为40元/件,购进甲商品 120件,购进乙商品80件.(10分)
