第十二章全等三角形单元测试卷 (含答案)2024—2025学年人教版数学八年级上册
文档属性
| 名称 | 第十二章全等三角形单元测试卷 (含答案)2024—2025学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 638.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 19:56:28 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十二章全等三角形单元测试卷
满分:120分 时间:120分钟 得分:
一、选择题(每小题3 分,共30分)
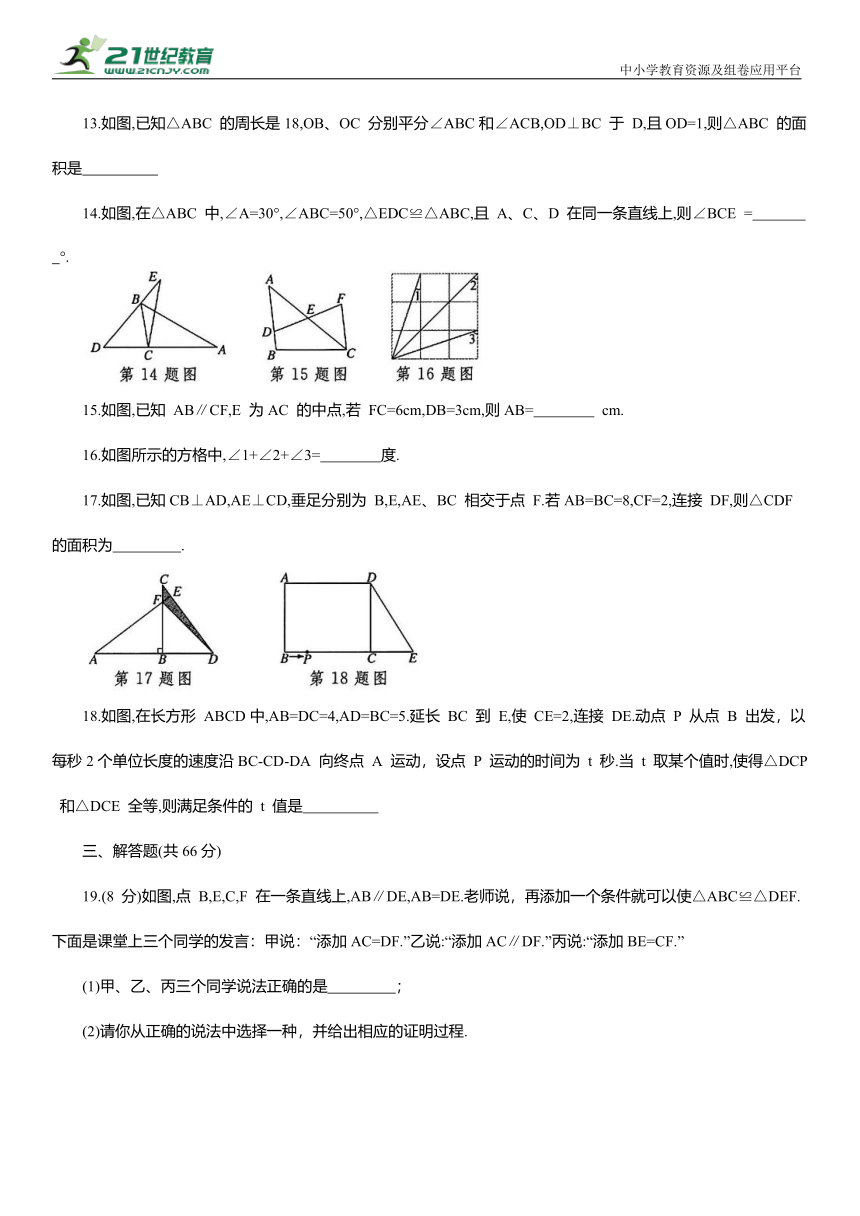
1.下列汽车标志中,不是由多个全等图形组成的是 ( )
2.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
A.76° B.62°
C.42° D.76°,62°或 42°都可以
3.如图,已知∠1=∠2,AC=AE,下列条件无法确定△ABC≌△ADE 的是 ( )
A.∠C=∠E B. BC=DE
C. AB=AD D.∠B=∠D
4.如图所示,为了测量水池两边 A,B间的距离,可以先过点A 作射线 AE,再过B 点作 BD⊥AE 于 D,在 AD 延长线上截取 连接 BC,则 BC 的长就是 A,B 间的距离,用来判定 的理由是 ( )
A. HL B. SAS C. ASA D. AAS
5.如图所示,由三条道路围成 其中 一个人从 B 处出发沿着 BC 行走了 800m,到达 D 处,AD恰为 的平分线,则此时这个人到AB 上的点的最短距离为 ( )
A.1000 m B.800m C.200m D.1800 m
6.根据下列已知条件,能画出唯一 的是 ( )
A. AB=3,BC=4,AC=8
7.如图,D 为△ABC 的边 BC 上一点, 且BF=DC,EC=BD,则∠EDF 等于 ( )
A.62° B.56° C.34° D.124°
8.如图,AB⊥CD,CE⊥AD 于 E,BF⊥AD 于 F.若. CD,CE=8,BF=6,AD=10,则EF的长为 ( )
A.4 C.3
9.如图,BE⊥AC 于点 D,且 AD=CD,BD=ED.若∠ABC=54°,则∠E的度数为 ( )
A.25° B.27° C.30° D.45°
10.如图,点 A,B 分别是∠NOP,∠MOP 平分线上的点,AB⊥OP 于点 E,BC⊥MN 于点 C,AD⊥MN 于点 D,则以下结论错误的是 ( )
A. AD+BC=AB
B.∠AOB=90°
C.与∠CBO 互余的角有 2个
D.点 O 是CD 的中点
二、填空题(每小题3分,共24分)
11.如图,在△ABD 和△ACD 中,∠1=∠2,若 (添加两条线段对应相等),则可以判定△ABD≌△ACD.
12.已知△ABC≌△DEF,BC=EF=4cm,△ABC 的面积是 ,那么△DEF 中 EF 边上的高是 cm.
13.如图,已知△ABC 的周长是18,OB、OC 分别平分∠ABC和∠ACB,OD⊥BC 于 D,且OD=1,则△ABC 的面积是
14.如图,在△ABC 中,∠A=30°,∠ABC=50°,△EDC≌△ABC,且 A、C、D 在同一条直线上,则∠BCE = °.
15.如图,已知 AB∥CF,E 为AC 的中点,若 FC=6cm,DB=3cm,则AB= cm.
16.如图所示的方格中,∠1+∠2+∠3= 度.
17.如图,已知CB⊥AD,AE⊥CD,垂足分别为 B,E,AE、BC 相交于点 F.若AB=BC=8,CF=2,连接 DF,则△CDF 的面积为 .
18.如图,在长方形 ABCD中,AB=DC=4,AD=BC=5.延长 BC 到 E,使 CE=2,连接 DE.动点 P 从点 B 出发,以每秒2个单位长度的速度沿BC-CD-DA 向终点 A 运动,设点 P 运动的时间为 t 秒.当 t 取某个值时,使得△DCP 和△DCE 全等,则满足条件的 t 值是
三、解答题(共66分)
19.(8 分)如图,点 B,E,C,F 在一条直线上,AB∥DE,AB=DE.老师说,再添加一个条件就可以使△ABC≌△DEF.下面是课堂上三个同学的发言:甲说:“添加AC=DF.”乙说:“添加AC∥DF.”丙说:“添加BE=CF.”
(1)甲、乙、丙三个同学说法正确的是 ;
(2)请你从正确的说法中选择一种,并给出相应的证明过程.
20.(8分)如图,在 中, 点 D 是斜边AB 上一点,且
(1)作 的平分线,交 BC 于点E;(要求尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接DE,求证:
21.(8分)小明与爸爸,妈妈在公园里荡秋千,如图,小明坐在秋千的起始位置 A 处,OA 与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1.2m 高的 B 处接住他后用力一推,爸爸在 C 处接住他,若妈妈与爸爸到 OA 的水平距离BD,CE 分别为1.6m 和2m,
(1)求证:
(2)爸爸是在距离地面 m高的地方接住小明的.
22.(10分)如图,在△ABC中,AB>AC,AD 为角平分线,P为AD 上任意一点,连接PB、PC,求证:AB-AC>PB-PC.(提示:在AB 上取一点E,使 AE=AC,连接PE)
23.(10分)如图,△ABC 和△ADE中,AB=AD,∠B=∠D,BC=DE.边 AD 与边 BC 交于点 P(不与点 B,C 重合),点B,E 在AD 异侧.
(1)若∠B=30°,∠APC=70°,求∠CAE 的度数;
(2)当AB⊥AC,AB=4,AC=3,BC=5时,设AP=x,请用含x的式子表示PD,并写出 PD 的最大值.
24.(10分)如图,在△ABC 中,AD 平分∠BAC,DG⊥BC且平分BC,DE⊥AB 于E,DF⊥AC 于 F.
(1)求证:BE=CF;
(2)若AB=8,AC=6,求AE,BE的长.
25.(12分)(1)特例探究:如图①,正方形ABCD 中,E、F 分别为 BC、CD 上两点, 探究 BE、EF、DF 之间的数量关系.小明是这么思考的:延长 FD,截取 连接AG,易证 从而得到 再由SAS证明 从而得出结论: ;
(2)一般探究:如图②,四边形 ABCD 中, 与 互补,E、F 分别是 BC、CD 上两点,且满足 探究 BE、EF、DF 之间的数量关系;
(3)实际应用:如图③,四边形ABCD 中, 直接写出四边形ABCD 的面积为 .
1. B 2. B 3. B 4. B 5. C
6. B 7. B 8. A 9. B
10. C 解析:∵点 A,B 分别是∠NOP,∠MOP 平分线上的点,AB⊥OP,BC⊥MN,AD⊥MN,∴AD=AE,BC=BE.∵AB=AE+BE,∴AB=AD+BC.故 A选项结论正确;易证 Rt△AOD≌Rt△AOE(HL),∴OD=OE,∠AOE=∠AOD.同理可 得 OC = OE, ∠BOC = ∠BOE, 故 B、D选项结论正确;与∠CBO 互余的角有∠COB,∠EOB,∠OAD,∠OAE,共4个,故 C 选项结论错误.故选 C.
11. AB=AC 12.8 13.9
14.20 15.9 16.135
17.6 解 析: ∵ CB ⊥ AD, AE ⊥ CD,
∴∠ABF=∠CBD = 90°,∠FEC= 90°.
∵∠AFB = ∠EFC,∴∠A = ∠C.在
△ABF 和△CBD 中,
∴△ABF≌△CBD(ASA).∴BF=BD.
∵BF=BC--CF=8--2=6,∴BD=6.
18.1.5 或5.5 解析:①当 P 在 BC 上时,由题意得 BP=2t,要使△DCP≌△DCE,则需CP=CE.∵CE=2,∴5--2t=2,t=1.5;②当P 在 CD 上时,不构成△DCP;③当 P在AD 上时,由题意得 BC+CD+DP=2t,∵BC=5,CD=4,∴DP =2t--9.要使△DCP≌△CDE,则需DP=CE,即2t-9=2,t=5.5.综上,当t =1.5 或 t =5.5 时,△DCP 和△DCE 全等.
19.解:(1)乙、丙(3分)
(2)选择乙同学的说法,证明:∵AB∥DE,∴∠B =∠DEF.∵AC∥DF,∴∠F =∠ACB.
∴ △ABE≌△BEF,∴△ABE≌△BEF(AAS).(8分)
选择丙同学的说法,证明:∵AB∥DE,∴∠B=∠DEF.∵BE=CF,∴BC=EF.在△ABC 和 △DEF 中, ∴△ABC≌△DEF(SAS).(8分)
20.(1)解:如图,AE 为所作.(3分)
(2)证明:∵AE 平分∠BAC,∴∠CAE=∠DAE. 在 △ACE 和 △ADE 中,
ABCELEDAEC:ADCE△ABE
(SAS).∴∠ADE=∠C=90°.∴DE⊥AB.(8分)
21.(1)证明:由题意可知∠CEO=∠BDO=90°,OB = OC.∵ ∠BOC = 90°, ∴ ∠COE +∠BOD = ∠BOD + ∠OBD = 90°.
∴∠COE=∠OBD.在△COE 和△OBD 中,
(AAS).(5 分)
(2)1.6(8分) 解析:∵△COE≌△OBD,∴CE=OD,OE = BD.∵BD = 1.6 m,
CE=2m,∴DE=OD-OE=CE-BD=2--1.6=0.4(m).∵AD=1.2m,∴AE=AD+DE=1.6m .
22.证明:如图,在 AB 上取一点E,使 AE = AC,连接 EP.∵AD 为角平分线,∴∠1=
∠2.在△AEP 和△ACP 中, ∴△AEP≌△ACP(SAS).∴EP= PC.在△BPE 中,BE>BP--EP=BP--PC,∴AB-AC>PB-PC.(10分)
23. 解: ( 1) 在 △ABC 与 △ADE 中,
∴∠BAC=∠DAE.∴∠BAC--∠DAC=∠DAE - ∠DAC. ∴ ∠BAD = ∠CAE.(3 分) ∵ ∠B = 30°, ∠APC = 70°,∴∠CAE=∠BAD = ∠APC - ∠B = (5分)
(2)∵AB⊥AC,∴∠BAC=90°.∵AB=4,∴AD=4.∴PD=4-x.∴当AD⊥BC时,x 最小,PD 最大. AC,可得 当x=2.4时,PD 的最大值为4-x=4-2.4=1.6.(10分)
24.(1)证明:如图,连接 DB,DC.∵ DG ⊥BC 且平分BC,∴∠DGB=∠DGC=90°,BG=CG.又∵DG=DG,∴△DGB≌△DGC (SAS). ∴ DB = DC. ∵AD 为∠BAC 的平分线,DE⊥AB,DF⊥AC,∴DE=DF,∠BED=∠AED=∠DFC=90°.(3 分)在 Rt△DBE 和Rt△DCF 中,PB=DC,∴Rt△DBE≌Rt△DCF(HL).∴BE=CF.(5分)
(2) 解: 在 Rt △ADE 和 Rt △ADF 中,DE=DF,,∴Rt△ADE≌Rt△ADF (HL).
∴AE=AF.(7分)∵AC+CF=AF,AE=AB-BE,∴AC+CF=AB--BE,即6+BE=8--BE.∴BE=1.∴AE=8--1=7.(10分)
25.解:(1)BE+DF=EF(3分)
(2)如图②,延长CB 至 G,使 BG=DF,连接AG.∵∠ABC+∠D=180°,∠ABC+∠ABG=180°,∴∠ABG=∠D.又∵BG=DF,AD=AB,∴△ADF≌△ABG(SAS).∴∠DAF=∠BAG,AF = AG. ∴ ∠FAG = ∠DAB.(6 分)又∵ ∴∠EAF=∠EAG.又∵AG=AF,AE=AE,∴△GAE≌△FAE(SAS).∴GE=EF,即 BE+DF=EF.(9分)
(3)18(12分) 解析:如图③,延长 CB,截取 BE = CD,连接 AE,证明△ACD ≌△AEB,得到S四边形ABCD=S△ACE=18.
第十二章全等三角形单元测试卷
满分:120分 时间:120分钟 得分:
一、选择题(每小题3 分,共30分)
1.下列汽车标志中,不是由多个全等图形组成的是 ( )
2.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
A.76° B.62°
C.42° D.76°,62°或 42°都可以
3.如图,已知∠1=∠2,AC=AE,下列条件无法确定△ABC≌△ADE 的是 ( )
A.∠C=∠E B. BC=DE
C. AB=AD D.∠B=∠D
4.如图所示,为了测量水池两边 A,B间的距离,可以先过点A 作射线 AE,再过B 点作 BD⊥AE 于 D,在 AD 延长线上截取 连接 BC,则 BC 的长就是 A,B 间的距离,用来判定 的理由是 ( )
A. HL B. SAS C. ASA D. AAS
5.如图所示,由三条道路围成 其中 一个人从 B 处出发沿着 BC 行走了 800m,到达 D 处,AD恰为 的平分线,则此时这个人到AB 上的点的最短距离为 ( )
A.1000 m B.800m C.200m D.1800 m
6.根据下列已知条件,能画出唯一 的是 ( )
A. AB=3,BC=4,AC=8
7.如图,D 为△ABC 的边 BC 上一点, 且BF=DC,EC=BD,则∠EDF 等于 ( )
A.62° B.56° C.34° D.124°
8.如图,AB⊥CD,CE⊥AD 于 E,BF⊥AD 于 F.若. CD,CE=8,BF=6,AD=10,则EF的长为 ( )
A.4 C.3
9.如图,BE⊥AC 于点 D,且 AD=CD,BD=ED.若∠ABC=54°,则∠E的度数为 ( )
A.25° B.27° C.30° D.45°
10.如图,点 A,B 分别是∠NOP,∠MOP 平分线上的点,AB⊥OP 于点 E,BC⊥MN 于点 C,AD⊥MN 于点 D,则以下结论错误的是 ( )
A. AD+BC=AB
B.∠AOB=90°
C.与∠CBO 互余的角有 2个
D.点 O 是CD 的中点
二、填空题(每小题3分,共24分)
11.如图,在△ABD 和△ACD 中,∠1=∠2,若 (添加两条线段对应相等),则可以判定△ABD≌△ACD.
12.已知△ABC≌△DEF,BC=EF=4cm,△ABC 的面积是 ,那么△DEF 中 EF 边上的高是 cm.
13.如图,已知△ABC 的周长是18,OB、OC 分别平分∠ABC和∠ACB,OD⊥BC 于 D,且OD=1,则△ABC 的面积是
14.如图,在△ABC 中,∠A=30°,∠ABC=50°,△EDC≌△ABC,且 A、C、D 在同一条直线上,则∠BCE = °.
15.如图,已知 AB∥CF,E 为AC 的中点,若 FC=6cm,DB=3cm,则AB= cm.
16.如图所示的方格中,∠1+∠2+∠3= 度.
17.如图,已知CB⊥AD,AE⊥CD,垂足分别为 B,E,AE、BC 相交于点 F.若AB=BC=8,CF=2,连接 DF,则△CDF 的面积为 .
18.如图,在长方形 ABCD中,AB=DC=4,AD=BC=5.延长 BC 到 E,使 CE=2,连接 DE.动点 P 从点 B 出发,以每秒2个单位长度的速度沿BC-CD-DA 向终点 A 运动,设点 P 运动的时间为 t 秒.当 t 取某个值时,使得△DCP 和△DCE 全等,则满足条件的 t 值是
三、解答题(共66分)
19.(8 分)如图,点 B,E,C,F 在一条直线上,AB∥DE,AB=DE.老师说,再添加一个条件就可以使△ABC≌△DEF.下面是课堂上三个同学的发言:甲说:“添加AC=DF.”乙说:“添加AC∥DF.”丙说:“添加BE=CF.”
(1)甲、乙、丙三个同学说法正确的是 ;
(2)请你从正确的说法中选择一种,并给出相应的证明过程.
20.(8分)如图,在 中, 点 D 是斜边AB 上一点,且
(1)作 的平分线,交 BC 于点E;(要求尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接DE,求证:
21.(8分)小明与爸爸,妈妈在公园里荡秋千,如图,小明坐在秋千的起始位置 A 处,OA 与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1.2m 高的 B 处接住他后用力一推,爸爸在 C 处接住他,若妈妈与爸爸到 OA 的水平距离BD,CE 分别为1.6m 和2m,
(1)求证:
(2)爸爸是在距离地面 m高的地方接住小明的.
22.(10分)如图,在△ABC中,AB>AC,AD 为角平分线,P为AD 上任意一点,连接PB、PC,求证:AB-AC>PB-PC.(提示:在AB 上取一点E,使 AE=AC,连接PE)
23.(10分)如图,△ABC 和△ADE中,AB=AD,∠B=∠D,BC=DE.边 AD 与边 BC 交于点 P(不与点 B,C 重合),点B,E 在AD 异侧.
(1)若∠B=30°,∠APC=70°,求∠CAE 的度数;
(2)当AB⊥AC,AB=4,AC=3,BC=5时,设AP=x,请用含x的式子表示PD,并写出 PD 的最大值.
24.(10分)如图,在△ABC 中,AD 平分∠BAC,DG⊥BC且平分BC,DE⊥AB 于E,DF⊥AC 于 F.
(1)求证:BE=CF;
(2)若AB=8,AC=6,求AE,BE的长.
25.(12分)(1)特例探究:如图①,正方形ABCD 中,E、F 分别为 BC、CD 上两点, 探究 BE、EF、DF 之间的数量关系.小明是这么思考的:延长 FD,截取 连接AG,易证 从而得到 再由SAS证明 从而得出结论: ;
(2)一般探究:如图②,四边形 ABCD 中, 与 互补,E、F 分别是 BC、CD 上两点,且满足 探究 BE、EF、DF 之间的数量关系;
(3)实际应用:如图③,四边形ABCD 中, 直接写出四边形ABCD 的面积为 .
1. B 2. B 3. B 4. B 5. C
6. B 7. B 8. A 9. B
10. C 解析:∵点 A,B 分别是∠NOP,∠MOP 平分线上的点,AB⊥OP,BC⊥MN,AD⊥MN,∴AD=AE,BC=BE.∵AB=AE+BE,∴AB=AD+BC.故 A选项结论正确;易证 Rt△AOD≌Rt△AOE(HL),∴OD=OE,∠AOE=∠AOD.同理可 得 OC = OE, ∠BOC = ∠BOE, 故 B、D选项结论正确;与∠CBO 互余的角有∠COB,∠EOB,∠OAD,∠OAE,共4个,故 C 选项结论错误.故选 C.
11. AB=AC 12.8 13.9
14.20 15.9 16.135
17.6 解 析: ∵ CB ⊥ AD, AE ⊥ CD,
∴∠ABF=∠CBD = 90°,∠FEC= 90°.
∵∠AFB = ∠EFC,∴∠A = ∠C.在
△ABF 和△CBD 中,
∴△ABF≌△CBD(ASA).∴BF=BD.
∵BF=BC--CF=8--2=6,∴BD=6.
18.1.5 或5.5 解析:①当 P 在 BC 上时,由题意得 BP=2t,要使△DCP≌△DCE,则需CP=CE.∵CE=2,∴5--2t=2,t=1.5;②当P 在 CD 上时,不构成△DCP;③当 P在AD 上时,由题意得 BC+CD+DP=2t,∵BC=5,CD=4,∴DP =2t--9.要使△DCP≌△CDE,则需DP=CE,即2t-9=2,t=5.5.综上,当t =1.5 或 t =5.5 时,△DCP 和△DCE 全等.
19.解:(1)乙、丙(3分)
(2)选择乙同学的说法,证明:∵AB∥DE,∴∠B =∠DEF.∵AC∥DF,∴∠F =∠ACB.
∴ △ABE≌△BEF,∴△ABE≌△BEF(AAS).(8分)
选择丙同学的说法,证明:∵AB∥DE,∴∠B=∠DEF.∵BE=CF,∴BC=EF.在△ABC 和 △DEF 中, ∴△ABC≌△DEF(SAS).(8分)
20.(1)解:如图,AE 为所作.(3分)
(2)证明:∵AE 平分∠BAC,∴∠CAE=∠DAE. 在 △ACE 和 △ADE 中,
ABCELEDAEC:ADCE△ABE
(SAS).∴∠ADE=∠C=90°.∴DE⊥AB.(8分)
21.(1)证明:由题意可知∠CEO=∠BDO=90°,OB = OC.∵ ∠BOC = 90°, ∴ ∠COE +∠BOD = ∠BOD + ∠OBD = 90°.
∴∠COE=∠OBD.在△COE 和△OBD 中,
(AAS).(5 分)
(2)1.6(8分) 解析:∵△COE≌△OBD,∴CE=OD,OE = BD.∵BD = 1.6 m,
CE=2m,∴DE=OD-OE=CE-BD=2--1.6=0.4(m).∵AD=1.2m,∴AE=AD+DE=1.6m .
22.证明:如图,在 AB 上取一点E,使 AE = AC,连接 EP.∵AD 为角平分线,∴∠1=
∠2.在△AEP 和△ACP 中, ∴△AEP≌△ACP(SAS).∴EP= PC.在△BPE 中,BE>BP--EP=BP--PC,∴AB-AC>PB-PC.(10分)
23. 解: ( 1) 在 △ABC 与 △ADE 中,
∴∠BAC=∠DAE.∴∠BAC--∠DAC=∠DAE - ∠DAC. ∴ ∠BAD = ∠CAE.(3 分) ∵ ∠B = 30°, ∠APC = 70°,∴∠CAE=∠BAD = ∠APC - ∠B = (5分)
(2)∵AB⊥AC,∴∠BAC=90°.∵AB=4,∴AD=4.∴PD=4-x.∴当AD⊥BC时,x 最小,PD 最大. AC,可得 当x=2.4时,PD 的最大值为4-x=4-2.4=1.6.(10分)
24.(1)证明:如图,连接 DB,DC.∵ DG ⊥BC 且平分BC,∴∠DGB=∠DGC=90°,BG=CG.又∵DG=DG,∴△DGB≌△DGC (SAS). ∴ DB = DC. ∵AD 为∠BAC 的平分线,DE⊥AB,DF⊥AC,∴DE=DF,∠BED=∠AED=∠DFC=90°.(3 分)在 Rt△DBE 和Rt△DCF 中,PB=DC,∴Rt△DBE≌Rt△DCF(HL).∴BE=CF.(5分)
(2) 解: 在 Rt △ADE 和 Rt △ADF 中,DE=DF,,∴Rt△ADE≌Rt△ADF (HL).
∴AE=AF.(7分)∵AC+CF=AF,AE=AB-BE,∴AC+CF=AB--BE,即6+BE=8--BE.∴BE=1.∴AE=8--1=7.(10分)
25.解:(1)BE+DF=EF(3分)
(2)如图②,延长CB 至 G,使 BG=DF,连接AG.∵∠ABC+∠D=180°,∠ABC+∠ABG=180°,∴∠ABG=∠D.又∵BG=DF,AD=AB,∴△ADF≌△ABG(SAS).∴∠DAF=∠BAG,AF = AG. ∴ ∠FAG = ∠DAB.(6 分)又∵ ∴∠EAF=∠EAG.又∵AG=AF,AE=AE,∴△GAE≌△FAE(SAS).∴GE=EF,即 BE+DF=EF.(9分)
(3)18(12分) 解析:如图③,延长 CB,截取 BE = CD,连接 AE,证明△ACD ≌△AEB,得到S四边形ABCD=S△ACE=18.
