第二十四章圆单元测试卷(含答案) 2024—2025学年人教版数学九年级上册
文档属性
| 名称 | 第二十四章圆单元测试卷(含答案) 2024—2025学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 546.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 20:05:47 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
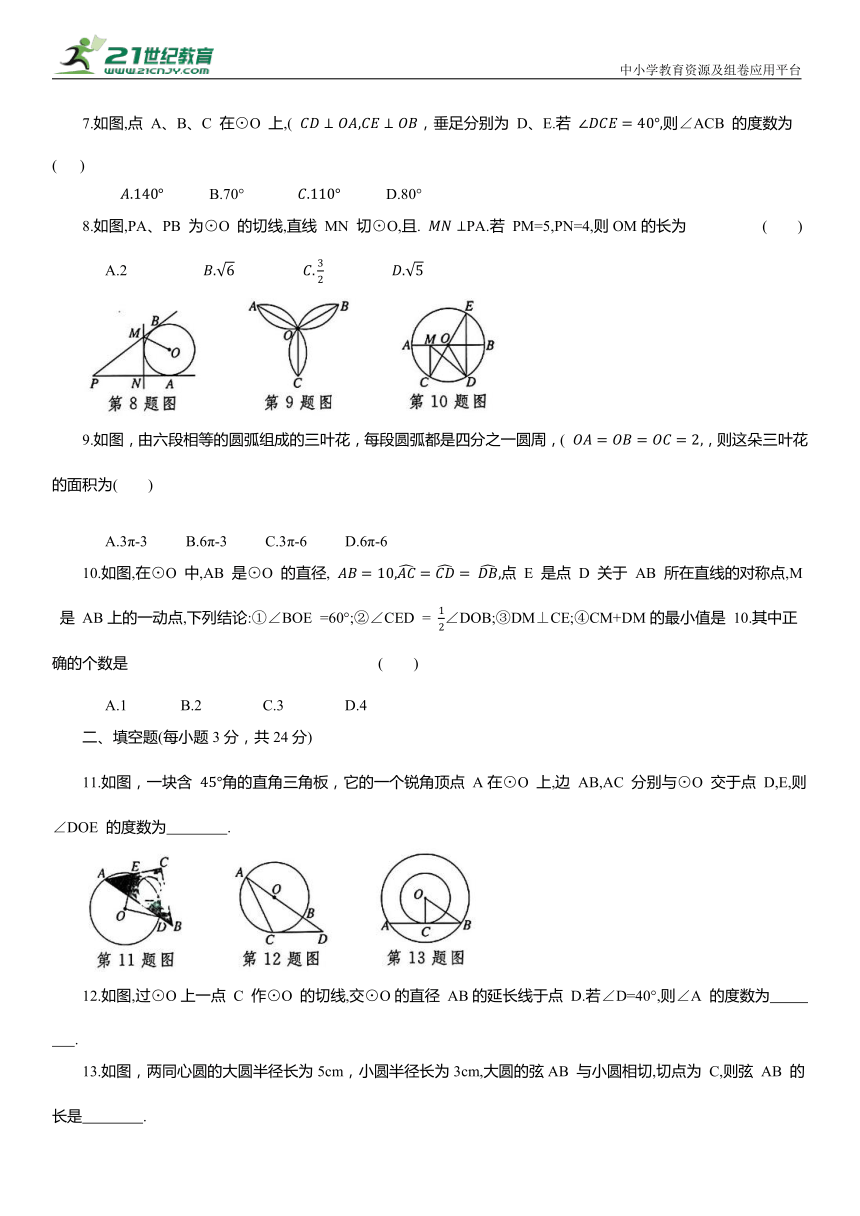
第二十四章圆单元测试卷
满分:120分 时间:120分钟 得分:
一、选择题(每小题3分,共30分)
1.已知⊙O 的半径是4,OP=3,则点 P 与⊙O 的位置关系是 ( )
A.点 P 在圆内 B.点 P 在圆上
C.点 P 在圆外 D.不能确定
2.下列说法不正确的是 ( )
A.圆既是中心对称图形又是轴对称图形
B.三角形的外心不一定在三角形的外部
C.相等的圆心角所对的弧相等
D.若直线 l 与圆没有公共点,则其位置关系是相离
3.用尺规作三角形的内心O,下列作图痕迹符合要求的是( )
4.如图,AB,AC 分别是⊙O 的直径和弦,( 于点 D,连接BD,BC,且AB=10,AC=8,则BD 的长为 ( )
B.4 D.4.8
5.一个圆锥的侧面展开图是半径为8的半圆,则该圆锥的全面积是 ( )
A.48π B.45π C.36π D.32π
6.如图,正方形ABCD 内接于⊙O, 则AB的长是( )
A.π C.2π
7.如图,点 A、B、C 在⊙O 上,( ,垂足分别为 D、E.若 则∠ACB 的度数为 ( )
B.70° D.80°
8.如图,PA、PB 为⊙O 的切线,直线 MN 切⊙O,且. PA.若 PM=5,PN=4,则OM的长为 ( )
A.2
9.如图,由六段相等的圆弧组成的三叶花,每段圆弧都是四分之一圆周,( ,则这朵三叶花的面积为( )
A.3π-3 B.6π-3 C.3π-6 D.6π-6
10.如图,在⊙O 中,AB 是⊙O 的直径, 点 E 是点 D 关于 AB 所在直线的对称点,M 是 AB上的一动点,下列结论:①∠BOE =60°;②∠CED = ∠DOB;③DM⊥CE;④CM+DM的最小值是 10.其中正确的个数是 ( )
A.1 B.2 C.3 D.4
二、填空题(每小题3分,共24分)
11.如图,一块含 角的直角三角板,它的一个锐角顶点 A在⊙O 上,边 AB,AC 分别与⊙O 交于点 D,E,则∠DOE 的度数为 .
12.如图,过⊙O上一点 C 作⊙O 的切线,交⊙O的直径 AB的延长线于点 D.若∠D=40°,则∠A 的度数为 .
13.如图,两同心圆的大圆半径长为5cm,小圆半径长为3cm,大圆的弦AB 与小圆相切,切点为 C,则弦 AB 的长是 .
14.如图,点 A、B、C、D、E 在⊙O上,且 则∠E+∠C= °.
15.在△ABC中,∠C=90°,AC=4,BC=3,则△ABC 的外接圆半径R 与内切圆半径r的差.
16.如图,在 ABCD中,AB17.已知在平面直角坐标系内,以点 P(--3,4)为圆心,r 为半径画圆,⊙P 与坐标轴恰好有三个交点,那么 r 的取值是 .
18.如图,在平面直角坐标系 xOy中,P 是直线y=2 上的一个动点,⊙P 的半径为1,直线 OQ 切⊙P 于点Q,则线段 OQ 的最小值为 .
三、解答题(共66分)
19.(8分)如图,在⊙O中,∠ABD=∠CDB.求证:AB=CD.
20.(8分)在学习圆与正多边形时,小昌、小雯两位同学设计了一个画圆内接正三角形的方法:
①如图,作直径AD;
②作半径OD 的垂直平分线,交⊙O于 B,C两点;
③连接AB、AC,那么△ABC 为所求的三角形.
(1)请你按照两位同学设计的画法,画出△ABC;
(2)请你判断两位同学的作法是否正确 如果正确,给出△ABC是正三角形的证明过程;如果不正确,请说明理由.
21.(8分)如图, 的平分线交 的外接圆于点D 的平分线交AD 于点E.
(1)求证:
(2)若 求 外接圆的半径.
22.(10分)我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种简易操作工具——三分角器.图①是它的示意图,其中 AB 与半圆O 的直径BC 在同一直线上,且 AB 的长度与半圆的半径相等;DB 与AC 垂直于点 B,DB 足够长.
使用方法如图②所示,若要把∠MEN 三等分,只需适当放置三分角器,使 DB 经过∠MEN 的顶点 E,点 A 落在边EM上,半圆O 与另一边EN 恰好相切,切点为F,则EB,EO就把∠MEN 三等分了.为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.
已知:如图②,点A,B,O,C 在同一直线上, 垂足为点 B, .
求证: .
23.(10 分)如图,正六边形 ABCDEF 内接于⊙O,BE 是⊙O 的直径,连接BF,过 F 作 交 BA 的延长线于G.
(1)求证:FG 是⊙O 的切线;
(2)已知 求图中阴影部分的面积.
24.(10分)AB,CD 是⊙O 的两条弦,直线AB,CD 互相垂直,垂足为点 E,连接AD,过点 B 作. 垂足为点 F ,直线 BF 交直线CD 于点 H.
(1)如图①,当点 E 在⊙O外时,连接BC,求证:BE 平分
(2)如图②,当点 E 在⊙O 内时,连接 AC,AH,求证:
25.(12分)如图,四边形 ABCD 内接于⊙O,对角线 AC 为⊙O 的直径,过点 C 作AC 的垂线交AD 的延长线于点E,过点 D 作⊙O 的切线交EC 于点 F.
(1)求证:
(2)①连接OD,当 的度数为 时,四边形ODFC 为正方形;
②若 求四边形ABCD 的最大面积.
1. A 2. C 3. D 4. C 5. A 6. A 7. C 8. D 9. C
10. C 解析:∵点 E 是点 D 关于 AB 的对称点, ∴①正确. ∴②正确.连接AD.∵AC=CD,∴AD⊥CE.∴只有 M 和 A 重合时,DM⊥CE.∴③错误.∵D,E 关于 AB 所在直线对称,∴连接 CE 交 AB 于 M,此时CM+DM=CE 最小. 180°,∴CE 为直径.∴CM+DM 的最小值是10.∴④正确.故选 C.
11.90°12.25° 13.8cm
14.210 15.1.5 17.4 或5
解析:如图①,连接 PQ、OP.∵直线OQ 切⊙P 于点Q,∴PQ⊥OQ.在 Rt△OPQ中,OQ= 当 OP 最小时,OQ 最小.如图②,当OP⊥直线 y=2时,OP 有最小值 2,∴OQ 的最小值为
19.证明:∵∠ABD =∠CDB,∴AD =BC, CD.(8分)
20.解:(1)△ABC 如图所示.(3分)
(2)两位同学的作法正确.证明如下:如图,连接BO,BD,OC.∵BC垂直平分 OD,∴BO=BD.又OB=OD,∴OB=OD=BD,即△BOD为正三角形.∴∠BOD = 60°,则∠AOB =180°— ∠BOD = 120°. 同 理 ∠AOC = 120°. ∴AB=AC = BC,即△ABC 为正 三角形.(8分)
21.(1) 证明:∵ BE 平 分∠ABC,AD 平分∠BAC, ∴ ∠ABE = ∠CBE, ∠BAE =∠CAD.∴BD=CD.∴∠DBC=∠CAD=∠BAE.(2分)∵∠DBE=∠CBE+∠DBC,∠DEB = ∠ABE+ ∠BAE, ∴∠DBE =∠DEB.∴DE=DB.(4分)
(2)解:由(1)得BD=CD,∴CD=BD=4.(5 分) ∵∠BAC = 90°, ∴ BC 是 直径. 4 .∴△ABC外接圆的半径为 (8分)
22.解:AB=OB,EN 切半圆O 于F,M、A、E三点共线(2分)
EB,EO 把∠MEN 三等分(3分)
证明:∵EB⊥AC,∴∠ABE=∠OBE=90°.∵AB=OB,BE=BE,∴△ABE≌△OBE(SAS).∴∠1=∠2.∵BE⊥OB,∴BE 是⊙O的切线.∵EN 切半圆 O 于 F,∴∠2=∠3.∴∠1=∠2=∠3.∴EB,EO 把∠MEN 三等分.(10分)
23.(1)证明:连接OF,AO,由题意可知 AB= 6 。.∴∠ABF=∠AFB=∠EBF=30°.∵OB =OF,∴∠OFB =∠OFB =30°.∴∠ABF =∠OFB.∴AB∥OF.∵FG⊥BA,∴OF⊥FG.又∵OF是⊙O的半径,∴FG 是⊙O的切线.(5分)
(2) 解: ∵ ∠AOF = 60°, OA = OF,∴△AOF 是 等 边 三 角 形. ∴∠AFO = 60°.∴∠AFG=30°.∴AF= 2AG.∵FG = 2 , ∴AO=4.∵∠AFB=∠OBF=30°,∴AF∥BE.∴S△ABF=S△AOF,∴图中阴影部分的面积等 于 扇形 AOF 的面积,为 (10分)
24.证明:(1) ∵四边形 ABCD 内接于⊙O,
∴∠D+∠ABC=180°.又∵∠EBC+∠ABC=
180°,∴∠D=∠EBC.∵HF⊥AD,AE⊥DH,
∴∠H +∠D = 90°,∠H +∠HBE = 90°.
∴∠HBE=∠D.∴∠HBE=∠EBC,即 BE平分∠HBC.(4分)
(2)连接CB.∵AB⊥CD,BF⊥AD,∴∠D+∠BAD=90°,∠ABH+∠BAD=90°.∴∠D=∠ABH.∵∠D=∠ABC,∴∠ABH=∠ABC.
∵AB⊥CD,∴∠CEB = ∠HEB = 90°.又
∵BE= BE, ∴ △BCE ≌ △BHE (ASA).
∴EC=EH.∴AC=AH.(10分)
25.(1)证明:∵AC 是⊙O 的直径,CE⊥AC,∴CE 是⊙O 的切线.又∵DF 是⊙O 的切线,且交 CE 于点 F,∴DF=CF.∴∠CDF =∠DCF.∵AC是⊙O 的直径,∴∠ADC=90°.
∴∠DCF+∠E=90°,∠CDF+∠EDF=90°.
∴∠E =∠EDF.∴DF = EF.∴EF= FC.(4分)
(2)解:①45°(8分) 解析:∵AC为⊙O的直径, ∴ ∠ADC = 90°. ∵ ∠ACD = 45°,∴∠DAC=45°.∴∠DOC=90°.∴∠DOC =∠ODF=∠OCF=90°.∴四边形 ODFC 为矩形.∵OD=OC,∴四边形ODFC为正方形.
②∵AC为⊙O的直径,∴∠ADC=∠ABC=90°.∵AD=4,DC=2,∴AC=√AD +CD =2 .∴要使四边形 ABCD 的面积最大,则△ABC 的面积最大.∴当 AC 边上的高最大,即△ABC 是等腰直角三角形时,△ABC 的面积最大.∴四边形 ABCD 的最大面积为 (12分)
第二十四章圆单元测试卷
满分:120分 时间:120分钟 得分:
一、选择题(每小题3分,共30分)
1.已知⊙O 的半径是4,OP=3,则点 P 与⊙O 的位置关系是 ( )
A.点 P 在圆内 B.点 P 在圆上
C.点 P 在圆外 D.不能确定
2.下列说法不正确的是 ( )
A.圆既是中心对称图形又是轴对称图形
B.三角形的外心不一定在三角形的外部
C.相等的圆心角所对的弧相等
D.若直线 l 与圆没有公共点,则其位置关系是相离
3.用尺规作三角形的内心O,下列作图痕迹符合要求的是( )
4.如图,AB,AC 分别是⊙O 的直径和弦,( 于点 D,连接BD,BC,且AB=10,AC=8,则BD 的长为 ( )
B.4 D.4.8
5.一个圆锥的侧面展开图是半径为8的半圆,则该圆锥的全面积是 ( )
A.48π B.45π C.36π D.32π
6.如图,正方形ABCD 内接于⊙O, 则AB的长是( )
A.π C.2π
7.如图,点 A、B、C 在⊙O 上,( ,垂足分别为 D、E.若 则∠ACB 的度数为 ( )
B.70° D.80°
8.如图,PA、PB 为⊙O 的切线,直线 MN 切⊙O,且. PA.若 PM=5,PN=4,则OM的长为 ( )
A.2
9.如图,由六段相等的圆弧组成的三叶花,每段圆弧都是四分之一圆周,( ,则这朵三叶花的面积为( )
A.3π-3 B.6π-3 C.3π-6 D.6π-6
10.如图,在⊙O 中,AB 是⊙O 的直径, 点 E 是点 D 关于 AB 所在直线的对称点,M 是 AB上的一动点,下列结论:①∠BOE =60°;②∠CED = ∠DOB;③DM⊥CE;④CM+DM的最小值是 10.其中正确的个数是 ( )
A.1 B.2 C.3 D.4
二、填空题(每小题3分,共24分)
11.如图,一块含 角的直角三角板,它的一个锐角顶点 A在⊙O 上,边 AB,AC 分别与⊙O 交于点 D,E,则∠DOE 的度数为 .
12.如图,过⊙O上一点 C 作⊙O 的切线,交⊙O的直径 AB的延长线于点 D.若∠D=40°,则∠A 的度数为 .
13.如图,两同心圆的大圆半径长为5cm,小圆半径长为3cm,大圆的弦AB 与小圆相切,切点为 C,则弦 AB 的长是 .
14.如图,点 A、B、C、D、E 在⊙O上,且 则∠E+∠C= °.
15.在△ABC中,∠C=90°,AC=4,BC=3,则△ABC 的外接圆半径R 与内切圆半径r的差.
16.如图,在 ABCD中,AB
18.如图,在平面直角坐标系 xOy中,P 是直线y=2 上的一个动点,⊙P 的半径为1,直线 OQ 切⊙P 于点Q,则线段 OQ 的最小值为 .
三、解答题(共66分)
19.(8分)如图,在⊙O中,∠ABD=∠CDB.求证:AB=CD.
20.(8分)在学习圆与正多边形时,小昌、小雯两位同学设计了一个画圆内接正三角形的方法:
①如图,作直径AD;
②作半径OD 的垂直平分线,交⊙O于 B,C两点;
③连接AB、AC,那么△ABC 为所求的三角形.
(1)请你按照两位同学设计的画法,画出△ABC;
(2)请你判断两位同学的作法是否正确 如果正确,给出△ABC是正三角形的证明过程;如果不正确,请说明理由.
21.(8分)如图, 的平分线交 的外接圆于点D 的平分线交AD 于点E.
(1)求证:
(2)若 求 外接圆的半径.
22.(10分)我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种简易操作工具——三分角器.图①是它的示意图,其中 AB 与半圆O 的直径BC 在同一直线上,且 AB 的长度与半圆的半径相等;DB 与AC 垂直于点 B,DB 足够长.
使用方法如图②所示,若要把∠MEN 三等分,只需适当放置三分角器,使 DB 经过∠MEN 的顶点 E,点 A 落在边EM上,半圆O 与另一边EN 恰好相切,切点为F,则EB,EO就把∠MEN 三等分了.为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.
已知:如图②,点A,B,O,C 在同一直线上, 垂足为点 B, .
求证: .
23.(10 分)如图,正六边形 ABCDEF 内接于⊙O,BE 是⊙O 的直径,连接BF,过 F 作 交 BA 的延长线于G.
(1)求证:FG 是⊙O 的切线;
(2)已知 求图中阴影部分的面积.
24.(10分)AB,CD 是⊙O 的两条弦,直线AB,CD 互相垂直,垂足为点 E,连接AD,过点 B 作. 垂足为点 F ,直线 BF 交直线CD 于点 H.
(1)如图①,当点 E 在⊙O外时,连接BC,求证:BE 平分
(2)如图②,当点 E 在⊙O 内时,连接 AC,AH,求证:
25.(12分)如图,四边形 ABCD 内接于⊙O,对角线 AC 为⊙O 的直径,过点 C 作AC 的垂线交AD 的延长线于点E,过点 D 作⊙O 的切线交EC 于点 F.
(1)求证:
(2)①连接OD,当 的度数为 时,四边形ODFC 为正方形;
②若 求四边形ABCD 的最大面积.
1. A 2. C 3. D 4. C 5. A 6. A 7. C 8. D 9. C
10. C 解析:∵点 E 是点 D 关于 AB 的对称点, ∴①正确. ∴②正确.连接AD.∵AC=CD,∴AD⊥CE.∴只有 M 和 A 重合时,DM⊥CE.∴③错误.∵D,E 关于 AB 所在直线对称,∴连接 CE 交 AB 于 M,此时CM+DM=CE 最小. 180°,∴CE 为直径.∴CM+DM 的最小值是10.∴④正确.故选 C.
11.90°12.25° 13.8cm
14.210 15.1.5 17.4 或5
解析:如图①,连接 PQ、OP.∵直线OQ 切⊙P 于点Q,∴PQ⊥OQ.在 Rt△OPQ中,OQ= 当 OP 最小时,OQ 最小.如图②,当OP⊥直线 y=2时,OP 有最小值 2,∴OQ 的最小值为
19.证明:∵∠ABD =∠CDB,∴AD =BC, CD.(8分)
20.解:(1)△ABC 如图所示.(3分)
(2)两位同学的作法正确.证明如下:如图,连接BO,BD,OC.∵BC垂直平分 OD,∴BO=BD.又OB=OD,∴OB=OD=BD,即△BOD为正三角形.∴∠BOD = 60°,则∠AOB =180°— ∠BOD = 120°. 同 理 ∠AOC = 120°. ∴AB=AC = BC,即△ABC 为正 三角形.(8分)
21.(1) 证明:∵ BE 平 分∠ABC,AD 平分∠BAC, ∴ ∠ABE = ∠CBE, ∠BAE =∠CAD.∴BD=CD.∴∠DBC=∠CAD=∠BAE.(2分)∵∠DBE=∠CBE+∠DBC,∠DEB = ∠ABE+ ∠BAE, ∴∠DBE =∠DEB.∴DE=DB.(4分)
(2)解:由(1)得BD=CD,∴CD=BD=4.(5 分) ∵∠BAC = 90°, ∴ BC 是 直径. 4 .∴△ABC外接圆的半径为 (8分)
22.解:AB=OB,EN 切半圆O 于F,M、A、E三点共线(2分)
EB,EO 把∠MEN 三等分(3分)
证明:∵EB⊥AC,∴∠ABE=∠OBE=90°.∵AB=OB,BE=BE,∴△ABE≌△OBE(SAS).∴∠1=∠2.∵BE⊥OB,∴BE 是⊙O的切线.∵EN 切半圆 O 于 F,∴∠2=∠3.∴∠1=∠2=∠3.∴EB,EO 把∠MEN 三等分.(10分)
23.(1)证明:连接OF,AO,由题意可知 AB= 6 。.∴∠ABF=∠AFB=∠EBF=30°.∵OB =OF,∴∠OFB =∠OFB =30°.∴∠ABF =∠OFB.∴AB∥OF.∵FG⊥BA,∴OF⊥FG.又∵OF是⊙O的半径,∴FG 是⊙O的切线.(5分)
(2) 解: ∵ ∠AOF = 60°, OA = OF,∴△AOF 是 等 边 三 角 形. ∴∠AFO = 60°.∴∠AFG=30°.∴AF= 2AG.∵FG = 2 , ∴AO=4.∵∠AFB=∠OBF=30°,∴AF∥BE.∴S△ABF=S△AOF,∴图中阴影部分的面积等 于 扇形 AOF 的面积,为 (10分)
24.证明:(1) ∵四边形 ABCD 内接于⊙O,
∴∠D+∠ABC=180°.又∵∠EBC+∠ABC=
180°,∴∠D=∠EBC.∵HF⊥AD,AE⊥DH,
∴∠H +∠D = 90°,∠H +∠HBE = 90°.
∴∠HBE=∠D.∴∠HBE=∠EBC,即 BE平分∠HBC.(4分)
(2)连接CB.∵AB⊥CD,BF⊥AD,∴∠D+∠BAD=90°,∠ABH+∠BAD=90°.∴∠D=∠ABH.∵∠D=∠ABC,∴∠ABH=∠ABC.
∵AB⊥CD,∴∠CEB = ∠HEB = 90°.又
∵BE= BE, ∴ △BCE ≌ △BHE (ASA).
∴EC=EH.∴AC=AH.(10分)
25.(1)证明:∵AC 是⊙O 的直径,CE⊥AC,∴CE 是⊙O 的切线.又∵DF 是⊙O 的切线,且交 CE 于点 F,∴DF=CF.∴∠CDF =∠DCF.∵AC是⊙O 的直径,∴∠ADC=90°.
∴∠DCF+∠E=90°,∠CDF+∠EDF=90°.
∴∠E =∠EDF.∴DF = EF.∴EF= FC.(4分)
(2)解:①45°(8分) 解析:∵AC为⊙O的直径, ∴ ∠ADC = 90°. ∵ ∠ACD = 45°,∴∠DAC=45°.∴∠DOC=90°.∴∠DOC =∠ODF=∠OCF=90°.∴四边形 ODFC 为矩形.∵OD=OC,∴四边形ODFC为正方形.
②∵AC为⊙O的直径,∴∠ADC=∠ABC=90°.∵AD=4,DC=2,∴AC=√AD +CD =2 .∴要使四边形 ABCD 的面积最大,则△ABC 的面积最大.∴当 AC 边上的高最大,即△ABC 是等腰直角三角形时,△ABC 的面积最大.∴四边形 ABCD 的最大面积为 (12分)
同课章节目录
