2021-2022学年重庆市秀山县八年级(下)期末数学试卷(含答案)
文档属性
| 名称 | 2021-2022学年重庆市秀山县八年级(下)期末数学试卷(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 607.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 19:19:04 | ||
图片预览

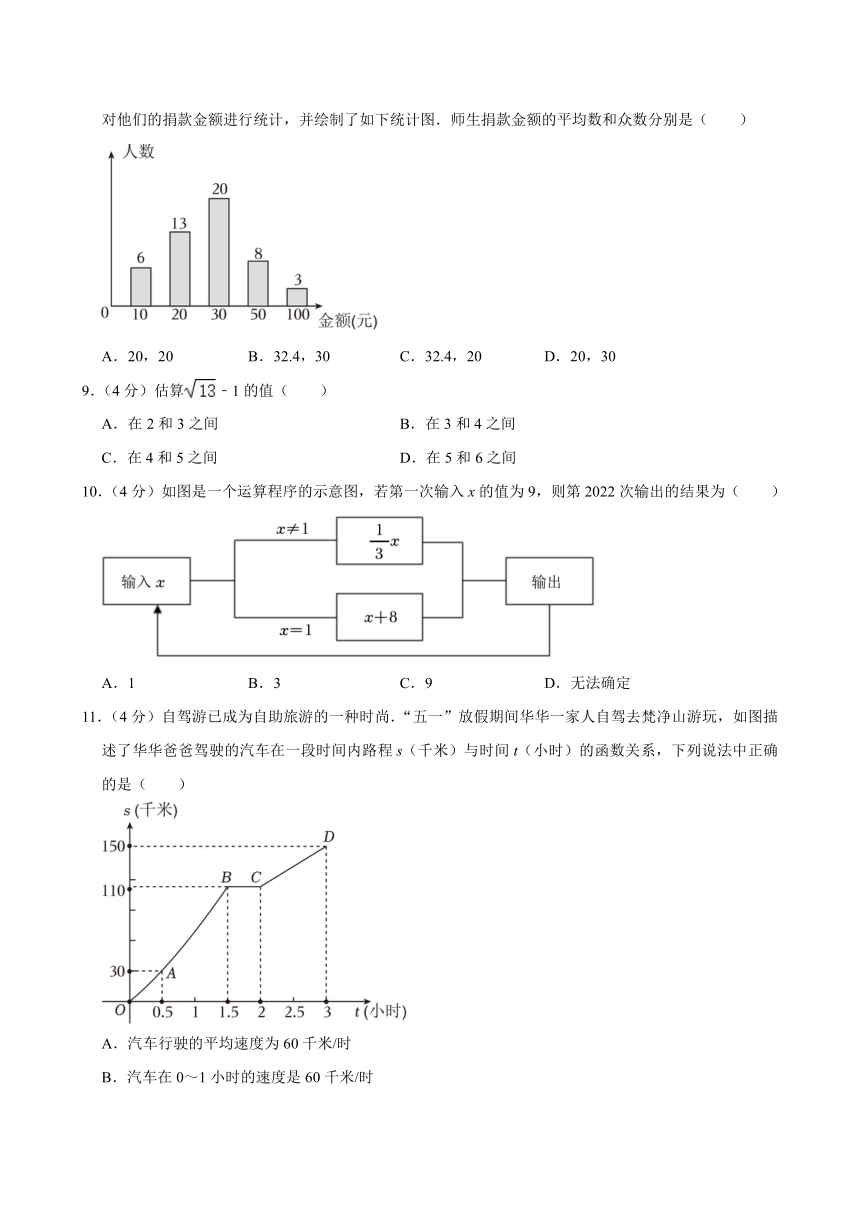

文档简介
2021-2022学年重庆市秀山县八年级(下)期末数学试卷
一、单选题:(本大题12个小题,每小题4分,共48分)请将答题卡上对应题号的正确答案标号涂黑。
1.(4分)函数y=中,自变量x的取值范围是( )
A.x>1 B.x≥1 C.x<1 D.x≤1
2.(4分)下列各式中,运算正确的是( )
A. B. C. D.2﹣
3.(4分)下表记录了甲、乙、丙、丁四名同学最近几次数学考试成绩的平均数与方差:要选择一名成绩好且发挥稳定的同学参加数学竞赛,应该选择( )
甲 乙 丙 丁
平均数(分) 92 95 95 92
方差 3.6 3.6 7.4 8.1
A.甲 B.乙 C.丙 D.丁
4.(4分)下列关于x的函数中,是正比例函数的为( )
A.y=x2 B.y= C.y= D.y=
5.(4分)下列四组线段中,不能作为直角三角形三条边的是( )
A.3,4,5 B.2,2,2 C.2,5,6 D.5,12,13
6.(4分)为了研究特殊四边形,李老师制作了这样一个教具(如图1):用钉子将四根木条钉成一个平行四边形框架ABCD,并在A与C、B与D两点之间分别用一根橡皮筋拉直固定.课上,李老师右手拿住木条BC,用左手向右推动框架至AB⊥BC(如图2).观察所得到的四边形,下列判断正确的是( )
A.∠BCA=45° B.BD的长度变小
C.AC=BD D.AC⊥BD
7.(4分)在下列图形性质中,平行四边形不一定具备的是( )
A.对角线相等 B.两组对边分别平行
C.两组对边分别相等 D.对角线互相平分
8.(4分)在一次为某位身患重病的小朋友募捐过程中,某年级有50师生通过微信平台奉献了爱心.小东对他们的捐款金额进行统计,并绘制了如下统计图.师生捐款金额的平均数和众数分别是( )
A.20,20 B.32.4,30 C.32.4,20 D.20,30
9.(4分)估算﹣1的值( )
A.在2和3之间 B.在3和4之间
C.在4和5之间 D.在5和6之间
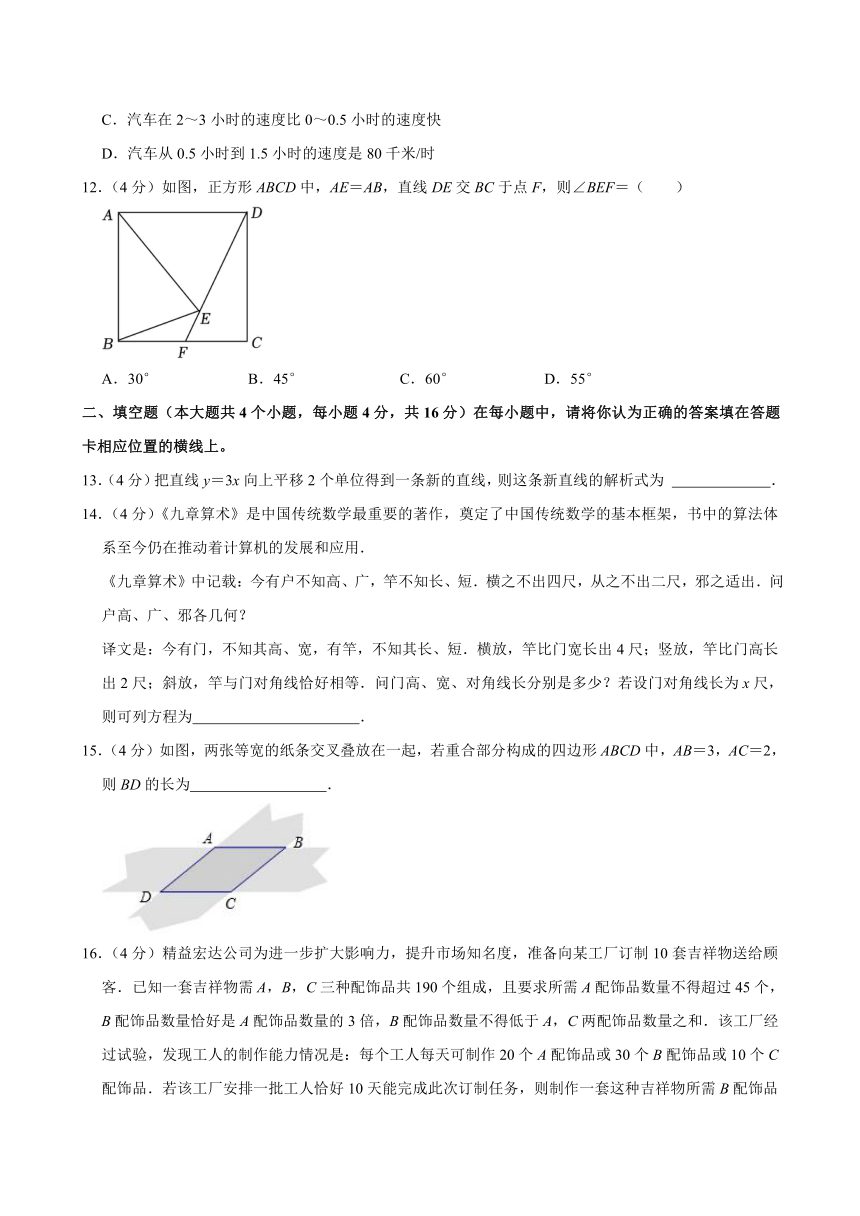
10.(4分)如图是一个运算程序的示意图,若第一次输入x的值为9,则第2022次输出的结果为( )
A.1 B.3 C.9 D.无法确定
11.(4分)自驾游已成为自助旅游的一种时尚.“五一”放假期间华华一家人自驾去梵净山游玩,如图描述了华华爸爸驾驶的汽车在一段时间内路程s(千米)与时间t(小时)的函数关系,下列说法中正确的是( )
A.汽车行驶的平均速度为60千米/时
B.汽车在0~1小时的速度是60千米/时
C.汽车在2~3小时的速度比0~0.5小时的速度快
D.汽车从0.5小时到1.5小时的速度是80千米/时
12.(4分)如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )
A.30° B.45° C.60° D.55°
二、填空题(本大题共4个小题,每小题4分,共16分)在每小题中,请将你认为正确的答案填在答题卡相应位置的横线上。
13.(4分)把直线y=3x向上平移2个单位得到一条新的直线,则这条新直线的解析式为 .
14.(4分)《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架,书中的算法体系至今仍在推动着计算机的发展和应用.
《九章算术》中记载:今有户不知高、广,竿不知长、短.横之不出四尺,从之不出二尺,邪之适出.问户高、广、邪各几何?
译文是:今有门,不知其高、宽,有竿,不知其长、短.横放,竿比门宽长出4尺;竖放,竿比门高长出2尺;斜放,竿与门对角线恰好相等.问门高、宽、对角线长分别是多少?若设门对角线长为x尺,则可列方程为 .
15.(4分)如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则BD的长为 .
16.(4分)精益宏达公司为进一步扩大影响力,提升市场知名度,准备向某工厂订制10套吉祥物送给顾客.已知一套吉祥物需A,B,C三种配饰品共190个组成,且要求所需A配饰品数量不得超过45个,B配饰品数量恰好是A配饰品数量的3倍,B配饰品数量不得低于A,C两配饰品数量之和.该工厂经过试验,发现工人的制作能力情况是:每个工人每天可制作20个A配饰品或30个B配饰品或10个C配饰品.若该工厂安排一批工人恰好10天能完成此次订制任务,则制作一套这种吉祥物所需B配饰品的数量是 个.
三、解答题(本大题2个小题,每小题8分,共16分)解答时每小题必须给出必要的演算过程或推理步骤,请将解答书写在答题卡中对应的位置上。
17.(8分)计算:
(1);
(2).
18.(8分)如图,在 ABCD中,AB>BC.BE平分∠ABC.
(1)尺规作图:作∠BAD的平分线交CD于点F.(保留作图痕迹,不写作法,不写结论)
(2)在(1)所作的图形中,BE与AF交于点P,求证:△ABP为直角三角形.
四、解答题(本大题7个小题,每小题10分,共70分)解答时每小题必须给出必要的演算过程或推理步骤,请将解答书写在答题卡中对应的位置上。
19.(10分)某校要从旺旺和墩墩两名同学中挑选一人参加全县生物实验竞赛,在最近的5次选拔测试中,他俩的成绩(单位:分)如下表:
第1次 第2次 第3次 第4次 第5次
旺旺成绩 65 75 100 85 75
墩墩成绩 70 90 80 80 80
根据上表解答下列问题:
(1)完成下表:
姓名 平均成绩/分 中位数/分 众数/分 方差
旺旺 80 75 75 140
墩墩
(2)在这5次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则旺旺、墩墩在5次测试中的优秀率各是多少;
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获一等奖,那么你认为应选谁参加比赛比较合适?说明你的理由.
20.(10分)已知y+4与x成正比例,且x=3时,y=2.
(1)求出y与x之间的函数关系式;
(2)在所给的直角坐标系(如图)中画出函数的图象;
(3)直接写出当﹣4≤y≤0时,自变量x的取值范围.
21.(10分)如图,在4×3正方形网格中,每个小正方形的边长都是1
(1)分别求出线段AB、CD的长度;
(2)在图中画线段EF、使得EF的长为,以AB、CD、EF三条线段能否构成直角三角形,并说明理由.
22.(10分)“每天一杯纯牛奶”已经成为人们生活的健康时尚,市场上对牛奶的需求越发增大.某乳品公司每月均需通过“飞快”快递公司向A地输送一批牛奶.“飞快”公司给出三种运费方案,具体如下:
方案一:每千克运费0.45元,按实际运输重量结算;
方案二:每月收取600元管理费用,再每千克运费0.15元;
方案三:每月收取1350元包干,不限运输重量.
设该公司每月运输牛奶x千克,选择方案一时,运费为y1元,选择方案二时,运费为y2元,选择方案三时,运费为y3元.
(1)请直接写出y1,y2,y3与x之间的关系式;
(2)在同一个坐标系中,若三种方案对应的函数图象如图所示,请求出点C,D,E的坐标,并直接写出如何选择方案更合算.
23.(10分)如图,在△ABC中,点D、E、F分别是边AC、AB、BC的中点,且.
(1)求证:四边形BFDE为矩形;
(2)若∠C=30°,BD=3,写出矩形BFDE的周长.
24.(10分)定义:对于三位自然数n=100a+10b+c(a≥1,b≤9,c≤9且a,b,c均为整数),若a+7=b+c,则称这样的三位自然数为“偶伴数”,并规定.例如:346是“偶伴数”,因为346,3+7=4+6,所以346是“偶伴数”,且,235不是“偶伴数”,因为2+7≠3+5,所以235不是“偶伴页.
(1)判断593与437是不是“偶伴数”,并说明理由;
(2)求大于600并能被7整除的所有“偶伴数”,并求出对应的所有F(n)的值.
25.(10分)已知,平行四边形ABCD中,连接BD,BD=BC,过点C作CE⊥BD,垂足为E,延长CE与AD相交于点F.
(1)如图1,若BE=4,DE=2.求线段AB的长;
(2)如图2,若∠CBD=45°,过点F作FG⊥AB于点G,连接BF、EG.求证:.
2021-2022学年重庆市秀山县八年级(下)期末数学试卷
参考答案
一、单选题:(本大题12个小题,每小题4分,共48分)请将答题卡上对应题号的正确答案标号涂黑。
1.(4分)函数y=中,自变量x的取值范围是( )
A.x>1 B.x≥1 C.x<1 D.x≤1
选:B.
2.(4分)下列各式中,运算正确的是( )
A. B. C. D.2﹣
选:B.
3.(4分)下表记录了甲、乙、丙、丁四名同学最近几次数学考试成绩的平均数与方差:要选择一名成绩好且发挥稳定的同学参加数学竞赛,应该选择( )
甲 乙 丙 丁
平均数(分) 92 95 95 92
方差 3.6 3.6 7.4 8.1
A.甲 B.乙 C.丙 D.丁
选:B.
4.(4分)下列关于x的函数中,是正比例函数的为( )
A.y=x2 B.y= C.y= D.y=
选:C.
5.(4分)下列四组线段中,不能作为直角三角形三条边的是( )
A.3,4,5 B.2,2,2 C.2,5,6 D.5,12,13
选:C.
6.(4分)为了研究特殊四边形,李老师制作了这样一个教具(如图1):用钉子将四根木条钉成一个平行四边形框架ABCD,并在A与C、B与D两点之间分别用一根橡皮筋拉直固定.课上,李老师右手拿住木条BC,用左手向右推动框架至AB⊥BC(如图2).观察所得到的四边形,下列判断正确的是( )
A.∠BCA=45° B.BD的长度变小
C.AC=BD D.AC⊥BD
选:C.
7.(4分)在下列图形性质中,平行四边形不一定具备的是( )
A.对角线相等 B.两组对边分别平行
C.两组对边分别相等 D.对角线互相平分
选:A.
8.(4分)在一次为某位身患重病的小朋友募捐过程中,某年级有50师生通过微信平台奉献了爱心.小东对他们的捐款金额进行统计,并绘制了如下统计图.师生捐款金额的平均数和众数分别是( )
A.20,20 B.32.4,30 C.32.4,20 D.20,30
选:B.
9.(4分)估算﹣1的值( )
A.在2和3之间 B.在3和4之间
C.在4和5之间 D.在5和6之间
选:A.
10.(4分)如图是一个运算程序的示意图,若第一次输入x的值为9,则第2022次输出的结果为( )
A.1 B.3 C.9 D.无法确定
选:C.
11.(4分)自驾游已成为自助旅游的一种时尚.“五一”放假期间华华一家人自驾去梵净山游玩,如图描述了华华爸爸驾驶的汽车在一段时间内路程s(千米)与时间t(小时)的函数关系,下列说法中正确的是( )
A.汽车行驶的平均速度为60千米/时
B.汽车在0~1小时的速度是60千米/时
C.汽车在2~3小时的速度比0~0.5小时的速度快
D.汽车从0.5小时到1.5小时的速度是80千米/时
选:D.
12.(4分)如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )
A.30° B.45° C.60° D.55°
选:B.
二、填空题(本大题共4个小题,每小题4分,共16分)在每小题中,请将你认为正确的答案填在答题卡相应位置的横线上。
13.(4分)把直线y=3x向上平移2个单位得到一条新的直线,则这条新直线的解析式为 y=3x+2 .
14.(4分)《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架,书中的算法体系至今仍在推动着计算机的发展和应用.
《九章算术》中记载:今有户不知高、广,竿不知长、短.横之不出四尺,从之不出二尺,邪之适出.问户高、广、邪各几何?
译文是:今有门,不知其高、宽,有竿,不知其长、短.横放,竿比门宽长出4尺;竖放,竿比门高长出2尺;斜放,竿与门对角线恰好相等.问门高、宽、对角线长分别是多少?若设门对角线长为x尺,则可列方程为 x2=(x﹣4)2+(x﹣2)2 .
15.(4分)如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则BD的长为 4 .
16.(4分)精益宏达公司为进一步扩大影响力,提升市场知名度,准备向某工厂订制10套吉祥物送给顾客.已知一套吉祥物需A,B,C三种配饰品共190个组成,且要求所需A配饰品数量不得超过45个,B配饰品数量恰好是A配饰品数量的3倍,B配饰品数量不得低于A,C两配饰品数量之和.该工厂经过试验,发现工人的制作能力情况是:每个工人每天可制作20个A配饰品或30个B配饰品或10个C配饰品.若该工厂安排一批工人恰好10天能完成此次订制任务,则制作一套这种吉祥物所需B配饰品的数量是 120 个.
三、解答题(本大题2个小题,每小题8分,共16分)解答时每小题必须给出必要的演算过程或推理步骤,请将解答书写在答题卡中对应的位置上。
17.(8分)计算:
(1);
(2).
【解答】解:(1)
=﹣()2+()2
=4﹣7+3
=0;
(2)
=1+9﹣(﹣1)+3
=10﹣+1+3
=11+2.
18.(8分)如图,在 ABCD中,AB>BC.BE平分∠ABC.
(1)尺规作图:作∠BAD的平分线交CD于点F.(保留作图痕迹,不写作法,不写结论)
(2)在(1)所作的图形中,BE与AF交于点P,求证:△ABP为直角三角形.
【解答】(1)解:如图,AF为所作;
(2)证明:∵四边形ABCD为平行四边形,
∴∠BAD+∠ABC=180°,
∵AF平分∠BAD,BE平分∠ABC,
∴∠PAB=∠BAD,∠PBA=∠ABC,
∴∠PAB+∠PBA=×180°=90°,
∴∠APB=90°,
∴△ABP为直角三角形.
四、解答题(本大题7个小题,每小题10分,共70分)解答时每小题必须给出必要的演算过程或推理步骤,请将解答书写在答题卡中对应的位置上。
19.(10分)某校要从旺旺和墩墩两名同学中挑选一人参加全县生物实验竞赛,在最近的5次选拔测试中,他俩的成绩(单位:分)如下表:
第1次 第2次 第3次 第4次 第5次
旺旺成绩 65 75 100 85 75
墩墩成绩 70 90 80 80 80
根据上表解答下列问题:
(1)完成下表:
姓名 平均成绩/分 中位数/分 众数/分 方差
旺旺 80 75 75 140
墩墩 80 80 80 40
(2)在这5次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则旺旺、墩墩在5次测试中的优秀率各是多少;
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获一等奖,那么你认为应选谁参加比赛比较合适?说明你的理由.
【解答】解:(1)墩墩的成绩:70、80、80、80、90,
∴平均成绩为:(70+80+80+80+90)÷5=80(分),
众数为:80分,中位数是80分;
方差为:[(70﹣80)2+(80﹣80)2+(80﹣80)2+(80﹣80)2+(90﹣80)2]÷5=40,
姓名 平均成绩/分 中位数/分 众数/分 方差
旺旺 80 75 75 140
墩墩 80 80 80 40
故答案为:80,80,80,40;
(2)∵旺旺的方差是140,墩墩的方差是40,而40<140,
∴墩墩成绩较稳定;
旺旺的优秀率为×100%=40%,墩墩的优秀率为×100%=80%;
(3)选墩墩参加比赛比较合适,理由:
虽然两人的平均数相同,但墩墩的成绩比旺旺稳定,且优秀率比旺旺的高,因此选墩墩参加比赛比较合适.
20.(10分)已知y+4与x成正比例,且x=3时,y=2.
(1)求出y与x之间的函数关系式;
(2)在所给的直角坐标系(如图)中画出函数的图象;
(3)直接写出当﹣4≤y≤0时,自变量x的取值范围.
【解答】解:(1)∵y+4与x成正比例,
∴设y+4=kx(k≠0),
∵当x=3时,y=2,
∴2+4=3k,
解得k=2,
∴y+4=2x,
函数关系式为:y=2x﹣4;
(2)当x=0时,y=﹣4,
当y=0时,2x﹣4=0,解得x=2,
所以,函数图象经过点(0,﹣4),(2,0),
函数图象如图:
(3)由图象得:当﹣4≤y≤0时,自变量x的取值范围是:0≤x≤2.
21.(10分)如图,在4×3正方形网格中,每个小正方形的边长都是1
(1)分别求出线段AB、CD的长度;
(2)在图中画线段EF、使得EF的长为,以AB、CD、EF三条线段能否构成直角三角形,并说明理由.
【解答】解:(1)AB==;CD==2.
(2)如图,EF==,
∵CD2+EF2=8+5=13,AB2=13,
∴CD2+EF2=AB2,
∴以AB、CD、EF三条线可以组成直角三角形.
22.(10分)“每天一杯纯牛奶”已经成为人们生活的健康时尚,市场上对牛奶的需求越发增大.某乳品公司每月均需通过“飞快”快递公司向A地输送一批牛奶.“飞快”公司给出三种运费方案,具体如下:
方案一:每千克运费0.45元,按实际运输重量结算;
方案二:每月收取600元管理费用,再每千克运费0.15元;
方案三:每月收取1350元包干,不限运输重量.
设该公司每月运输牛奶x千克,选择方案一时,运费为y1元,选择方案二时,运费为y2元,选择方案三时,运费为y3元.
(1)请直接写出y1,y2,y3与x之间的关系式;
(2)在同一个坐标系中,若三种方案对应的函数图象如图所示,请求出点C,D,E的坐标,并直接写出如何选择方案更合算.
【解答】解:(1)由题意得y1=0.45x;y2=0.15x+600;y3=1350;
(2)解方程0.45x=0.15x+600,得x=2000,
0.45×2000=900,
故点C的坐标为(2000,900);
解方程0.45x=1350,得x=3000,
故点D的坐标为(3000,1350);
解方程0.15x+600=1350,得x=5000,
故点E的坐标为(5000,1350);
由图象可知,当0<x≤2000时,采用方案一更合算;当450<x≤5000时,采用方案二更合算;当x>5000时,采用方案三更合算.
23.(10分)如图,在△ABC中,点D、E、F分别是边AC、AB、BC的中点,且.
(1)求证:四边形BFDE为矩形;
(2)若∠C=30°,BD=3,写出矩形BFDE的周长.
【解答】(1)证明:∵点D、E、F分别是边AC、AB、BC的中点,
∴DE、DF是△ABC的中位线,
∴DE∥BC,DF∥AB,
∴四边形BFDE是平行四边形,
∵D是AC的中点,且,
∴△ABC是直角三角形,且∠ABC=90°,
∴平行四边形BFDE为矩形;
(2)解:由(1)可知,四边形BFDE为矩形,
∴BE=DF,BF=DE,∠DFB=90°,
∵BD=AC=CD,
∴∠DBF=∠C=30°,
∴DF=BD=,
∴BF===,
∴矩形BFDE的周长=2(DF+BF)=3+3.
24.(10分)定义:对于三位自然数n=100a+10b+c(a≥1,b≤9,c≤9且a,b,c均为整数),若a+7=b+c,则称这样的三位自然数为“偶伴数”,并规定.例如:346是“偶伴数”,因为346,3+7=4+6,所以346是“偶伴数”,且,235不是“偶伴数”,因为2+7≠3+5,所以235不是“偶伴页.
(1)判断593与437是不是“偶伴数”,并说明理由;
(2)求大于600并能被7整除的所有“偶伴数”,并求出对应的所有F(n)的值.
【解答】解:(1)∵5+7=3+9,4+7≠3+7
∴593是偶伴数,437不是偶伴数;
(2)①当a=6时,则b+c=13,且能被7整除,
偶伴数为658,此时
F(658)=;
②当a=7时,则b+c=14,且能被7整除,
偶伴数为777,此时
F(777)=;
③当a=8,则b+c=15,且能被7整除,
偶伴数为896,此时
F(896)=;
④当a=9,则b+c=16,且能被7整除,
此时不存在满足条件的偶伴数,
综上分析,大于600并能被7整除的所有偶伴数是658或777或896,对应的F(n)的值分别是或或.
25.(10分)已知,平行四边形ABCD中,连接BD,BD=BC,过点C作CE⊥BD,垂足为E,延长CE与AD相交于点F.
(1)如图1,若BE=4,DE=2.求线段AB的长;
(2)如图2,若∠CBD=45°,过点F作FG⊥AB于点G,连接BF、EG.求证:.
【解答】(1)解:∵BE=4,DE=2,
∴BD=BE+DE=6,
∵BD=BC,
∴BC=6,
∵CE⊥BD,
∴∠BEC=∠DEC=90°,
在Rt△BEC中,由勾股定理得CE==2,
在Rt△DEC中,由勾股定理得CD==2,
∵四边形ABCD是平行四边形,
∴AB=CD=2;
(2)证明:∵CE⊥AD,
∴∠BEC=∠CED=90°,
∵∠CBE=45°,
∴△BCE是等腰直角三角形,
∴∠BCE=45°,CE=BE,
∵BC∥AD,
∴∠BDF=45°,∠ACC+∠DCB=180°,
设∠DCE=x,
∴∠BCD=45°+x,
∵BC=BD,
∴∠BDC=∠BCE=45°+x,
∵∠ECD+∠EDC=90°,
∴x+45°+x=90°,
∴x=22.5°,
∴∠ECD=22.5°,∠BDC=67.5°,
∵∠BCF=∠ADE=∠DFE=∠CBE=45°,
∴DE=EF,
∴CF=BD,
在△CFD和△BDF中,
,
∴△CFD≌△BDF(SAS),
∴∠DBF=∠DCF=22.5°,
∵AB∥CD,
∴∠ABC=180°﹣∠BCD=180°﹣67.5°=112.5°,
∴∠ABD=67.5°,
∵FG⊥AB,
∴∠BGF=∠AEF=90°,
∴∠EGF=∠EAF=22.5°,
∴∠AGE=67.5°,
∵∠CAD=∠ACB=67.5°,
∴∠EAG=∠AGE,
∴AE=GE,
∵AC=AB=AE,
∴BE+EC=AE+EC=AC=EG.
一、单选题:(本大题12个小题,每小题4分,共48分)请将答题卡上对应题号的正确答案标号涂黑。
1.(4分)函数y=中,自变量x的取值范围是( )
A.x>1 B.x≥1 C.x<1 D.x≤1
2.(4分)下列各式中,运算正确的是( )
A. B. C. D.2﹣
3.(4分)下表记录了甲、乙、丙、丁四名同学最近几次数学考试成绩的平均数与方差:要选择一名成绩好且发挥稳定的同学参加数学竞赛,应该选择( )
甲 乙 丙 丁
平均数(分) 92 95 95 92
方差 3.6 3.6 7.4 8.1
A.甲 B.乙 C.丙 D.丁
4.(4分)下列关于x的函数中,是正比例函数的为( )
A.y=x2 B.y= C.y= D.y=
5.(4分)下列四组线段中,不能作为直角三角形三条边的是( )
A.3,4,5 B.2,2,2 C.2,5,6 D.5,12,13
6.(4分)为了研究特殊四边形,李老师制作了这样一个教具(如图1):用钉子将四根木条钉成一个平行四边形框架ABCD,并在A与C、B与D两点之间分别用一根橡皮筋拉直固定.课上,李老师右手拿住木条BC,用左手向右推动框架至AB⊥BC(如图2).观察所得到的四边形,下列判断正确的是( )
A.∠BCA=45° B.BD的长度变小
C.AC=BD D.AC⊥BD
7.(4分)在下列图形性质中,平行四边形不一定具备的是( )
A.对角线相等 B.两组对边分别平行
C.两组对边分别相等 D.对角线互相平分
8.(4分)在一次为某位身患重病的小朋友募捐过程中,某年级有50师生通过微信平台奉献了爱心.小东对他们的捐款金额进行统计,并绘制了如下统计图.师生捐款金额的平均数和众数分别是( )
A.20,20 B.32.4,30 C.32.4,20 D.20,30
9.(4分)估算﹣1的值( )
A.在2和3之间 B.在3和4之间
C.在4和5之间 D.在5和6之间
10.(4分)如图是一个运算程序的示意图,若第一次输入x的值为9,则第2022次输出的结果为( )
A.1 B.3 C.9 D.无法确定
11.(4分)自驾游已成为自助旅游的一种时尚.“五一”放假期间华华一家人自驾去梵净山游玩,如图描述了华华爸爸驾驶的汽车在一段时间内路程s(千米)与时间t(小时)的函数关系,下列说法中正确的是( )
A.汽车行驶的平均速度为60千米/时
B.汽车在0~1小时的速度是60千米/时
C.汽车在2~3小时的速度比0~0.5小时的速度快
D.汽车从0.5小时到1.5小时的速度是80千米/时
12.(4分)如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )
A.30° B.45° C.60° D.55°
二、填空题(本大题共4个小题,每小题4分,共16分)在每小题中,请将你认为正确的答案填在答题卡相应位置的横线上。
13.(4分)把直线y=3x向上平移2个单位得到一条新的直线,则这条新直线的解析式为 .
14.(4分)《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架,书中的算法体系至今仍在推动着计算机的发展和应用.
《九章算术》中记载:今有户不知高、广,竿不知长、短.横之不出四尺,从之不出二尺,邪之适出.问户高、广、邪各几何?
译文是:今有门,不知其高、宽,有竿,不知其长、短.横放,竿比门宽长出4尺;竖放,竿比门高长出2尺;斜放,竿与门对角线恰好相等.问门高、宽、对角线长分别是多少?若设门对角线长为x尺,则可列方程为 .
15.(4分)如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则BD的长为 .
16.(4分)精益宏达公司为进一步扩大影响力,提升市场知名度,准备向某工厂订制10套吉祥物送给顾客.已知一套吉祥物需A,B,C三种配饰品共190个组成,且要求所需A配饰品数量不得超过45个,B配饰品数量恰好是A配饰品数量的3倍,B配饰品数量不得低于A,C两配饰品数量之和.该工厂经过试验,发现工人的制作能力情况是:每个工人每天可制作20个A配饰品或30个B配饰品或10个C配饰品.若该工厂安排一批工人恰好10天能完成此次订制任务,则制作一套这种吉祥物所需B配饰品的数量是 个.
三、解答题(本大题2个小题,每小题8分,共16分)解答时每小题必须给出必要的演算过程或推理步骤,请将解答书写在答题卡中对应的位置上。
17.(8分)计算:
(1);
(2).
18.(8分)如图,在 ABCD中,AB>BC.BE平分∠ABC.
(1)尺规作图:作∠BAD的平分线交CD于点F.(保留作图痕迹,不写作法,不写结论)
(2)在(1)所作的图形中,BE与AF交于点P,求证:△ABP为直角三角形.
四、解答题(本大题7个小题,每小题10分,共70分)解答时每小题必须给出必要的演算过程或推理步骤,请将解答书写在答题卡中对应的位置上。
19.(10分)某校要从旺旺和墩墩两名同学中挑选一人参加全县生物实验竞赛,在最近的5次选拔测试中,他俩的成绩(单位:分)如下表:
第1次 第2次 第3次 第4次 第5次
旺旺成绩 65 75 100 85 75
墩墩成绩 70 90 80 80 80
根据上表解答下列问题:
(1)完成下表:
姓名 平均成绩/分 中位数/分 众数/分 方差
旺旺 80 75 75 140
墩墩
(2)在这5次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则旺旺、墩墩在5次测试中的优秀率各是多少;
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获一等奖,那么你认为应选谁参加比赛比较合适?说明你的理由.
20.(10分)已知y+4与x成正比例,且x=3时,y=2.
(1)求出y与x之间的函数关系式;
(2)在所给的直角坐标系(如图)中画出函数的图象;
(3)直接写出当﹣4≤y≤0时,自变量x的取值范围.
21.(10分)如图,在4×3正方形网格中,每个小正方形的边长都是1
(1)分别求出线段AB、CD的长度;
(2)在图中画线段EF、使得EF的长为,以AB、CD、EF三条线段能否构成直角三角形,并说明理由.
22.(10分)“每天一杯纯牛奶”已经成为人们生活的健康时尚,市场上对牛奶的需求越发增大.某乳品公司每月均需通过“飞快”快递公司向A地输送一批牛奶.“飞快”公司给出三种运费方案,具体如下:
方案一:每千克运费0.45元,按实际运输重量结算;
方案二:每月收取600元管理费用,再每千克运费0.15元;
方案三:每月收取1350元包干,不限运输重量.
设该公司每月运输牛奶x千克,选择方案一时,运费为y1元,选择方案二时,运费为y2元,选择方案三时,运费为y3元.
(1)请直接写出y1,y2,y3与x之间的关系式;
(2)在同一个坐标系中,若三种方案对应的函数图象如图所示,请求出点C,D,E的坐标,并直接写出如何选择方案更合算.
23.(10分)如图,在△ABC中,点D、E、F分别是边AC、AB、BC的中点,且.
(1)求证:四边形BFDE为矩形;
(2)若∠C=30°,BD=3,写出矩形BFDE的周长.
24.(10分)定义:对于三位自然数n=100a+10b+c(a≥1,b≤9,c≤9且a,b,c均为整数),若a+7=b+c,则称这样的三位自然数为“偶伴数”,并规定.例如:346是“偶伴数”,因为346,3+7=4+6,所以346是“偶伴数”,且,235不是“偶伴数”,因为2+7≠3+5,所以235不是“偶伴页.
(1)判断593与437是不是“偶伴数”,并说明理由;
(2)求大于600并能被7整除的所有“偶伴数”,并求出对应的所有F(n)的值.
25.(10分)已知,平行四边形ABCD中,连接BD,BD=BC,过点C作CE⊥BD,垂足为E,延长CE与AD相交于点F.
(1)如图1,若BE=4,DE=2.求线段AB的长;
(2)如图2,若∠CBD=45°,过点F作FG⊥AB于点G,连接BF、EG.求证:.
2021-2022学年重庆市秀山县八年级(下)期末数学试卷
参考答案
一、单选题:(本大题12个小题,每小题4分,共48分)请将答题卡上对应题号的正确答案标号涂黑。
1.(4分)函数y=中,自变量x的取值范围是( )
A.x>1 B.x≥1 C.x<1 D.x≤1
选:B.
2.(4分)下列各式中,运算正确的是( )
A. B. C. D.2﹣
选:B.
3.(4分)下表记录了甲、乙、丙、丁四名同学最近几次数学考试成绩的平均数与方差:要选择一名成绩好且发挥稳定的同学参加数学竞赛,应该选择( )
甲 乙 丙 丁
平均数(分) 92 95 95 92
方差 3.6 3.6 7.4 8.1
A.甲 B.乙 C.丙 D.丁
选:B.
4.(4分)下列关于x的函数中,是正比例函数的为( )
A.y=x2 B.y= C.y= D.y=
选:C.
5.(4分)下列四组线段中,不能作为直角三角形三条边的是( )
A.3,4,5 B.2,2,2 C.2,5,6 D.5,12,13
选:C.
6.(4分)为了研究特殊四边形,李老师制作了这样一个教具(如图1):用钉子将四根木条钉成一个平行四边形框架ABCD,并在A与C、B与D两点之间分别用一根橡皮筋拉直固定.课上,李老师右手拿住木条BC,用左手向右推动框架至AB⊥BC(如图2).观察所得到的四边形,下列判断正确的是( )
A.∠BCA=45° B.BD的长度变小
C.AC=BD D.AC⊥BD
选:C.
7.(4分)在下列图形性质中,平行四边形不一定具备的是( )
A.对角线相等 B.两组对边分别平行
C.两组对边分别相等 D.对角线互相平分
选:A.
8.(4分)在一次为某位身患重病的小朋友募捐过程中,某年级有50师生通过微信平台奉献了爱心.小东对他们的捐款金额进行统计,并绘制了如下统计图.师生捐款金额的平均数和众数分别是( )
A.20,20 B.32.4,30 C.32.4,20 D.20,30
选:B.
9.(4分)估算﹣1的值( )
A.在2和3之间 B.在3和4之间
C.在4和5之间 D.在5和6之间
选:A.
10.(4分)如图是一个运算程序的示意图,若第一次输入x的值为9,则第2022次输出的结果为( )
A.1 B.3 C.9 D.无法确定
选:C.
11.(4分)自驾游已成为自助旅游的一种时尚.“五一”放假期间华华一家人自驾去梵净山游玩,如图描述了华华爸爸驾驶的汽车在一段时间内路程s(千米)与时间t(小时)的函数关系,下列说法中正确的是( )
A.汽车行驶的平均速度为60千米/时
B.汽车在0~1小时的速度是60千米/时
C.汽车在2~3小时的速度比0~0.5小时的速度快
D.汽车从0.5小时到1.5小时的速度是80千米/时
选:D.
12.(4分)如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )
A.30° B.45° C.60° D.55°
选:B.
二、填空题(本大题共4个小题,每小题4分,共16分)在每小题中,请将你认为正确的答案填在答题卡相应位置的横线上。
13.(4分)把直线y=3x向上平移2个单位得到一条新的直线,则这条新直线的解析式为 y=3x+2 .
14.(4分)《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架,书中的算法体系至今仍在推动着计算机的发展和应用.
《九章算术》中记载:今有户不知高、广,竿不知长、短.横之不出四尺,从之不出二尺,邪之适出.问户高、广、邪各几何?
译文是:今有门,不知其高、宽,有竿,不知其长、短.横放,竿比门宽长出4尺;竖放,竿比门高长出2尺;斜放,竿与门对角线恰好相等.问门高、宽、对角线长分别是多少?若设门对角线长为x尺,则可列方程为 x2=(x﹣4)2+(x﹣2)2 .
15.(4分)如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则BD的长为 4 .
16.(4分)精益宏达公司为进一步扩大影响力,提升市场知名度,准备向某工厂订制10套吉祥物送给顾客.已知一套吉祥物需A,B,C三种配饰品共190个组成,且要求所需A配饰品数量不得超过45个,B配饰品数量恰好是A配饰品数量的3倍,B配饰品数量不得低于A,C两配饰品数量之和.该工厂经过试验,发现工人的制作能力情况是:每个工人每天可制作20个A配饰品或30个B配饰品或10个C配饰品.若该工厂安排一批工人恰好10天能完成此次订制任务,则制作一套这种吉祥物所需B配饰品的数量是 120 个.
三、解答题(本大题2个小题,每小题8分,共16分)解答时每小题必须给出必要的演算过程或推理步骤,请将解答书写在答题卡中对应的位置上。
17.(8分)计算:
(1);
(2).
【解答】解:(1)
=﹣()2+()2
=4﹣7+3
=0;
(2)
=1+9﹣(﹣1)+3
=10﹣+1+3
=11+2.
18.(8分)如图,在 ABCD中,AB>BC.BE平分∠ABC.
(1)尺规作图:作∠BAD的平分线交CD于点F.(保留作图痕迹,不写作法,不写结论)
(2)在(1)所作的图形中,BE与AF交于点P,求证:△ABP为直角三角形.
【解答】(1)解:如图,AF为所作;
(2)证明:∵四边形ABCD为平行四边形,
∴∠BAD+∠ABC=180°,
∵AF平分∠BAD,BE平分∠ABC,
∴∠PAB=∠BAD,∠PBA=∠ABC,
∴∠PAB+∠PBA=×180°=90°,
∴∠APB=90°,
∴△ABP为直角三角形.
四、解答题(本大题7个小题,每小题10分,共70分)解答时每小题必须给出必要的演算过程或推理步骤,请将解答书写在答题卡中对应的位置上。
19.(10分)某校要从旺旺和墩墩两名同学中挑选一人参加全县生物实验竞赛,在最近的5次选拔测试中,他俩的成绩(单位:分)如下表:
第1次 第2次 第3次 第4次 第5次
旺旺成绩 65 75 100 85 75
墩墩成绩 70 90 80 80 80
根据上表解答下列问题:
(1)完成下表:
姓名 平均成绩/分 中位数/分 众数/分 方差
旺旺 80 75 75 140
墩墩 80 80 80 40
(2)在这5次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则旺旺、墩墩在5次测试中的优秀率各是多少;
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获一等奖,那么你认为应选谁参加比赛比较合适?说明你的理由.
【解答】解:(1)墩墩的成绩:70、80、80、80、90,
∴平均成绩为:(70+80+80+80+90)÷5=80(分),
众数为:80分,中位数是80分;
方差为:[(70﹣80)2+(80﹣80)2+(80﹣80)2+(80﹣80)2+(90﹣80)2]÷5=40,
姓名 平均成绩/分 中位数/分 众数/分 方差
旺旺 80 75 75 140
墩墩 80 80 80 40
故答案为:80,80,80,40;
(2)∵旺旺的方差是140,墩墩的方差是40,而40<140,
∴墩墩成绩较稳定;
旺旺的优秀率为×100%=40%,墩墩的优秀率为×100%=80%;
(3)选墩墩参加比赛比较合适,理由:
虽然两人的平均数相同,但墩墩的成绩比旺旺稳定,且优秀率比旺旺的高,因此选墩墩参加比赛比较合适.
20.(10分)已知y+4与x成正比例,且x=3时,y=2.
(1)求出y与x之间的函数关系式;
(2)在所给的直角坐标系(如图)中画出函数的图象;
(3)直接写出当﹣4≤y≤0时,自变量x的取值范围.
【解答】解:(1)∵y+4与x成正比例,
∴设y+4=kx(k≠0),
∵当x=3时,y=2,
∴2+4=3k,
解得k=2,
∴y+4=2x,
函数关系式为:y=2x﹣4;
(2)当x=0时,y=﹣4,
当y=0时,2x﹣4=0,解得x=2,
所以,函数图象经过点(0,﹣4),(2,0),
函数图象如图:
(3)由图象得:当﹣4≤y≤0时,自变量x的取值范围是:0≤x≤2.
21.(10分)如图,在4×3正方形网格中,每个小正方形的边长都是1
(1)分别求出线段AB、CD的长度;
(2)在图中画线段EF、使得EF的长为,以AB、CD、EF三条线段能否构成直角三角形,并说明理由.
【解答】解:(1)AB==;CD==2.
(2)如图,EF==,
∵CD2+EF2=8+5=13,AB2=13,
∴CD2+EF2=AB2,
∴以AB、CD、EF三条线可以组成直角三角形.
22.(10分)“每天一杯纯牛奶”已经成为人们生活的健康时尚,市场上对牛奶的需求越发增大.某乳品公司每月均需通过“飞快”快递公司向A地输送一批牛奶.“飞快”公司给出三种运费方案,具体如下:
方案一:每千克运费0.45元,按实际运输重量结算;
方案二:每月收取600元管理费用,再每千克运费0.15元;
方案三:每月收取1350元包干,不限运输重量.
设该公司每月运输牛奶x千克,选择方案一时,运费为y1元,选择方案二时,运费为y2元,选择方案三时,运费为y3元.
(1)请直接写出y1,y2,y3与x之间的关系式;
(2)在同一个坐标系中,若三种方案对应的函数图象如图所示,请求出点C,D,E的坐标,并直接写出如何选择方案更合算.
【解答】解:(1)由题意得y1=0.45x;y2=0.15x+600;y3=1350;
(2)解方程0.45x=0.15x+600,得x=2000,
0.45×2000=900,
故点C的坐标为(2000,900);
解方程0.45x=1350,得x=3000,
故点D的坐标为(3000,1350);
解方程0.15x+600=1350,得x=5000,
故点E的坐标为(5000,1350);
由图象可知,当0<x≤2000时,采用方案一更合算;当450<x≤5000时,采用方案二更合算;当x>5000时,采用方案三更合算.
23.(10分)如图,在△ABC中,点D、E、F分别是边AC、AB、BC的中点,且.
(1)求证:四边形BFDE为矩形;
(2)若∠C=30°,BD=3,写出矩形BFDE的周长.
【解答】(1)证明:∵点D、E、F分别是边AC、AB、BC的中点,
∴DE、DF是△ABC的中位线,
∴DE∥BC,DF∥AB,
∴四边形BFDE是平行四边形,
∵D是AC的中点,且,
∴△ABC是直角三角形,且∠ABC=90°,
∴平行四边形BFDE为矩形;
(2)解:由(1)可知,四边形BFDE为矩形,
∴BE=DF,BF=DE,∠DFB=90°,
∵BD=AC=CD,
∴∠DBF=∠C=30°,
∴DF=BD=,
∴BF===,
∴矩形BFDE的周长=2(DF+BF)=3+3.
24.(10分)定义:对于三位自然数n=100a+10b+c(a≥1,b≤9,c≤9且a,b,c均为整数),若a+7=b+c,则称这样的三位自然数为“偶伴数”,并规定.例如:346是“偶伴数”,因为346,3+7=4+6,所以346是“偶伴数”,且,235不是“偶伴数”,因为2+7≠3+5,所以235不是“偶伴页.
(1)判断593与437是不是“偶伴数”,并说明理由;
(2)求大于600并能被7整除的所有“偶伴数”,并求出对应的所有F(n)的值.
【解答】解:(1)∵5+7=3+9,4+7≠3+7
∴593是偶伴数,437不是偶伴数;
(2)①当a=6时,则b+c=13,且能被7整除,
偶伴数为658,此时
F(658)=;
②当a=7时,则b+c=14,且能被7整除,
偶伴数为777,此时
F(777)=;
③当a=8,则b+c=15,且能被7整除,
偶伴数为896,此时
F(896)=;
④当a=9,则b+c=16,且能被7整除,
此时不存在满足条件的偶伴数,
综上分析,大于600并能被7整除的所有偶伴数是658或777或896,对应的F(n)的值分别是或或.
25.(10分)已知,平行四边形ABCD中,连接BD,BD=BC,过点C作CE⊥BD,垂足为E,延长CE与AD相交于点F.
(1)如图1,若BE=4,DE=2.求线段AB的长;
(2)如图2,若∠CBD=45°,过点F作FG⊥AB于点G,连接BF、EG.求证:.
【解答】(1)解:∵BE=4,DE=2,
∴BD=BE+DE=6,
∵BD=BC,
∴BC=6,
∵CE⊥BD,
∴∠BEC=∠DEC=90°,
在Rt△BEC中,由勾股定理得CE==2,
在Rt△DEC中,由勾股定理得CD==2,
∵四边形ABCD是平行四边形,
∴AB=CD=2;
(2)证明:∵CE⊥AD,
∴∠BEC=∠CED=90°,
∵∠CBE=45°,
∴△BCE是等腰直角三角形,
∴∠BCE=45°,CE=BE,
∵BC∥AD,
∴∠BDF=45°,∠ACC+∠DCB=180°,
设∠DCE=x,
∴∠BCD=45°+x,
∵BC=BD,
∴∠BDC=∠BCE=45°+x,
∵∠ECD+∠EDC=90°,
∴x+45°+x=90°,
∴x=22.5°,
∴∠ECD=22.5°,∠BDC=67.5°,
∵∠BCF=∠ADE=∠DFE=∠CBE=45°,
∴DE=EF,
∴CF=BD,
在△CFD和△BDF中,
,
∴△CFD≌△BDF(SAS),
∴∠DBF=∠DCF=22.5°,
∵AB∥CD,
∴∠ABC=180°﹣∠BCD=180°﹣67.5°=112.5°,
∴∠ABD=67.5°,
∵FG⊥AB,
∴∠BGF=∠AEF=90°,
∴∠EGF=∠EAF=22.5°,
∴∠AGE=67.5°,
∵∠CAD=∠ACB=67.5°,
∴∠EAG=∠AGE,
∴AE=GE,
∵AC=AB=AE,
∴BE+EC=AE+EC=AC=EG.
同课章节目录
