2023-2024学年吉林省长春市吉大附中实验学校高一(下)期末数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年吉林省长春市吉大附中实验学校高一(下)期末数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 179.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 18:39:17 | ||
图片预览



文档简介
2023-2024学年吉林省长春市吉大附中实验学校高一(下)期末数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.样本数据,,,,,,,的第百分位数次为( )
A. B. C. D.
2.已知向量,,其中,,且,则向量与的夹角是( )
A. B. C. D.
3.从一批产品既有正品也有次品中随机抽取三件产品,设事件“三件产品全不是次品”,事件“三件产品全是次品”,事件“三件产品有次品,但不全是次品”,则下列结论中不正确的是( )
A. 与互斥 B. 与互斥
C. A、、两两互斥 D. 与对立
4.已知,是两条不同直线,,是两个不同平面,则( )
A. ,,则
B. ,,则
C. ,,,,则
D. ,,,,,则
5.已知正四棱台的上、下底面边长分别为和,且,则该棱台的体积为( )
A. B. C. D.
6.在中,角,,的对边分别为,,已知三个向量,,共线,则的形状为( )
A. 等边三角形 B. 钝角三角形.
C. 有一个角是的直角三角形 D. 等腰直角三角形
7.一个电路如图所示,,,,,,为个开关,其闭合的概率都是,且是相互独立的,则灯亮的概率是( )
A. B.
C. D.
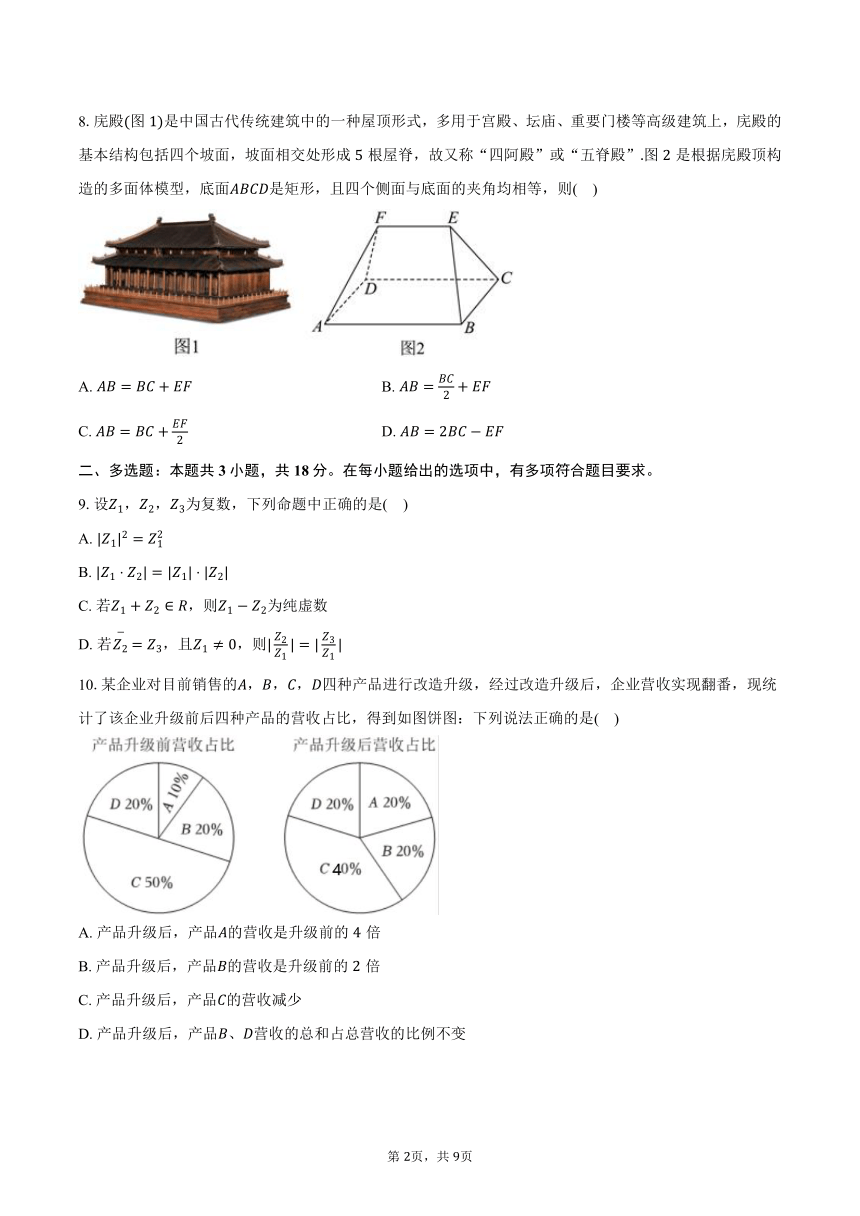
8.庑殿图是中国古代传统建筑中的一种屋顶形式,多用于宫殿、坛庙、重要门楼等高级建筑上,庑殿的基本结构包括四个坡面,坡面相交处形成根屋脊,故又称“四阿殿”或“五脊殿”图是根据庑殿顶构造的多面体模型,底面是矩形,且四个侧面与底面的夹角均相等,则( )
A. B.
C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.设,,为复数,下列命题中正确的是( )
A.
B.
C. 若,则为纯虚数
D. 若,且,则
10.某企业对目前销售的,,,四种产品进行改造升级,经过改造升级后,企业营收实现翻番,现统计了该企业升级前后四种产品的营收占比,得到如图饼图:下列说法正确的是( )
A. 产品升级后,产品的营收是升级前的倍
B. 产品升级后,产品的营收是升级前的倍
C. 产品升级后,产品的营收减少
D. 产品升级后,产品、营收的总和占总营收的比例不变
11.如图,在社会实践活动中,李明同学设计了一款很“萌”的圆台形台灯,台灯内装有两个相切且球心均在圆台的轴上的球形灯泡,上、下两灯泡的球面分别与圆台的上、下底面相切,且都与圆台的侧面相切,若上、下两球形灯泡的半径分别为和,则( )
A. 圆台形台灯的母线所在直线与下底面所成角的大小为
B. 圆台形台灯的母线长为
C. 圆台形的上、下底面半径之积为
D. 圆台形台灯的侧面积大于
三、填空题:本题共3小题,每小题5分,共15分。
12.若一组数据,,,的中位数为,方差为,则另一组数据,,,的中位数为______,方差为______.
13.在矩形中,,,点在对角线上,点在边上,且,,则 ______.
14.非直角的内角,,的对边分别为,,,若,则 ______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
如图,边长为的正方形中,点,分别为,的中点将,,分别沿,,折起,使,,三点重合于点.
求证:;
求三棱锥的体积.
16.本小题分
如图,在平面四边形中,,.
Ⅰ若,,求的值;
Ⅱ若,,求四边形的面积.
17.本小题分
第届亚运会将于年月日至月日在杭州举行,而亚运会志愿者的服务工作是举办一届成功的亚运会的重要保障为配合亚运会志愿者选拔,某高校举行了志愿者选拔面试,面试成绩满分分,现随机抽取了名候选者的面试成绩,绘制成如图频率分布直方图.
求的值,并估计这名候选者面试成绩平均值,众数,中位数;同一组中的数据用该组区间的中点值作代表,中位数精确到
乒乓球项目场地志愿服务需要名志愿者,有名男生和名女生通过该项志愿服务选拔,需要通过抽签的方式决定最终的人选,现将张写有“中签”和张写有“未中签”字样的字条随机分配给每一位候选人,求中签者中男生比女生多的概率.
18.本小题分
如图,四棱锥与三棱锥构成了一个组合体,其中在线段上,且、、三点共线四边形是边长为的正方形,且,为棱中点,且平面.
证明:平面;
证明:平面;
求平面与平面所成角的大小.
19.本小题分
为了建设书香校园,营造良好的读书氛围,学校开展“送书券”活动该活动由三个游戏组成,每个游戏各玩一次且结果互不影响连胜两个游戏可以获得一张书券,迬胜三个游戏可以获得两张书券游戏规则如下表:
游戏一 游戏二 游戏三
箱子中球的
颜色和数量 大小质地完全相同的红球个,白球个
红球编号为“,,”,白球编号为“,”
取球规则 取出一个球 有放回地依次取出两个球 不放回地依次取出两个球
获胜规则 取到白球获胜 取到两个白球获胜 编号之和为获胜
分别求出游戏一,游戏二的获胜概率;
一名同学先玩了游戏一,试问为何值时,接下来先玩游戏三比先玩游戏二获得书券的概率更大.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.证明:因为在正方形中,,,
折叠后即有,,
又,,平面,
所以平面,而平面,
故;
解:由题意知,,
所以,
所以.
16.解:Ⅰ在中,由余弦定理,
可得,
则,
在中,由正弦定理,
可得,即;
Ⅱ在中,,
在中,,
联立,可得,又,
解得,,又,,
,,
故四边形的面积.
17.解:由频率分布直方图可知,解得,
,
众数为,
因为前组的频率和为,前组的频率和为,
所以中位数在第组,设中位数为,
则,解得,
所以中位数为.
记名男生分别为,,,记名女生分别为,,则所有抽签的情况有:
未中签,中签;未中签,中签;未中签,中签;
未中签,中签;未中签,中签;未中签,中签;
未中签,中签;未中签,中签;未中签,中签;
未中签,中签,共有种情况,
其中中签者中男生比女生多的有:未中签,中签;未中签,中签;
未中签,中签;未中签,中签;未中签,中签;
未中签,中签;未中签,中签,共种,
所以中签者中男生比女生多的概率为.
18.解:证明:连接,,,
,,
,,
即四边形为平行四边形,则点为的中点,
又为中点,
,
平面,平面,
平面.
证明:平面,,平面,
,,
又,,平面,,
平面,平面,
,
又平面,
,
在中,,
,
,
,
,,平面,
平面.
由,,可得,
又平面,平面,
,,
则平面与平面所成角为,
又点为中点,,
,
在中,,
则,
则平面与平面所成角为.
19.解:由题意知游戏一获胜的概率为,
游戏二总事件数为,获胜的事件数为,
所以游戏二获胜的概率为;
若为,,时则游戏三获胜的事件数为,总事件数为,概率为,
同理为,时游戏三获胜的概率为,为其他数时游戏三获胜的概率为,
若游戏三获胜概率为,当该同学先玩游戏二获得书券的概率为,
先玩游戏三获得书券的概率为,大于先玩游戏二获得书券的概率,
若游戏三获胜概率为,当该同学先玩游戏二获得书券的概率为,
先玩游戏三获得书券的概率为,大于先玩游戏二获得书券的概率,
若游戏三获胜概率为,显然先玩游戏三不可能获得书券,而先玩游戏二获得书券的概率为,
综上,当为,,,,时,接下来先玩游戏三比先玩游戏二获得书券的概率更大.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.样本数据,,,,,,,的第百分位数次为( )
A. B. C. D.
2.已知向量,,其中,,且,则向量与的夹角是( )
A. B. C. D.
3.从一批产品既有正品也有次品中随机抽取三件产品,设事件“三件产品全不是次品”,事件“三件产品全是次品”,事件“三件产品有次品,但不全是次品”,则下列结论中不正确的是( )
A. 与互斥 B. 与互斥
C. A、、两两互斥 D. 与对立
4.已知,是两条不同直线,,是两个不同平面,则( )
A. ,,则
B. ,,则
C. ,,,,则
D. ,,,,,则
5.已知正四棱台的上、下底面边长分别为和,且,则该棱台的体积为( )
A. B. C. D.
6.在中,角,,的对边分别为,,已知三个向量,,共线,则的形状为( )
A. 等边三角形 B. 钝角三角形.
C. 有一个角是的直角三角形 D. 等腰直角三角形
7.一个电路如图所示,,,,,,为个开关,其闭合的概率都是,且是相互独立的,则灯亮的概率是( )
A. B.
C. D.
8.庑殿图是中国古代传统建筑中的一种屋顶形式,多用于宫殿、坛庙、重要门楼等高级建筑上,庑殿的基本结构包括四个坡面,坡面相交处形成根屋脊,故又称“四阿殿”或“五脊殿”图是根据庑殿顶构造的多面体模型,底面是矩形,且四个侧面与底面的夹角均相等,则( )
A. B.
C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.设,,为复数,下列命题中正确的是( )
A.
B.
C. 若,则为纯虚数
D. 若,且,则
10.某企业对目前销售的,,,四种产品进行改造升级,经过改造升级后,企业营收实现翻番,现统计了该企业升级前后四种产品的营收占比,得到如图饼图:下列说法正确的是( )
A. 产品升级后,产品的营收是升级前的倍
B. 产品升级后,产品的营收是升级前的倍
C. 产品升级后,产品的营收减少
D. 产品升级后,产品、营收的总和占总营收的比例不变
11.如图,在社会实践活动中,李明同学设计了一款很“萌”的圆台形台灯,台灯内装有两个相切且球心均在圆台的轴上的球形灯泡,上、下两灯泡的球面分别与圆台的上、下底面相切,且都与圆台的侧面相切,若上、下两球形灯泡的半径分别为和,则( )
A. 圆台形台灯的母线所在直线与下底面所成角的大小为
B. 圆台形台灯的母线长为
C. 圆台形的上、下底面半径之积为
D. 圆台形台灯的侧面积大于
三、填空题:本题共3小题,每小题5分,共15分。
12.若一组数据,,,的中位数为,方差为,则另一组数据,,,的中位数为______,方差为______.
13.在矩形中,,,点在对角线上,点在边上,且,,则 ______.
14.非直角的内角,,的对边分别为,,,若,则 ______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
如图,边长为的正方形中,点,分别为,的中点将,,分别沿,,折起,使,,三点重合于点.
求证:;
求三棱锥的体积.
16.本小题分
如图,在平面四边形中,,.
Ⅰ若,,求的值;
Ⅱ若,,求四边形的面积.
17.本小题分
第届亚运会将于年月日至月日在杭州举行,而亚运会志愿者的服务工作是举办一届成功的亚运会的重要保障为配合亚运会志愿者选拔,某高校举行了志愿者选拔面试,面试成绩满分分,现随机抽取了名候选者的面试成绩,绘制成如图频率分布直方图.
求的值,并估计这名候选者面试成绩平均值,众数,中位数;同一组中的数据用该组区间的中点值作代表,中位数精确到
乒乓球项目场地志愿服务需要名志愿者,有名男生和名女生通过该项志愿服务选拔,需要通过抽签的方式决定最终的人选,现将张写有“中签”和张写有“未中签”字样的字条随机分配给每一位候选人,求中签者中男生比女生多的概率.
18.本小题分
如图,四棱锥与三棱锥构成了一个组合体,其中在线段上,且、、三点共线四边形是边长为的正方形,且,为棱中点,且平面.
证明:平面;
证明:平面;
求平面与平面所成角的大小.
19.本小题分
为了建设书香校园,营造良好的读书氛围,学校开展“送书券”活动该活动由三个游戏组成,每个游戏各玩一次且结果互不影响连胜两个游戏可以获得一张书券,迬胜三个游戏可以获得两张书券游戏规则如下表:
游戏一 游戏二 游戏三
箱子中球的
颜色和数量 大小质地完全相同的红球个,白球个
红球编号为“,,”,白球编号为“,”
取球规则 取出一个球 有放回地依次取出两个球 不放回地依次取出两个球
获胜规则 取到白球获胜 取到两个白球获胜 编号之和为获胜
分别求出游戏一,游戏二的获胜概率;
一名同学先玩了游戏一,试问为何值时,接下来先玩游戏三比先玩游戏二获得书券的概率更大.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.证明:因为在正方形中,,,
折叠后即有,,
又,,平面,
所以平面,而平面,
故;
解:由题意知,,
所以,
所以.
16.解:Ⅰ在中,由余弦定理,
可得,
则,
在中,由正弦定理,
可得,即;
Ⅱ在中,,
在中,,
联立,可得,又,
解得,,又,,
,,
故四边形的面积.
17.解:由频率分布直方图可知,解得,
,
众数为,
因为前组的频率和为,前组的频率和为,
所以中位数在第组,设中位数为,
则,解得,
所以中位数为.
记名男生分别为,,,记名女生分别为,,则所有抽签的情况有:
未中签,中签;未中签,中签;未中签,中签;
未中签,中签;未中签,中签;未中签,中签;
未中签,中签;未中签,中签;未中签,中签;
未中签,中签,共有种情况,
其中中签者中男生比女生多的有:未中签,中签;未中签,中签;
未中签,中签;未中签,中签;未中签,中签;
未中签,中签;未中签,中签,共种,
所以中签者中男生比女生多的概率为.
18.解:证明:连接,,,
,,
,,
即四边形为平行四边形,则点为的中点,
又为中点,
,
平面,平面,
平面.
证明:平面,,平面,
,,
又,,平面,,
平面,平面,
,
又平面,
,
在中,,
,
,
,
,,平面,
平面.
由,,可得,
又平面,平面,
,,
则平面与平面所成角为,
又点为中点,,
,
在中,,
则,
则平面与平面所成角为.
19.解:由题意知游戏一获胜的概率为,
游戏二总事件数为,获胜的事件数为,
所以游戏二获胜的概率为;
若为,,时则游戏三获胜的事件数为,总事件数为,概率为,
同理为,时游戏三获胜的概率为,为其他数时游戏三获胜的概率为,
若游戏三获胜概率为,当该同学先玩游戏二获得书券的概率为,
先玩游戏三获得书券的概率为,大于先玩游戏二获得书券的概率,
若游戏三获胜概率为,当该同学先玩游戏二获得书券的概率为,
先玩游戏三获得书券的概率为,大于先玩游戏二获得书券的概率,
若游戏三获胜概率为,显然先玩游戏三不可能获得书券,而先玩游戏二获得书券的概率为,
综上,当为,,,,时,接下来先玩游戏三比先玩游戏二获得书券的概率更大.
第1页,共1页
同课章节目录
