甘肃省酒泉市2023-2024学年高一下学期7月期末考试数学试卷(含解析)
文档属性
| 名称 | 甘肃省酒泉市2023-2024学年高一下学期7月期末考试数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 21:29:51 | ||
图片预览




文档简介
甘肃省酒泉市2023-2024学年高一下学期7月期末考试数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.某省为全运会选拔跳水运动员,对某运动员进行测试,在运动员跳完一个动作之后由7名裁判打分,统计结果为平均分9.5分,方差为a,为体现公平,裁判委员会决定去掉一个最高分10分,一个最低分9分,则( )
A.平均分变大,方差变大 B.平均分变小,方差变小
C.平均分变小,方差变大 D.平均分不变,方差变小
2.已知i是虚数单位,则复数( )
A.-1 B.i C. D.1
3.已知向量,,若,则( )
A. B. C. D.6
4.设α是空间中的一个平面,l,m,n是三条不同的直线,则( )
A.若,,,,则
B.若,,,则
C.若,,,则
D.若,,,则
5.三人被邀请参加一个晚会,若晚会必须有人去,去几人自行决定,则恰有一人参加晚会的概率为( )
A. B. C. D.
6.若正方体的内切球的表面积为,则此正方体最多可容纳半径为1的小球的个数为( )
A.7个 B.8个 C.9个 D.10个
7.已知,则( )
A. B. C. D.
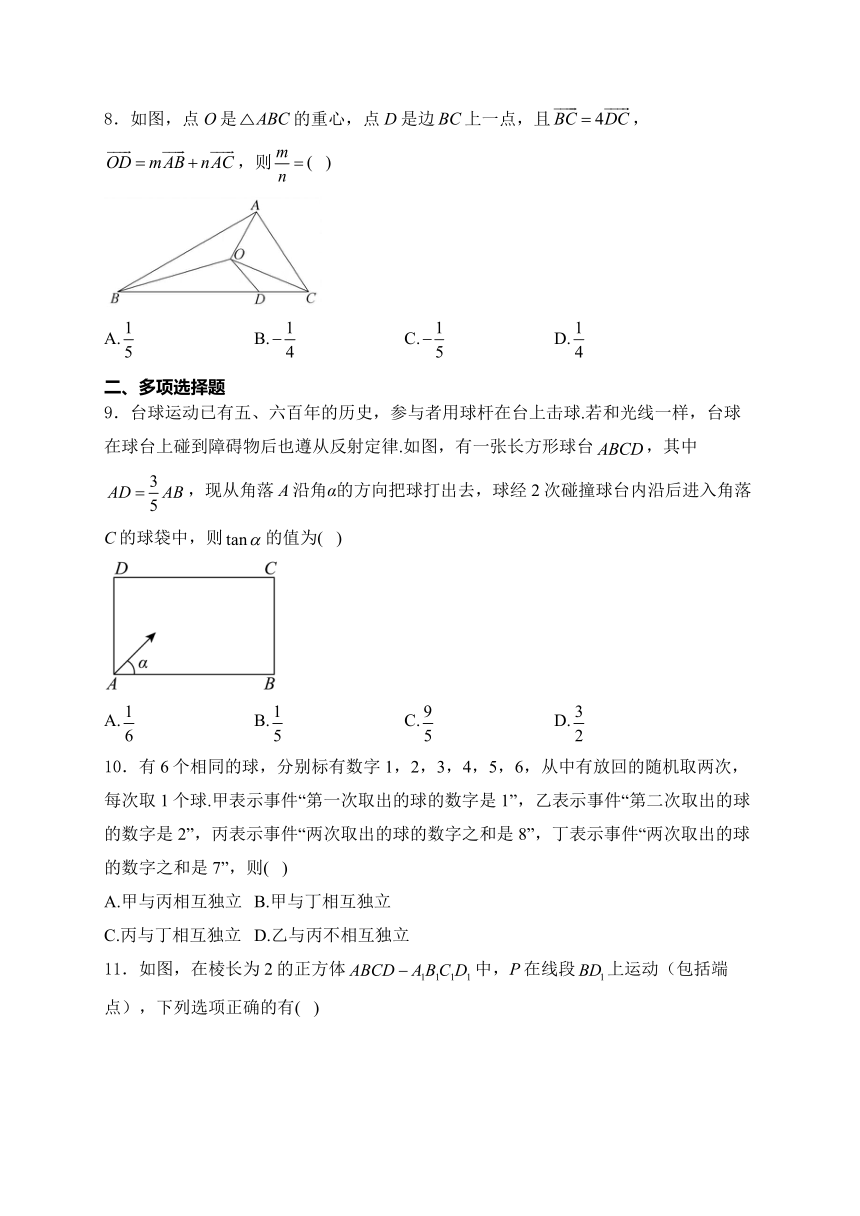
8.如图,点O是的重心,点D是边上一点,且,,则( )
A. B. C. D.
二、多项选择题
9.台球运动已有五、六百年的历史,参与者用球杆在台上击球.若和光线一样,台球在球台上碰到障碍物后也遵从反射定律.如图,有一张长方形球台,其中,现从角落A沿角α的方向把球打出去,球经2次碰撞球台内沿后进入角落C的球袋中,则的值为( )
A. B. C. D.
10.有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回的随机取两次,每次取1个球.甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”,丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7”,则( )
A.甲与丙相互独立 B.甲与丁相互独立
C.丙与丁相互独立 D.乙与丙不相互独立
11.如图,在棱长为2的正方体中,P在线段上运动(包括端点),下列选项正确的有( )
A.
B.
C.直线与平面所成角的最大值是
D.的最小值为
三、填空题
12.已知复数z的模为2,则的最大值为________.
13.某科研攻关项目中遇到一个问题,请了甲、乙两位专家单独解决此问题,若甲、乙能解决此问题的概率分别为m,n,则此问题被解决的概率为________.
14.滕王阁,江南三大名楼之一,因初唐诗人王勃所作《滕王阁序》中的“落霞与孤鹜齐飞,秋水共长天一色”而名传千古,流芳后世.如图,在滕王阁旁地面上共线的三点A,B,C处测得阁顶端点P的仰角分别为,,.且米,则滕王阁高度________米.
四、解答题
15.已知,,与的夹角是.
(1)求的值及的值;
(2)当k为何值时,?
16.本学期初,某校对全校高一学生进行数学测试(满分100),并从中随机抽取了100名学生的成绩,以此为样本,分,,,,五组,得到如图所示频率分布直方图.
(1)求a的值,并估计该校高一学生数学成绩的平均数和分位数;
(2)为进一步了解学困生的学习情况,从上述数学成绩低于70分的学生中,分层抽样抽出6人,再从6人中任取2人,求此2人分数都在的概率.
17.(1)叙述并证明平面与平面平行的性质定理;
(2)设,是两个不同的平面,m,n是平面,之外的两条不同直线,给出四个论断:①;②;③;④.以其中三个论断作为条件,余下一个作为结论,写出一个正确的命题,并证明.
18.已知向量,,函数.
(1)若,,求的值;
(2)若,,,,求的值;
(3)设中,内角A,B,C所对的边分别为a,b,c,已知,且锐角B满足,求的取值范围.
19.如图,在六面体中,,正方形的边长为2,,,.
(1)证明:平面平面;
(2)求直线EF与平面所成角的正切值;
(3)求平面与平面所成二面角的余弦值;
(4)求多面体的体积.
参考答案
1.答案:D
解析:设7个打分中除了一个最高分10分和一个最低分9分之外的数据为,,,,,
因为,
故可得,
则去掉一个最高分10分和一个最低分9分之后的平均分为;
因为去掉一个最高分和最低分后,数据更加集中,故方差变小.
故选:D.
2.答案:A
解析:.
故选:A
3.答案:A
解析:已知向量,,,
所以,解得.
故选:A.
4.答案:B
解析:对于选项A,如图1,当,满足,,,,时,l与可以斜交,故选项A错误,
对于选项B,因为,,所以,因为,则由线面垂直的判定定理得,故选项B正确,
对于选项C,因为,,所以,因为,所以,故选项C错误,
对于选项D,若,,,则l与m可以相交、平行或异面,如图2,满足,,,而l与m异面,故选项D错误,
故选:B.
5.答案:B
解析:设三人为A,B,C,则参加晚会的情况有A,B,C,AB,AC,BC,ABC,共7种情况,其中恰有一人参加晚会的情况有3种,故所求的概率为.
6.答案:B
解析:设正方体的棱长为a,则其内切球的直径为a,
由题意,解得,即正方体的棱长为4,半径为1的两个球的直径和为4,
故正方体内最多可以放8个半径为1的球.
故选:B
7.答案:B
解析:展开得,
两边同时平方有,
即,解得,
故选:B.
8.答案:C
解析:如图所示,延长交于E,
由已知O为的重心,则点E为的中点,可得,且,
又由,可得D是的四等分点,
则,
因为,所以,,所以.
故选:C.
9.答案:BC
解析:第一种情况:现从角落A沿角的方向把球打出去,球先接触边,反射情况如下:
,,由反射的性质,得,关于对称,,关于对称,
即G,E为的三等分点,因此,C正确;
第二种情况:现从角落A沿角的方向把球打出去,球先接触边,反射情况如下:
,,由反射的性质,得,关于对称,,关于对称,
即G,F为的三等分点,因此,B正确.
故选:BC
10.答案:BD
解析:两次取出的球的数字之和为8,有,,,,,共5种情况,
所以;两次取出的球的数字之和为7,有,,,,,,共6种情况,
所以;;
对于A,,故甲与丙不相互独立,错误;
对于B,,故甲与丁相互独立,正确;
对于C,,故丙与丁不相互独立,错误.
对于D,,故乙与丙不相互独立,正确;
故选:BD.
11.答案:ACD
解析:对于选项A,由正方体性质,易得,,
因为,平面,
所以平面.
因为平面,所以,故A正确;
对于选项B,当P与B重合,则此时与夹角为,故B错误;
对于选项C,如图连接交于H,
因为平面,平面,所以.
因为,,平面,
所以平面,即平面,
所以为直线与平面所成角,所以.
所以当最小时最大,即时,最小.
由,可得,
此时,故的最大值为,
直线与平面所成角的最大值是,故C正确;
对于选项D,如图,将平面与平面沿翻折到同一个平面内
由题意,,,,,,
从而,,故为平行四边形.
又,故为矩形.
从而当P为与交点时,最小,此时,故D正确.
故选:ACD.
12.答案:3
解析:复数z的模为2,表示复数z在复平面内对应的点Z到原点O的距离为2,
则点Z的轨迹是以原点O为圆心,2为半径的圆,
而是圆O上的点到点的距离,
所以.
故答案为:3
13.答案:
解析:记事件“甲专家独立解决”,事件“乙专家独立解决”,
则,,而A,B相互独立,即,
所以,即问题被解决的概率为.
故答案为:
14.答案:
解析:设,因为,,,
所以,,,.
在中,,
即①.,
在中,,
即②,
因为,
所以①②两式相加可得:,解得:,
则,
故答案为:.
15.答案:(1),;
(2).
解析:(1),,与的夹角是,
,
;
(2)由题意,,
即,
解得,
即时,.
16.答案:(1),平均数75.5,分位数88
(2)
解析:(1)由,
解得;
该校高一学生数学成绩的平均数为.
前3组的频率和为,
所以分位数为;
(2)分层抽样抽取的6人中,的有人,记为1,2,
的有人,记为3,4,5,6,
从6人中任取2人,基本事件有12,13,14,15,16,23,24,25,26,34,35,36,45,46,56,共15种,
其中2人分数都在的有34,35,36,45,46,56共6种,
所以从6人中任取2人,分数都在的概率为.
17.答案:(1)答案见解析;
(2)答案见解析
解析:(1)两个平面平行的性质定理:两个平面平行,如果另一个平面与这两个平面相交,那么两条交线平行.
已知:如图,已知,,,求证:.
证明:因为,所以与没有公共点,
又,,所以,,
所以a与b没有公共点,
又,,
;
(2)命题一:若,,,则(②③④①).
证明:过平面和平面外一点P,作,交于A,作,交于B,
则,,,
显然与不平行,设,则、,所以,,
因为,平面,所以平面,
延展平面交l于点M,连接,,平面,
所以,,
则是二面角的一个平面角,
因为,,所以,同理有,
又,所以四边形为矩形,则,
则平面和平面形成的二面角的平面角直二面角,故,
命题二:若,,,则(①③④②).
证明:因为,,,
设,在平面内作直线,根据面面垂直的性质定理可得,
又因为,所以,
因为,,所以,所以.
18.答案:(1);
(2);
(3)
解析:(1)依题意,,
由,得,由,得,则,
则.
(2)由,得,由,得,
则,
由,,得,
则
由,得,
所以的值为.
(3)由,得,而,即,解得,即,则,设,,,,
由正弦定理得,则,,
于是,
所以的取值范围是.
19.答案:(1)证明见解析;
(2);
(3);
(4).
解析:(1)由,平面,平面,得平面,
由正方形,得,又平面,平面,得平面,而,平面,
所以平面平面.
(2)连接,在正方形中,,则,而,,,
即有,,于是,,
而,平面,则平面,由,
得平面,因此在平面内的射影是,
令直线与平面所成的角为,在直角梯形中,,
所以直线EF与平面所成角的正切值为.
(3)延长与的延长线交于点G,连接,则平面平面,
由(2)知,平面,平面,则,
由,,得,取的中点O,连接,,
由,得,而,平面,
则平面,又平面,则,
因此是二面角的平面角,在中,,
而,,则,,
所以平面与平面所成二面角的余弦值是.
(4)由(2)知,平面,而平面,则,又,,平面,于是平面,
四棱锥的体积,
由平面,得三棱锥的体积,
所以多面体的体积.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.某省为全运会选拔跳水运动员,对某运动员进行测试,在运动员跳完一个动作之后由7名裁判打分,统计结果为平均分9.5分,方差为a,为体现公平,裁判委员会决定去掉一个最高分10分,一个最低分9分,则( )
A.平均分变大,方差变大 B.平均分变小,方差变小
C.平均分变小,方差变大 D.平均分不变,方差变小
2.已知i是虚数单位,则复数( )
A.-1 B.i C. D.1
3.已知向量,,若,则( )
A. B. C. D.6
4.设α是空间中的一个平面,l,m,n是三条不同的直线,则( )
A.若,,,,则
B.若,,,则
C.若,,,则
D.若,,,则
5.三人被邀请参加一个晚会,若晚会必须有人去,去几人自行决定,则恰有一人参加晚会的概率为( )
A. B. C. D.
6.若正方体的内切球的表面积为,则此正方体最多可容纳半径为1的小球的个数为( )
A.7个 B.8个 C.9个 D.10个
7.已知,则( )
A. B. C. D.
8.如图,点O是的重心,点D是边上一点,且,,则( )
A. B. C. D.
二、多项选择题
9.台球运动已有五、六百年的历史,参与者用球杆在台上击球.若和光线一样,台球在球台上碰到障碍物后也遵从反射定律.如图,有一张长方形球台,其中,现从角落A沿角α的方向把球打出去,球经2次碰撞球台内沿后进入角落C的球袋中,则的值为( )
A. B. C. D.
10.有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回的随机取两次,每次取1个球.甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”,丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7”,则( )
A.甲与丙相互独立 B.甲与丁相互独立
C.丙与丁相互独立 D.乙与丙不相互独立
11.如图,在棱长为2的正方体中,P在线段上运动(包括端点),下列选项正确的有( )
A.
B.
C.直线与平面所成角的最大值是
D.的最小值为
三、填空题
12.已知复数z的模为2,则的最大值为________.
13.某科研攻关项目中遇到一个问题,请了甲、乙两位专家单独解决此问题,若甲、乙能解决此问题的概率分别为m,n,则此问题被解决的概率为________.
14.滕王阁,江南三大名楼之一,因初唐诗人王勃所作《滕王阁序》中的“落霞与孤鹜齐飞,秋水共长天一色”而名传千古,流芳后世.如图,在滕王阁旁地面上共线的三点A,B,C处测得阁顶端点P的仰角分别为,,.且米,则滕王阁高度________米.
四、解答题
15.已知,,与的夹角是.
(1)求的值及的值;
(2)当k为何值时,?
16.本学期初,某校对全校高一学生进行数学测试(满分100),并从中随机抽取了100名学生的成绩,以此为样本,分,,,,五组,得到如图所示频率分布直方图.
(1)求a的值,并估计该校高一学生数学成绩的平均数和分位数;
(2)为进一步了解学困生的学习情况,从上述数学成绩低于70分的学生中,分层抽样抽出6人,再从6人中任取2人,求此2人分数都在的概率.
17.(1)叙述并证明平面与平面平行的性质定理;
(2)设,是两个不同的平面,m,n是平面,之外的两条不同直线,给出四个论断:①;②;③;④.以其中三个论断作为条件,余下一个作为结论,写出一个正确的命题,并证明.
18.已知向量,,函数.
(1)若,,求的值;
(2)若,,,,求的值;
(3)设中,内角A,B,C所对的边分别为a,b,c,已知,且锐角B满足,求的取值范围.
19.如图,在六面体中,,正方形的边长为2,,,.
(1)证明:平面平面;
(2)求直线EF与平面所成角的正切值;
(3)求平面与平面所成二面角的余弦值;
(4)求多面体的体积.
参考答案
1.答案:D
解析:设7个打分中除了一个最高分10分和一个最低分9分之外的数据为,,,,,
因为,
故可得,
则去掉一个最高分10分和一个最低分9分之后的平均分为;
因为去掉一个最高分和最低分后,数据更加集中,故方差变小.
故选:D.
2.答案:A
解析:.
故选:A
3.答案:A
解析:已知向量,,,
所以,解得.
故选:A.
4.答案:B
解析:对于选项A,如图1,当,满足,,,,时,l与可以斜交,故选项A错误,
对于选项B,因为,,所以,因为,则由线面垂直的判定定理得,故选项B正确,
对于选项C,因为,,所以,因为,所以,故选项C错误,
对于选项D,若,,,则l与m可以相交、平行或异面,如图2,满足,,,而l与m异面,故选项D错误,
故选:B.
5.答案:B
解析:设三人为A,B,C,则参加晚会的情况有A,B,C,AB,AC,BC,ABC,共7种情况,其中恰有一人参加晚会的情况有3种,故所求的概率为.
6.答案:B
解析:设正方体的棱长为a,则其内切球的直径为a,
由题意,解得,即正方体的棱长为4,半径为1的两个球的直径和为4,
故正方体内最多可以放8个半径为1的球.
故选:B
7.答案:B
解析:展开得,
两边同时平方有,
即,解得,
故选:B.
8.答案:C
解析:如图所示,延长交于E,
由已知O为的重心,则点E为的中点,可得,且,
又由,可得D是的四等分点,
则,
因为,所以,,所以.
故选:C.
9.答案:BC
解析:第一种情况:现从角落A沿角的方向把球打出去,球先接触边,反射情况如下:
,,由反射的性质,得,关于对称,,关于对称,
即G,E为的三等分点,因此,C正确;
第二种情况:现从角落A沿角的方向把球打出去,球先接触边,反射情况如下:
,,由反射的性质,得,关于对称,,关于对称,
即G,F为的三等分点,因此,B正确.
故选:BC
10.答案:BD
解析:两次取出的球的数字之和为8,有,,,,,共5种情况,
所以;两次取出的球的数字之和为7,有,,,,,,共6种情况,
所以;;
对于A,,故甲与丙不相互独立,错误;
对于B,,故甲与丁相互独立,正确;
对于C,,故丙与丁不相互独立,错误.
对于D,,故乙与丙不相互独立,正确;
故选:BD.
11.答案:ACD
解析:对于选项A,由正方体性质,易得,,
因为,平面,
所以平面.
因为平面,所以,故A正确;
对于选项B,当P与B重合,则此时与夹角为,故B错误;
对于选项C,如图连接交于H,
因为平面,平面,所以.
因为,,平面,
所以平面,即平面,
所以为直线与平面所成角,所以.
所以当最小时最大,即时,最小.
由,可得,
此时,故的最大值为,
直线与平面所成角的最大值是,故C正确;
对于选项D,如图,将平面与平面沿翻折到同一个平面内
由题意,,,,,,
从而,,故为平行四边形.
又,故为矩形.
从而当P为与交点时,最小,此时,故D正确.
故选:ACD.
12.答案:3
解析:复数z的模为2,表示复数z在复平面内对应的点Z到原点O的距离为2,
则点Z的轨迹是以原点O为圆心,2为半径的圆,
而是圆O上的点到点的距离,
所以.
故答案为:3
13.答案:
解析:记事件“甲专家独立解决”,事件“乙专家独立解决”,
则,,而A,B相互独立,即,
所以,即问题被解决的概率为.
故答案为:
14.答案:
解析:设,因为,,,
所以,,,.
在中,,
即①.,
在中,,
即②,
因为,
所以①②两式相加可得:,解得:,
则,
故答案为:.
15.答案:(1),;
(2).
解析:(1),,与的夹角是,
,
;
(2)由题意,,
即,
解得,
即时,.
16.答案:(1),平均数75.5,分位数88
(2)
解析:(1)由,
解得;
该校高一学生数学成绩的平均数为.
前3组的频率和为,
所以分位数为;
(2)分层抽样抽取的6人中,的有人,记为1,2,
的有人,记为3,4,5,6,
从6人中任取2人,基本事件有12,13,14,15,16,23,24,25,26,34,35,36,45,46,56,共15种,
其中2人分数都在的有34,35,36,45,46,56共6种,
所以从6人中任取2人,分数都在的概率为.
17.答案:(1)答案见解析;
(2)答案见解析
解析:(1)两个平面平行的性质定理:两个平面平行,如果另一个平面与这两个平面相交,那么两条交线平行.
已知:如图,已知,,,求证:.
证明:因为,所以与没有公共点,
又,,所以,,
所以a与b没有公共点,
又,,
;
(2)命题一:若,,,则(②③④①).
证明:过平面和平面外一点P,作,交于A,作,交于B,
则,,,
显然与不平行,设,则、,所以,,
因为,平面,所以平面,
延展平面交l于点M,连接,,平面,
所以,,
则是二面角的一个平面角,
因为,,所以,同理有,
又,所以四边形为矩形,则,
则平面和平面形成的二面角的平面角直二面角,故,
命题二:若,,,则(①③④②).
证明:因为,,,
设,在平面内作直线,根据面面垂直的性质定理可得,
又因为,所以,
因为,,所以,所以.
18.答案:(1);
(2);
(3)
解析:(1)依题意,,
由,得,由,得,则,
则.
(2)由,得,由,得,
则,
由,,得,
则
由,得,
所以的值为.
(3)由,得,而,即,解得,即,则,设,,,,
由正弦定理得,则,,
于是,
所以的取值范围是.
19.答案:(1)证明见解析;
(2);
(3);
(4).
解析:(1)由,平面,平面,得平面,
由正方形,得,又平面,平面,得平面,而,平面,
所以平面平面.
(2)连接,在正方形中,,则,而,,,
即有,,于是,,
而,平面,则平面,由,
得平面,因此在平面内的射影是,
令直线与平面所成的角为,在直角梯形中,,
所以直线EF与平面所成角的正切值为.
(3)延长与的延长线交于点G,连接,则平面平面,
由(2)知,平面,平面,则,
由,,得,取的中点O,连接,,
由,得,而,平面,
则平面,又平面,则,
因此是二面角的平面角,在中,,
而,,则,,
所以平面与平面所成二面角的余弦值是.
(4)由(2)知,平面,而平面,则,又,,平面,于是平面,
四棱锥的体积,
由平面,得三棱锥的体积,
所以多面体的体积.
同课章节目录
