2023~2024学年湖南邵阳邵东市邵东县创新国际实验学校高一上学期期中数学试卷(PDF版含解析)
文档属性
| 名称 | 2023~2024学年湖南邵阳邵东市邵东县创新国际实验学校高一上学期期中数学试卷(PDF版含解析) |  | |
| 格式 | |||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 22:20:18 | ||
图片预览




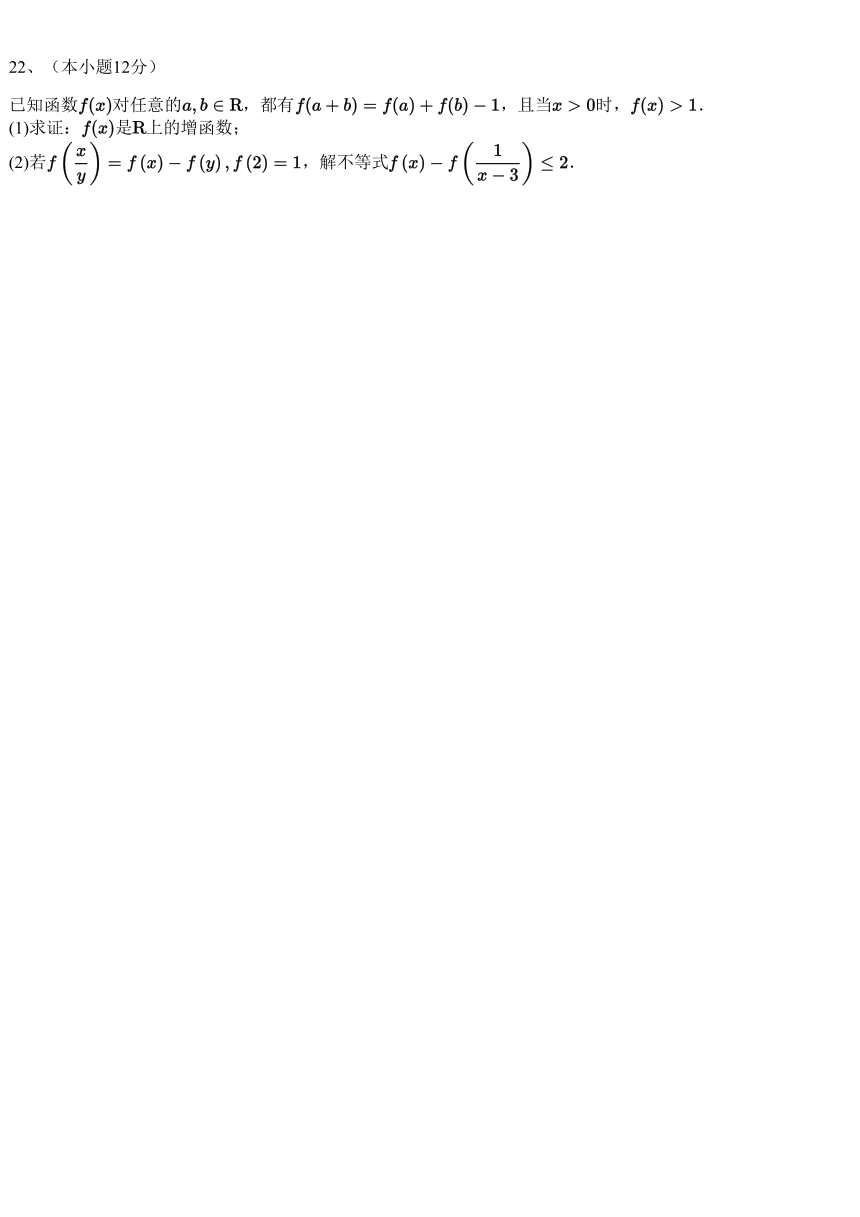
文档简介
2023~2024学年湖南邵阳邵东市邵东县创新国际实验学校高一上学期期中
数学试卷
一、单选题(本大题共8小题,每小题5分,共40分)
1、已知集合 , ,则 ( )
A.
B.
C.
D.
2、函数 的定义域是( )
A.
B.
C.
D.
3、已知全集 ,集合 或 , ,那么阴影部分表示的集合为
A.
B. 或
C.
D.
4、关于 的不等式 的解集为空集,则 的取值范围为( )
A.
B.
C.
D.
5、若函数 在R上是单调函数,则 的取值可以是( )
A.0
B.1
C.2
D.3
6、已知正数a,b满足 ,则 的最小值为( )
A.
B.
C.
D.
7、设 R,则“ >1”是“ >1”的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
8、定义在R上的函数 ,对任意的 1 2 ( 1 2),都有 ,且 3 2,则不等
式 1 2的解集为( )
A. 2
B. 2
C. 4
D. 4
二、多选题(本大题共4小题,每小题5分,共20分)
9、在下列四组函数中, 与 不表示同一函数的是( )
A.
B. ,
C.
D.
10、若 ,则下列命题正确的是( )
A.若 ,则
B.若 ,则
C.若 , ,则
D.若 ,则
11、如图所示是函数 的图象,图中 正半轴曲线与虚线无限接近但是永不相交,则以下描述正确的是
( )
A.函数 的定义域为
B.函数 的值域为 ,+
C.此函数在定义域内是增函数
D.对于任意的 ,都有唯一的自变量 与之对应
12、已知函数 为R上的奇函数, 为偶函数,则( )
A.
B.
C.
D.
三、填空题(本大题共4小题,每小题5分,共20分)
13、不等式 的解集是 .
14、命题“ , ”的否定是 .
15、幂函数 为偶函数,且在 上是减函数,则 .
16、已知 ,则
四、解答题(本大题共6小题,共70分)
17、(本小题10分)
已知集合 , .
(1)若 ,求 ;
(2)若 ,求 实数a的取值范围.
18、(本小题12分)
已知函数 ,
(1)判断函数 在 , 上的单调性,并用定义证明;
2 ( )若 ,求实数 的取值范围.
19、(本小题12分)
已知函数 , .
(1)若 , ,求 , 的最小值;
(2)若 恒成立,求证: .
20、(本小题12分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新
建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造
价为180元/m,设利用的旧墙的长度为x(单位:元).设修建此矩形场地围墙的总费用为y.
(Ⅰ)将y表示为x的函数;
(Ⅱ)试确定x,使修建此矩 形场地围墙的总费用最小,并求出最小总费用.
21、(本小题12分)
已知函数 是定义在 上的奇函数,且 .
(1)求函数 的解析式;
(2)判断并证明 在 上的单调性,并求若存在实数 ,使得不等式 有
解,求实数m的取值范围.
22、(本小题12分)
已知函数 对任意的 ,都有 ,且当 时, .
(1)求证: 是 上的增函数;
(2)若 ,解不等式 .
参考答案
一、单选题
1、
<答 案>:
B
<解析>:
, ,
,
故选:B.
2、
<答 案>:
D
<解析>:
函数 ,
> < <
则 ,即 ,即 定义域是 .
故选:D
3、
<答 案>:
D
<解析>:
阴影部分表示的集合为 ,
或
因此正确答案为
4、
<答 案>:
C
<解析>:
当 时,不等式化为 ,解集为空集,符合题意.
当 时,不等式 的解集不是空集 ,不符合题意.
当 时,要使不等式 的解集为空集,
则需 ,解得 .
综上所述, 的取值范围是 .
故选:C
5、
<答 案>:
B
<解析>:
因为当 时,函数 为单调递增函数,
又函数 在R上是单调函数,则需满足 ,解得 ,
所以实数 的范围为 ,
所以满足范围的选项是选项B.
故选:B.
6、
<答 案>:
C
<解析>:
解:因为 ,
所以 ,
所以 ,
当且仅当 ,即 , 时,等号成立.
故选:C
7、
<答 案>:
A
<解析>:
试题分析:由 可得 成立,反之不成立,所以“ ”是“ ”的充分不必要条件
考点:充分条件与必要条件
8、
<答 案>:
C
<解析>:
因为对任意的 1 2 ( 1 2),都有 ,所以 在R上单调递增.因为 3 2,
所以 2的解集为 3 ,则 1 2的解集为 4 .
故选:C
二、多选题
9、
<答 案>:
A;C;D
<解析>:
对于A, 的定义域为 ,而 的定义域为 ,所以不是同一函数;
对于B,因为 时, ; 时, ;所以 表示同一函数;
对于C, 的定义域为 ,而 的定义域为 ,所以不是同一函数;
对于D, 的定义域为 ,而 的定义域为 ,所以不是同一函数;
故选:ACD.
10、
<答案 >:
A;C;D
<解析>:
对于A中,若 ,则 ,所以 ,所以A正确;
对于B中,若 ,当 时, ;当 时, ;当 时, ,所以B不正确;
对于C中,若 , ,根据不等式的基本性质,可得 ,所以C正确;
对于D中,若 ,可得 ,所以 ,所以D正确.
故选:ACD.
11、
<答案 >:
B;D
<解析>:
由图象知:
A.函数 的 定义域为 ,故错误;
B.函数 的值域为 ,+ ,故正确;
C. 函数 在 , 上递增,但 在定义域内不单调,故错误;
D.对于任意的 ,都有唯一的自变量 与之对应,故正确;
故选:BD
12、
<答案 >:
B;C
<解析>:
因为 为R上的奇函数,所以 ;
因为 为偶函数,所以 ,故B正确;
由 可得 ,所以 ;
因为 ,其结果不一定为零,故A不正确 ;
由 得 ,所以 ,故C正确 ;
由 得 ,所以周期为4,
所以 ,因为 从题目 无法得出,故D不正确;
故选:BC.
三、填空题
13、
<答案 >:
或
<解析>:
解:由 ,可得 ,
即 ,
令 ,
解得 ,
所以不等式 的解集为 或 ,
即不等 的解集为 或 .
故答案为: 或 .
14、
<答案 >:
,
<解析>:
命题“ , ”是全称量词命题,
其否定是: , .
故答案为: ,
15、
<答案 >:
3
<解析>:
由幂函数 为偶函数,且在(0,+∞)上是单调递减函数,可得m2-2m-3<
0,且m2-2m-3为偶数,m∈Z,且 = .解出即可.
∵ 幂函数 为偶函数,且在 上是减函数,
∴ ,且 为偶数, ,且 = .
解得 , ,1,2,
且 =2,
只有 时满足 = 为偶数.
∴ .
故答案为: 3.
16、
<答案 >:
/
<解析>:
解:因为 ,所以 ,
所以 ,
所以
故答案为:
四、解答题
17、
<答案 >:
(1)
(2)
<解析>:
(1)若 ,则 ,
因为 ,所以 ;
2 ( )由题,得 或 ,由 ,得 ,
若 ,则 ,得 ,
若 ,即 时,则有 , 或 ,得 或 ,
综上,
18、
<答案 >:
(1)函数f(x)在 , 上为减函数,证明见解析;(2) .
<解析>:
解:(1)任取 , ,且 ,
则
,
,
即 ,
所以函数f(x)在 , 上为减函数;
(2)由(1)得 ,
所以实数 的取值范围 .
19、
<答案 >:
(1)
(2)证明见解析
<解析>:
(1)解:若 , ,则 ,
当且仅当 ,即当 时,取等号,所以 .
(2)证明:因为 恒成立,即 恒成立,
所以 ,所以, ,即 .
20、
<答案 >:
(Ⅰ)y=225x+
(Ⅱ)当x=24m时,修建围墙的总费用最小,最小总费用是10440元.
<解析>:
试题分析:(1)设矩形的另一边长为am,则根据围建的矩形场地的面积为360m2,易得 ,此时再根据
旧墙的维修费用为45元/m,新墙的造价为180元/m,我们即可得到修建围墙的总费用y表示成x的函数的解析
式;(2)根据(1)中所得函数的解析式,利用基本不等式,我们易求出修建此矩形场地围墙的总费用最小
值,及相应的x值
试题解析:(1) 如图,设矩形的另一边长为a m
则 45x+180(x-2)+180·2a=225x+360a-360
由已知xa=360,得a= ,
所以y=225x+
(2)
.当且仅当225x= 时,等号成立.
即当x=24m时,修建围墙的总费用最小,最小总费用是10440元.
考点:函数模型的选择与应用
21、
<答案 >:
(1)
(2) 在 上单调递增,
<解析>:
(1)∵ 为定义在 上的奇函数,∴ ,则有 ,
由 得 ,∴ , ,
又 ,∴ , , .
(2) 在 上单调递增,证明如下:
任取 , ,
∵ ,∴ , ,且 , ,
∴ ,∴ , 在 上单调递增;
由上可知 在 上单调递增,∴ , .
令 ,则有 ,
令 , ,
,∴ .
22、
<答案 >:
(1)证明见解析
(2)
<解析>:
(1)设 ,且 ,
则 ,即 ,
所以 ,
所以 ,所以 是 上的增函数.
(2)因为 ,所以 .
在上式中取 ,则有 ,
因为 ,所以 .
于是不等式 等价于 .
又由(1)知 是 上的增函数,
所以 ,解得 或 ,
所以原不等式的解集为 .
数学试卷
一、单选题(本大题共8小题,每小题5分,共40分)
1、已知集合 , ,则 ( )
A.
B.
C.
D.
2、函数 的定义域是( )
A.
B.
C.
D.
3、已知全集 ,集合 或 , ,那么阴影部分表示的集合为
A.
B. 或
C.
D.
4、关于 的不等式 的解集为空集,则 的取值范围为( )
A.
B.
C.
D.
5、若函数 在R上是单调函数,则 的取值可以是( )
A.0
B.1
C.2
D.3
6、已知正数a,b满足 ,则 的最小值为( )
A.
B.
C.
D.
7、设 R,则“ >1”是“ >1”的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
8、定义在R上的函数 ,对任意的 1 2 ( 1 2),都有 ,且 3 2,则不等
式 1 2的解集为( )
A. 2
B. 2
C. 4
D. 4
二、多选题(本大题共4小题,每小题5分,共20分)
9、在下列四组函数中, 与 不表示同一函数的是( )
A.
B. ,
C.
D.
10、若 ,则下列命题正确的是( )
A.若 ,则
B.若 ,则
C.若 , ,则
D.若 ,则
11、如图所示是函数 的图象,图中 正半轴曲线与虚线无限接近但是永不相交,则以下描述正确的是
( )
A.函数 的定义域为
B.函数 的值域为 ,+
C.此函数在定义域内是增函数
D.对于任意的 ,都有唯一的自变量 与之对应
12、已知函数 为R上的奇函数, 为偶函数,则( )
A.
B.
C.
D.
三、填空题(本大题共4小题,每小题5分,共20分)
13、不等式 的解集是 .
14、命题“ , ”的否定是 .
15、幂函数 为偶函数,且在 上是减函数,则 .
16、已知 ,则
四、解答题(本大题共6小题,共70分)
17、(本小题10分)
已知集合 , .
(1)若 ,求 ;
(2)若 ,求 实数a的取值范围.
18、(本小题12分)
已知函数 ,
(1)判断函数 在 , 上的单调性,并用定义证明;
2 ( )若 ,求实数 的取值范围.
19、(本小题12分)
已知函数 , .
(1)若 , ,求 , 的最小值;
(2)若 恒成立,求证: .
20、(本小题12分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新
建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造
价为180元/m,设利用的旧墙的长度为x(单位:元).设修建此矩形场地围墙的总费用为y.
(Ⅰ)将y表示为x的函数;
(Ⅱ)试确定x,使修建此矩 形场地围墙的总费用最小,并求出最小总费用.
21、(本小题12分)
已知函数 是定义在 上的奇函数,且 .
(1)求函数 的解析式;
(2)判断并证明 在 上的单调性,并求若存在实数 ,使得不等式 有
解,求实数m的取值范围.
22、(本小题12分)
已知函数 对任意的 ,都有 ,且当 时, .
(1)求证: 是 上的增函数;
(2)若 ,解不等式 .
参考答案
一、单选题
1、
<答 案>:
B
<解析>:
, ,
,
故选:B.
2、
<答 案>:
D
<解析>:
函数 ,
> < <
则 ,即 ,即 定义域是 .
故选:D
3、
<答 案>:
D
<解析>:
阴影部分表示的集合为 ,
或
因此正确答案为
4、
<答 案>:
C
<解析>:
当 时,不等式化为 ,解集为空集,符合题意.
当 时,不等式 的解集不是空集 ,不符合题意.
当 时,要使不等式 的解集为空集,
则需 ,解得 .
综上所述, 的取值范围是 .
故选:C
5、
<答 案>:
B
<解析>:
因为当 时,函数 为单调递增函数,
又函数 在R上是单调函数,则需满足 ,解得 ,
所以实数 的范围为 ,
所以满足范围的选项是选项B.
故选:B.
6、
<答 案>:
C
<解析>:
解:因为 ,
所以 ,
所以 ,
当且仅当 ,即 , 时,等号成立.
故选:C
7、
<答 案>:
A
<解析>:
试题分析:由 可得 成立,反之不成立,所以“ ”是“ ”的充分不必要条件
考点:充分条件与必要条件
8、
<答 案>:
C
<解析>:
因为对任意的 1 2 ( 1 2),都有 ,所以 在R上单调递增.因为 3 2,
所以 2的解集为 3 ,则 1 2的解集为 4 .
故选:C
二、多选题
9、
<答 案>:
A;C;D
<解析>:
对于A, 的定义域为 ,而 的定义域为 ,所以不是同一函数;
对于B,因为 时, ; 时, ;所以 表示同一函数;
对于C, 的定义域为 ,而 的定义域为 ,所以不是同一函数;
对于D, 的定义域为 ,而 的定义域为 ,所以不是同一函数;
故选:ACD.
10、
<答案 >:
A;C;D
<解析>:
对于A中,若 ,则 ,所以 ,所以A正确;
对于B中,若 ,当 时, ;当 时, ;当 时, ,所以B不正确;
对于C中,若 , ,根据不等式的基本性质,可得 ,所以C正确;
对于D中,若 ,可得 ,所以 ,所以D正确.
故选:ACD.
11、
<答案 >:
B;D
<解析>:
由图象知:
A.函数 的 定义域为 ,故错误;
B.函数 的值域为 ,+ ,故正确;
C. 函数 在 , 上递增,但 在定义域内不单调,故错误;
D.对于任意的 ,都有唯一的自变量 与之对应,故正确;
故选:BD
12、
<答案 >:
B;C
<解析>:
因为 为R上的奇函数,所以 ;
因为 为偶函数,所以 ,故B正确;
由 可得 ,所以 ;
因为 ,其结果不一定为零,故A不正确 ;
由 得 ,所以 ,故C正确 ;
由 得 ,所以周期为4,
所以 ,因为 从题目 无法得出,故D不正确;
故选:BC.
三、填空题
13、
<答案 >:
或
<解析>:
解:由 ,可得 ,
即 ,
令 ,
解得 ,
所以不等式 的解集为 或 ,
即不等 的解集为 或 .
故答案为: 或 .
14、
<答案 >:
,
<解析>:
命题“ , ”是全称量词命题,
其否定是: , .
故答案为: ,
15、
<答案 >:
3
<解析>:
由幂函数 为偶函数,且在(0,+∞)上是单调递减函数,可得m2-2m-3<
0,且m2-2m-3为偶数,m∈Z,且 = .解出即可.
∵ 幂函数 为偶函数,且在 上是减函数,
∴ ,且 为偶数, ,且 = .
解得 , ,1,2,
且 =2,
只有 时满足 = 为偶数.
∴ .
故答案为: 3.
16、
<答案 >:
/
<解析>:
解:因为 ,所以 ,
所以 ,
所以
故答案为:
四、解答题
17、
<答案 >:
(1)
(2)
<解析>:
(1)若 ,则 ,
因为 ,所以 ;
2 ( )由题,得 或 ,由 ,得 ,
若 ,则 ,得 ,
若 ,即 时,则有 , 或 ,得 或 ,
综上,
18、
<答案 >:
(1)函数f(x)在 , 上为减函数,证明见解析;(2) .
<解析>:
解:(1)任取 , ,且 ,
则
,
,
即 ,
所以函数f(x)在 , 上为减函数;
(2)由(1)得 ,
所以实数 的取值范围 .
19、
<答案 >:
(1)
(2)证明见解析
<解析>:
(1)解:若 , ,则 ,
当且仅当 ,即当 时,取等号,所以 .
(2)证明:因为 恒成立,即 恒成立,
所以 ,所以, ,即 .
20、
<答案 >:
(Ⅰ)y=225x+
(Ⅱ)当x=24m时,修建围墙的总费用最小,最小总费用是10440元.
<解析>:
试题分析:(1)设矩形的另一边长为am,则根据围建的矩形场地的面积为360m2,易得 ,此时再根据
旧墙的维修费用为45元/m,新墙的造价为180元/m,我们即可得到修建围墙的总费用y表示成x的函数的解析
式;(2)根据(1)中所得函数的解析式,利用基本不等式,我们易求出修建此矩形场地围墙的总费用最小
值,及相应的x值
试题解析:(1) 如图,设矩形的另一边长为a m
则 45x+180(x-2)+180·2a=225x+360a-360
由已知xa=360,得a= ,
所以y=225x+
(2)
.当且仅当225x= 时,等号成立.
即当x=24m时,修建围墙的总费用最小,最小总费用是10440元.
考点:函数模型的选择与应用
21、
<答案 >:
(1)
(2) 在 上单调递增,
<解析>:
(1)∵ 为定义在 上的奇函数,∴ ,则有 ,
由 得 ,∴ , ,
又 ,∴ , , .
(2) 在 上单调递增,证明如下:
任取 , ,
∵ ,∴ , ,且 , ,
∴ ,∴ , 在 上单调递增;
由上可知 在 上单调递增,∴ , .
令 ,则有 ,
令 , ,
,∴ .
22、
<答案 >:
(1)证明见解析
(2)
<解析>:
(1)设 ,且 ,
则 ,即 ,
所以 ,
所以 ,所以 是 上的增函数.
(2)因为 ,所以 .
在上式中取 ,则有 ,
因为 ,所以 .
于是不等式 等价于 .
又由(1)知 是 上的增函数,
所以 ,解得 或 ,
所以原不等式的解集为 .
同课章节目录
