北师大版数学九年级上册 专项练习十 多边形相似与三角形相似(含答案)
文档属性
| 名称 | 北师大版数学九年级上册 专项练习十 多边形相似与三角形相似(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 450.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-01 12:10:34 | ||
图片预览

文档简介
专项练习十 多边形相似与三角形相似
时间:30分钟 满分:60分
一、选择题(每小题3分,共15分)
1.用一个放大镜看一个四边形 ABCD,若四边形的边长被放大为原来的10倍,则下列结论正确的是( )
A.放大后的∠B 是原来∠B 的10倍
B.两个四边形的对应边相等
C.两个四边形的对应角相等
D.以上答案都不正确
2.如图,在大小为4×4 的正方形网格中,是相似三角形的是( )
A.①和② B.②和③
C.①和③ D.②和④
3.如图,直角梯形 ABCD 中,AB∥CD,∠C=90°,∠BDA=90°,AB=a,BD=b,CD=c,BC=d,AD=e,则下列等式成立的是( )
C. be=ac
D. bd=ae
4.如图,下列条件:
①∠1=∠2;②∠ADB=∠ABC;③AB=AD· 能使△ABD∽△ACB 的个数为( )
A.1 B.2
C.3 D.4
5.如图,在□ABCD 中,E 为AD 的三等分点, 连接 BE,交 AC 于点 F,AC=12,则AF为( )
A.4 B.4.8
C.5.2 D.6
二、填空题(每小题4分,共16分)
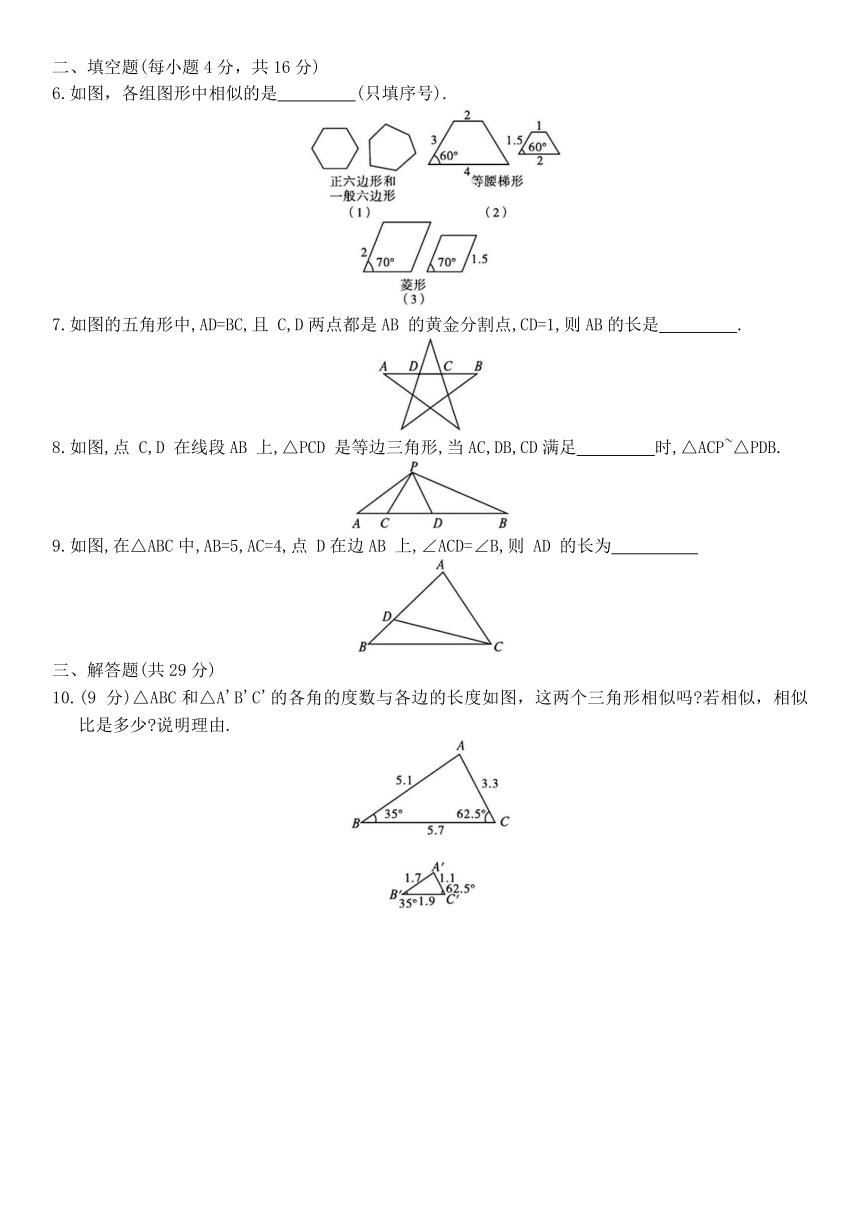
6.如图,各组图形中相似的是 (只填序号).
7.如图的五角形中,AD=BC,且 C,D两点都是AB 的黄金分割点,CD=1,则AB的长是 .
8.如图,点 C,D 在线段AB 上,△PCD 是等边三角形,当AC,DB,CD满足 时,△ACP~△PDB.
9.如图,在△ABC中,AB=5,AC=4,点 D在边AB 上,∠ACD=∠B,则 AD 的长为
三、解答题(共29分)
10.(9 分)△ABC和△A'B'C'的各角的度数与各边的长度如图,这两个三角形相似吗 若相似,相似比是多少 说明理由.
11.(10 分)宽与长的比等于黄金分割比的矩形,它在日常生活中有着广泛的应用.我们来研究一下这个矩形,如图,矩形ABCD 是一个黄金分割矩形,设AB=a,则
则AD= (用带根号的式子表示).
(2)在AB 上截取线段AM=AD,在 DC上截取线段 DN = DA, 则 BM = a, 连 接 MN, 则 四边 形MNDA 是 形.
(3)计算 BM: BC的值,你发现了什么 用语言描述你发现的结论.
12.(10分)如图,在等腰△ABC 中, AB =AC,D 为CB 延长线上一点,E 为 BC 延长线上一点,满足 求证:△ADB∽△EAC.
专项练习十 多边形相似与三角形相似
1. C 2. C 3. A 4. C 5. B
6.(2) (3) 7. +2 8. CD =AC·DB
9.
10.解 相似,相似比为3:1,理由如下:
又
∴根据相似图形的定义可知△ABC与△A'B'C'相似,相似比为3:1.
11.解(1) a。 正方
结论:在黄金分割矩形中,截掉一个边长等于宽的正方形,剩下的矩形仍为黄金分割矩形.
12.证明在等腰△ABC中,AB=AC,
∴∠ABC=∠ACB.
又点D,B,C,E在同一条直线上,
∴△ADB∽△EAC.
时间:30分钟 满分:60分
一、选择题(每小题3分,共15分)
1.用一个放大镜看一个四边形 ABCD,若四边形的边长被放大为原来的10倍,则下列结论正确的是( )
A.放大后的∠B 是原来∠B 的10倍
B.两个四边形的对应边相等
C.两个四边形的对应角相等
D.以上答案都不正确
2.如图,在大小为4×4 的正方形网格中,是相似三角形的是( )
A.①和② B.②和③
C.①和③ D.②和④
3.如图,直角梯形 ABCD 中,AB∥CD,∠C=90°,∠BDA=90°,AB=a,BD=b,CD=c,BC=d,AD=e,则下列等式成立的是( )
C. be=ac
D. bd=ae
4.如图,下列条件:
①∠1=∠2;②∠ADB=∠ABC;③AB=AD· 能使△ABD∽△ACB 的个数为( )
A.1 B.2
C.3 D.4
5.如图,在□ABCD 中,E 为AD 的三等分点, 连接 BE,交 AC 于点 F,AC=12,则AF为( )
A.4 B.4.8
C.5.2 D.6
二、填空题(每小题4分,共16分)
6.如图,各组图形中相似的是 (只填序号).
7.如图的五角形中,AD=BC,且 C,D两点都是AB 的黄金分割点,CD=1,则AB的长是 .
8.如图,点 C,D 在线段AB 上,△PCD 是等边三角形,当AC,DB,CD满足 时,△ACP~△PDB.
9.如图,在△ABC中,AB=5,AC=4,点 D在边AB 上,∠ACD=∠B,则 AD 的长为
三、解答题(共29分)
10.(9 分)△ABC和△A'B'C'的各角的度数与各边的长度如图,这两个三角形相似吗 若相似,相似比是多少 说明理由.
11.(10 分)宽与长的比等于黄金分割比的矩形,它在日常生活中有着广泛的应用.我们来研究一下这个矩形,如图,矩形ABCD 是一个黄金分割矩形,设AB=a,则
则AD= (用带根号的式子表示).
(2)在AB 上截取线段AM=AD,在 DC上截取线段 DN = DA, 则 BM = a, 连 接 MN, 则 四边 形MNDA 是 形.
(3)计算 BM: BC的值,你发现了什么 用语言描述你发现的结论.
12.(10分)如图,在等腰△ABC 中, AB =AC,D 为CB 延长线上一点,E 为 BC 延长线上一点,满足 求证:△ADB∽△EAC.
专项练习十 多边形相似与三角形相似
1. C 2. C 3. A 4. C 5. B
6.(2) (3) 7. +2 8. CD =AC·DB
9.
10.解 相似,相似比为3:1,理由如下:
又
∴根据相似图形的定义可知△ABC与△A'B'C'相似,相似比为3:1.
11.解(1) a。 正方
结论:在黄金分割矩形中,截掉一个边长等于宽的正方形,剩下的矩形仍为黄金分割矩形.
12.证明在等腰△ABC中,AB=AC,
∴∠ABC=∠ACB.
又点D,B,C,E在同一条直线上,
∴△ADB∽△EAC.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
