北师大版数学九年级上册 专项练习十一 相似与位似(含答案)
文档属性
| 名称 | 北师大版数学九年级上册 专项练习十一 相似与位似(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 708.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-01 00:00:00 | ||
图片预览

文档简介
专项练习十一 相似与位似
时间:30分钟 满分:60分
一、选择题(每小题3分,共18分)
1.有两个三角形相似,它们的对应中线的比为5:7,那么下列结论错误的是( )
A.这两个相似三角形对应边的比为5:7
B.这两个相似三角形对应高的比为5:7
C.这两个相似三角形对应角平分线的比为5:7
D.这两个相似三角形的相似比为7:5
2.将一个三角形改成与它相似的三角形,如果面积扩大为原来的9倍,那么周长扩大为原来的( )
A.9倍 B.3倍
C.81倍 D.18倍
3.如图,按如下方法将△ABC 的三边缩小到原来的 ,任取一点 O,连接OA,OB,OC,并取它们的中点 D、E、F,得△EDF,则下列说法正确的有( )
① △ABC 与 △DEF 是 位 似 图 形
②△ABC 与 △DEF 是 相 似 图 形
③△ABC与△DEF 的周长比为 2 : 1
④△ABC与△DEF的面积比为4:1
A.1个 B.2个 C.3个 D.4个
4.如图是△ABC的位似图形的几种画法,其中正确的有( )
A.1个 B.2个
C.3个 D.4个
5.如图,在直角坐标 系 中,矩 形OABC 的 顶 点O在坐标原点,边 OA 在 x 轴上,边 OC 在 y轴上,如果矩形OA'B'C'与矩形OABC 关于点O 位似,且矩形OA'B'C'的面积等于矩形OABC 面积的 ,那么点 B'的坐标是( )
A.(-2,3)
B.(2,-3)
C.(3,-2)或(-2,3)
D.(-2,3)或(2,-3)
6.如图,点O是等边三角形 PQR 的中心,P',Q',R'分别是OP,OQ, OR 的中 点, 则△P'Q'R'与△PQR 是位似三角形.此时,△P'Q'R'与△PQR 的相似比、位似中心分别为( )
A.2、点 P B. 、点P
C.2、点O D. 、点O
二、填空题(每小题4分,共16分)
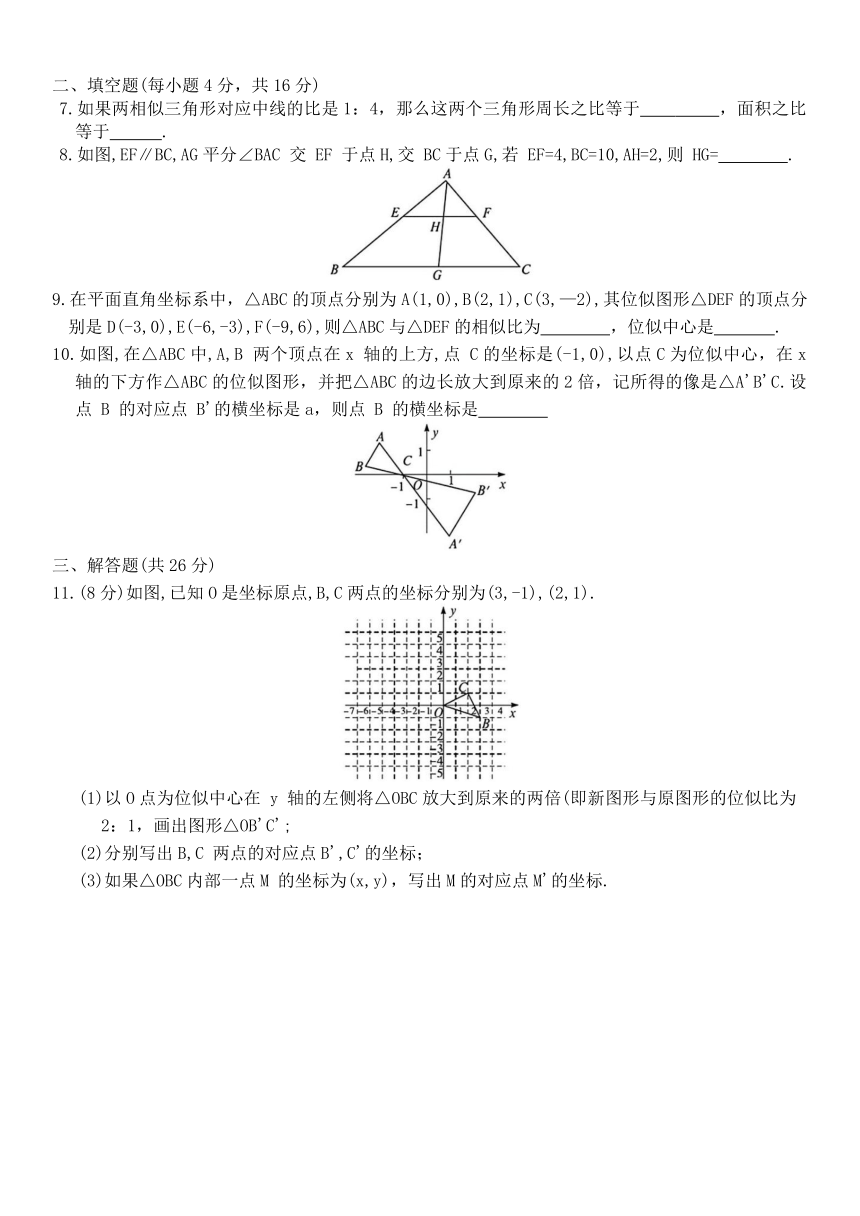
7.如果两相似三角形对应中线的比是1:4,那么这两个三角形周长之比等于 ,面积之比等于 .
8.如图,EF∥BC,AG平分∠BAC 交 EF 于点H,交 BC于点G,若 EF=4,BC=10,AH=2,则 HG= .
9.在平面直角坐标系中,△ABC的顶点分别为A(1,0),B(2,1),C(3,—2),其位似图形△DEF的顶点分别是D(-3,0),E(-6,-3),F(-9,6),则△ABC与△DEF的相似比为 ,位似中心是 .
10.如图,在△ABC中,A,B 两个顶点在x 轴的上方,点 C的坐标是(-1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,记所得的像是△A'B'C.设点 B 的对应点 B'的横坐标是a,则点 B 的横坐标是
三、解答题(共26分)
11.(8分)如图,已知O是坐标原点,B,C两点的坐标分别为(3,-1),(2,1).
(1)以O点为位似中心在 y 轴的左侧将△OBC放大到原来的两倍(即新图形与原图形的位似比为 2:1,画出图形△OB'C';
(2)分别写出B,C 两点的对应点B',C'的坐标;
(3)如果△OBC内部一点M 的坐标为(x,y),写出M的对应点M'的坐标.
12.(9分)已知 ABCD中,如图,E是CD 延长线上的一点,BE与AD 交于点F,DE= CD.
(1)试说明:△ABF∽△CEB;
(2)若△DEF的面积为2,求□ABCD的面积.
13.(9分)如图,马戏团让狮子和公鸡表演跷跷板节目.跷跷板支柱 AB 的高度为1.2米.
(1)若吊环高度为2米,支点 A 为跷跷板PQ的中点,狮子能否将公鸡送到吊环上 为什么
(2)若吊环高度为3.6米,在不改变其他条件的前提下移动支柱,当支点 A移到跷跷板 PQ 的什么位置时,狮子刚好能将公鸡送到吊环上
专项练习十一 相似与位似
1. D 2. B 3. D 4. D 5. D 6. D
7.1: 4 1:16 8.3 9.1: 3 坐标原点
11.解(1)如图,△OB'C'即为所求图形.
(2)B'(-6,2),C'(-4,-2).
(3)由于位似比为2:1,所以M'(-2x,-2y).
12.解(1)因为四边形ABCD是平行四边形,所以∠DAB=∠BCE.
又因为AB∥CD,所以∠ABF=∠CEB,所以△ABF∽△CEB.
(2)因为四边形ABCD是平行四边形,所以AD∥BC,AB∥CD,所以△DEF∽△CEB,△DEF∽△ABF.
因为 所以
因为 所以
所以
所以
13.解(1)如图,当狮子将跷跷板 P 端按到底时可得到 Rt△PHQ,易得△PAB∽△PQH.又A为PQ的中点,所以 所以QH=2AB=2.4>2(米).所以狮子能将公鸡送到吊环上.
(2)由△PAB∽△PQH,AB=1.2,QH=3.6,得 所以支点 A移到跷跷板PQ的三分之一处时,狮子刚好能将公鸡送到吊环上.
时间:30分钟 满分:60分
一、选择题(每小题3分,共18分)
1.有两个三角形相似,它们的对应中线的比为5:7,那么下列结论错误的是( )
A.这两个相似三角形对应边的比为5:7
B.这两个相似三角形对应高的比为5:7
C.这两个相似三角形对应角平分线的比为5:7
D.这两个相似三角形的相似比为7:5
2.将一个三角形改成与它相似的三角形,如果面积扩大为原来的9倍,那么周长扩大为原来的( )
A.9倍 B.3倍
C.81倍 D.18倍
3.如图,按如下方法将△ABC 的三边缩小到原来的 ,任取一点 O,连接OA,OB,OC,并取它们的中点 D、E、F,得△EDF,则下列说法正确的有( )
① △ABC 与 △DEF 是 位 似 图 形
②△ABC 与 △DEF 是 相 似 图 形
③△ABC与△DEF 的周长比为 2 : 1
④△ABC与△DEF的面积比为4:1
A.1个 B.2个 C.3个 D.4个
4.如图是△ABC的位似图形的几种画法,其中正确的有( )
A.1个 B.2个
C.3个 D.4个
5.如图,在直角坐标 系 中,矩 形OABC 的 顶 点O在坐标原点,边 OA 在 x 轴上,边 OC 在 y轴上,如果矩形OA'B'C'与矩形OABC 关于点O 位似,且矩形OA'B'C'的面积等于矩形OABC 面积的 ,那么点 B'的坐标是( )
A.(-2,3)
B.(2,-3)
C.(3,-2)或(-2,3)
D.(-2,3)或(2,-3)
6.如图,点O是等边三角形 PQR 的中心,P',Q',R'分别是OP,OQ, OR 的中 点, 则△P'Q'R'与△PQR 是位似三角形.此时,△P'Q'R'与△PQR 的相似比、位似中心分别为( )
A.2、点 P B. 、点P
C.2、点O D. 、点O
二、填空题(每小题4分,共16分)
7.如果两相似三角形对应中线的比是1:4,那么这两个三角形周长之比等于 ,面积之比等于 .
8.如图,EF∥BC,AG平分∠BAC 交 EF 于点H,交 BC于点G,若 EF=4,BC=10,AH=2,则 HG= .
9.在平面直角坐标系中,△ABC的顶点分别为A(1,0),B(2,1),C(3,—2),其位似图形△DEF的顶点分别是D(-3,0),E(-6,-3),F(-9,6),则△ABC与△DEF的相似比为 ,位似中心是 .
10.如图,在△ABC中,A,B 两个顶点在x 轴的上方,点 C的坐标是(-1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,记所得的像是△A'B'C.设点 B 的对应点 B'的横坐标是a,则点 B 的横坐标是
三、解答题(共26分)
11.(8分)如图,已知O是坐标原点,B,C两点的坐标分别为(3,-1),(2,1).
(1)以O点为位似中心在 y 轴的左侧将△OBC放大到原来的两倍(即新图形与原图形的位似比为 2:1,画出图形△OB'C';
(2)分别写出B,C 两点的对应点B',C'的坐标;
(3)如果△OBC内部一点M 的坐标为(x,y),写出M的对应点M'的坐标.
12.(9分)已知 ABCD中,如图,E是CD 延长线上的一点,BE与AD 交于点F,DE= CD.
(1)试说明:△ABF∽△CEB;
(2)若△DEF的面积为2,求□ABCD的面积.
13.(9分)如图,马戏团让狮子和公鸡表演跷跷板节目.跷跷板支柱 AB 的高度为1.2米.
(1)若吊环高度为2米,支点 A 为跷跷板PQ的中点,狮子能否将公鸡送到吊环上 为什么
(2)若吊环高度为3.6米,在不改变其他条件的前提下移动支柱,当支点 A移到跷跷板 PQ 的什么位置时,狮子刚好能将公鸡送到吊环上
专项练习十一 相似与位似
1. D 2. B 3. D 4. D 5. D 6. D
7.1: 4 1:16 8.3 9.1: 3 坐标原点
11.解(1)如图,△OB'C'即为所求图形.
(2)B'(-6,2),C'(-4,-2).
(3)由于位似比为2:1,所以M'(-2x,-2y).
12.解(1)因为四边形ABCD是平行四边形,所以∠DAB=∠BCE.
又因为AB∥CD,所以∠ABF=∠CEB,所以△ABF∽△CEB.
(2)因为四边形ABCD是平行四边形,所以AD∥BC,AB∥CD,所以△DEF∽△CEB,△DEF∽△ABF.
因为 所以
因为 所以
所以
所以
13.解(1)如图,当狮子将跷跷板 P 端按到底时可得到 Rt△PHQ,易得△PAB∽△PQH.又A为PQ的中点,所以 所以QH=2AB=2.4>2(米).所以狮子能将公鸡送到吊环上.
(2)由△PAB∽△PQH,AB=1.2,QH=3.6,得 所以支点 A移到跷跷板PQ的三分之一处时,狮子刚好能将公鸡送到吊环上.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
