2.1 等式性质与不等式性质(共2课时) 课件(共30张PPT)-2024-2025学年高一上学期数学人教A版(2019)必修第一册
文档属性
| 名称 | 2.1 等式性质与不等式性质(共2课时) 课件(共30张PPT)-2024-2025学年高一上学期数学人教A版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-01 15:05:02 | ||
图片预览








文档简介
(共30张PPT)
2.1 等式性质与不等式性质
1 比较两数(式)的大小
目录
2 重要不等式
3 不等式的性质
4 题型
00
引入课题
高与矮
在现实世界和日常生活中,大量存在着相等关系和不等关系,例如多与少、大与小、重与轻、长与短、高与矮、远与近、升与降、涨与跌、不超过和不少于等。类似于这样的问题反映在数量关系上就是相等和不相等,相等用等式表示,不等用不等式表示。
目录
1 比较两数(式)的大小
01
新知探究
问题2你能用不等式或不等式组表示下列问题中的不等关系吗?
01
新知探究
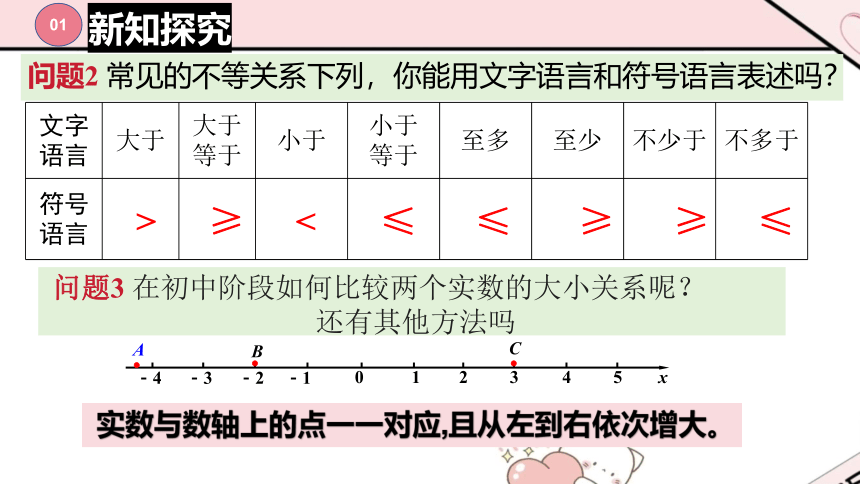
问题2 常见的不等关系下列,你能用文字语言和符号语言表述吗?
文字 语言 大于 大于 等于 小于 小于 等于 至多 至少 不少于 不多于
符号 语言
>
≥
<
≤
≤
≤
≥
≥
问题3 在初中阶段如何比较两个实数的大小关系呢?
还有其他方法吗
x
0
1
2
3
-1
-2
4
5
-3
-4
C
B
A
实数与数轴上的点一一对应,且从左到右依次增大。
01
新知1——比较两数(式)的大小
A
B
b
x
(B)
A
(b)
x
B
A
b
x
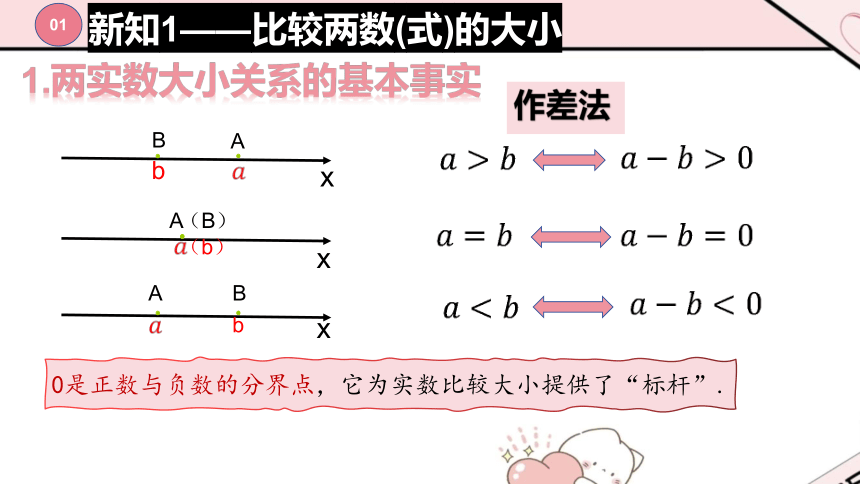
1.两实数大小关系的基本事实
0是正数与负数的分界点,它为实数比较大小提供了“标杆”.
作差法
练一练
练一练
例 2.已知a≥1,试比较
和 的大小.
作商法
练一练
例 3. 比较(x-3)2与(x-2)(x-4)的大小.
解:
(x-3)2-(x-2)(x-4)=x2-6x+9-x2+6x-8=1>0
所以(x-3)2>(x-2)(x-4)
练一练
平方的非负性
目录
2 重要不等式
02
新知探究
如图是在北京召开的第24届国际数学家大会的会标,会标是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去像一个风车,代表中国人民热情好客. 你能在这个图中找出一些相等关系和不等关系吗?
02
新知探究
02
新知2——重要不等式
目录
3 不等式的性质
03
新知探究
问题3 在初中阶段我们学习了不等式的基本性质,
你还记得吗?
1.不等号的两边同时加上(或减去)同一个数,不等号开口方向不变。
2.不等号的两边同时乘(或除以)同一个正数,不等号开口方向不变。
3.不等号的两边同时乘(或除以)同一个负数,不等号开口方向改变。
还有其他性质吗
03
新知3——不等式的性质
1、性质1(可加性) 如果 a > b , 那么 a±c > b±c
3、性质3 (传递性) 如果 a > b , b > c , 那么 a > c
03
新知3——不等式的性质
6、性质6(同向可加性) 如果 a>b , c>d ,那么 a+c >b+d
练一练
ACD
练一练
目录
4 题型
04
题型1-作差法比较大小
例1.完成一项装修工程,请木工需付工资每人50元,请瓦工需付工资每人40元,现有工人工资预算2 000元,设木工x人,瓦工y人,则请工人满足的关系式是
A.5x+4y<200 B.5x+4y≥200C.5x+4y=200 D.5x+4y≤200
√
解 依题意,得50x+40y≤2 000,即5x+4y≤200.
例2.一个两位数,个位数字为x,十位数字为y,且这个两位数大于70,用不等式表示为____________.
10y+x>70
解 ∵该两位数可表示为10y+x,∴10y+x>70.
04
题型1-作差法比较大小
例3 比较2x2+5x+3与x2+4x+2的大小.
∴(2x2+5x+3)-(x2+4x+2)>0,∴2x2+5x+3>x2+4x+2.
例4.设m=2a2+2a+1,n=(a+1)2,则m,n的大小关系是________.
解 ∵m-n=2a2+2a+1-(a+1)2=a2≥0.∴m≥n.
m≥n
04
题型2-不等式性质的应用
例5 对于实数a,b,c,下列选项正确是(D)
√
解 特殊值排除法.
取c=0,则ac2=bc2,故A错.
04
题型3-不等式的证明与求范围
∵a0,ab>0,
而a>b,∴b-a<0,∴ab>0.
04
题型3-不等式的证明与求范围
例7.已知-1≤x+y≤4,且2≤x-y≤3,则z=2x-3y的
取值范围是________.
3≤z≤8
∴3≤z≤8.
课堂小结
A
B
b
x
(B)
A
(b)
x
B
A
b
x
1.两实数大小关系的基本事实
作差法
2.重要不等式
3.不等式性质
本课结束
课后要记得巩固哦!
2.1 等式性质与不等式性质
1 比较两数(式)的大小
目录
2 重要不等式
3 不等式的性质
4 题型
00
引入课题
高与矮
在现实世界和日常生活中,大量存在着相等关系和不等关系,例如多与少、大与小、重与轻、长与短、高与矮、远与近、升与降、涨与跌、不超过和不少于等。类似于这样的问题反映在数量关系上就是相等和不相等,相等用等式表示,不等用不等式表示。
目录
1 比较两数(式)的大小
01
新知探究
问题2你能用不等式或不等式组表示下列问题中的不等关系吗?
01
新知探究
问题2 常见的不等关系下列,你能用文字语言和符号语言表述吗?
文字 语言 大于 大于 等于 小于 小于 等于 至多 至少 不少于 不多于
符号 语言
>
≥
<
≤
≤
≤
≥
≥
问题3 在初中阶段如何比较两个实数的大小关系呢?
还有其他方法吗
x
0
1
2
3
-1
-2
4
5
-3
-4
C
B
A
实数与数轴上的点一一对应,且从左到右依次增大。
01
新知1——比较两数(式)的大小
A
B
b
x
(B)
A
(b)
x
B
A
b
x
1.两实数大小关系的基本事实
0是正数与负数的分界点,它为实数比较大小提供了“标杆”.
作差法
练一练
练一练
例 2.已知a≥1,试比较
和 的大小.
作商法
练一练
例 3. 比较(x-3)2与(x-2)(x-4)的大小.
解:
(x-3)2-(x-2)(x-4)=x2-6x+9-x2+6x-8=1>0
所以(x-3)2>(x-2)(x-4)
练一练
平方的非负性
目录
2 重要不等式
02
新知探究
如图是在北京召开的第24届国际数学家大会的会标,会标是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去像一个风车,代表中国人民热情好客. 你能在这个图中找出一些相等关系和不等关系吗?
02
新知探究
02
新知2——重要不等式
目录
3 不等式的性质
03
新知探究
问题3 在初中阶段我们学习了不等式的基本性质,
你还记得吗?
1.不等号的两边同时加上(或减去)同一个数,不等号开口方向不变。
2.不等号的两边同时乘(或除以)同一个正数,不等号开口方向不变。
3.不等号的两边同时乘(或除以)同一个负数,不等号开口方向改变。
还有其他性质吗
03
新知3——不等式的性质
1、性质1(可加性) 如果 a > b , 那么 a±c > b±c
3、性质3 (传递性) 如果 a > b , b > c , 那么 a > c
03
新知3——不等式的性质
6、性质6(同向可加性) 如果 a>b , c>d ,那么 a+c >b+d
练一练
ACD
练一练
目录
4 题型
04
题型1-作差法比较大小
例1.完成一项装修工程,请木工需付工资每人50元,请瓦工需付工资每人40元,现有工人工资预算2 000元,设木工x人,瓦工y人,则请工人满足的关系式是
A.5x+4y<200 B.5x+4y≥200C.5x+4y=200 D.5x+4y≤200
√
解 依题意,得50x+40y≤2 000,即5x+4y≤200.
例2.一个两位数,个位数字为x,十位数字为y,且这个两位数大于70,用不等式表示为____________.
10y+x>70
解 ∵该两位数可表示为10y+x,∴10y+x>70.
04
题型1-作差法比较大小
例3 比较2x2+5x+3与x2+4x+2的大小.
∴(2x2+5x+3)-(x2+4x+2)>0,∴2x2+5x+3>x2+4x+2.
例4.设m=2a2+2a+1,n=(a+1)2,则m,n的大小关系是________.
解 ∵m-n=2a2+2a+1-(a+1)2=a2≥0.∴m≥n.
m≥n
04
题型2-不等式性质的应用
例5 对于实数a,b,c,下列选项正确是(D)
√
解 特殊值排除法.
取c=0,则ac2=bc2,故A错.
04
题型3-不等式的证明与求范围
∵a
而a>b,∴b-a<0,∴ab>0.
04
题型3-不等式的证明与求范围
例7.已知-1≤x+y≤4,且2≤x-y≤3,则z=2x-3y的
取值范围是________.
3≤z≤8
∴3≤z≤8.
课堂小结
A
B
b
x
(B)
A
(b)
x
B
A
b
x
1.两实数大小关系的基本事实
作差法
2.重要不等式
3.不等式性质
本课结束
课后要记得巩固哦!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
