第六单元多边形的面积基础练习 人教版数学五年级上册(含解析)
文档属性
| 名称 | 第六单元多边形的面积基础练习 人教版数学五年级上册(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 402.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-01 10:59:21 | ||
图片预览



文档简介
/ 让教学更有效 精品试卷 | 数学
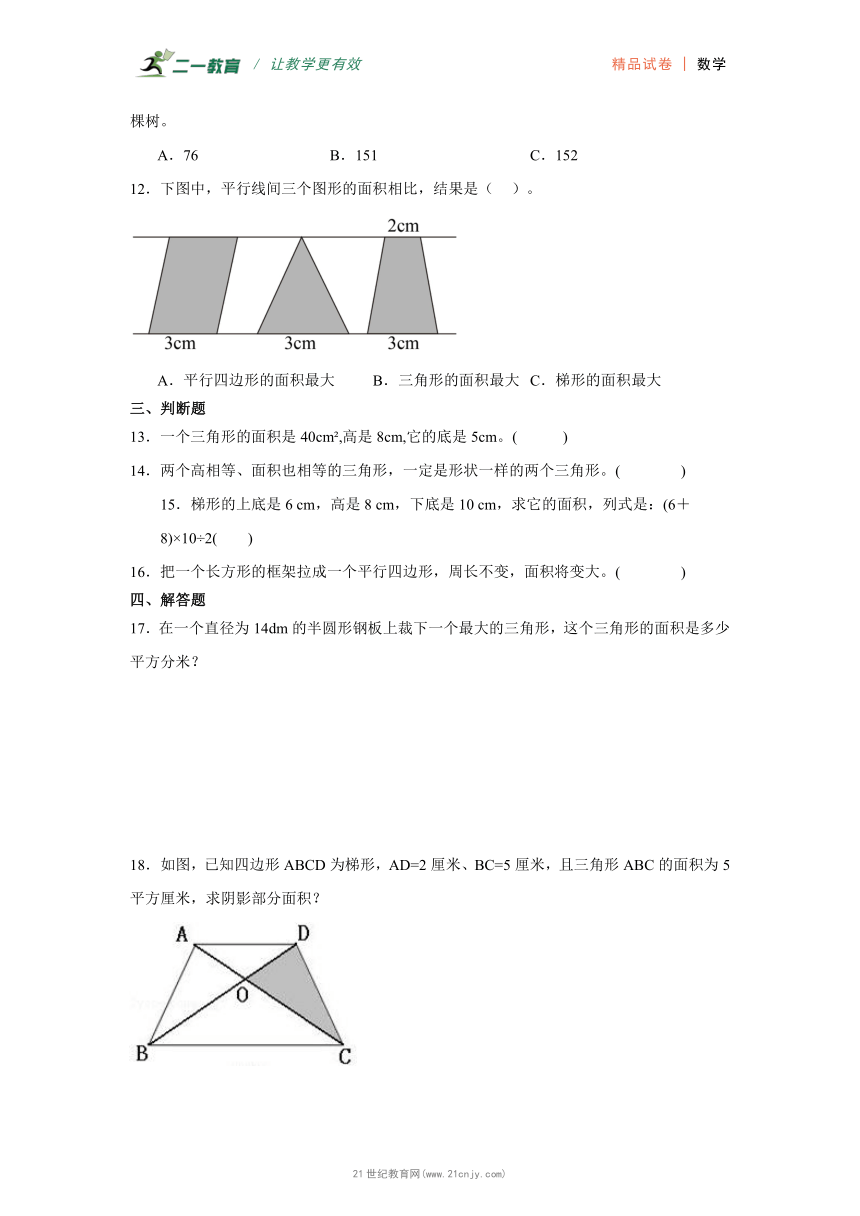
第六单元多边形的面积
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.在中,它的面积是12平方厘米,高6厘米,底是 厘米.
2.一个三角形的底是12厘米,高是6厘米,这个三角形的面积是 平方厘米,与这个三角形等底等高的平行四边形的面积是 平方厘米.21cnjy.com
3.梯形的面积是54平方米,高是6米,上底是8米,下底是 米.
4.一个梯形的上底与下底的和是25厘米,高是8厘米.这个梯形的面积是 .
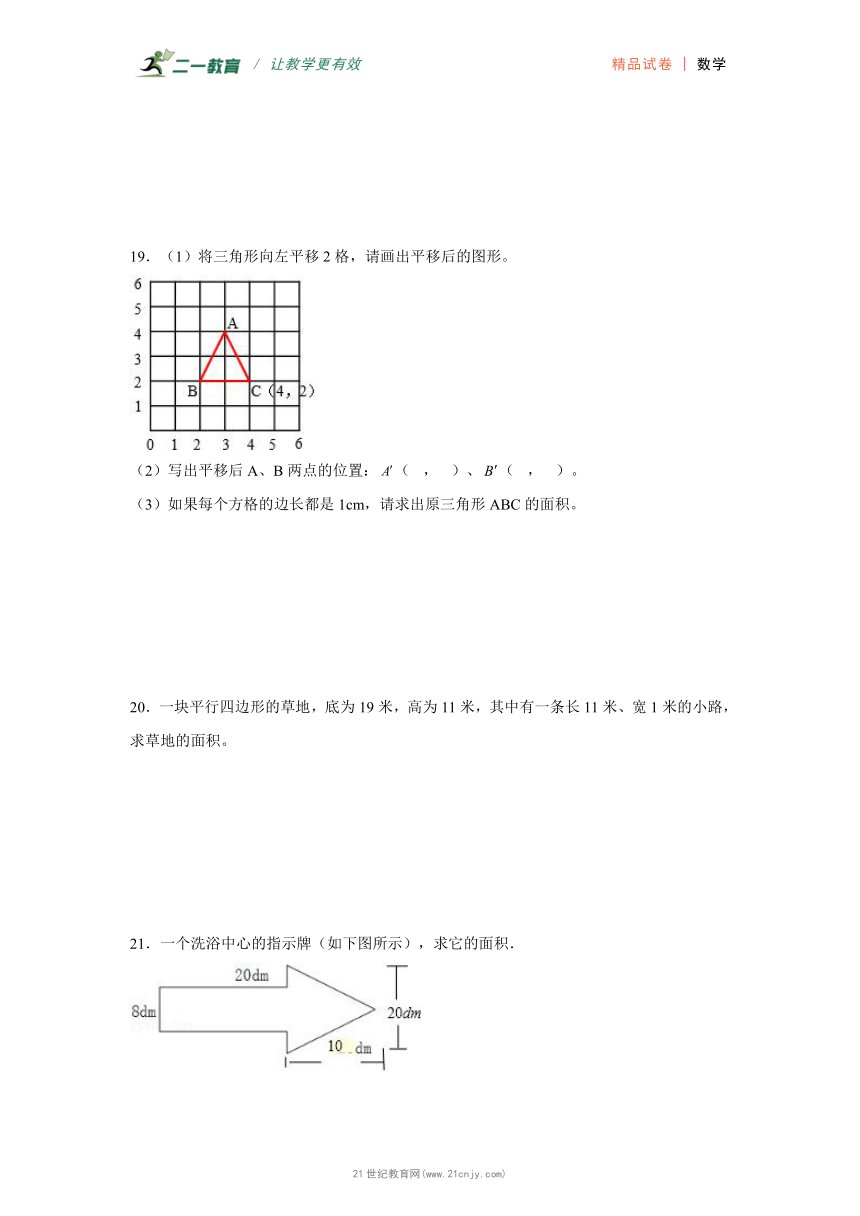
5.一个果园是梯形。它的上底是120米,下底是40米,高是80米。这个果园的面积是 平方米。
6.一个三角形和一个平行四边形的底和高都相等,它的面积比是 .
二、选择题
7.一张梯形手工纸的上底是12cm,下底是20cm,高是8cm。林林要从这张纸里剪一个最大的平行四边形,这个平行四边形的面积是( )平方厘米。www-2-1-cnjy-com
A.48 B.160 C.96
8.在两条平行线之间有3个图形(如图),它们的面积相比,( )。
A.甲的面积最大 B.丙的面积最大 C.一样大
9.一个三角形的底是8 分米,高是6 分米,和它等底等高的平行四边形的面积是( )平方分米.
A.48 B.24 C.16
10.一堆钢管,最底层有15根,最顶层有6根,每相邻两层差1根,这堆钢管共有( )根。
A.210 B.105 C.84
11.在一条长300米的公路两边种树(两端都植),每隔4米种一棵,一共可以种( )棵树。
A.76 B.151 C.152
12.下图中,平行线间三个图形的面积相比,结果是( )。
A.平行四边形的面积最大 B.三角形的面积最大 C.梯形的面积最大
三、判断题
13.一个三角形的面积是40cm ,高是8cm,它的底是5cm。( )
14.两个高相等、面积也相等的三角形,一定是形状一样的两个三角形。( )
15.梯形的上底是6 cm,高是8 cm,下底是10 cm,求它的面积,列式是:(6+8)×10÷2( )2-1-c-n-j-y
16.把一个长方形的框架拉成一个平行四边形,周长不变,面积将变大。( )
四、解答题
17.在一个直径为14dm的半圆形钢板上裁下一个最大的三角形,这个三角形的面积是多少平方分米?
如图,已知四边形ABCD为梯形,AD=2厘米、BC=5厘米,且三角形ABC的面积为5平方厘米,求阴影部分面积?
【版权所有:21教育】
19.(1)将三角形向左平移2格,请画出平移后的图形。
(2)写出平移后A、B两点的位置:( , )、( , )。
(3)如果每个方格的边长都是1cm,请求出原三角形ABC的面积。
20.一块平行四边形的草地,底为19米,高为11米,其中有一条长11米、宽1米的小路,求草地的面积。21教育名师原创作品
一个洗浴中心的指示牌(如下图所示),求它的面积.
参考答案:
1.4
【详解】试题分析:由“三角形的面积=底×高÷2”可得“三角形的高=三角形的面积×2÷底”,三角形的面积和底已知,代入关系式即可求解.21教育网
解:12×2÷6,
=24÷6,
=4(厘米).
答:这个三角形的高是4厘米.
故答案为4.
点评:此题主要考查三角形的面积的计算方法的灵活应用.
2. 36 72
【分析】因为三角形的面积=底×高÷2,平行四边形的面积=底×高,则三角形的面积是与其等底等高的平行四边形面积的一半,据此求解即可.2·1·c·n·j·y
【详解】三角形的面积:12×6÷2,
=72÷2,
=36(平方厘米);
平行四边形的面积:36×2=72(平方厘米);
答:这个三角形的面积是36平方厘米,与这个三角形等底等高的平行四边形的面积是72平方厘米.
故答案为36,72.
3.10
【详解】试题分析:根据梯形的面积计算公式,s=(a+b)h÷2,已知梯形的面积是54平方米,高是6米,上底是8米,求下底是多少米.根据梯形的面积计算方法,用面积乘2除以高,再减上底.由此列式解答.21*cnjy*com
解:54×2÷6﹣8,
=108÷6﹣8,
=18﹣8,
=10(米);
答;下底是10米.
故答案为;10.
点评:此题主要考查梯形的面积计算方法,根据梯形的面积计算方法解决有关的实际问题.
4.100平方厘米
【分析】此题根据公式“梯形的面积=(上底+下底)×高÷2”,进行解答即可.
【详解】25×8÷2
=200÷2
=100(平方厘米)
答:这个梯形的面积是100平方厘米.
故答案为100平方厘米.
5.6400
【分析】根据梯形面积=(上底+下底)×高÷2,列式计算即可。
【详解】(120+40)×80÷2
=160×40
=6400(平方米)
【点睛】关键是掌握梯形的面积公式。
6.1:2
【详解】试题分析:根据题意,一个三角形和一个平行四边形的底和高都相等,,由三角形的面积公式和平行四边形的面积公式,求出它们各自的面积,再根据比的意义求解即可.
解:根据题意,假设底为2,高为1.
三角形的面积=底×高÷2=2×1÷2=1,
平行四边形的面积=底×高=2×1=2,
那么它们的面积比是1:2.
故答案为1:2.
点评:由题意,假设底与高是一个简单具体的数值,根据各自的面积公式算出面积,再根据比的意义求解即可.
7.C
【分析】在梯形里剪最大的平行四边形,平行四边形的底=这个梯形的上底,平行四边形的高=这个梯形的高,根据平行四边形面积=底×高,列式计算即可。21·cn·jy·com
【详解】12×8=96(平方厘米)
这个平行四边形的面积是96平方厘米。
故答案为:C
【点睛】关键是熟悉平行四边形和梯形的特征,掌握并灵活运用平行四边形面积公式。
8.B
【分析】根据“两条平行线间的距离相等”可知,甲、乙、丙三个图形的高相等,设它们的高是hcm。
根据三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,平行四边形的面积=底×高,分别求出甲、乙、丙三个图形的面积,再比较,得出结论。www.21-cn-jy.com
【详解】设甲、乙、丙三个图形的高都是hcm。
甲的面积:6×h÷2=3h(cm2)
乙的面积:
(2+4)×h÷2
=6×h÷2
=3h(cm2)
丙的面积:6×h=6h(cm2)
6h>3h
它们的面积相比,丙的面积最大。
故答案为:B
9.A
【详解】8×6=48(平方分米)
答:和它等底等高的平行四边形的面积是48平方分米;
故选:A.
10.B
【分析】根据题意可知,这堆钢管呈梯形状,根据“梯形的面积=(上底+下底)×高÷2”
解答即可。
【详解】(15+6)×(15-6+1)÷2
=21×10÷2
=105(根)
故答案为:B。
【点睛】明确钢管呈梯形状,熟记梯形的面积计算公式是解答本题的关键。
11.C
【分析】由题意可知,属于两端都植的情况,棵数=间隔数+1,用300÷4+1即可求出一边的植树棵数,再乘2即可求出两边一共的植树棵数。21·世纪*教育网
【详解】(300÷4+1)×2
=76×2
=152(棵);
故答案为:C。
【点睛】明确植树问题中两端都植的特点是解答本题的关键。
12.A
【分析】看图,三个图形的高相等,那么可以假设高为具体的数,比如4cm。平行四边形面积=底×高,三角形面积=底×高÷2,梯形面积=(上底+下底)×高÷2,据此列式求出各个图形的面积,再得出哪个图形的面积最大。21世纪教育网版权所有
【详解】令高为4cm,
平行四边形面积:3×4=12(cm2)
三角形面积:3×4÷2=6(cm2)
梯形面积:
(2+3)×4÷2
=5×4÷2
=10(cm2)
12>10>6,所以,平行四边形的面积最大。
故答案为:A
13.×
【解析】略
14.×
【分析】三角形的面积=底×高÷2,等底、等高的三角形的面积相等,因此高相等、面积也相等的三角形,它们的底也相等;从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底;依此画出等底、等高的两个三角形,然后再判断即可。【来源:21·世纪·教育·网】
【详解】根据分析,画图如下:
由此可知,两个高相等、面积也相等的三角形,不一定是形状一样的两个三角形。
故答案为:×
【点睛】解答此题的关键是要熟练掌握三角形的面积的计算方法。
15.×
【详解】略
16.×
【分析】当长方形被拉成平行四边形后,它的长和宽没变,所以周长不变,但是高变小了,所以面积就变小了。
【详解】因为长方形被拉成平行四边形,周长不变,但是高变小了,所以面积就变小了。
故答案为:×
【点睛】此题主要考查平行四边形易变形的特征及周长和面积公式的灵活应用。
17.49平方分米
【详解】试题分析:由题意可知:这个三角形的底和高分别为半圆的直径和半径,据此即可解答本题.
解:14×(14÷2)÷2,
=14×7÷2,
=49(平方分米);
答:这个三角形的面积是49平方分米.
点评:解答此题的关键是明白:这个三角形的底和高分别为半圆的直径和半径.
18.平方厘米
【详解】试题分析:根据三角形ABC的面积为5平方厘米,BC=5厘米,可以求出三角形ABC的高,即三角形ADC的高,由此即可求出三角形ACD的面积,再根据三角形AOD与三角形BOC相似,得出对应边的比等于对应高的比,求出三角形AOD的高,进而求出三角形AOD的面积,继而求出阴影部分的面积.21*cnjy*com
解:ABC高是:5×2÷5=2(厘米),
ACD面积是:2×2÷2=2(平方厘米),
因为三角形AOD与三角形BOC相似,
设三角形AOD的高为x厘米,则三角形BOC的高为2﹣x厘米,
所以x:(2﹣x)=2:5,
5x=4﹣2x,
7x=4,
x=,
三角形AOD的面积是:2×÷2=(平方厘米),
三角形COD面积是:2﹣=(平方厘米),
答:阴影部分的面积是平方厘米.
点评:本题主要是灵活利用三角形的面积公式与三角形的相似性解决问题.
19.(1)
(2)(1,4),(2,0);
(3)2平方厘米
【分析】(1)根据图形的平移的方法,先把三角形的三个顶点向左平移2格,在顺次连接起来即可得出平移后的三角形;【来源:21cnj*y.co*m】
(2)根据数对表示位置的方法可知:(1,4)、(2,0)。
(3)根据三角形的面积公=底×高÷2,求出面积。
【详解】由分析得,
(1)
(2)平移后A、B两点的位置:(1,4)、(2,0)。
(3)2×2÷2
=4÷2
=2(平方厘米)
【点睛】题考查了数对表示位置以及图形的平移与旋转的方法的灵活应用,注意画图的规范性。
20.198平方米
【分析】草地的面积等于这个底为19米,高为11米的平行四边形的面积,减去长11米、宽1米的小路的面积,由此利用平行四边形与长方形的面积公式即可解答。
【详解】19×11﹣11×1
=209﹣11
=198(平方米)
答:草地的面积是198平方米。
【点睛】根据题干画出图形,即可得出这个组合图形的面积=平行四边形面积-中间长方形的面积。
21.260平方分米
【详解】试题分析:指示牌是由长方形和三角形组成的,根据长方形和三角形的面积公式解答即可.
解:20×8+20×10÷2
=160+100,
=260(平方分米);
答:它的面积是260平方分米.
点评:此题主要考查组合图形面积计算,一般情况把组合图形分成几个规则图形,分别计算出它们的面积合并起来即可.【出处:21教育名师】
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第六单元多边形的面积
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.在中,它的面积是12平方厘米,高6厘米,底是 厘米.
2.一个三角形的底是12厘米,高是6厘米,这个三角形的面积是 平方厘米,与这个三角形等底等高的平行四边形的面积是 平方厘米.21cnjy.com
3.梯形的面积是54平方米,高是6米,上底是8米,下底是 米.
4.一个梯形的上底与下底的和是25厘米,高是8厘米.这个梯形的面积是 .
5.一个果园是梯形。它的上底是120米,下底是40米,高是80米。这个果园的面积是 平方米。
6.一个三角形和一个平行四边形的底和高都相等,它的面积比是 .
二、选择题
7.一张梯形手工纸的上底是12cm,下底是20cm,高是8cm。林林要从这张纸里剪一个最大的平行四边形,这个平行四边形的面积是( )平方厘米。www-2-1-cnjy-com
A.48 B.160 C.96
8.在两条平行线之间有3个图形(如图),它们的面积相比,( )。
A.甲的面积最大 B.丙的面积最大 C.一样大
9.一个三角形的底是8 分米,高是6 分米,和它等底等高的平行四边形的面积是( )平方分米.
A.48 B.24 C.16
10.一堆钢管,最底层有15根,最顶层有6根,每相邻两层差1根,这堆钢管共有( )根。
A.210 B.105 C.84
11.在一条长300米的公路两边种树(两端都植),每隔4米种一棵,一共可以种( )棵树。
A.76 B.151 C.152
12.下图中,平行线间三个图形的面积相比,结果是( )。
A.平行四边形的面积最大 B.三角形的面积最大 C.梯形的面积最大
三、判断题
13.一个三角形的面积是40cm ,高是8cm,它的底是5cm。( )
14.两个高相等、面积也相等的三角形,一定是形状一样的两个三角形。( )
15.梯形的上底是6 cm,高是8 cm,下底是10 cm,求它的面积,列式是:(6+8)×10÷2( )2-1-c-n-j-y
16.把一个长方形的框架拉成一个平行四边形,周长不变,面积将变大。( )
四、解答题
17.在一个直径为14dm的半圆形钢板上裁下一个最大的三角形,这个三角形的面积是多少平方分米?
如图,已知四边形ABCD为梯形,AD=2厘米、BC=5厘米,且三角形ABC的面积为5平方厘米,求阴影部分面积?
【版权所有:21教育】
19.(1)将三角形向左平移2格,请画出平移后的图形。
(2)写出平移后A、B两点的位置:( , )、( , )。
(3)如果每个方格的边长都是1cm,请求出原三角形ABC的面积。
20.一块平行四边形的草地,底为19米,高为11米,其中有一条长11米、宽1米的小路,求草地的面积。21教育名师原创作品
一个洗浴中心的指示牌(如下图所示),求它的面积.
参考答案:
1.4
【详解】试题分析:由“三角形的面积=底×高÷2”可得“三角形的高=三角形的面积×2÷底”,三角形的面积和底已知,代入关系式即可求解.21教育网
解:12×2÷6,
=24÷6,
=4(厘米).
答:这个三角形的高是4厘米.
故答案为4.
点评:此题主要考查三角形的面积的计算方法的灵活应用.
2. 36 72
【分析】因为三角形的面积=底×高÷2,平行四边形的面积=底×高,则三角形的面积是与其等底等高的平行四边形面积的一半,据此求解即可.2·1·c·n·j·y
【详解】三角形的面积:12×6÷2,
=72÷2,
=36(平方厘米);
平行四边形的面积:36×2=72(平方厘米);
答:这个三角形的面积是36平方厘米,与这个三角形等底等高的平行四边形的面积是72平方厘米.
故答案为36,72.
3.10
【详解】试题分析:根据梯形的面积计算公式,s=(a+b)h÷2,已知梯形的面积是54平方米,高是6米,上底是8米,求下底是多少米.根据梯形的面积计算方法,用面积乘2除以高,再减上底.由此列式解答.21*cnjy*com
解:54×2÷6﹣8,
=108÷6﹣8,
=18﹣8,
=10(米);
答;下底是10米.
故答案为;10.
点评:此题主要考查梯形的面积计算方法,根据梯形的面积计算方法解决有关的实际问题.
4.100平方厘米
【分析】此题根据公式“梯形的面积=(上底+下底)×高÷2”,进行解答即可.
【详解】25×8÷2
=200÷2
=100(平方厘米)
答:这个梯形的面积是100平方厘米.
故答案为100平方厘米.
5.6400
【分析】根据梯形面积=(上底+下底)×高÷2,列式计算即可。
【详解】(120+40)×80÷2
=160×40
=6400(平方米)
【点睛】关键是掌握梯形的面积公式。
6.1:2
【详解】试题分析:根据题意,一个三角形和一个平行四边形的底和高都相等,,由三角形的面积公式和平行四边形的面积公式,求出它们各自的面积,再根据比的意义求解即可.
解:根据题意,假设底为2,高为1.
三角形的面积=底×高÷2=2×1÷2=1,
平行四边形的面积=底×高=2×1=2,
那么它们的面积比是1:2.
故答案为1:2.
点评:由题意,假设底与高是一个简单具体的数值,根据各自的面积公式算出面积,再根据比的意义求解即可.
7.C
【分析】在梯形里剪最大的平行四边形,平行四边形的底=这个梯形的上底,平行四边形的高=这个梯形的高,根据平行四边形面积=底×高,列式计算即可。21·cn·jy·com
【详解】12×8=96(平方厘米)
这个平行四边形的面积是96平方厘米。
故答案为:C
【点睛】关键是熟悉平行四边形和梯形的特征,掌握并灵活运用平行四边形面积公式。
8.B
【分析】根据“两条平行线间的距离相等”可知,甲、乙、丙三个图形的高相等,设它们的高是hcm。
根据三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,平行四边形的面积=底×高,分别求出甲、乙、丙三个图形的面积,再比较,得出结论。www.21-cn-jy.com
【详解】设甲、乙、丙三个图形的高都是hcm。
甲的面积:6×h÷2=3h(cm2)
乙的面积:
(2+4)×h÷2
=6×h÷2
=3h(cm2)
丙的面积:6×h=6h(cm2)
6h>3h
它们的面积相比,丙的面积最大。
故答案为:B
9.A
【详解】8×6=48(平方分米)
答:和它等底等高的平行四边形的面积是48平方分米;
故选:A.
10.B
【分析】根据题意可知,这堆钢管呈梯形状,根据“梯形的面积=(上底+下底)×高÷2”
解答即可。
【详解】(15+6)×(15-6+1)÷2
=21×10÷2
=105(根)
故答案为:B。
【点睛】明确钢管呈梯形状,熟记梯形的面积计算公式是解答本题的关键。
11.C
【分析】由题意可知,属于两端都植的情况,棵数=间隔数+1,用300÷4+1即可求出一边的植树棵数,再乘2即可求出两边一共的植树棵数。21·世纪*教育网
【详解】(300÷4+1)×2
=76×2
=152(棵);
故答案为:C。
【点睛】明确植树问题中两端都植的特点是解答本题的关键。
12.A
【分析】看图,三个图形的高相等,那么可以假设高为具体的数,比如4cm。平行四边形面积=底×高,三角形面积=底×高÷2,梯形面积=(上底+下底)×高÷2,据此列式求出各个图形的面积,再得出哪个图形的面积最大。21世纪教育网版权所有
【详解】令高为4cm,
平行四边形面积:3×4=12(cm2)
三角形面积:3×4÷2=6(cm2)
梯形面积:
(2+3)×4÷2
=5×4÷2
=10(cm2)
12>10>6,所以,平行四边形的面积最大。
故答案为:A
13.×
【解析】略
14.×
【分析】三角形的面积=底×高÷2,等底、等高的三角形的面积相等,因此高相等、面积也相等的三角形,它们的底也相等;从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底;依此画出等底、等高的两个三角形,然后再判断即可。【来源:21·世纪·教育·网】
【详解】根据分析,画图如下:
由此可知,两个高相等、面积也相等的三角形,不一定是形状一样的两个三角形。
故答案为:×
【点睛】解答此题的关键是要熟练掌握三角形的面积的计算方法。
15.×
【详解】略
16.×
【分析】当长方形被拉成平行四边形后,它的长和宽没变,所以周长不变,但是高变小了,所以面积就变小了。
【详解】因为长方形被拉成平行四边形,周长不变,但是高变小了,所以面积就变小了。
故答案为:×
【点睛】此题主要考查平行四边形易变形的特征及周长和面积公式的灵活应用。
17.49平方分米
【详解】试题分析:由题意可知:这个三角形的底和高分别为半圆的直径和半径,据此即可解答本题.
解:14×(14÷2)÷2,
=14×7÷2,
=49(平方分米);
答:这个三角形的面积是49平方分米.
点评:解答此题的关键是明白:这个三角形的底和高分别为半圆的直径和半径.
18.平方厘米
【详解】试题分析:根据三角形ABC的面积为5平方厘米,BC=5厘米,可以求出三角形ABC的高,即三角形ADC的高,由此即可求出三角形ACD的面积,再根据三角形AOD与三角形BOC相似,得出对应边的比等于对应高的比,求出三角形AOD的高,进而求出三角形AOD的面积,继而求出阴影部分的面积.21*cnjy*com
解:ABC高是:5×2÷5=2(厘米),
ACD面积是:2×2÷2=2(平方厘米),
因为三角形AOD与三角形BOC相似,
设三角形AOD的高为x厘米,则三角形BOC的高为2﹣x厘米,
所以x:(2﹣x)=2:5,
5x=4﹣2x,
7x=4,
x=,
三角形AOD的面积是:2×÷2=(平方厘米),
三角形COD面积是:2﹣=(平方厘米),
答:阴影部分的面积是平方厘米.
点评:本题主要是灵活利用三角形的面积公式与三角形的相似性解决问题.
19.(1)
(2)(1,4),(2,0);
(3)2平方厘米
【分析】(1)根据图形的平移的方法,先把三角形的三个顶点向左平移2格,在顺次连接起来即可得出平移后的三角形;【来源:21cnj*y.co*m】
(2)根据数对表示位置的方法可知:(1,4)、(2,0)。
(3)根据三角形的面积公=底×高÷2,求出面积。
【详解】由分析得,
(1)
(2)平移后A、B两点的位置:(1,4)、(2,0)。
(3)2×2÷2
=4÷2
=2(平方厘米)
【点睛】题考查了数对表示位置以及图形的平移与旋转的方法的灵活应用,注意画图的规范性。
20.198平方米
【分析】草地的面积等于这个底为19米,高为11米的平行四边形的面积,减去长11米、宽1米的小路的面积,由此利用平行四边形与长方形的面积公式即可解答。
【详解】19×11﹣11×1
=209﹣11
=198(平方米)
答:草地的面积是198平方米。
【点睛】根据题干画出图形,即可得出这个组合图形的面积=平行四边形面积-中间长方形的面积。
21.260平方分米
【详解】试题分析:指示牌是由长方形和三角形组成的,根据长方形和三角形的面积公式解答即可.
解:20×8+20×10÷2
=160+100,
=260(平方分米);
答:它的面积是260平方分米.
点评:此题主要考查组合图形面积计算,一般情况把组合图形分成几个规则图形,分别计算出它们的面积合并起来即可.【出处:21教育名师】
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
