苏科版八年级数学下册试题 第7章《数据的收集、整理、描述》单元复习卷(含答案)
文档属性
| 名称 | 苏科版八年级数学下册试题 第7章《数据的收集、整理、描述》单元复习卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 479.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-01 18:35:06 | ||
图片预览




文档简介
第7章《数据的收集、整理、描述》单元复习卷
一、单选题(共10题,每题4分,共40分)
1.下列调查中,适合用全面调查的是( )
A.了解某市居民日平均用水量 B.了解一批炮弹的杀伤半径
C.了解我校师生的核酸检测结果 D.了解全国青少年喜欢的电视节目
2.精准扶贫是全面建成小康社会的重要保障,某乡为了解果农的年收入情况,从全乡果农中随机抽取50户果农进行调查,这50户果农的年收入是( )
A.样本 B.样本容量 C.个体 D.总体
3.为了了解某市参加中考的名学生的体重情况,抽查了其中1600名学生的体重进行统计分析.下列叙述正确的是( )
A.名学生是总体 B.名学生的体重是总体的一个样本
C.每名学生是总体的一个个体 D.样本容量是名
4.统计全国每天新冠肺炎疫情变化情况,应选择( )
A.统计表 B.条形统计图 C.折线统计图 D.扇形统计图
5.深圳市某学校对学生上学方式进行一次抽样调查,并根据调查结果绘制了不完整的扇形统计图,其中“其他”部分对应的圆心角是36°,则“步行”部分所占百分比是( )
A.64% B.35% C.36% D.40%
6.为调查某中学学生对“五项管理”的了解程度,盘州市教育局进行了抽样调查,以下样本最具有代表性的是( )
A.九年级的学生对“五项管理”的了解程度
B.全校女生对“五项管理”的了解程度
C.在篮球场上打篮球的学生对“五项管理”的了解程度
D.每班学号尾号为5的学生对“五项管理”的了解程度
7.一组数据的最大值与最小值的差为80,若确定组距为9,则分成组数为( )
A.7 B.8 C.9 D.10
8.小明调查了某地1月份一周的最低气温(单位:℃),分别是-2,0,3,-1,1,0,2,其中0℃以上(不含0℃)出现的频数是( )
A.2 B.3 C.4 D.5
9.小明统计了他家今年5月份打电话的次数及通话时间,并列出了如下的频数分布表:
通话时间 x/min 0频数 (通话次数) 20 16 9 5
则通话时间不超过15 min的频率为( )
A.0.1 B.0.4 C.0.5 D.0.9
10.为了解某一路口某一时刻的汽车流量,小明同学10天中在同一时段统计该路口的汽车数量(单位:辆),将统计结果绘制成如下折线统计图:
由此估计一个月(30天)该时段通过该路口的汽车数量超过200辆的天数为( )
A.9 B.10 C.12 D.15
二、填空题(共8题,每题4分,共32分)
11.以下调查适合作抽样调查的是__________;适合作普查的是 __________(只须填序号)
①了解全国食用盐加碘的情况. ②对七年级2班学生睡眠时间的调查.
③对构成人造卫星零部件的检查.④对一个城市的空气质量标准的检测.
12.为了解某区六年级8000名学生中会游泳的学生人数,随机调查了其中500名学牛,结果有200名学生会游泳,那么估计该区会游泳的六年级学生人数为________.
13.为了了解居民对我市“五城联创”的知晓情况,某街道办从辖区居民中随机选取了部分居民进行调查,并将调查结果绘制成如图所示的扇形图.若该辖区约有居民人,则可以估计其中对“五城联创”“非常清楚”的居民约有____________人
14.在一个不透明的口袋中,装有7个红球和3个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球试验发现,摸到黄球的频率是_____________.
15.一个圆形转盘分成3个区域,分别涂上红色、绿色、黄色.小明转动到红色的频数为20,频率为40%,则小明共转动转盘_________次.
16.为了了解七年级学生的体育锻炼时间,小华调查了某班45名同学一周参加体育锻炼的时间,并把它绘制成频数分布直方图(每组含最小值,不含最大值).由图可知,一周参加体育锻炼时间大于等于6小时的有____________人.
17.如图是某地2月18日到23日浓度和空气质量的统计图(当不大于100时称空气质量为“优良”).由图可得下列说法:①18日的浓度最低;②21日的浓度最高;③这六天中有4天空气质量为“优良”;④空气质量指数与浓度有关.其中正确的是________(填序号即可)
18.为了了解某地初二年级男生的身高情况,某班40名学生的身高如下表,则m的值为____.
分组 147.5~155.5 155.5~163.5 163.5~171.5 171.5~179.5
频数 6 11 m
频率 0.45
三、解答题(58分)
19.(8分)某专业户要出售300只羊,现在市场上羊的价格为每千克11元,为了估计这300只羊能卖多少钱,试问:
(1)对于上述问题你认为适用___________.(填“普查”或“抽样调查”)
(2)该专业户从口随机抽取了5只羊,称得它们的质量(单位:千克)如下:26,31,32 ,36,37
①在这个问题中,总体、个体和样本各是___________,___________,___________.
②通过上述数据,你能估算出这300只羊能卖多少钱吗?
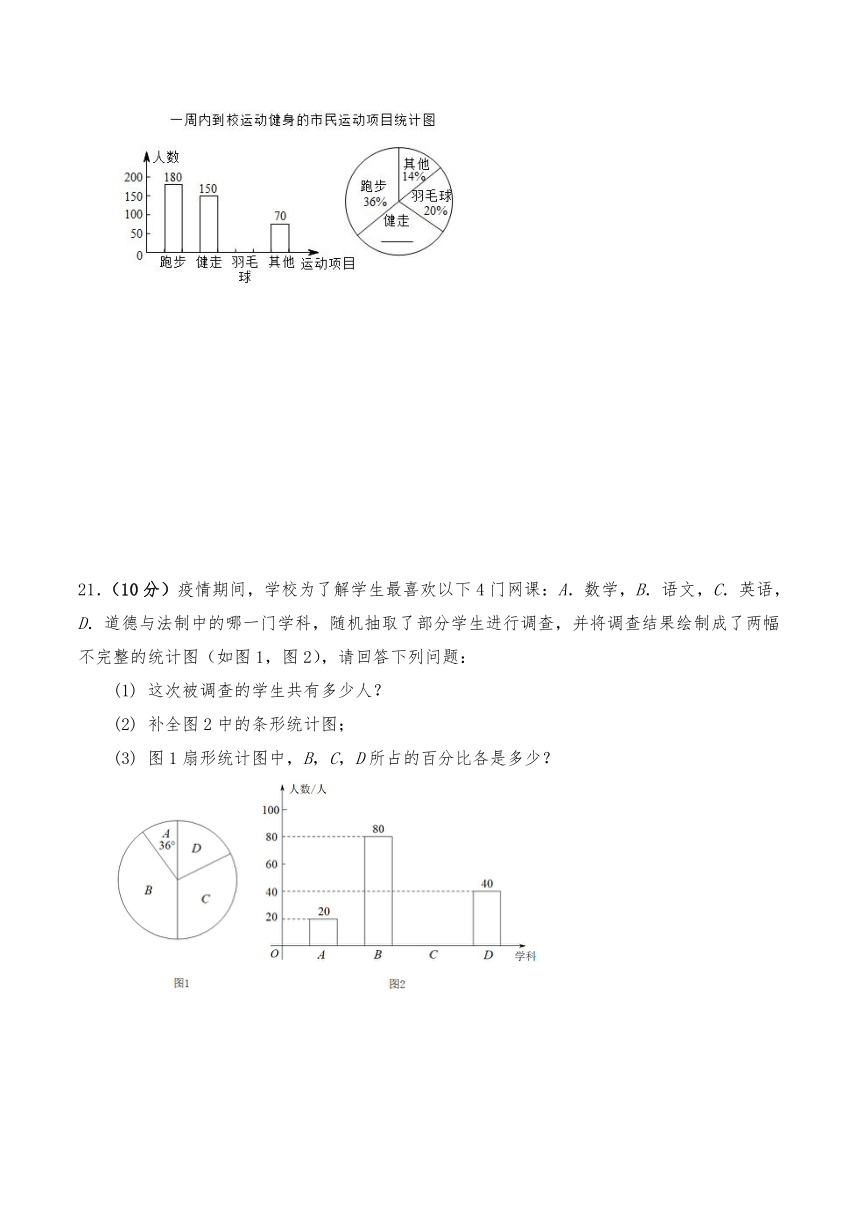
20.(10分)某校体育设施向社会免费开放,对一周内到校运动健身的市民人数进行了统计,并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
(1) 一周内到校运动健身的市民总人数为多少?
(2) 补全条形统计图与扇形统计图;
(3) 为了给运动健身的市民提供更多的便利,你认为学校可以在哪些运动项目的场地加大投入?请结合数据说明理由.
21.(10分)疫情期间,学校为了解学生最喜欢以下4门网课:A.数学,B.语文,C.英语,D.道德与法制中的哪一门学科,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图(如图1,图2),请回答下列问题:
(1) 这次被调查的学生共有多少人?
(2) 补全图2中的条形统计图;
(3) 图1扇形统计图中,B,C,D所占的百分比各是多少?
22.(10分)为弘扬中华传统文化,某校组织八年级800名学生参加汉字听写大赛为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,得到如下所示的模数分布表:
分数段 50.5~60.5 60.5~70.5 70.5~80.5 80.5~90.5 90.5~100.5
频数 16 30 50 m 24
所占百分比 8% 15% 25% 40% n
请根据尚未完成的表格,解答下列问题:
本次抽样调查的样本容量为_____,表中m=_____.
补全图中所示的频数分布直方图.
若成绩超过80分为优秀,则该校八年级学生中汉字听写能力优秀的约有多少人
23.(10分)某校举办了首届“英语原创演讲比赛”,经选拔后有若干名学生参加决赛,根据测试成绩(成绩都不低于 60 分)绘制出如下两幅不完整的统计图表,请根据统计图表提供的信息完成下列各题.
表a:
分数段 60-70 70-80 80-90 90-100
频数 6 19 m 5
频率 15% n 25% 12.5%
参加决赛的学生有 名,请将图b补充完整;
表a中的m= ,n= ;
如果测试成绩不低于80分为优秀,那么本次测试的优秀率是 .
24.(10分)某学校在本学期开展数学拓展活动,为了解开展数学拓展活动后学生不同阶段的学习效果,决定随机抽取七年级部分学生进行两次跟踪测评(两次随机抽取的学生人数相同),第一次是开展数学拓展活动初期的学习质量测评,第二次是开展数学拓展活动个月后的学习质量测评.根据测评的数学成绩制作了第一次测评的数学成绩频数分布直方图(如图,每一组包括左边端点,不包括右边端点)和第二次测评的数学成绩频数分布表(如表).
第二次测评的数学成绩频数分布表:
成绩
频数
根据以上图表信息,完成下列问题:
第一次测评的数学成绩频数分布直方图
(1)______;
(2)若分及以上为优秀.
①开展数学拓展活动个月后,请估计该校名七年级学生数学成绩优秀的人数;
②请分别计算两次测评数学成绩的优秀率,并对开展数学拓展活动的效果进行分析.
答案
一、单选题
1.C
【分析】分别根据普查和抽样调查适宜的条件对各选项进行逐一分析解答即可.
解:A.了解某市居民日平均用水量,适合用抽样调查;
B.了解一批炮弹的杀伤半径,具有一定的破坏性,适合用抽样调查;
C.了解我校师生的核酸检测结果,适合用全面调查;
D.了解全国青少年喜欢的电视节目,适合用抽样调查.
故选:C.
2.A
【分析】从总体中取出的一部分个体叫做这个总体的一个样本,据此可得结论.
解:某乡为了解果农的年收入情况,从全乡果农中随机抽取50户果农进行调查,这50户果农的年收入是样本,
故选:A.
3.B
【分析】根据总体、个体、样本、样本容量的概念进行逐项判断即可.
解:A、名学生的体重是总体,原叙述错误,不符合题意;
B、名学生的体重是总体的一个样本,原叙述正确,符合题意;
C、每名学生的体重是总体的一个个体,原叙述错误,不符合题意;
D、样本容量是,原叙述错误,不符合题意,
故选:B.
4.C
【分析】根据常用的几种统计图反映数据的不同特征结合实际来选择.
解:统计全国每天新冠肺炎疫情变化情况,应选择折线统计图.
故选:C.
5.D
【分析】先求出“其他”部分所占百分比,再用1减去35%,再减去15%与“其他”部分所占百分比,即可求解.
解:∵“其他”部分对应的圆心角是36°,
∴“其他”部分所占百分比是,
∴“步行”部分所占百分比是.
故选:D.
6.D
【分析】抽取样本注意事项就是要考虑样本具有广泛性与代表性,所谓代表性,就是抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
解:由题意知最具代表性的是每班学号尾号为5的学生对“五项管理”的了解程度,而抽取九年级的学生、全校女生及在篮球场打篮球的学生对社会主义核心价值观的了解程度都过于片面,不具备代表性,故D正确.
故选:D.
7.C
【分析】根据组数=(最大值-最小值)÷组距计算,注意小数部分要进位.
解:在样本数据中最大值与最小值的差为80,已知组距为9,那么由于,故可以分成9组.
故选:C.
8.B
【分析】数一下大于0的数据的个数即可.
解:高于0℃的数据有3,1,2共计3个,选项B符合题意,
故选B.
9.D
【分析】用不超过15分钟的通话时间除以所有的通话时间即可求得通话时间不超过15分钟的频率.
解:∵不超过15分钟的通话次数为20+16+9=45次,通话总次数为20+16+9+5=50次,
∴通话时间不超过15min的频率为=0.9,
故选D.
10.C
解:试题分析:由图可知,10天中在同一时段通过该路口的汽车数量超过200辆的有4天,频率为:=0.4,所以估计一个月(30天)该时段通过该路口的汽车数量超过200辆的天数为:30×0.4=12(天).故选C.
二、填空题
11. ①④ ②③
【分析】根据全面调查和抽样调查的特点对选项逐一分析即可.
解:①了解全国食用盐加碘的情况,适合抽样调查;
②对七年级2班学生睡眠时间的调查,范围较小,适合全面调查;
③对构成人造卫星零部件的检查,事关重大,适合全面调查;
④对一个城市的空气质量标准的检测,适合抽样调查;
故答案为:①④;②③.
12.3200
【分析】用总人数乘以样本中会游泳的人数所占比例即可.
解:估计该区会游泳的六年级学生人数为
(人),
故答案为:3200.
13.2700
【分析】先求“清楚”的所占的百分比,再求“非常清楚”所占的百分比,然后直接计算可得答案.
解:由扇形图知:“清楚”的占 ,
所以:“非常清楚”的占: ,
所以:估计其中对“五城联创”“非常清楚”的居民约有人,
故答案为:2700.
14.
【分析】利用黄球的个数除以总的个数即可求出摸到黄球的频率.
解:根据题意得:通过大量重复摸球试验发现,摸到黄球的频率是.
故答案为:
15.50
【分析】根据频率=频数÷总次数,进行计算即可解答.
解:由题意得:
20÷40%=50,
∴小明共转动转盘50次,
故答案为:50.
16.14
【分析】由频数分布直方图可知锻炼时间大于等于6小时的人数为人.
解:由图可知,一周参加体育锻炼时间大于等于6小时的人数是(人),
故答案为:14
17.①②③④
【分析】根据折线统计图提供的信息,逐一分析,即可解答.
解:由统计图可知18日的浓度最低,故①正确;
由统计图可知21日的浓度最高,故②正确;
由统计图可知18日,19日,20日,23日的不大于100,21日和22日的大于100,
∴这六天中有4天空气质量为“优良”,故③正确;
比较两图可知,浓度值越小,空气质量指数越低,故④正确;
故答案为:①②③④.
18.5
【分析】根据频数、频率与总数之间的关系求解即可.
解:由表可得:163.5~171.5组的频数为:40×0.45=18,
∴m=40-6-11-18=5,
故答案为:5.
三、解答题
19.
解:(1)因为羊的头数太多,不宜采用全面调查方式去调查,应先用省时省力的方式采用抽样调查;
故答案为:抽样调查
(2)由题意可知,总体是300羊的质量;个体是每只羊的质量;样本是所抽取的5只羊的质量;
故答案为:300只羊的质量,每只羊的质量,所抽取的5只羊的质量
②(千克),
(元).
即估计这300只羊能卖106920元.
20.
(1)解:(人),
∴一周内到校运动健身的市民总人数为500人;
(2)羽毛球的人数为人,
健走的百分比为,
补全统计图如下:
(3)根据统计图给出的数据,得出结论:跑步和健走占比是总体的,
所以我认为应加大跑步和健走的项目的投入.
21.
解:(1)这次被调查的学生人数为(人).
(2)C学科人数为200﹣(20+80+40)=60(人),
补全图形如下:
(3)扇形统计图中B学科所占的百分比是,
C学科所占的百分比是,
D学科所占的百分比是.
22.
解:样本容量=,,
如下图所示:
由题意可得,
超过80分的人数比有:,
优秀人数为:人.
答:该校八年级学生中汉字听写能力优秀的约有416人.
23.
解:(1)根据图a可知,分数60-70之间的人数有6人,频率为15%,
所以参加决赛的学生总数为人,
∵80-90分段的频率为25%,
∴80-90分段的频数为人,
故答案为:40.
补充图b如下:
(2)根据(1)问中已求出的80-90分段的频数10即为m,
从表a可知,70-80分段人数为19,
所以,
故答案为:10;47.5%.
(3)由表a可知,80分以上人数有10+5=15人,
所以优秀率=,
故答案为:37.5%.
24.
解:(1)由第一次测评的数学成绩频数分布直方图可知参与总人数为:
(人),
根据两次开展数学拓展活动的人数相同,
,
故答案是:;
(2)①根据第二次测评的数学成绩频数分布表,
可知分及以上人数为:(人),
优秀率为:,
该校名七年级学生数学成绩优秀的人数为:(人);
②根据第一次测评的数学成绩频数分布直方图,
可知分及以上人数为:(人),
优秀率为:,
由(2)①得第二次测评的数学成绩优秀率为:,
,
开展数学拓展活动对学生的学习质量有提升作用.
一、单选题(共10题,每题4分,共40分)
1.下列调查中,适合用全面调查的是( )
A.了解某市居民日平均用水量 B.了解一批炮弹的杀伤半径
C.了解我校师生的核酸检测结果 D.了解全国青少年喜欢的电视节目
2.精准扶贫是全面建成小康社会的重要保障,某乡为了解果农的年收入情况,从全乡果农中随机抽取50户果农进行调查,这50户果农的年收入是( )
A.样本 B.样本容量 C.个体 D.总体
3.为了了解某市参加中考的名学生的体重情况,抽查了其中1600名学生的体重进行统计分析.下列叙述正确的是( )
A.名学生是总体 B.名学生的体重是总体的一个样本
C.每名学生是总体的一个个体 D.样本容量是名
4.统计全国每天新冠肺炎疫情变化情况,应选择( )
A.统计表 B.条形统计图 C.折线统计图 D.扇形统计图
5.深圳市某学校对学生上学方式进行一次抽样调查,并根据调查结果绘制了不完整的扇形统计图,其中“其他”部分对应的圆心角是36°,则“步行”部分所占百分比是( )
A.64% B.35% C.36% D.40%
6.为调查某中学学生对“五项管理”的了解程度,盘州市教育局进行了抽样调查,以下样本最具有代表性的是( )
A.九年级的学生对“五项管理”的了解程度
B.全校女生对“五项管理”的了解程度
C.在篮球场上打篮球的学生对“五项管理”的了解程度
D.每班学号尾号为5的学生对“五项管理”的了解程度
7.一组数据的最大值与最小值的差为80,若确定组距为9,则分成组数为( )
A.7 B.8 C.9 D.10
8.小明调查了某地1月份一周的最低气温(单位:℃),分别是-2,0,3,-1,1,0,2,其中0℃以上(不含0℃)出现的频数是( )
A.2 B.3 C.4 D.5
9.小明统计了他家今年5月份打电话的次数及通话时间,并列出了如下的频数分布表:
通话时间 x/min 0
则通话时间不超过15 min的频率为( )
A.0.1 B.0.4 C.0.5 D.0.9
10.为了解某一路口某一时刻的汽车流量,小明同学10天中在同一时段统计该路口的汽车数量(单位:辆),将统计结果绘制成如下折线统计图:
由此估计一个月(30天)该时段通过该路口的汽车数量超过200辆的天数为( )
A.9 B.10 C.12 D.15
二、填空题(共8题,每题4分,共32分)
11.以下调查适合作抽样调查的是__________;适合作普查的是 __________(只须填序号)
①了解全国食用盐加碘的情况. ②对七年级2班学生睡眠时间的调查.
③对构成人造卫星零部件的检查.④对一个城市的空气质量标准的检测.
12.为了解某区六年级8000名学生中会游泳的学生人数,随机调查了其中500名学牛,结果有200名学生会游泳,那么估计该区会游泳的六年级学生人数为________.
13.为了了解居民对我市“五城联创”的知晓情况,某街道办从辖区居民中随机选取了部分居民进行调查,并将调查结果绘制成如图所示的扇形图.若该辖区约有居民人,则可以估计其中对“五城联创”“非常清楚”的居民约有____________人
14.在一个不透明的口袋中,装有7个红球和3个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球试验发现,摸到黄球的频率是_____________.
15.一个圆形转盘分成3个区域,分别涂上红色、绿色、黄色.小明转动到红色的频数为20,频率为40%,则小明共转动转盘_________次.
16.为了了解七年级学生的体育锻炼时间,小华调查了某班45名同学一周参加体育锻炼的时间,并把它绘制成频数分布直方图(每组含最小值,不含最大值).由图可知,一周参加体育锻炼时间大于等于6小时的有____________人.
17.如图是某地2月18日到23日浓度和空气质量的统计图(当不大于100时称空气质量为“优良”).由图可得下列说法:①18日的浓度最低;②21日的浓度最高;③这六天中有4天空气质量为“优良”;④空气质量指数与浓度有关.其中正确的是________(填序号即可)
18.为了了解某地初二年级男生的身高情况,某班40名学生的身高如下表,则m的值为____.
分组 147.5~155.5 155.5~163.5 163.5~171.5 171.5~179.5
频数 6 11 m
频率 0.45
三、解答题(58分)
19.(8分)某专业户要出售300只羊,现在市场上羊的价格为每千克11元,为了估计这300只羊能卖多少钱,试问:
(1)对于上述问题你认为适用___________.(填“普查”或“抽样调查”)
(2)该专业户从口随机抽取了5只羊,称得它们的质量(单位:千克)如下:26,31,32 ,36,37
①在这个问题中,总体、个体和样本各是___________,___________,___________.
②通过上述数据,你能估算出这300只羊能卖多少钱吗?
20.(10分)某校体育设施向社会免费开放,对一周内到校运动健身的市民人数进行了统计,并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
(1) 一周内到校运动健身的市民总人数为多少?
(2) 补全条形统计图与扇形统计图;
(3) 为了给运动健身的市民提供更多的便利,你认为学校可以在哪些运动项目的场地加大投入?请结合数据说明理由.
21.(10分)疫情期间,学校为了解学生最喜欢以下4门网课:A.数学,B.语文,C.英语,D.道德与法制中的哪一门学科,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图(如图1,图2),请回答下列问题:
(1) 这次被调查的学生共有多少人?
(2) 补全图2中的条形统计图;
(3) 图1扇形统计图中,B,C,D所占的百分比各是多少?
22.(10分)为弘扬中华传统文化,某校组织八年级800名学生参加汉字听写大赛为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,得到如下所示的模数分布表:
分数段 50.5~60.5 60.5~70.5 70.5~80.5 80.5~90.5 90.5~100.5
频数 16 30 50 m 24
所占百分比 8% 15% 25% 40% n
请根据尚未完成的表格,解答下列问题:
本次抽样调查的样本容量为_____,表中m=_____.
补全图中所示的频数分布直方图.
若成绩超过80分为优秀,则该校八年级学生中汉字听写能力优秀的约有多少人
23.(10分)某校举办了首届“英语原创演讲比赛”,经选拔后有若干名学生参加决赛,根据测试成绩(成绩都不低于 60 分)绘制出如下两幅不完整的统计图表,请根据统计图表提供的信息完成下列各题.
表a:
分数段 60-70 70-80 80-90 90-100
频数 6 19 m 5
频率 15% n 25% 12.5%
参加决赛的学生有 名,请将图b补充完整;
表a中的m= ,n= ;
如果测试成绩不低于80分为优秀,那么本次测试的优秀率是 .
24.(10分)某学校在本学期开展数学拓展活动,为了解开展数学拓展活动后学生不同阶段的学习效果,决定随机抽取七年级部分学生进行两次跟踪测评(两次随机抽取的学生人数相同),第一次是开展数学拓展活动初期的学习质量测评,第二次是开展数学拓展活动个月后的学习质量测评.根据测评的数学成绩制作了第一次测评的数学成绩频数分布直方图(如图,每一组包括左边端点,不包括右边端点)和第二次测评的数学成绩频数分布表(如表).
第二次测评的数学成绩频数分布表:
成绩
频数
根据以上图表信息,完成下列问题:
第一次测评的数学成绩频数分布直方图
(1)______;
(2)若分及以上为优秀.
①开展数学拓展活动个月后,请估计该校名七年级学生数学成绩优秀的人数;
②请分别计算两次测评数学成绩的优秀率,并对开展数学拓展活动的效果进行分析.
答案
一、单选题
1.C
【分析】分别根据普查和抽样调查适宜的条件对各选项进行逐一分析解答即可.
解:A.了解某市居民日平均用水量,适合用抽样调查;
B.了解一批炮弹的杀伤半径,具有一定的破坏性,适合用抽样调查;
C.了解我校师生的核酸检测结果,适合用全面调查;
D.了解全国青少年喜欢的电视节目,适合用抽样调查.
故选:C.
2.A
【分析】从总体中取出的一部分个体叫做这个总体的一个样本,据此可得结论.
解:某乡为了解果农的年收入情况,从全乡果农中随机抽取50户果农进行调查,这50户果农的年收入是样本,
故选:A.
3.B
【分析】根据总体、个体、样本、样本容量的概念进行逐项判断即可.
解:A、名学生的体重是总体,原叙述错误,不符合题意;
B、名学生的体重是总体的一个样本,原叙述正确,符合题意;
C、每名学生的体重是总体的一个个体,原叙述错误,不符合题意;
D、样本容量是,原叙述错误,不符合题意,
故选:B.
4.C
【分析】根据常用的几种统计图反映数据的不同特征结合实际来选择.
解:统计全国每天新冠肺炎疫情变化情况,应选择折线统计图.
故选:C.
5.D
【分析】先求出“其他”部分所占百分比,再用1减去35%,再减去15%与“其他”部分所占百分比,即可求解.
解:∵“其他”部分对应的圆心角是36°,
∴“其他”部分所占百分比是,
∴“步行”部分所占百分比是.
故选:D.
6.D
【分析】抽取样本注意事项就是要考虑样本具有广泛性与代表性,所谓代表性,就是抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
解:由题意知最具代表性的是每班学号尾号为5的学生对“五项管理”的了解程度,而抽取九年级的学生、全校女生及在篮球场打篮球的学生对社会主义核心价值观的了解程度都过于片面,不具备代表性,故D正确.
故选:D.
7.C
【分析】根据组数=(最大值-最小值)÷组距计算,注意小数部分要进位.
解:在样本数据中最大值与最小值的差为80,已知组距为9,那么由于,故可以分成9组.
故选:C.
8.B
【分析】数一下大于0的数据的个数即可.
解:高于0℃的数据有3,1,2共计3个,选项B符合题意,
故选B.
9.D
【分析】用不超过15分钟的通话时间除以所有的通话时间即可求得通话时间不超过15分钟的频率.
解:∵不超过15分钟的通话次数为20+16+9=45次,通话总次数为20+16+9+5=50次,
∴通话时间不超过15min的频率为=0.9,
故选D.
10.C
解:试题分析:由图可知,10天中在同一时段通过该路口的汽车数量超过200辆的有4天,频率为:=0.4,所以估计一个月(30天)该时段通过该路口的汽车数量超过200辆的天数为:30×0.4=12(天).故选C.
二、填空题
11. ①④ ②③
【分析】根据全面调查和抽样调查的特点对选项逐一分析即可.
解:①了解全国食用盐加碘的情况,适合抽样调查;
②对七年级2班学生睡眠时间的调查,范围较小,适合全面调查;
③对构成人造卫星零部件的检查,事关重大,适合全面调查;
④对一个城市的空气质量标准的检测,适合抽样调查;
故答案为:①④;②③.
12.3200
【分析】用总人数乘以样本中会游泳的人数所占比例即可.
解:估计该区会游泳的六年级学生人数为
(人),
故答案为:3200.
13.2700
【分析】先求“清楚”的所占的百分比,再求“非常清楚”所占的百分比,然后直接计算可得答案.
解:由扇形图知:“清楚”的占 ,
所以:“非常清楚”的占: ,
所以:估计其中对“五城联创”“非常清楚”的居民约有人,
故答案为:2700.
14.
【分析】利用黄球的个数除以总的个数即可求出摸到黄球的频率.
解:根据题意得:通过大量重复摸球试验发现,摸到黄球的频率是.
故答案为:
15.50
【分析】根据频率=频数÷总次数,进行计算即可解答.
解:由题意得:
20÷40%=50,
∴小明共转动转盘50次,
故答案为:50.
16.14
【分析】由频数分布直方图可知锻炼时间大于等于6小时的人数为人.
解:由图可知,一周参加体育锻炼时间大于等于6小时的人数是(人),
故答案为:14
17.①②③④
【分析】根据折线统计图提供的信息,逐一分析,即可解答.
解:由统计图可知18日的浓度最低,故①正确;
由统计图可知21日的浓度最高,故②正确;
由统计图可知18日,19日,20日,23日的不大于100,21日和22日的大于100,
∴这六天中有4天空气质量为“优良”,故③正确;
比较两图可知,浓度值越小,空气质量指数越低,故④正确;
故答案为:①②③④.
18.5
【分析】根据频数、频率与总数之间的关系求解即可.
解:由表可得:163.5~171.5组的频数为:40×0.45=18,
∴m=40-6-11-18=5,
故答案为:5.
三、解答题
19.
解:(1)因为羊的头数太多,不宜采用全面调查方式去调查,应先用省时省力的方式采用抽样调查;
故答案为:抽样调查
(2)由题意可知,总体是300羊的质量;个体是每只羊的质量;样本是所抽取的5只羊的质量;
故答案为:300只羊的质量,每只羊的质量,所抽取的5只羊的质量
②(千克),
(元).
即估计这300只羊能卖106920元.
20.
(1)解:(人),
∴一周内到校运动健身的市民总人数为500人;
(2)羽毛球的人数为人,
健走的百分比为,
补全统计图如下:
(3)根据统计图给出的数据,得出结论:跑步和健走占比是总体的,
所以我认为应加大跑步和健走的项目的投入.
21.
解:(1)这次被调查的学生人数为(人).
(2)C学科人数为200﹣(20+80+40)=60(人),
补全图形如下:
(3)扇形统计图中B学科所占的百分比是,
C学科所占的百分比是,
D学科所占的百分比是.
22.
解:样本容量=,,
如下图所示:
由题意可得,
超过80分的人数比有:,
优秀人数为:人.
答:该校八年级学生中汉字听写能力优秀的约有416人.
23.
解:(1)根据图a可知,分数60-70之间的人数有6人,频率为15%,
所以参加决赛的学生总数为人,
∵80-90分段的频率为25%,
∴80-90分段的频数为人,
故答案为:40.
补充图b如下:
(2)根据(1)问中已求出的80-90分段的频数10即为m,
从表a可知,70-80分段人数为19,
所以,
故答案为:10;47.5%.
(3)由表a可知,80分以上人数有10+5=15人,
所以优秀率=,
故答案为:37.5%.
24.
解:(1)由第一次测评的数学成绩频数分布直方图可知参与总人数为:
(人),
根据两次开展数学拓展活动的人数相同,
,
故答案是:;
(2)①根据第二次测评的数学成绩频数分布表,
可知分及以上人数为:(人),
优秀率为:,
该校名七年级学生数学成绩优秀的人数为:(人);
②根据第一次测评的数学成绩频数分布直方图,
可知分及以上人数为:(人),
优秀率为:,
由(2)①得第二次测评的数学成绩优秀率为:,
,
开展数学拓展活动对学生的学习质量有提升作用.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
