函数的奇偶性
图片预览






文档简介
课件19张PPT。函数的奇偶性
云师大五华实验中学 杨春创设情景:观察图片这些图形有什么共同点?做一做已知函数 f(x) =x2,
求f(-3), f(3), f(-2), f(2), f(-1) ,f(1), f(-a), f(-a)的值 解:f(-3)=(-3)2 =9 , f(3)=32=9可以看出,当自变量x取一对相反数时,相应的两
个函数值相同,即f(-x)=f(x)。f(-2)=(-2)2=4 , f(2)=22=4f(-1)=(-1)2=1 , f(1)=12=1f(-a)=(-a)2=a2 , f(a)=a2如果对于f(x)定义域内的任意一个x,
- X也在定义域内,如果都有f(-x)=f(x),
那么函数f(x)就叫偶函数. 偶函数定义:
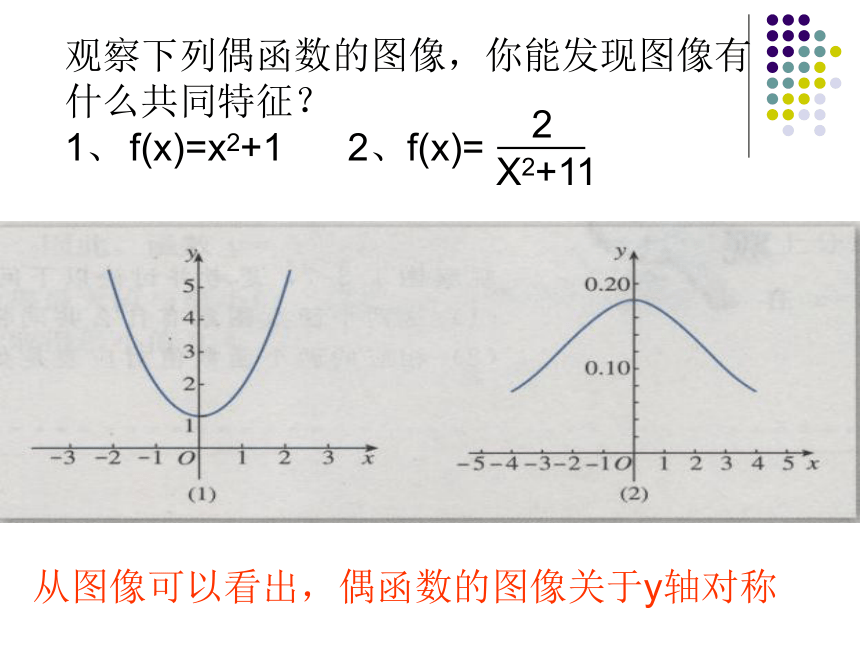
观察下列偶函数的图像,你能发现图像有
什么共同特征?
1、 f(x)=x2+1 2、f(x)=从图像可以看出,偶函数的图像关于y轴对称做一做已知函数f(x) =
求f(-3), f(3), f(-2), f(2), f(-1) ,f(1), f(-a), f(-a)的值
可以看出,当自变量x取一对相反数时,相应的两
个函数值也互为相反数,即f(-x)=-f(x)。如果对于f(x)定义域内的任意一个x,
- X也在定义域内,如果都有f(-x)=-f(x),
那么函数f(x)就叫奇函数. 奇函数定义:
观察下列奇函数的图像,你能发现图像什么共同特征?
1、 f(x)=x 2、f(x)=
f(x)=x2f(x)=|x|从图像可以看出,奇函数的图像关于坐标原点
中心对称想一想:如何判断一个函数是偶函数还是
奇函数?你有些什么办法?判断下列函数是奇函数还是偶函数?为什么?
f(x)=x2 (2) f(x)=x3
议一议:
我们知道f(x)=x2是偶函数,试判断
(1)f(x)=x2( 0(2)f(x)=x2(-2(3)f(x)=x2(-4(4) f(x)=x2 (x≠0) 是偶函数吗?因此,判定一个函数的奇偶性时,要特别
关注函数的定义域!例、判断下列函数的奇偶性(1) f(x)=x4 (2) f(x)=x5
想一想:2、函数f(x)=0是奇函数还是偶函数 ?既是偶函数也是奇函数1、函数 f(x)=x+1是奇函数还是偶函数?既不是奇函数也不是偶函数f(x)=x+1f(x)=0函数奇函数偶函数既是奇函数又是偶函数非奇非偶的函数想一想:已知函数f(x)是偶函数,在(-?,0]上的图象如图,你能试作出[0,?)内的图象吗?想一想:已知函数f(x)是奇函数,在(-?,0]上的图象如图,你能试作出 [0,?)内的图象。思考(1)判断函数f(x)=x3+x的奇偶性
(2)如图是函数f(x)=x3+x图像的一部份,你能画出它在y 轴左边的图像吗?小结:2、奇偶函数的性质:
奇函数的图象关于原点中心对称。
偶函数的图象关于y轴对称。 如果一个函数的图象关于原点对称,那么这个函数是奇函数。
如果一个函数的图象关于y轴对称, 那么这个函数是偶函数。1、奇偶函数的定义:
云师大五华实验中学 杨春创设情景:观察图片这些图形有什么共同点?做一做已知函数 f(x) =x2,
求f(-3), f(3), f(-2), f(2), f(-1) ,f(1), f(-a), f(-a)的值 解:f(-3)=(-3)2 =9 , f(3)=32=9可以看出,当自变量x取一对相反数时,相应的两
个函数值相同,即f(-x)=f(x)。f(-2)=(-2)2=4 , f(2)=22=4f(-1)=(-1)2=1 , f(1)=12=1f(-a)=(-a)2=a2 , f(a)=a2如果对于f(x)定义域内的任意一个x,
- X也在定义域内,如果都有f(-x)=f(x),
那么函数f(x)就叫偶函数. 偶函数定义:
观察下列偶函数的图像,你能发现图像有
什么共同特征?
1、 f(x)=x2+1 2、f(x)=从图像可以看出,偶函数的图像关于y轴对称做一做已知函数f(x) =
求f(-3), f(3), f(-2), f(2), f(-1) ,f(1), f(-a), f(-a)的值
可以看出,当自变量x取一对相反数时,相应的两
个函数值也互为相反数,即f(-x)=-f(x)。如果对于f(x)定义域内的任意一个x,
- X也在定义域内,如果都有f(-x)=-f(x),
那么函数f(x)就叫奇函数. 奇函数定义:
观察下列奇函数的图像,你能发现图像什么共同特征?
1、 f(x)=x 2、f(x)=
f(x)=x2f(x)=|x|从图像可以看出,奇函数的图像关于坐标原点
中心对称想一想:如何判断一个函数是偶函数还是
奇函数?你有些什么办法?判断下列函数是奇函数还是偶函数?为什么?
f(x)=x2 (2) f(x)=x3
议一议:
我们知道f(x)=x2是偶函数,试判断
(1)f(x)=x2( 0
关注函数的定义域!例、判断下列函数的奇偶性(1) f(x)=x4 (2) f(x)=x5
想一想:2、函数f(x)=0是奇函数还是偶函数 ?既是偶函数也是奇函数1、函数 f(x)=x+1是奇函数还是偶函数?既不是奇函数也不是偶函数f(x)=x+1f(x)=0函数奇函数偶函数既是奇函数又是偶函数非奇非偶的函数想一想:已知函数f(x)是偶函数,在(-?,0]上的图象如图,你能试作出[0,?)内的图象吗?想一想:已知函数f(x)是奇函数,在(-?,0]上的图象如图,你能试作出 [0,?)内的图象。思考(1)判断函数f(x)=x3+x的奇偶性
(2)如图是函数f(x)=x3+x图像的一部份,你能画出它在y 轴左边的图像吗?小结:2、奇偶函数的性质:
奇函数的图象关于原点中心对称。
偶函数的图象关于y轴对称。 如果一个函数的图象关于原点对称,那么这个函数是奇函数。
如果一个函数的图象关于y轴对称, 那么这个函数是偶函数。1、奇偶函数的定义:
