直线与圆位置关系(第二课时)
文档属性
| 名称 | 直线与圆位置关系(第二课时) |

|
|
| 格式 | rar | ||
| 文件大小 | 141.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-09-30 00:00:00 | ||
图片预览



文档简介
课件23张PPT。24.2.2 直线和圆的位置关系(2)
-----切线的判定定理和性质定理
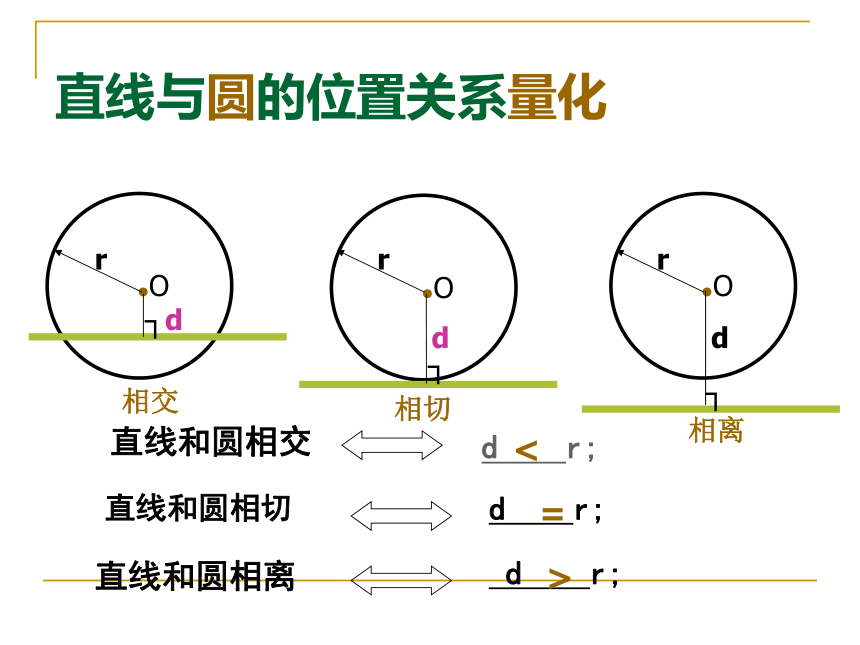
直线和圆相切d r;d r; 直线和圆相交直线和圆相离 d r;直线与圆的位置关系量化<=>3、观察与发现
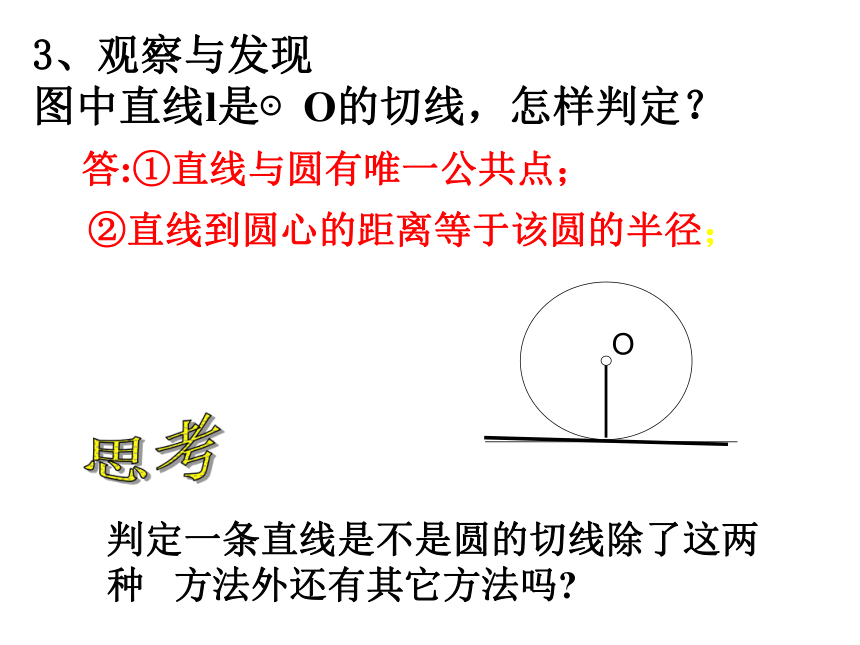
图中直线l是⊙O的切线,怎样判定?答:①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
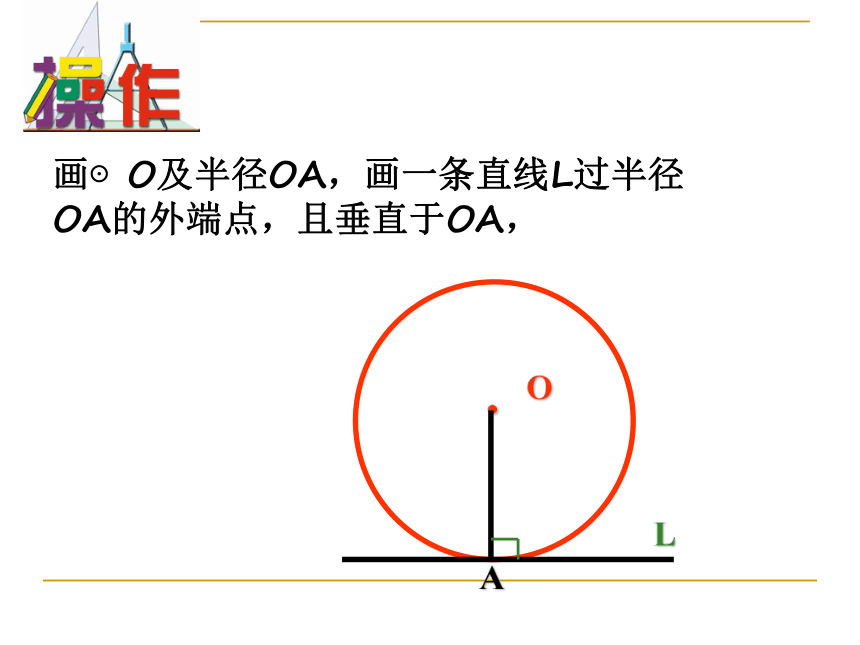
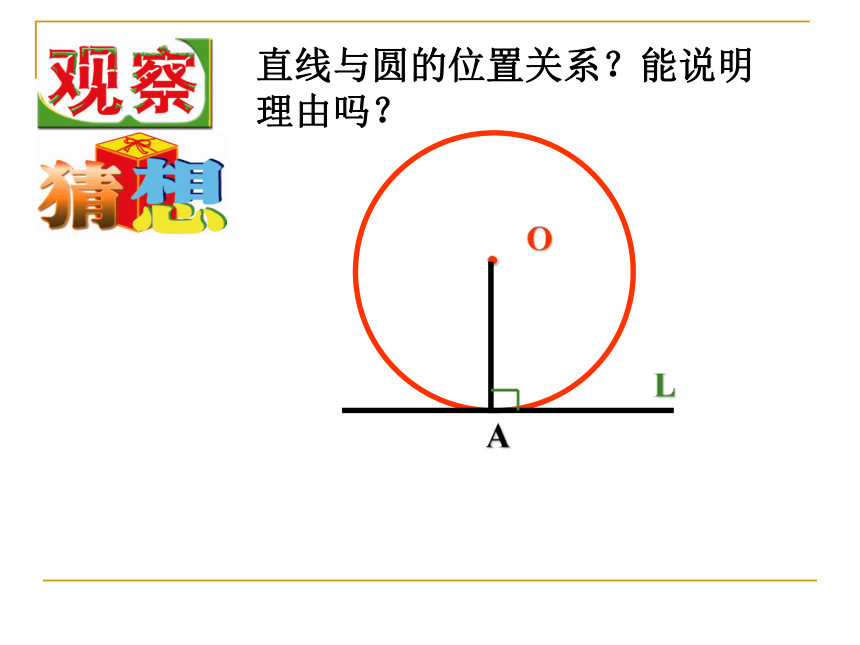
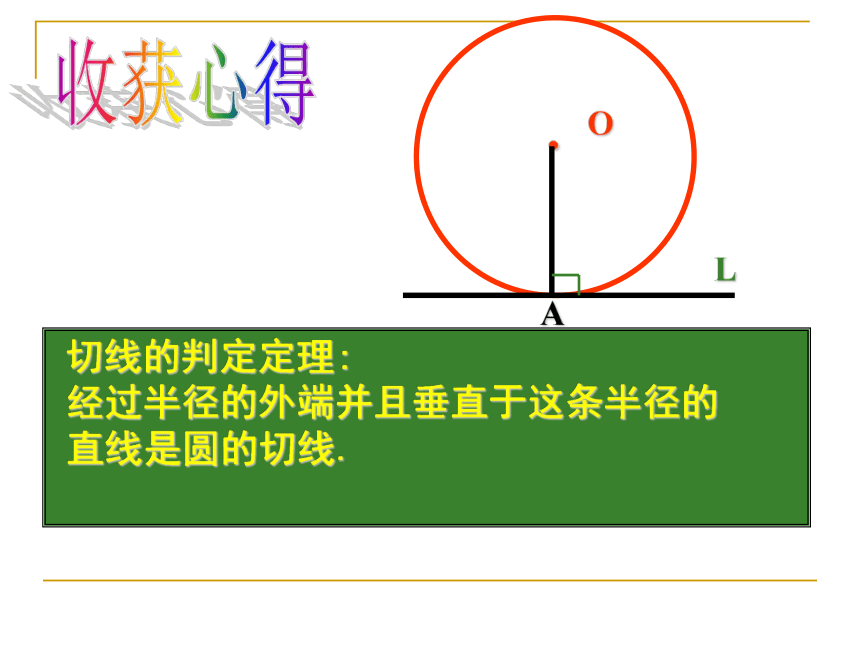
思考判定一条直线是不是圆的切线除了这两种 方法外还有其它方法吗?.OAL画⊙O及半径OA,画一条直线L过半径OA的外端点,且垂直于OA,直线与圆的位置关系?能说明理由吗?.OAL.OAL切线的判定定理:
经过半径的外端并且垂直于这条半径的
直线是圆的切线.收获心得(二)切线的判定定理:
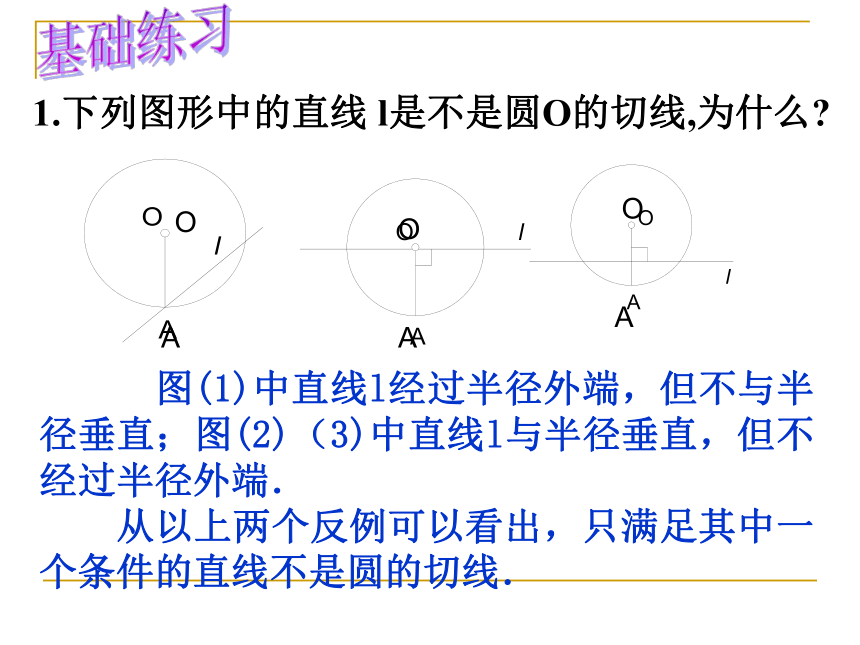
1、切线的判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.2、对定理的理解:切线需满足两条: ①经过半径外端.②垂直于这条半径. 注意:定理中的两个条件缺一不可. 图(1)中直线l经过半径外端,但不与半径垂直;图(2)(3)中直线l与半径垂直,但不经过半径外端.
从以上两个反例可以看出,只满足其中一个条件的直线不是圆的切线.
1.下列图形中的直线 l是不是圆O的切线,为什么?基础练习AAOAOO2.判断下列命题是否正确.
(1)经过半径外端的直线是圆的切线.( )
(2)垂直于半径的直线是圆的切线.( )
(3)过直径的外端并且垂直于这条直径的直线是圆的切线.( )
(4)和圆有一个公共点的直线是圆的切线.( )
(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切.( )
错错对错对(三)切线的判定方法切线的判定方法有三种:①直线与圆有唯一公共点;②直线到圆心的距离等于该圆的半径;③切线的判定定理.1.直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.①过半径外端
②垂直于这条半径。辅助线:
有点连圆心,证垂直例2.如图,线段AB经过圆心O,交⊙O于点A,C,∠BAD=∠B=30°,边BD交圆于点D。
求证:BD是⊙O的切线证明:连结OD∵ OA=OD , ∴ OD⊥BD又∵直线BD 经过⊙O上的D点∴直线BD是⊙O的切线∴∠ODA=∠A=300ABCD∴∠BDO=90°例3、如图⊙O的半径为8,弦AB= ,以O为圆心,4为半径作小圆,求证:AB与小圆O相切.证明:
过O作OC⊥AB于C,连结OA证明直线和圆相切的类型二:
无交点,作垂直,证等于半径.2.如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,判断⊙D与OA的位置关系,
并证明你的结论。辅助线:
无点做垂线,证相等.OAL已知直线L 是⊙O的切线,切点为A,连接0A,你发现了什么?切线的性质定理:圆的切线垂直于过切点的半径。收获心得.OAL①过半径外端
②垂直于这条半径。切线①圆的切线
②过切点的半径。切线垂直于半径判定定理:性质定理:例:在Rt△ABC的斜边上,以AD为直径的⊙O和BC相切于点F, ⊙O和AC交于E
求证:弧EF=弧FDDCOFBA.E1如图, ⊙O切PB于点B,PB=4,PA=2,则
⊙O的半径多少?2 如图:PA,PC分别切圆O于点A,C两点,B为圆O上与A,C不重合的点,若∠P=50°,则∠ABC=___自我检验 如图(a)AB为⊙O的直径,△ABC
内接于⊙O,且∠CAE=∠B
1、试说明AE与⊙O相切于点A。
2、如图(b),若AB是⊙O的非直径的弦,且∠CAE=∠B,AE与⊙O还相切于点A吗? 自我提高切线的判定方法有三种:①直线与圆有唯一公共点;②直线到圆心的距离等于该圆的半径;③切线的判定定理.反思与小结性质定理:圆的切线垂直于过切点的半径。求证:经过直径两端点的切线互相平行练习3 已知:如图,AB 是⊙O的直径,AC、BD是⊙O的切线.
证明:如图,AB 是⊙O的直径AC、BD是⊙O的切线AB⊥ACAB⊥BDAC∥BD求证: AC∥BD⊙O 是△APC的外接圆,BD是
⊙O的切线,切点为A,∠C=500
则∠PAD=______DCOPBA.
-----切线的判定定理和性质定理
直线和圆相切d r;d r; 直线和圆相交直线和圆相离 d r;直线与圆的位置关系量化<=>3、观察与发现
图中直线l是⊙O的切线,怎样判定?答:①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
思考判定一条直线是不是圆的切线除了这两种 方法外还有其它方法吗?.OAL画⊙O及半径OA,画一条直线L过半径OA的外端点,且垂直于OA,直线与圆的位置关系?能说明理由吗?.OAL.OAL切线的判定定理:
经过半径的外端并且垂直于这条半径的
直线是圆的切线.收获心得(二)切线的判定定理:
1、切线的判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.2、对定理的理解:切线需满足两条: ①经过半径外端.②垂直于这条半径. 注意:定理中的两个条件缺一不可. 图(1)中直线l经过半径外端,但不与半径垂直;图(2)(3)中直线l与半径垂直,但不经过半径外端.
从以上两个反例可以看出,只满足其中一个条件的直线不是圆的切线.
1.下列图形中的直线 l是不是圆O的切线,为什么?基础练习AAOAOO2.判断下列命题是否正确.
(1)经过半径外端的直线是圆的切线.( )
(2)垂直于半径的直线是圆的切线.( )
(3)过直径的外端并且垂直于这条直径的直线是圆的切线.( )
(4)和圆有一个公共点的直线是圆的切线.( )
(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切.( )
错错对错对(三)切线的判定方法切线的判定方法有三种:①直线与圆有唯一公共点;②直线到圆心的距离等于该圆的半径;③切线的判定定理.1.直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.①过半径外端
②垂直于这条半径。辅助线:
有点连圆心,证垂直例2.如图,线段AB经过圆心O,交⊙O于点A,C,∠BAD=∠B=30°,边BD交圆于点D。
求证:BD是⊙O的切线证明:连结OD∵ OA=OD , ∴ OD⊥BD又∵直线BD 经过⊙O上的D点∴直线BD是⊙O的切线∴∠ODA=∠A=300ABCD∴∠BDO=90°例3、如图⊙O的半径为8,弦AB= ,以O为圆心,4为半径作小圆,求证:AB与小圆O相切.证明:
过O作OC⊥AB于C,连结OA证明直线和圆相切的类型二:
无交点,作垂直,证等于半径.2.如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,判断⊙D与OA的位置关系,
并证明你的结论。辅助线:
无点做垂线,证相等.OAL已知直线L 是⊙O的切线,切点为A,连接0A,你发现了什么?切线的性质定理:圆的切线垂直于过切点的半径。收获心得.OAL①过半径外端
②垂直于这条半径。切线①圆的切线
②过切点的半径。切线垂直于半径判定定理:性质定理:例:在Rt△ABC的斜边上,以AD为直径的⊙O和BC相切于点F, ⊙O和AC交于E
求证:弧EF=弧FDDCOFBA.E1如图, ⊙O切PB于点B,PB=4,PA=2,则
⊙O的半径多少?2 如图:PA,PC分别切圆O于点A,C两点,B为圆O上与A,C不重合的点,若∠P=50°,则∠ABC=___自我检验 如图(a)AB为⊙O的直径,△ABC
内接于⊙O,且∠CAE=∠B
1、试说明AE与⊙O相切于点A。
2、如图(b),若AB是⊙O的非直径的弦,且∠CAE=∠B,AE与⊙O还相切于点A吗? 自我提高切线的判定方法有三种:①直线与圆有唯一公共点;②直线到圆心的距离等于该圆的半径;③切线的判定定理.反思与小结性质定理:圆的切线垂直于过切点的半径。求证:经过直径两端点的切线互相平行练习3 已知:如图,AB 是⊙O的直径,AC、BD是⊙O的切线.
证明:如图,AB 是⊙O的直径AC、BD是⊙O的切线AB⊥ACAB⊥BDAC∥BD求证: AC∥BD⊙O 是△APC的外接圆,BD是
⊙O的切线,切点为A,∠C=500
则∠PAD=______DCOPBA.
同课章节目录
