由数列递推公式求通项公式的八种方法
文档属性
| 名称 | 由数列递推公式求通项公式的八种方法 |

|
|
| 格式 | rar | ||
| 文件大小 | 101.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-09-28 00:00:00 | ||
图片预览

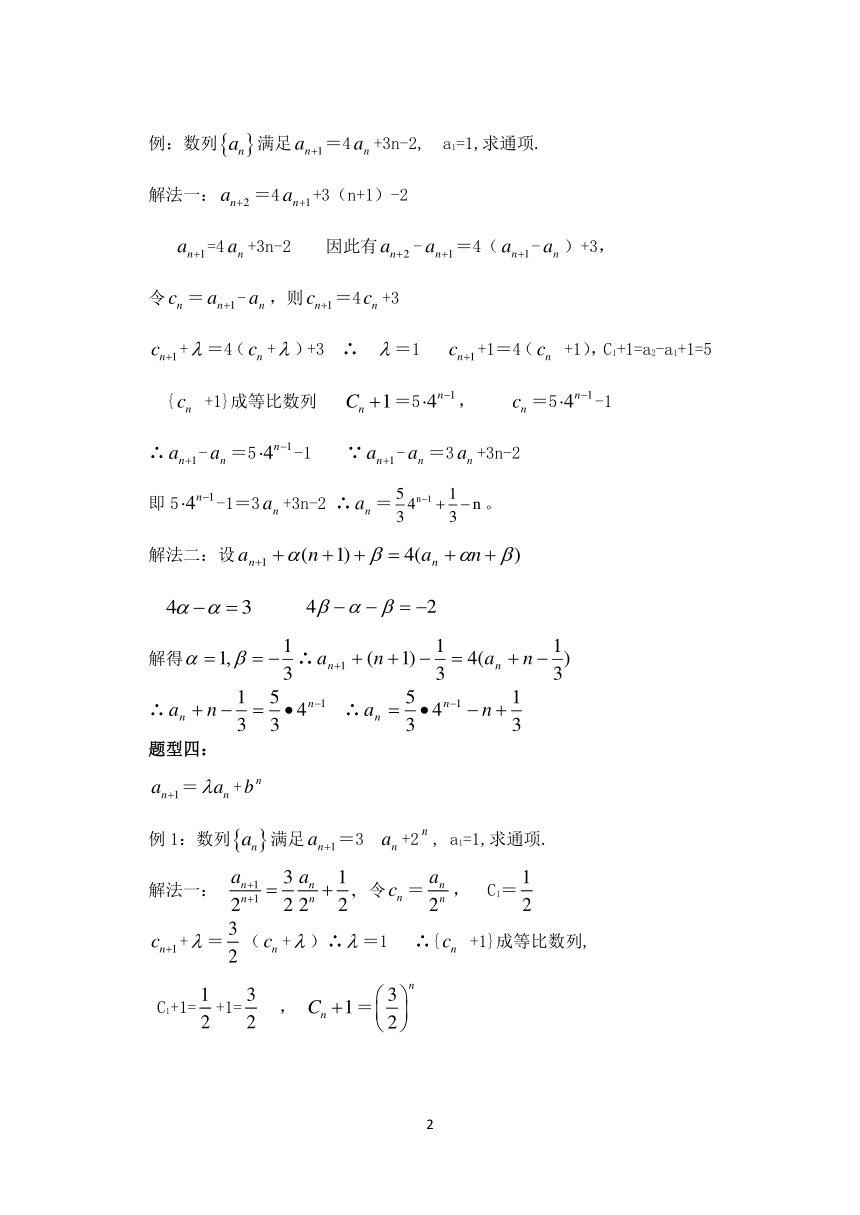

文档简介
数列专题:递推公式求通项公式
题型一:
⑴.(差后等差数列)
例1. 数列中,,,求
⑵ (差后等比数列)
例2. 已知数列{an}中,a1=1,且an=an-1+3n-1,求{an}的通项公式.
题型二:
=+ (相邻两项满足线性关系)
例.数列满足=2+3, a1=1求通项.
解:(+)=2(+) ∴=3 ∴ +3=2(+3) 即{+3}成G.P 公比q=2首项a1+3=4 ∴+3=42∴=-3
练习:在数列{an}中,a1=2,且an+1=,求{an}的通项公式.
解:an+12=an2+
∴an+12-1=(an2-1)
∴{an+12-1}是以3为首项,公比为的等差数列.
∴an+12-1=3×,即an=
题型三:
=+
例:数列满足=4+3n-2, a1=1,求通项.
解法一:=4+3(n+1)-2
=4+3n-2 因此有-=4(-)+3,
令=-,则=4+3
+=4(+)+3 ∴ =1 +1=4( +1),C1+1=a2-a1+1=5 { +1}成等比数列 =5, =5-1
∴-=5-1 ∵-=3+3n-2
即5-1=3+3n-2 ∴=。
解法二:设
解得∴
∴∴
题型四:
=+
例1:数列满足=3+2, a1=1,求通项.
解法一: 令=, C1=
+=(+)∴=1 ∴{ +1}成等比数列,
C1+1=+1= , =
∴=-1 == -
解法二:设
∴
∴∴
例2:(05江西文)数列的前n项和满足-=3(),且=1, =-,求通项公式.
=+==3
+=3,令=-2=-6
+=2(+), 2-=-6=-6-6=2(-6)∵=-2=-2
∴-6=-8, -6=-8 =-∴=6-=(6-)=3-4
即= .
题型五:=f(n)
由=f(n-1)f(n-2)┈f(1)a1 即“累积法”求
例:数列满足a1=1,= (n2)求的通项公式.
解:=
=+n ∴ -= n, =n+1,注意n2且a1=1,
∴==n(n-1)┈3 ∴2= (n2) ∴=
题型六:=p+q (p、q均为常数)
=p+q -=(-)∴解出、因此{-}是等比数列
例1:a1=1,a2= =-,求数列{}的通项公式。
解:-=(-)解得:=1、=
-=(-), a2-a1= ∴-= ∴=(-)+(-)+┈+(a2-a1)+a1=++┈++1=3-.
∴=3-
题型七:
连续两项之间不满足线性关系的。
例1.(倒数法)已知数列{an}中,a1=,an+1=,求{an}的通项公式.
解:
∴是以为首项,公差为2的等差数列,
即+2(n-1)=
∴an=
例2:(对数法)数列满足a1=2,2=+,求的通项。
解:=,且2>2>1 ∴>1恒成立。
+1=, -1=成等比数列
q=3,首项lg3, ∴lg= ∴=
例3.(三角代换法)已知数列{an}中,a1=2,an=,求{an}的通项公式.
解:令an-1=tan,则an+1==tan
∴an=tan.
题型八
用求解:数列的前n项和与的隐含关系为,利用这个关系揭示与的关系或与的关系,使数列化归为两个基本的数列求解
例1、为数列的前n项和,且,首项
(1) 若,求证:数列为等比数列
(2)、设,求证:数列为等比数列
(3)、求数列的通项公式及前n项和公式
PAGE
6
题型一:
⑴.(差后等差数列)
例1. 数列中,,,求
⑵ (差后等比数列)
例2. 已知数列{an}中,a1=1,且an=an-1+3n-1,求{an}的通项公式.
题型二:
=+ (相邻两项满足线性关系)
例.数列满足=2+3, a1=1求通项.
解:(+)=2(+) ∴=3 ∴ +3=2(+3) 即{+3}成G.P 公比q=2首项a1+3=4 ∴+3=42∴=-3
练习:在数列{an}中,a1=2,且an+1=,求{an}的通项公式.
解:an+12=an2+
∴an+12-1=(an2-1)
∴{an+12-1}是以3为首项,公比为的等差数列.
∴an+12-1=3×,即an=
题型三:
=+
例:数列满足=4+3n-2, a1=1,求通项.
解法一:=4+3(n+1)-2
=4+3n-2 因此有-=4(-)+3,
令=-,则=4+3
+=4(+)+3 ∴ =1 +1=4( +1),C1+1=a2-a1+1=5 { +1}成等比数列 =5, =5-1
∴-=5-1 ∵-=3+3n-2
即5-1=3+3n-2 ∴=。
解法二:设
解得∴
∴∴
题型四:
=+
例1:数列满足=3+2, a1=1,求通项.
解法一: 令=, C1=
+=(+)∴=1 ∴{ +1}成等比数列,
C1+1=+1= , =
∴=-1 == -
解法二:设
∴
∴∴
例2:(05江西文)数列的前n项和满足-=3(),且=1, =-,求通项公式.
=+==3
+=3,令=-2=-6
+=2(+), 2-=-6=-6-6=2(-6)∵=-2=-2
∴-6=-8, -6=-8 =-∴=6-=(6-)=3-4
即= .
题型五:=f(n)
由=f(n-1)f(n-2)┈f(1)a1 即“累积法”求
例:数列满足a1=1,= (n2)求的通项公式.
解:=
=+n ∴ -= n, =n+1,注意n2且a1=1,
∴==n(n-1)┈3 ∴2= (n2) ∴=
题型六:=p+q (p、q均为常数)
=p+q -=(-)∴解出、因此{-}是等比数列
例1:a1=1,a2= =-,求数列{}的通项公式。
解:-=(-)解得:=1、=
-=(-), a2-a1= ∴-= ∴=(-)+(-)+┈+(a2-a1)+a1=++┈++1=3-.
∴=3-
题型七:
连续两项之间不满足线性关系的。
例1.(倒数法)已知数列{an}中,a1=,an+1=,求{an}的通项公式.
解:
∴是以为首项,公差为2的等差数列,
即+2(n-1)=
∴an=
例2:(对数法)数列满足a1=2,2=+,求的通项。
解:=,且2>2>1 ∴>1恒成立。
+1=, -1=成等比数列
q=3,首项lg3, ∴lg= ∴=
例3.(三角代换法)已知数列{an}中,a1=2,an=,求{an}的通项公式.
解:令an-1=tan,则an+1==tan
∴an=tan.
题型八
用求解:数列的前n项和与的隐含关系为,利用这个关系揭示与的关系或与的关系,使数列化归为两个基本的数列求解
例1、为数列的前n项和,且,首项
(1) 若,求证:数列为等比数列
(2)、设,求证:数列为等比数列
(3)、求数列的通项公式及前n项和公式
PAGE
6
