3.2 空间向量基本定理 课件(共33张PPT) 2023-2024学年高二数学同步课堂(沪教版2020选择性必修第一册)
文档属性
| 名称 | 3.2 空间向量基本定理 课件(共33张PPT) 2023-2024学年高二数学同步课堂(沪教版2020选择性必修第一册) |

|
|
| 格式 | pptx | ||
| 文件大小 | 47.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-03 20:10:17 | ||
图片预览







文档简介
(共33张PPT)
3.2空间向量基本定理
第3章 空间向量及其应用
教师
xxx
沪教版(2020)选择性必修第一册
向量共面的充要条件
空间向量基本定理的应用
空间向量的基本定理
01
03
02
CONTANTS
目 录
向量共面的充要条件
01
向量共面的充要条件(平面向量基本定理):
如果 , 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量,有且只有一对实数 ,μ,使
= + μ .
若 , 不共线,我们把{, }叫做表示这一平面内所有向量的一个基底.
例题1.如图3- 2- 2,在长方体ABCD-A1B1C1D1 中,点E是棱AA1 的中点,点O是面对角线BC1 与B1C的交点,试判断向量 是否共面.
例题2.利用向量证明:如果一条直线垂直于一个平面内的两条相交直线,那么这条直线垂直于这个平面(即垂直于这个平面中的任何直线).
空间向量的基本定理
02
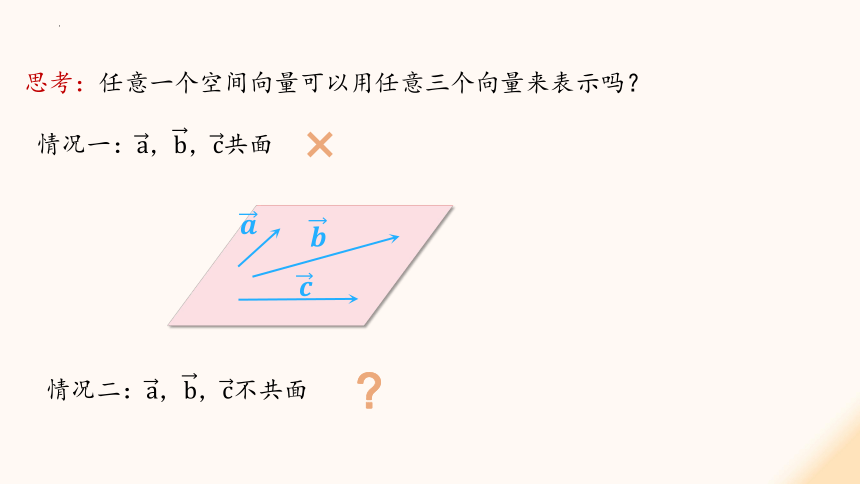
思考:任意一个空间向量可以用任意三个向量来表示吗?
情况一:共面
情况二:不共面
?
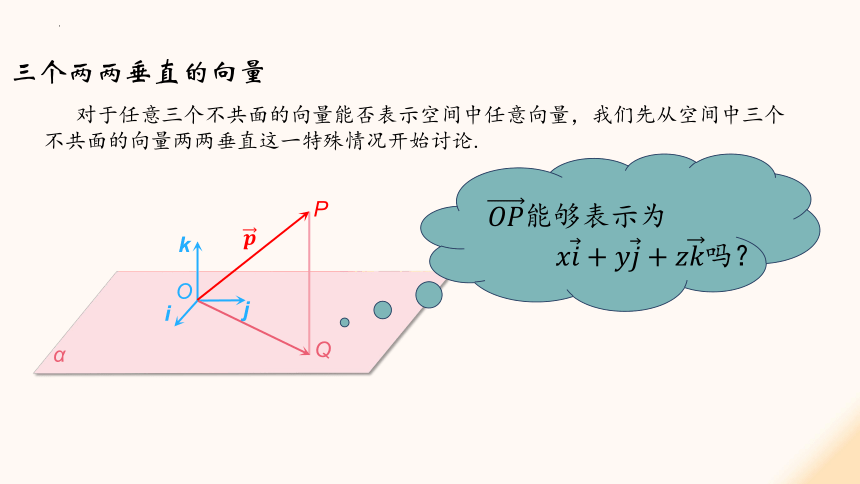
对于任意三个不共面的向量能否表示空间中任意向量,我们先从空间中三个不共面的向量两两垂直这一特殊情况开始讨论.
三个两两垂直的向量
i
j
k
P
Q
α
O
表示为
吗?
i
j
k
yj
zk
xi
P
xi
i
j
k
P
yj
zk
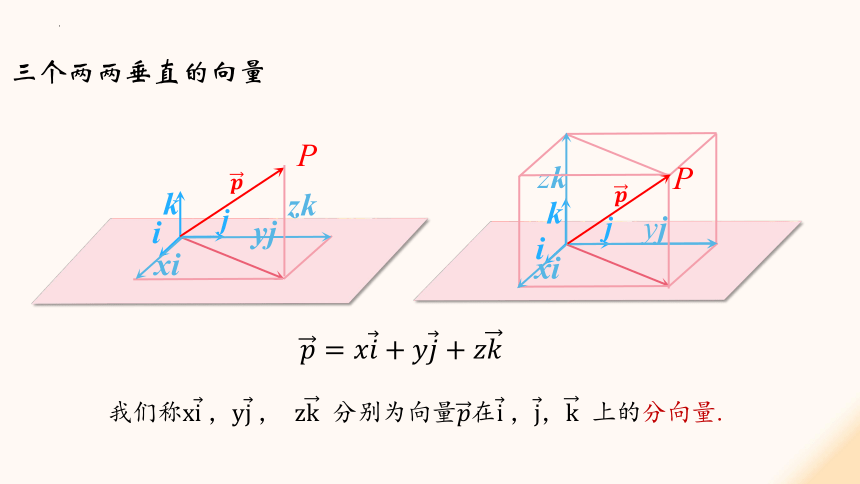
三个两两垂直的向量
我们称,, 分别为向量在 上的分向量.
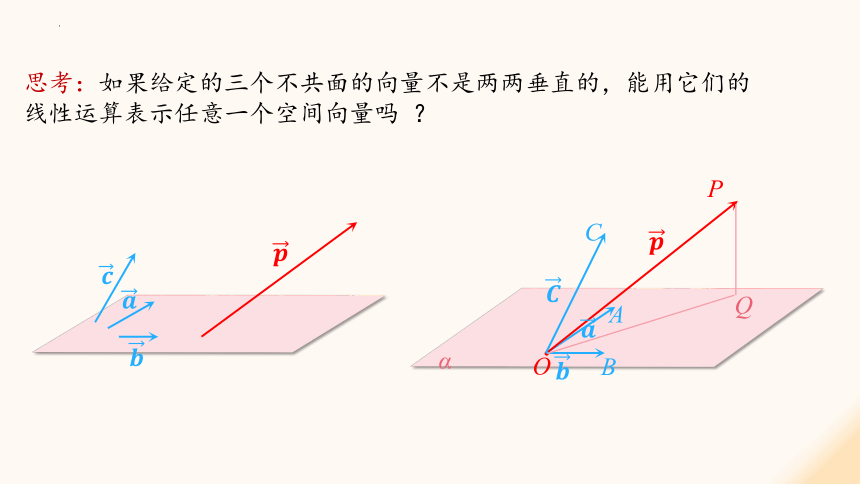
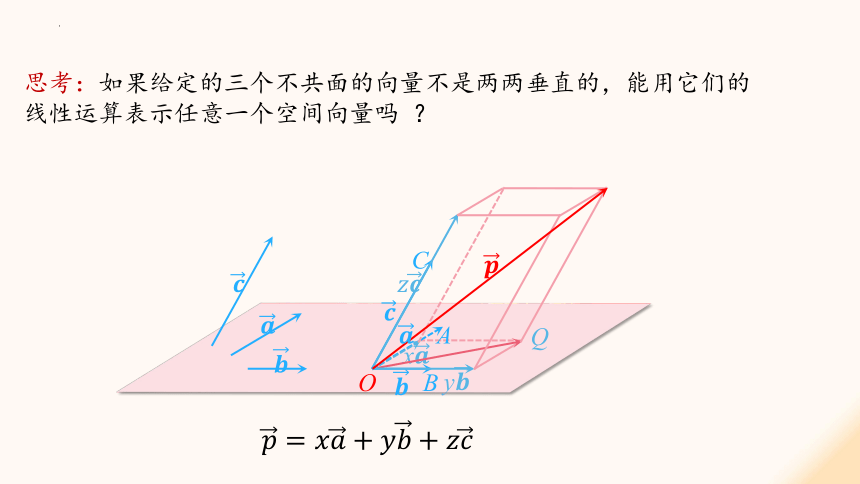
思考:如果给定的三个不共面的向量不是两两垂直的,能用它们的线性运算表示任意一个空间向量吗 ?
α
O
P
B
C
A
Q
x
O
Q
y
B
C
A
思考:如果给定的三个不共面的向量不是两两垂直的,能用它们的线性运算表示任意一个空间向量吗 ?
如果 , 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量,有且只有一对实数 ,μ,使
= + μ .
若 , 不共线,我们把{, }叫做表示这一平面内所有向量的一个基底.
你能类比平面向量基本定理,写出空间向量基本定理吗?
空间向量基本定理
如果三个向量不共面,那么对任意一个空间向量,存在唯一的有序实数组,使得
.
若三个向量不共面,我们把叫做空间向量的一个基底,都叫做基向量.空间任意三个不共面的向量都可以构成空间的一个基底.
空间的基底有无数个
特别地,我们常研究基向量两两垂直的情况
特别地,如果空间的一个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做单位正交基底,常用表示.
由空间向量基本定理知,对空间中的任意向量,均可以分解为三个向量,, ,使
.
像这样,把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.
则2e1-e2+3e3=p(e1+2e2-e3)+q(-3e1+e2+2e3)+z(e1+e2-e3)
=(p-3q+z)e1+(2p+q+z)e2+(-p+2q-z)e3.
∵{e1,e2,e3}为空间的一个基底,
反思感悟 用基底表示空间向量的解题策略
1.空间中,任一向量都可以用一个基底表示,且只要基底确定,则表示形式是唯一的.
2.用基底表示空间向量时,一般要结合图形,运用向量加法、减法的平行四边形法则、三角形法则,以及数乘向量的运算法则,逐步向基向量过渡,直至全部用基向量表示.
3.在空间几何体中选择基底时,通常选取公共起点最集中的向量或关系最明确的向量作为基底,例如,在正方体、长方体、平行六面体、四面体中,一般选用从同一顶点出发的三条棱所对应的向量作为基底.
空间向量基本定理的应用
03
1.如图,在正方体ABCD A1B1C1D1中,E,F分别是BB1,D1B1的中点,求证:EF⊥AB1.
2如图,在直三棱柱ABC-A’B’C’中,AC=BC=AA’,,D,E 分别为 AB ,BB’的中点
(1)求证:CE;
(2)求异面直线 CE 与 A’C所成角的余弦值.
解:设 ,,,
根据题意得 ,且 ∴ ,
.∴ =,∴ ,即CE .
2如图,在直三棱柱ABC-A’B’C’中,AC=BC=AA’,,D,E 分别为 AB ,BB’的中点
(1)求证:CE;
(2)求异面直线 CE 与 A’C所成角的余弦值.
(2)∵ ,∴,,
∵=,∴cos.
∴异面直线CE与A’C所成角的余弦值为.
利用空间向量基本定理解决几何问题的步骤:
(1)把几何问题转化为向量问题.
(2)选择空间的某个基底表示未知向量.
(3)证明垂直问题时,需结合数量积公式和运算律证明数量积为0;
求异面直线所成角,利用夹角公式cos θ=|cos〈a,b〉|.
(4)将向量问题回归到几何问题.
方法总结
3.如图,三棱柱ABC A1B1C1中,M,N分别是A1B,B1C1上的点,且BM=2A1M,C1N=2B1N.设 =a,=b,=c.
(1)试用a,b,c表示向量 ;
(2)若∠BAC=90°,∠BAA1=∠CAA1=60°,AB=AC=AA1=1,求MN的长.
解:(1)=++=++=(c-a)+a+(b-a)=a+b+c.
3.如图,三棱柱ABC A1B1C1中,M,N分别是A1B,B1C1上的点,且BM=2A1M,C1N=2B1N.设 =a,=b,=c.
(1)试用a,b,c表示向量 ;
(2)若∠BAC=90°,∠BAA1=∠CAA1=60°,AB=AC=AA1=1,求MN的长.
(2)∵(a+b+c)2=a2+b2+c2+2a·b+2b·c+2a·c=1+1+1+0+2×1×1×+2×1×1×=5,
∴|a+b+c|=, ∴||=|a+b+c|=,即MN= .
1.已知空间的一个基底{a,b,c},向量m=a-b+c,n=xa+yb+c,若m与n共线,则x+y等于( )
A.2 B.-2
C.1 D.0
解析:因为m与n共线,所以存在实数λ,使得n=λm,即xa+yb+c=λ(a-b+c).
答案:D
课堂练习
答案:D
3.已知{e1,e2,e3}是空间的一个基底,若λe1+μe2+ve3=0,则λ2+μ2+v2= .
解析:∵{e1,e2,e3}是空间的一个基底,
∴e1,e2,e3为不共面向量.又λe1+μe2+ve3=0,∴λ=μ=v=0.
∴λ2+μ2+v2=0.
答案:0
感谢观看
3.2空间向量基本定理
第3章 空间向量及其应用
教师
xxx
沪教版(2020)选择性必修第一册
向量共面的充要条件
空间向量基本定理的应用
空间向量的基本定理
01
03
02
CONTANTS
目 录
向量共面的充要条件
01
向量共面的充要条件(平面向量基本定理):
如果 , 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量,有且只有一对实数 ,μ,使
= + μ .
若 , 不共线,我们把{, }叫做表示这一平面内所有向量的一个基底.
例题1.如图3- 2- 2,在长方体ABCD-A1B1C1D1 中,点E是棱AA1 的中点,点O是面对角线BC1 与B1C的交点,试判断向量 是否共面.
例题2.利用向量证明:如果一条直线垂直于一个平面内的两条相交直线,那么这条直线垂直于这个平面(即垂直于这个平面中的任何直线).
空间向量的基本定理
02
思考:任意一个空间向量可以用任意三个向量来表示吗?
情况一:共面
情况二:不共面
?
对于任意三个不共面的向量能否表示空间中任意向量,我们先从空间中三个不共面的向量两两垂直这一特殊情况开始讨论.
三个两两垂直的向量
i
j
k
P
Q
α
O
表示为
吗?
i
j
k
yj
zk
xi
P
xi
i
j
k
P
yj
zk
三个两两垂直的向量
我们称,, 分别为向量在 上的分向量.
思考:如果给定的三个不共面的向量不是两两垂直的,能用它们的线性运算表示任意一个空间向量吗 ?
α
O
P
B
C
A
Q
x
O
Q
y
B
C
A
思考:如果给定的三个不共面的向量不是两两垂直的,能用它们的线性运算表示任意一个空间向量吗 ?
如果 , 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量,有且只有一对实数 ,μ,使
= + μ .
若 , 不共线,我们把{, }叫做表示这一平面内所有向量的一个基底.
你能类比平面向量基本定理,写出空间向量基本定理吗?
空间向量基本定理
如果三个向量不共面,那么对任意一个空间向量,存在唯一的有序实数组,使得
.
若三个向量不共面,我们把叫做空间向量的一个基底,都叫做基向量.空间任意三个不共面的向量都可以构成空间的一个基底.
空间的基底有无数个
特别地,我们常研究基向量两两垂直的情况
特别地,如果空间的一个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做单位正交基底,常用表示.
由空间向量基本定理知,对空间中的任意向量,均可以分解为三个向量,, ,使
.
像这样,把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.
则2e1-e2+3e3=p(e1+2e2-e3)+q(-3e1+e2+2e3)+z(e1+e2-e3)
=(p-3q+z)e1+(2p+q+z)e2+(-p+2q-z)e3.
∵{e1,e2,e3}为空间的一个基底,
反思感悟 用基底表示空间向量的解题策略
1.空间中,任一向量都可以用一个基底表示,且只要基底确定,则表示形式是唯一的.
2.用基底表示空间向量时,一般要结合图形,运用向量加法、减法的平行四边形法则、三角形法则,以及数乘向量的运算法则,逐步向基向量过渡,直至全部用基向量表示.
3.在空间几何体中选择基底时,通常选取公共起点最集中的向量或关系最明确的向量作为基底,例如,在正方体、长方体、平行六面体、四面体中,一般选用从同一顶点出发的三条棱所对应的向量作为基底.
空间向量基本定理的应用
03
1.如图,在正方体ABCD A1B1C1D1中,E,F分别是BB1,D1B1的中点,求证:EF⊥AB1.
2如图,在直三棱柱ABC-A’B’C’中,AC=BC=AA’,,D,E 分别为 AB ,BB’的中点
(1)求证:CE;
(2)求异面直线 CE 与 A’C所成角的余弦值.
解:设 ,,,
根据题意得 ,且 ∴ ,
.∴ =,∴ ,即CE .
2如图,在直三棱柱ABC-A’B’C’中,AC=BC=AA’,,D,E 分别为 AB ,BB’的中点
(1)求证:CE;
(2)求异面直线 CE 与 A’C所成角的余弦值.
(2)∵ ,∴,,
∵=,∴cos.
∴异面直线CE与A’C所成角的余弦值为.
利用空间向量基本定理解决几何问题的步骤:
(1)把几何问题转化为向量问题.
(2)选择空间的某个基底表示未知向量.
(3)证明垂直问题时,需结合数量积公式和运算律证明数量积为0;
求异面直线所成角,利用夹角公式cos θ=|cos〈a,b〉|.
(4)将向量问题回归到几何问题.
方法总结
3.如图,三棱柱ABC A1B1C1中,M,N分别是A1B,B1C1上的点,且BM=2A1M,C1N=2B1N.设 =a,=b,=c.
(1)试用a,b,c表示向量 ;
(2)若∠BAC=90°,∠BAA1=∠CAA1=60°,AB=AC=AA1=1,求MN的长.
解:(1)=++=++=(c-a)+a+(b-a)=a+b+c.
3.如图,三棱柱ABC A1B1C1中,M,N分别是A1B,B1C1上的点,且BM=2A1M,C1N=2B1N.设 =a,=b,=c.
(1)试用a,b,c表示向量 ;
(2)若∠BAC=90°,∠BAA1=∠CAA1=60°,AB=AC=AA1=1,求MN的长.
(2)∵(a+b+c)2=a2+b2+c2+2a·b+2b·c+2a·c=1+1+1+0+2×1×1×+2×1×1×=5,
∴|a+b+c|=, ∴||=|a+b+c|=,即MN= .
1.已知空间的一个基底{a,b,c},向量m=a-b+c,n=xa+yb+c,若m与n共线,则x+y等于( )
A.2 B.-2
C.1 D.0
解析:因为m与n共线,所以存在实数λ,使得n=λm,即xa+yb+c=λ(a-b+c).
答案:D
课堂练习
答案:D
3.已知{e1,e2,e3}是空间的一个基底,若λe1+μe2+ve3=0,则λ2+μ2+v2= .
解析:∵{e1,e2,e3}是空间的一个基底,
∴e1,e2,e3为不共面向量.又λe1+μe2+ve3=0,∴λ=μ=v=0.
∴λ2+μ2+v2=0.
答案:0
感谢观看
同课章节目录
