沪科版数学九年级上册 第22章《相似形》单元检测题(含简单答案)
文档属性
| 名称 | 沪科版数学九年级上册 第22章《相似形》单元检测题(含简单答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 568.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-01 21:23:31 | ||
图片预览



文档简介
第22章《相似形》单元检测题
一、单选题(共10小题,满分40分)
1.如图,在△ABC中,DE∥BC,AD:BD=5:3,BC=16,则DE的长为( )
A.6 B.8 C.10 D.12
2.如图,在平面直角坐标系中,,,将以为位似中心缩小一半,则对应的点的坐标( )
A. B.
C.或 D.或
3.如图,在平面直角坐标系中,已知点,,以原点为位似中心,相似比为,把缩小,则点的对应点的坐标是( )
A. B.
C.或 D.或
4.在平面直角坐标系中,点、点,以原点为位似中心,按的比例把缩小,则点的对应点的坐标为( )
A. B.
C.或 D.或
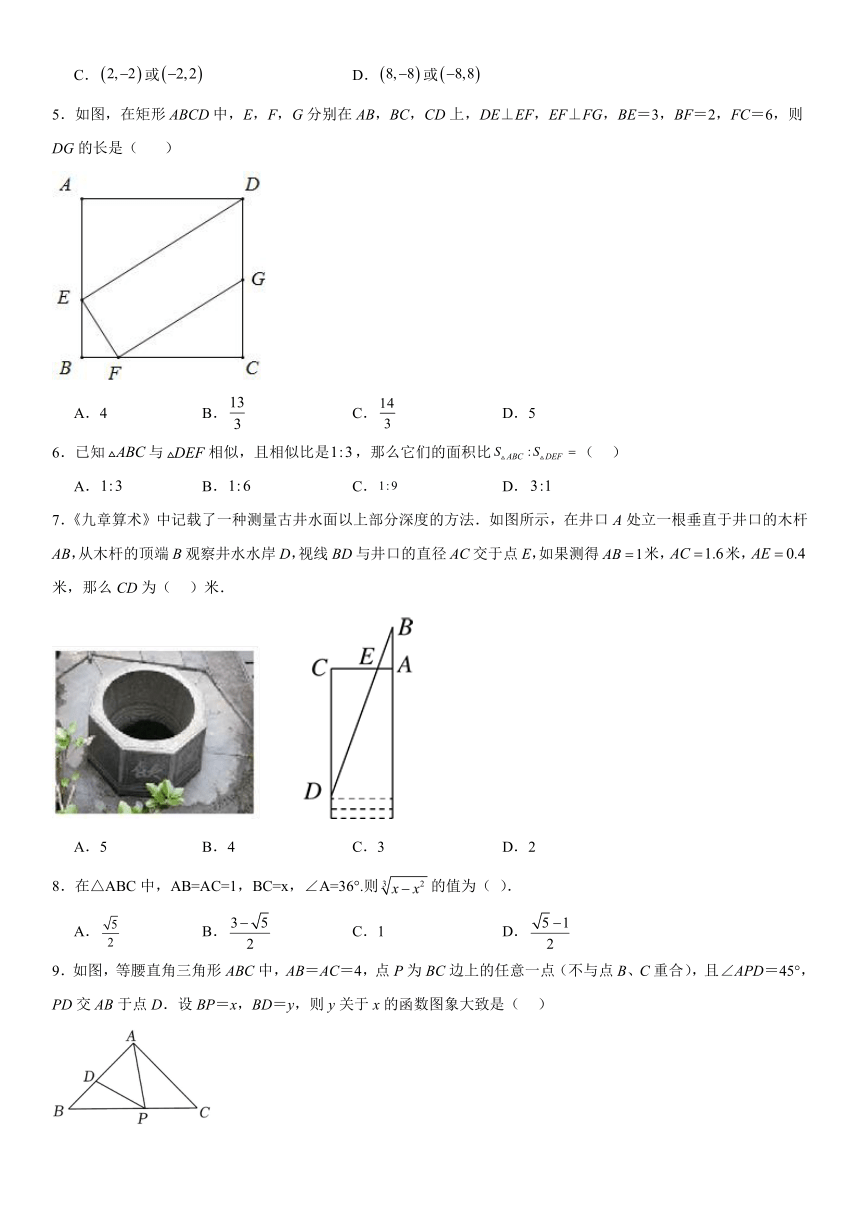
5.如图,在矩形ABCD中,E,F,G分别在AB,BC,CD上,DE⊥EF,EF⊥FG,BE=3,BF=2,FC=6,则DG的长是( )
A.4 B. C. D.5
6.已知与相似,且相似比是,那么它们的面积比( )
A. B. C. D.
7.《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆AB,从木杆的顶端B观察井水水岸D,视线BD与井口的直径AC交于点E,如果测得米,米,米,那么CD为( )米.
A.5 B.4 C.3 D.2
8.在△ABC中,AB=AC=1,BC=x,∠A=36°.则的值为( ).
A. B. C.1 D.
9.如图,等腰直角三角形ABC中,AB=AC=4,点P为BC边上的任意一点(不与点B、C重合),且∠APD=45°,PD交AB于点D.设BP=x,BD=y,则y关于x的函数图象大致是( )
A.B.C. D.
10.如图,在平面直角坐标系中,等边的边经过原点,且顶点,都在的图象上,顶点在的图象上,则的值为( )
A. B. C. D.
二、填空题(共8小题,满分32分)
11.如图,小明同学用自制的直角三角形纸板测量树的高度,他调整自己的位置,设法使斜边保持水平,并且边与点在同一直线上.已知纸板的两条直角边,,测得边离地面的高度,,则树高为
12.如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,则线段AC的长= .
13.如图,线段两个端点的坐标分别为、,以原点为位似中心,将线段放大得到线段,若点的坐标为,则点的坐标为 .
14.如图,D为的AB边上的一点,,若cm,cm,则AD的长为 cm.
15.已知点C是线段AB的黄金分割点(靠近A),AB=2,则BC= .
16.如图,数学活动小组为了测量学校旗杆的高度,使用长为的竹竿作为测量工具.移动竹竿,使竹顶端的影子与旗杆顶端的影子在地面处重合,测得,,则旗杆的高为 .
17.如图,在中,点D、E、F分别在边、、上,,,.如果,那么 .
18.如图所示,已知矩形ABCD的对角线相交于点O,点E、F分别是OD、OC的中点,边AD=4,DC=2,则△OEF的面积为 .
三、解答题(共6小题,每题8分,满分48分)
19.如图,为估算某河的宽度,在河对岸边选定一个目标点,在近岸取点,使得,点在上,并且点在同一条直线上.若测得米,米,米,试求河的宽度.
20.阅读下列材料,回答问题.
任务:测量一棵树的高度,该树的底端可到达,顶部不可到达,如图.
工具:一把皮尺,自制的直角三角形纸板.
测量过程:小明站在点处,调整自己的位置,使得三角尺斜边与地面平行,且边与点在同一直线上.
小亮和小颖用皮尺测量,,,点与点之间的距离.求树高.用含,,,的代数式表示)
21.阅读与思考
下面是某兴趣小组的一次实践活动记录:
兴趣小组札记
2022年×月×日,在数学兴趣小组开展的活动中,小华给每位同学发了一张扇形纸片,并要求大家按照下面的做法画出一个正方形,使得正方形的四个顶点分别落在扇形半径,和上.
小李的做法如下:如图1,先在扇形内画出正方形,使得C,D两点在上,点F在上,连接并延长交于点G,过点G分别作于点J,交于点H,再作于点I.
(1)猜想证明:请问小李画出的四边形是正方形吗?如果是,请给出你的证明;如果不是,请说明理由.
(2)实践操作:如图2,给定锐角三角形,画出一个长宽比为的矩形,使得点D,E位于边上,点F,G分别位于边,上.
22.如图,D、E分别为△ABC的AB、AC边上两点,且AD=5,BD=3,AE=4,CE=6. 求的值.
23.已知:如图
(1)如果,那么吗?为什么?
(2)如果,那么吗?为什么?
24.如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点D从点C出发,以2 cm/s 的速度沿折线C→A→B向点B运动,同时点E从点B出发,以1 cm/s的速度沿BC边向点C运动,设点E运动的时间为t (单位:s)(0<t<8).
(1) 当△BDE 是直角三角形时,求t的值;
(2)若四边形CDEF是以CD、DE为一组邻边的平行四边形,①设它的面积为S,求S关于t的函数关系式;②是否存在某个时刻t,使平行四边形CDEF为菱形 若存在,求出t的值;若不存在,请说明理由.
参考答案:
1.C
2.C
3.D
4.C
5.B
6.C
7.C
8.D
9.C
10.C
11.
12.9.
13.
14.2
15.
16.8
17.30
18..
19.40米
20.
21.(1)是
(2)略
22.
23.(1);(2)
24.(1)当△BDE是直角三角形时,或;(2)①当时,,
当时, ;②存在, 即当时,□CDEF为菱形.
一、单选题(共10小题,满分40分)
1.如图,在△ABC中,DE∥BC,AD:BD=5:3,BC=16,则DE的长为( )
A.6 B.8 C.10 D.12
2.如图,在平面直角坐标系中,,,将以为位似中心缩小一半,则对应的点的坐标( )
A. B.
C.或 D.或
3.如图,在平面直角坐标系中,已知点,,以原点为位似中心,相似比为,把缩小,则点的对应点的坐标是( )
A. B.
C.或 D.或
4.在平面直角坐标系中,点、点,以原点为位似中心,按的比例把缩小,则点的对应点的坐标为( )
A. B.
C.或 D.或
5.如图,在矩形ABCD中,E,F,G分别在AB,BC,CD上,DE⊥EF,EF⊥FG,BE=3,BF=2,FC=6,则DG的长是( )
A.4 B. C. D.5
6.已知与相似,且相似比是,那么它们的面积比( )
A. B. C. D.
7.《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆AB,从木杆的顶端B观察井水水岸D,视线BD与井口的直径AC交于点E,如果测得米,米,米,那么CD为( )米.
A.5 B.4 C.3 D.2
8.在△ABC中,AB=AC=1,BC=x,∠A=36°.则的值为( ).
A. B. C.1 D.
9.如图,等腰直角三角形ABC中,AB=AC=4,点P为BC边上的任意一点(不与点B、C重合),且∠APD=45°,PD交AB于点D.设BP=x,BD=y,则y关于x的函数图象大致是( )
A.B.C. D.
10.如图,在平面直角坐标系中,等边的边经过原点,且顶点,都在的图象上,顶点在的图象上,则的值为( )
A. B. C. D.
二、填空题(共8小题,满分32分)
11.如图,小明同学用自制的直角三角形纸板测量树的高度,他调整自己的位置,设法使斜边保持水平,并且边与点在同一直线上.已知纸板的两条直角边,,测得边离地面的高度,,则树高为
12.如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,则线段AC的长= .
13.如图,线段两个端点的坐标分别为、,以原点为位似中心,将线段放大得到线段,若点的坐标为,则点的坐标为 .
14.如图,D为的AB边上的一点,,若cm,cm,则AD的长为 cm.
15.已知点C是线段AB的黄金分割点(靠近A),AB=2,则BC= .
16.如图,数学活动小组为了测量学校旗杆的高度,使用长为的竹竿作为测量工具.移动竹竿,使竹顶端的影子与旗杆顶端的影子在地面处重合,测得,,则旗杆的高为 .
17.如图,在中,点D、E、F分别在边、、上,,,.如果,那么 .
18.如图所示,已知矩形ABCD的对角线相交于点O,点E、F分别是OD、OC的中点,边AD=4,DC=2,则△OEF的面积为 .
三、解答题(共6小题,每题8分,满分48分)
19.如图,为估算某河的宽度,在河对岸边选定一个目标点,在近岸取点,使得,点在上,并且点在同一条直线上.若测得米,米,米,试求河的宽度.
20.阅读下列材料,回答问题.
任务:测量一棵树的高度,该树的底端可到达,顶部不可到达,如图.
工具:一把皮尺,自制的直角三角形纸板.
测量过程:小明站在点处,调整自己的位置,使得三角尺斜边与地面平行,且边与点在同一直线上.
小亮和小颖用皮尺测量,,,点与点之间的距离.求树高.用含,,,的代数式表示)
21.阅读与思考
下面是某兴趣小组的一次实践活动记录:
兴趣小组札记
2022年×月×日,在数学兴趣小组开展的活动中,小华给每位同学发了一张扇形纸片,并要求大家按照下面的做法画出一个正方形,使得正方形的四个顶点分别落在扇形半径,和上.
小李的做法如下:如图1,先在扇形内画出正方形,使得C,D两点在上,点F在上,连接并延长交于点G,过点G分别作于点J,交于点H,再作于点I.
(1)猜想证明:请问小李画出的四边形是正方形吗?如果是,请给出你的证明;如果不是,请说明理由.
(2)实践操作:如图2,给定锐角三角形,画出一个长宽比为的矩形,使得点D,E位于边上,点F,G分别位于边,上.
22.如图,D、E分别为△ABC的AB、AC边上两点,且AD=5,BD=3,AE=4,CE=6. 求的值.
23.已知:如图
(1)如果,那么吗?为什么?
(2)如果,那么吗?为什么?
24.如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点D从点C出发,以2 cm/s 的速度沿折线C→A→B向点B运动,同时点E从点B出发,以1 cm/s的速度沿BC边向点C运动,设点E运动的时间为t (单位:s)(0<t<8).
(1) 当△BDE 是直角三角形时,求t的值;
(2)若四边形CDEF是以CD、DE为一组邻边的平行四边形,①设它的面积为S,求S关于t的函数关系式;②是否存在某个时刻t,使平行四边形CDEF为菱形 若存在,求出t的值;若不存在,请说明理由.
参考答案:
1.C
2.C
3.D
4.C
5.B
6.C
7.C
8.D
9.C
10.C
11.
12.9.
13.
14.2
15.
16.8
17.30
18..
19.40米
20.
21.(1)是
(2)略
22.
23.(1);(2)
24.(1)当△BDE是直角三角形时,或;(2)①当时,,
当时, ;②存在, 即当时,□CDEF为菱形.
