八年级数学下册试题 9.4.5 正方形的性质和判定-苏科版(含详解)
文档属性
| 名称 | 八年级数学下册试题 9.4.5 正方形的性质和判定-苏科版(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 736.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-02 00:00:00 | ||
图片预览



文档简介
9.4.5 正方形的性质和判定
一、单选题
1.下列四边形中,是中心对称图形,但不是轴对称图形的是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
2.正方形具备而菱形不具备的性质是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.每条对角线平分一组对角
3.如图,在中,点分别在边,,上,且,.下列四个判断中,不正确的是( )
A.四边形是平行四边形
B.如果,那么四边形是矩形
C.如果平分平分∠BAC,那么四边形 AEDF 是菱形
D.如果AD⊥BC 且 AB=AC,那么四边形 AEDF 是正方形
4.正方形ABCD所在平面内有一点P,使△PAB、△PBC、△PCD、△PDA都是等腰三角形,那么具有这样性质的点P共有( )
A.5个 B.7个 C.8个 D.9个
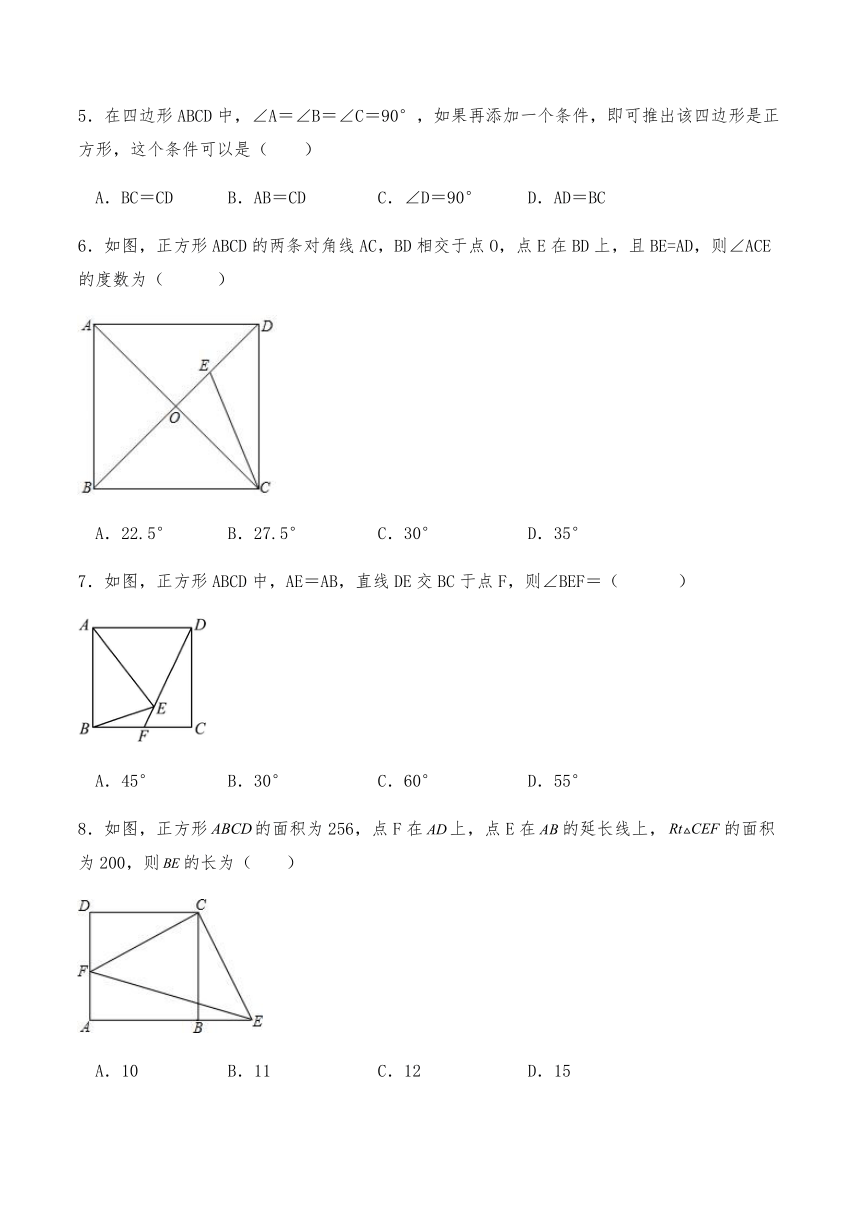
5.在四边形ABCD中,∠A=∠B=∠C=90°,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是( )
A.BC=CD B.AB=CD C.∠D=90° D.AD=BC
6.如图,正方形ABCD的两条对角线AC,BD相交于点O,点E在BD上,且BE=AD,则∠ACE的度数为( )
A.22.5° B.27.5° C.30° D.35°
7.如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )
A.45° B.30° C.60° D.55°
8.如图,正方形的面积为256,点F在上,点E在的延长线上,的面积为200,则的长为( )
A.10 B.11 C.12 D.15
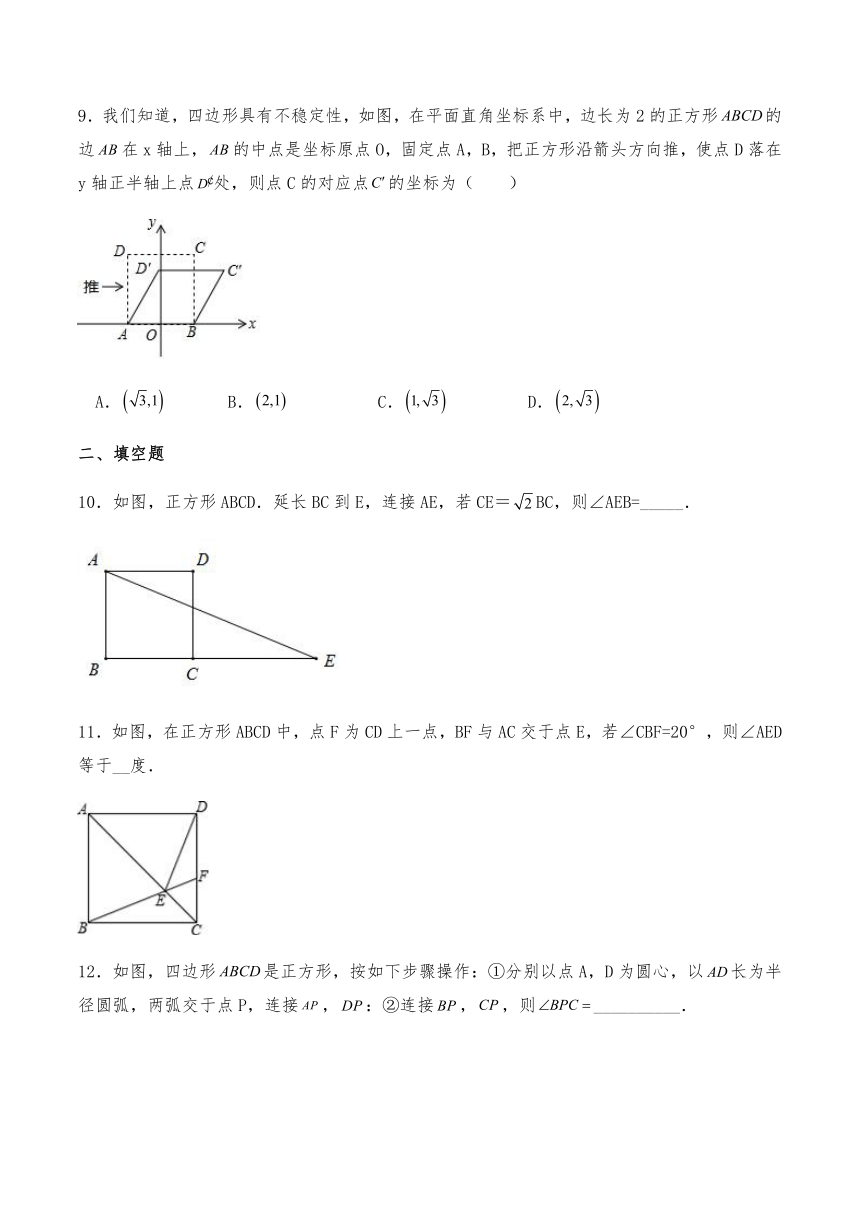
9.我们知道,四边形具有不稳定性,如图,在平面直角坐标系中,边长为2的正方形的边在x轴上,的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点处,则点C的对应点的坐标为( )
A. B. C. D.
二、填空题
10.如图,正方形ABCD.延长BC到E,连接AE,若CE=BC,则∠AEB=_____.
11.如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E,若∠CBF=20°,则∠AED等于__度.
12.如图,四边形是正方形,按如下步骤操作:①分别以点A,D为圆心,以长为半径圆弧,两弧交于点P,连接,:②连接,,则__________.
13.正方形ABCD中,AC、BD交于O,∠EOF=900,已知AE=6,CF=8,则S△BEF为__________.
14.如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线将图形分成面积相等的两部分,则直线的函数关系式为______.
15.如图,在正方形ABCD中,,E是AB的中点,P是AD上任意一点,连接PE,PC,若△PEC是等腰三角形,则AP的长可能是______.
16.如图,正方形ABCD中,AB=,O是BC边的中点,点E是正方形内一动点,OE=4,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE、CF,则线段OF长的最小值为_____
三、解答题
17.已知,如图,四边形ABCD是菱形,∠B是锐角,AF⊥BC于点F,CH⊥AD于点H,在AB边上取点E,使得AE=AH,在CD边上取点G,使得CG=CF.联结EF、FG、CH、HE.
(1)求证:四边形EFGH是矩形.
(2)若∠B=45度,求证:四边形EFGH是正方形.
18.如图,在矩形中,,分别是,的中点,,分别是,的中点.
(1)求证:;
(2)当矩形满足什么条件时,四边形为正方形?请说明理由.
19.如图,在中,是的中点,过点D作且,交于点O,连接.
(1)求证:四边形是菱形;
(2)当和满足数量关系________时,四边形是正方形.
20.如图,在平行四边形中,对角线、相交于点,是延长线上的点,且为等边三角形.
(1)四边形是菱形吗 请说明理由;
(2)若,试说明:四边形是正方形.
21.四边形 ABCD 为正方形,点 E 为线段 AC 上一点,连接 DE,过点 E 作 EF ⊥DE,交射线 BC 于点 F,以 DE、EF 为邻边作矩形 DEFG,连接 CG.
(1)如图,求证:矩形 DEFG 是正方形;
(2)若 AB=,CE=2,求 CG 的长;
(3)当线段 DE 与正方形 ABCD 的某条边的夹角是 40°时,直接写出∠EFC 的度数.
22.【基础回顾】(1)如图1,是正方形中边上任意一点,以点A为中心,将△ADE顺时针旋转90°后得到,若连接,则△AEE' 的形状为______;
【类比探究】(2)如图2,在(1)的条件下,设与相交于点,在上取点,使,连接,猜想与的数量关系,并给予证明;
【联想拓展】(3)如图3,在△ABC中,,.点在上,求,,之间存在的数量关系.
答案
一、单选题
1.A
【解析】
A、平行四边形不是轴对称图形,是中心对称图形,符合题意;
B、矩形是轴对称图形,又是中心对称图形,不符合题意;
C、菱形既是轴对称图形,又是中心对称图形,不符合题意;
D、正方形既是轴对称图形,又是中心对称图形,不符合题意.
故选A.
2.C
【解析】
解:A.平行四边形的对角线互相平分,所以菱形和正方形对角线均互相平分,故该选项不符合题意;
B. 菱形和正方形的对角线均互相垂直,故该选不项符合题意;
C. 正方形对角线相等,而菱形对角线不相等,故该选项符合题意;
D.对角线即角平分线是菱形的性质,正方形具有全部菱形的性质,故该选项不符合题意.
故选:C.
3.D
【解析】
由DE∥CA,DF∥BA,根据两组对边分别平行的四边形是平行四边形可得四边形AEDF是平行四边形;
又有∠BAC=90°,根据有一角是直角的平行四边形是矩形,可得四边形AEDF是矩形
故A. B正确;
如果AD平分∠BAC,那么∠EAD=∠FAD,又有DF∥BA,可得∠EAD=∠ADF,
∴∠FAD=∠ADF,
∴AF=FD,那么根据邻边相等的平行四边形是菱形,可得四边形AEDF是菱形故C正确;
如果AD⊥BC且AB=AC,那么AD平分∠BAC,同上可得四边形AEDF是菱形,故D错误.
故选D
4.D
【解析】
具有这样性质的点P共有9个,如图所示,
①两对角线的交点是一个;
②以正方形四个顶点为圆心,以边长为半径画圆,在正方形里面有4个交点,在外部也有4个交点,
则一共是4+4+1=9个;
故选D.
5.A
【解析】
解:∵∠A=∠B=∠C=90°,
∴四边形ABCD是矩形,
∴当BC=CD时,四边形ABCD是正方形,
其余条件均不能推导得出四边形ABCD是正方形,
故选:A.
6.A
【解析】
解:∵四边形ABCD是正方形,
∴BC=AD,∠DBC=45°,
∵BE=AD,
∴BE=BC,
∴∠BEC=∠BCE=(180°﹣45°)÷2=67.5°,
∵AC⊥BD,
∴∠COE=90°,
∴∠ACE=90°﹣∠BEC=90°﹣67.5°=22.5°,
故选:A.
7.A
【解析】
解:设∠BAE=x°,
∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
∵AE=AB,
∴AB=AE=AD,
∴∠ABE=∠AEB=(180°-∠BAE)=90°-x°,∠DAE=90°-x°,
∠AED=∠ADE=(180°-∠DAE)=[180°-(90°-x°)]=45°+x°,
∴∠BEF=180°-∠AEB-∠AED
=180°-(90°-x°)-(45°+x°)=45°.
∴∠BEF=45°.
故选:A.
8.C
【解析】
解:∵∠ECF=90°,∠DCB=90°,
∴∠BCE=∠DCF,
∴,
∴△CDF≌△CBE,故CF=CE.
因为Rt△CEF的面积是200,即
CE CF=200,故CE=20,
正方形ABCD的面积=BC2=256,得BC=16.
根据勾股定理得:BE==12.
故选:C.
9.D
【解析】
解:,
,
,
,,
,
故选:D.
二、填空题
10.22.5°
【解析】
解:如图,连接AC,
∵四边形ABCD是正方形,
∴AC=BC,∠ACB=45°,
∵CE=BC,
∴AC=CE,
∴∠AEB=∠CAE,
∵∠ACB=∠CAE+∠E=2∠AEB=45°,
∴∠AEB=22.5°.
故答案为22.5°.
11.65
【解析】
∵四边形ABCD是正方形
∴∠ACB=∠ACD=∠BAC=∠CAD=45°,∠ABC=90°,AB=AD
∵∠FBC=20°
∴∠ABF=70°
∴在△ABE中,∠AEB=65°
在△ABE与△ADE中
∴△ABE≌△ADE
∴∠AED=∠AEB=65°
故答案为:65°
12.150゜
【解析】
解:根据作图过程可知:
AD=AP=PD,
∴△ADP是等边三角形,
∴∠DAP=∠ADP=∠APD=60°,
∵四边形ABCD是正方形,
∴AB=AD=DC,∠BAD=∠ADC=∠ABC=∠BCD=90°,
∴AB=AP=DP=DC,
∴∠ABP=∠APB=∠DPC=∠DCP=75°,
∴∠BPC=360°-60°-75°-75°=150°.
故答案为:150°.
13.24
【解析】
解:∵四边形ABCD是正方形,
∴AB=BC,OA=OB,∠ABC=∠AOB=90°,∠BAC=∠CBD=45°.
∵∠EOF=90°,
∴∠AOE=∠BOF=90°-∠EOB.
在△AOE和△BOF中,
,
∴△AOE≌△BOF(ASA),
∴AE=BF=6,
∴BC=BF+FC=6+8=14,
∴AB=BC=14,
∴BE=AB -AE=14-6=8,
∴S△BEF,
故答案为24.
14.
【解析】
解:设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,过A作AC⊥y轴于C
∵正方形的边长为1,
∴OB=3
∵经过原点的一条直线l将这八个正方形分成面积相等的两部分,
∴两边分别是4,
∴三角形ABO面积是5,
∴OB AB=5,
∴AB=,
∴OC=,
由此可知直线l经过(3,),
设直线方程为y=kx,
则=3k,
k=,
∴直线l解析式为y=x.
故答案妫:y=x.
15.或或
【解析】
解:如图1,当时,
∵四边形ABCD是正方形,
∴∠B=∠D=90°,BC=DC,
∴Rt△BEC≌Rt△DPC ,
∴则,
∵E是AB的中点,
∴
∴;
如图2.当点P与点D重合时,
∵四边形ABCD是正方形,
∴AD=BC,∠A=∠B=90°,
∵E是AB的中点,
∴AE=BE,
∴△ADE≌△BCE(SAS),
∴即PE=CE,△PEC是等腰三角形.
∴;
如图3.当时,设,则,
在直角△PDC中,,
在直角△AEP中,,
则.解得,即.
综上所述,AP的长可能是1或2或.
故答案为:1或2或.
16..
【解析】
解:如图,连接DO,将线段DO绕点D逆时针旋转90°得DM,连接OF,FM,OM,
∵∠EDF=∠ODM=90°,
∴∠EDO=∠FDM,
∵DE=DF,DO=DM,
∴△EDO≌△FDM(SAS),
∴FM=OE=4,
∵正方形ABCD中,AB=,O是BC边的中点,
∴OC=,
∴OD==10,
∴OM==,
∵OF+MF≥OM,
∴OF≥,
∴线段OF长的最小值为.
故答案为:.
三、解答题
17.(1)
证明∵四边形ABCD是菱形
∴ADBC,AB=BC=CD=AD,∠BAD=∠BCD,∠ABC=∠ADC
∴∠ABC+∠BAD=180°
∵AF⊥BC ,CH⊥AD
∴∠AFC=∠AHC=90°
∵ADBC
∴ ∠FAH=180°-∠AFC=90°
∴四边形AFCH为矩形,
∴AH=CF
∵AE=AH,CG=CF
∴AH=CF=AE=CG,BF=BE=DH=DG
∴△AEH≌△CFG(SAS),△BEF≌△DGH(SAS)
∴EH=FG,EF=GH
∴四边形EFGH是平行四边形
∵BE=BF
∴△BEF是等腰三角形
∴∠BEF=∠BFE=(180°-∠ABC)=90°-∠ABC
同理可得∠AEH=∠BAD
∴∠BFE+∠AEH=(∠ABC+∠BAD)=90°
∴∠HEF=180°-(∠BFE+∠AEH)=90°
∴四边形EFGH是矩形.
(2)
证明:如图,连结BD,FH,AC,设BD、AC、FH相交于点O.
∵四边形ABCD是菱形
∴ADBC,AB=BC=CD=AD, AC⊥BD
∴∠ADB=∠CBD,△ABD是等腰三角形,∠BOC==90°
∴∠ABD=∠ADB
∴∠ABD=∠CBD=∠ABC=22.5°
∴∠BCO=180°-∠CBD -∠BOC=67.5°
∵四边形AFCH为矩形
∴OF=OC,∠AFC=90°
∴△FOC是等腰三角形
∴∠OFC=∠BCO=67.5°
∴∠AFH=∠AFC -∠OFC=22.5°
∵BE=BF
∴△BEF是等腰三角形
∴∠BEF=∠BFE=(180°-∠ABC)=90°-∠ABC=67.5°
∵AF⊥BC
∴∠AFB=90°
∴∠AFE=∠AFB -∠BFE=22.5°
∴∠EFH=∠AFE+∠AFH=45°
∵四边形EFGH是矩形
∴∠FEH=90°
∴∠EHF=180-∠FEH-∠EFH=45°
∴∠EFH=∠EHF
∴EF=EH
∴四边形EFGH是正方形.
18.(1)
∵四边形是矩形
∴,,
∵,分别是,的中点
∴,
∴,且∠ABC=∠CDE=90°,AB=CD,
∴
∴
(2)
当矩形满足时,四边形为正方形
连接
∵四边形是矩形
∴
∵,分别是,的中点
∴,
∵
∴
∵,
∴四边形是平行四边形
∵
∴平行四边形是矩形
∵,
∴
∴矩形是正方形
同理可证,四边形是正方形
∴,,,
∴和为等腰直角三角形
∵,分别是,的中点
∴,,
∴
∴四边形是菱形
∵
∴
∴菱形是正方形
19.(1)证明:,
∴四边形是平行四边形.
.
∵D是的中点,.
.
,∴四边形是平行四边形.
,
,即.
是菱形.
(2)解:,理由如下:
∵∠ACB=90°,AB=AC,
∴∠ABC=45°,
∵∠CBE=∠ABC,
∴∠DBE=90°,
∵四边形BECD是菱形,
∴四边形BECD是正方形,
故答案为:AB=AC.
20.(1)四边形为菱形,理由:
在平行四边形中,,
是等边三角形.
,
又、、、四点在一条直线上,
.
平行四边形是菱形. (对角线互相垂直的平行四边形是菱形)
(2)由是等边三角形,,得到,
.
.
,
四边形是菱形,
,
,
四边形是正方形.(有一个角是90°的菱形是正方形)
21.(1)
证明:如下图所示:
作EP⊥CD于P,EQ⊥BC于Q,
∵∠DCA=∠BCA,
∴EQ=EP,
∵∠QEF+∠FEC=90°,∠PED+∠FEC=90°,
∴∠QEF=∠PED,
在Rt△EQF和Rt△EPD中,
,
∴Rt△EQF≌Rt△EPD(ASA),
∴EF=ED,
∴矩形DEFG是正方形;
(2)
如图2:
在Rt△ABC中AC=AB=,
∵EC=2,
∴AE=CE,
∴点F与C重合,此时△DCG是等腰直角三角形,
∴;
(3)
①如图3:
当DE与AD的夹角为40°时,
∠DEC=45°+40°=85°,
∵∠DEF=90°,
∴∠CEF=5°,
∵∠ECF=45°,
∴∠EFC=130°,
②如图4:
当DE与DC的夹角为40°时,
∵∠DEF=∠DCF=90°,
∴∠EFC=∠EDC=40°,
综上所述,∠EFC=130°或40°.
22.解(1)∵四边形ABCD为正方形,
∴AD=AB,∠DAB=90°,∠D=90°,
∵△ADE顺时针旋转90°,得△ABE′,
∴∠EAE′=∠DAB=90°,E′A=EA,
∴△AEE′为等腰直角三角形;
故答案为:等腰直角三角形;
(2)QE=E'P.
证明:∵将△ADE顺时针旋转90°后得到△ABE′,
∴∠D=∠ABE',DE=BE',
∵DQ=BP,
∴△DQE≌△BE'P(SAS),
∴QE=E'P.
(3)将△ABP逆时针旋转90°后得到△ACD,连接PD,则△APD是等腰直角三角形,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
由旋转的性质可知∠ABP=∠ACD=45°,BP=CD,
∵∠ACB=45°,
∴∠BCD=∠ACB+∠ACD=90°,
∴PC2+CD2=PD2,
∵AP2+AD2=PD2=2AP2,
∴PC2+BP2=2AP2.
故答案为:PC2+BP2=2AP2.
一、单选题
1.下列四边形中,是中心对称图形,但不是轴对称图形的是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
2.正方形具备而菱形不具备的性质是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.每条对角线平分一组对角
3.如图,在中,点分别在边,,上,且,.下列四个判断中,不正确的是( )
A.四边形是平行四边形
B.如果,那么四边形是矩形
C.如果平分平分∠BAC,那么四边形 AEDF 是菱形
D.如果AD⊥BC 且 AB=AC,那么四边形 AEDF 是正方形
4.正方形ABCD所在平面内有一点P,使△PAB、△PBC、△PCD、△PDA都是等腰三角形,那么具有这样性质的点P共有( )
A.5个 B.7个 C.8个 D.9个
5.在四边形ABCD中,∠A=∠B=∠C=90°,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是( )
A.BC=CD B.AB=CD C.∠D=90° D.AD=BC
6.如图,正方形ABCD的两条对角线AC,BD相交于点O,点E在BD上,且BE=AD,则∠ACE的度数为( )
A.22.5° B.27.5° C.30° D.35°
7.如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )
A.45° B.30° C.60° D.55°
8.如图,正方形的面积为256,点F在上,点E在的延长线上,的面积为200,则的长为( )
A.10 B.11 C.12 D.15
9.我们知道,四边形具有不稳定性,如图,在平面直角坐标系中,边长为2的正方形的边在x轴上,的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点处,则点C的对应点的坐标为( )
A. B. C. D.
二、填空题
10.如图,正方形ABCD.延长BC到E,连接AE,若CE=BC,则∠AEB=_____.
11.如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E,若∠CBF=20°,则∠AED等于__度.
12.如图,四边形是正方形,按如下步骤操作:①分别以点A,D为圆心,以长为半径圆弧,两弧交于点P,连接,:②连接,,则__________.
13.正方形ABCD中,AC、BD交于O,∠EOF=900,已知AE=6,CF=8,则S△BEF为__________.
14.如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线将图形分成面积相等的两部分,则直线的函数关系式为______.
15.如图,在正方形ABCD中,,E是AB的中点,P是AD上任意一点,连接PE,PC,若△PEC是等腰三角形,则AP的长可能是______.
16.如图,正方形ABCD中,AB=,O是BC边的中点,点E是正方形内一动点,OE=4,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE、CF,则线段OF长的最小值为_____
三、解答题
17.已知,如图,四边形ABCD是菱形,∠B是锐角,AF⊥BC于点F,CH⊥AD于点H,在AB边上取点E,使得AE=AH,在CD边上取点G,使得CG=CF.联结EF、FG、CH、HE.
(1)求证:四边形EFGH是矩形.
(2)若∠B=45度,求证:四边形EFGH是正方形.
18.如图,在矩形中,,分别是,的中点,,分别是,的中点.
(1)求证:;
(2)当矩形满足什么条件时,四边形为正方形?请说明理由.
19.如图,在中,是的中点,过点D作且,交于点O,连接.
(1)求证:四边形是菱形;
(2)当和满足数量关系________时,四边形是正方形.
20.如图,在平行四边形中,对角线、相交于点,是延长线上的点,且为等边三角形.
(1)四边形是菱形吗 请说明理由;
(2)若,试说明:四边形是正方形.
21.四边形 ABCD 为正方形,点 E 为线段 AC 上一点,连接 DE,过点 E 作 EF ⊥DE,交射线 BC 于点 F,以 DE、EF 为邻边作矩形 DEFG,连接 CG.
(1)如图,求证:矩形 DEFG 是正方形;
(2)若 AB=,CE=2,求 CG 的长;
(3)当线段 DE 与正方形 ABCD 的某条边的夹角是 40°时,直接写出∠EFC 的度数.
22.【基础回顾】(1)如图1,是正方形中边上任意一点,以点A为中心,将△ADE顺时针旋转90°后得到,若连接,则△AEE' 的形状为______;
【类比探究】(2)如图2,在(1)的条件下,设与相交于点,在上取点,使,连接,猜想与的数量关系,并给予证明;
【联想拓展】(3)如图3,在△ABC中,,.点在上,求,,之间存在的数量关系.
答案
一、单选题
1.A
【解析】
A、平行四边形不是轴对称图形,是中心对称图形,符合题意;
B、矩形是轴对称图形,又是中心对称图形,不符合题意;
C、菱形既是轴对称图形,又是中心对称图形,不符合题意;
D、正方形既是轴对称图形,又是中心对称图形,不符合题意.
故选A.
2.C
【解析】
解:A.平行四边形的对角线互相平分,所以菱形和正方形对角线均互相平分,故该选项不符合题意;
B. 菱形和正方形的对角线均互相垂直,故该选不项符合题意;
C. 正方形对角线相等,而菱形对角线不相等,故该选项符合题意;
D.对角线即角平分线是菱形的性质,正方形具有全部菱形的性质,故该选项不符合题意.
故选:C.
3.D
【解析】
由DE∥CA,DF∥BA,根据两组对边分别平行的四边形是平行四边形可得四边形AEDF是平行四边形;
又有∠BAC=90°,根据有一角是直角的平行四边形是矩形,可得四边形AEDF是矩形
故A. B正确;
如果AD平分∠BAC,那么∠EAD=∠FAD,又有DF∥BA,可得∠EAD=∠ADF,
∴∠FAD=∠ADF,
∴AF=FD,那么根据邻边相等的平行四边形是菱形,可得四边形AEDF是菱形故C正确;
如果AD⊥BC且AB=AC,那么AD平分∠BAC,同上可得四边形AEDF是菱形,故D错误.
故选D
4.D
【解析】
具有这样性质的点P共有9个,如图所示,
①两对角线的交点是一个;
②以正方形四个顶点为圆心,以边长为半径画圆,在正方形里面有4个交点,在外部也有4个交点,
则一共是4+4+1=9个;
故选D.
5.A
【解析】
解:∵∠A=∠B=∠C=90°,
∴四边形ABCD是矩形,
∴当BC=CD时,四边形ABCD是正方形,
其余条件均不能推导得出四边形ABCD是正方形,
故选:A.
6.A
【解析】
解:∵四边形ABCD是正方形,
∴BC=AD,∠DBC=45°,
∵BE=AD,
∴BE=BC,
∴∠BEC=∠BCE=(180°﹣45°)÷2=67.5°,
∵AC⊥BD,
∴∠COE=90°,
∴∠ACE=90°﹣∠BEC=90°﹣67.5°=22.5°,
故选:A.
7.A
【解析】
解:设∠BAE=x°,
∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
∵AE=AB,
∴AB=AE=AD,
∴∠ABE=∠AEB=(180°-∠BAE)=90°-x°,∠DAE=90°-x°,
∠AED=∠ADE=(180°-∠DAE)=[180°-(90°-x°)]=45°+x°,
∴∠BEF=180°-∠AEB-∠AED
=180°-(90°-x°)-(45°+x°)=45°.
∴∠BEF=45°.
故选:A.
8.C
【解析】
解:∵∠ECF=90°,∠DCB=90°,
∴∠BCE=∠DCF,
∴,
∴△CDF≌△CBE,故CF=CE.
因为Rt△CEF的面积是200,即
CE CF=200,故CE=20,
正方形ABCD的面积=BC2=256,得BC=16.
根据勾股定理得:BE==12.
故选:C.
9.D
【解析】
解:,
,
,
,,
,
故选:D.
二、填空题
10.22.5°
【解析】
解:如图,连接AC,
∵四边形ABCD是正方形,
∴AC=BC,∠ACB=45°,
∵CE=BC,
∴AC=CE,
∴∠AEB=∠CAE,
∵∠ACB=∠CAE+∠E=2∠AEB=45°,
∴∠AEB=22.5°.
故答案为22.5°.
11.65
【解析】
∵四边形ABCD是正方形
∴∠ACB=∠ACD=∠BAC=∠CAD=45°,∠ABC=90°,AB=AD
∵∠FBC=20°
∴∠ABF=70°
∴在△ABE中,∠AEB=65°
在△ABE与△ADE中
∴△ABE≌△ADE
∴∠AED=∠AEB=65°
故答案为:65°
12.150゜
【解析】
解:根据作图过程可知:
AD=AP=PD,
∴△ADP是等边三角形,
∴∠DAP=∠ADP=∠APD=60°,
∵四边形ABCD是正方形,
∴AB=AD=DC,∠BAD=∠ADC=∠ABC=∠BCD=90°,
∴AB=AP=DP=DC,
∴∠ABP=∠APB=∠DPC=∠DCP=75°,
∴∠BPC=360°-60°-75°-75°=150°.
故答案为:150°.
13.24
【解析】
解:∵四边形ABCD是正方形,
∴AB=BC,OA=OB,∠ABC=∠AOB=90°,∠BAC=∠CBD=45°.
∵∠EOF=90°,
∴∠AOE=∠BOF=90°-∠EOB.
在△AOE和△BOF中,
,
∴△AOE≌△BOF(ASA),
∴AE=BF=6,
∴BC=BF+FC=6+8=14,
∴AB=BC=14,
∴BE=AB -AE=14-6=8,
∴S△BEF,
故答案为24.
14.
【解析】
解:设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,过A作AC⊥y轴于C
∵正方形的边长为1,
∴OB=3
∵经过原点的一条直线l将这八个正方形分成面积相等的两部分,
∴两边分别是4,
∴三角形ABO面积是5,
∴OB AB=5,
∴AB=,
∴OC=,
由此可知直线l经过(3,),
设直线方程为y=kx,
则=3k,
k=,
∴直线l解析式为y=x.
故答案妫:y=x.
15.或或
【解析】
解:如图1,当时,
∵四边形ABCD是正方形,
∴∠B=∠D=90°,BC=DC,
∴Rt△BEC≌Rt△DPC ,
∴则,
∵E是AB的中点,
∴
∴;
如图2.当点P与点D重合时,
∵四边形ABCD是正方形,
∴AD=BC,∠A=∠B=90°,
∵E是AB的中点,
∴AE=BE,
∴△ADE≌△BCE(SAS),
∴即PE=CE,△PEC是等腰三角形.
∴;
如图3.当时,设,则,
在直角△PDC中,,
在直角△AEP中,,
则.解得,即.
综上所述,AP的长可能是1或2或.
故答案为:1或2或.
16..
【解析】
解:如图,连接DO,将线段DO绕点D逆时针旋转90°得DM,连接OF,FM,OM,
∵∠EDF=∠ODM=90°,
∴∠EDO=∠FDM,
∵DE=DF,DO=DM,
∴△EDO≌△FDM(SAS),
∴FM=OE=4,
∵正方形ABCD中,AB=,O是BC边的中点,
∴OC=,
∴OD==10,
∴OM==,
∵OF+MF≥OM,
∴OF≥,
∴线段OF长的最小值为.
故答案为:.
三、解答题
17.(1)
证明∵四边形ABCD是菱形
∴ADBC,AB=BC=CD=AD,∠BAD=∠BCD,∠ABC=∠ADC
∴∠ABC+∠BAD=180°
∵AF⊥BC ,CH⊥AD
∴∠AFC=∠AHC=90°
∵ADBC
∴ ∠FAH=180°-∠AFC=90°
∴四边形AFCH为矩形,
∴AH=CF
∵AE=AH,CG=CF
∴AH=CF=AE=CG,BF=BE=DH=DG
∴△AEH≌△CFG(SAS),△BEF≌△DGH(SAS)
∴EH=FG,EF=GH
∴四边形EFGH是平行四边形
∵BE=BF
∴△BEF是等腰三角形
∴∠BEF=∠BFE=(180°-∠ABC)=90°-∠ABC
同理可得∠AEH=∠BAD
∴∠BFE+∠AEH=(∠ABC+∠BAD)=90°
∴∠HEF=180°-(∠BFE+∠AEH)=90°
∴四边形EFGH是矩形.
(2)
证明:如图,连结BD,FH,AC,设BD、AC、FH相交于点O.
∵四边形ABCD是菱形
∴ADBC,AB=BC=CD=AD, AC⊥BD
∴∠ADB=∠CBD,△ABD是等腰三角形,∠BOC==90°
∴∠ABD=∠ADB
∴∠ABD=∠CBD=∠ABC=22.5°
∴∠BCO=180°-∠CBD -∠BOC=67.5°
∵四边形AFCH为矩形
∴OF=OC,∠AFC=90°
∴△FOC是等腰三角形
∴∠OFC=∠BCO=67.5°
∴∠AFH=∠AFC -∠OFC=22.5°
∵BE=BF
∴△BEF是等腰三角形
∴∠BEF=∠BFE=(180°-∠ABC)=90°-∠ABC=67.5°
∵AF⊥BC
∴∠AFB=90°
∴∠AFE=∠AFB -∠BFE=22.5°
∴∠EFH=∠AFE+∠AFH=45°
∵四边形EFGH是矩形
∴∠FEH=90°
∴∠EHF=180-∠FEH-∠EFH=45°
∴∠EFH=∠EHF
∴EF=EH
∴四边形EFGH是正方形.
18.(1)
∵四边形是矩形
∴,,
∵,分别是,的中点
∴,
∴,且∠ABC=∠CDE=90°,AB=CD,
∴
∴
(2)
当矩形满足时,四边形为正方形
连接
∵四边形是矩形
∴
∵,分别是,的中点
∴,
∵
∴
∵,
∴四边形是平行四边形
∵
∴平行四边形是矩形
∵,
∴
∴矩形是正方形
同理可证,四边形是正方形
∴,,,
∴和为等腰直角三角形
∵,分别是,的中点
∴,,
∴
∴四边形是菱形
∵
∴
∴菱形是正方形
19.(1)证明:,
∴四边形是平行四边形.
.
∵D是的中点,.
.
,∴四边形是平行四边形.
,
,即.
是菱形.
(2)解:,理由如下:
∵∠ACB=90°,AB=AC,
∴∠ABC=45°,
∵∠CBE=∠ABC,
∴∠DBE=90°,
∵四边形BECD是菱形,
∴四边形BECD是正方形,
故答案为:AB=AC.
20.(1)四边形为菱形,理由:
在平行四边形中,,
是等边三角形.
,
又、、、四点在一条直线上,
.
平行四边形是菱形. (对角线互相垂直的平行四边形是菱形)
(2)由是等边三角形,,得到,
.
.
,
四边形是菱形,
,
,
四边形是正方形.(有一个角是90°的菱形是正方形)
21.(1)
证明:如下图所示:
作EP⊥CD于P,EQ⊥BC于Q,
∵∠DCA=∠BCA,
∴EQ=EP,
∵∠QEF+∠FEC=90°,∠PED+∠FEC=90°,
∴∠QEF=∠PED,
在Rt△EQF和Rt△EPD中,
,
∴Rt△EQF≌Rt△EPD(ASA),
∴EF=ED,
∴矩形DEFG是正方形;
(2)
如图2:
在Rt△ABC中AC=AB=,
∵EC=2,
∴AE=CE,
∴点F与C重合,此时△DCG是等腰直角三角形,
∴;
(3)
①如图3:
当DE与AD的夹角为40°时,
∠DEC=45°+40°=85°,
∵∠DEF=90°,
∴∠CEF=5°,
∵∠ECF=45°,
∴∠EFC=130°,
②如图4:
当DE与DC的夹角为40°时,
∵∠DEF=∠DCF=90°,
∴∠EFC=∠EDC=40°,
综上所述,∠EFC=130°或40°.
22.解(1)∵四边形ABCD为正方形,
∴AD=AB,∠DAB=90°,∠D=90°,
∵△ADE顺时针旋转90°,得△ABE′,
∴∠EAE′=∠DAB=90°,E′A=EA,
∴△AEE′为等腰直角三角形;
故答案为:等腰直角三角形;
(2)QE=E'P.
证明:∵将△ADE顺时针旋转90°后得到△ABE′,
∴∠D=∠ABE',DE=BE',
∵DQ=BP,
∴△DQE≌△BE'P(SAS),
∴QE=E'P.
(3)将△ABP逆时针旋转90°后得到△ACD,连接PD,则△APD是等腰直角三角形,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
由旋转的性质可知∠ABP=∠ACD=45°,BP=CD,
∵∠ACB=45°,
∴∠BCD=∠ACB+∠ACD=90°,
∴PC2+CD2=PD2,
∵AP2+AD2=PD2=2AP2,
∴PC2+BP2=2AP2.
故答案为:PC2+BP2=2AP2.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
