八年级数学下册试题 7.4 频数分布表和频数分布直方图-苏科版(含详解)
文档属性
| 名称 | 八年级数学下册试题 7.4 频数分布表和频数分布直方图-苏科版(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 545.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-02 07:26:24 | ||
图片预览



文档简介
7.4 频数分布表和频数分布直方图
一、单选题
1.市某视力健康管理中心对全市初中生的视力情况进行了一次抽样调查,如图是利用调查所得数据绘制的频数直方图,则这组数据的组数与组距分别是( )
A.4和0.20 B.4和0.30 C.5和0.20 D.5和0.30
2.为了检查近期期末复习的教学效果,某班数学老师把期末测评成绩进行了统计,得到如下的频数分布直方图.下列说法错误的是( )
A.成绩x在70≤x<80范围内的人数最多
B.数学老师按成绩范围分成了5组,组距是10
C.及格(60分以上)的人数有34人
D.全班一共有40人
3.在样本频数分布直方图中,有11个小长方形,若中间的小长方形的面积等于其他10个小长方形面积之和的,且中间一组的频数为40,则样本容量为( )
A.0.2 B.160 C.0.25 D.200
4.已知一组数据有80个,其中最大值为140,最小值为40,取组距为10,则可分成( ).
A.11组 B.9组 C.8组 D.10组
5.学校七年级学生做校服,校服分小号、中号、大号、特大号四种,随抽取若干名学生调查身高得如下统计分布表:
型号 身高x/cm 人数 频率
小号 145≤x<155 20 0.2
中号 155≤x<165 a 0.45
大号 165≤x<175 30 b
特大号 175≤x<185 5 0.05
求a= ,b= .( )
A.45 0.3 B.25 0.3 C.45 0.03 D.35 0.3
6.某班有48名同学,在一次数学检测中,分数均为整数,其成绩绘制成的频数直方图如图所示,从左到右的小长方形的高度比是1:3:6:4:2,则分数在70.5~80.5之间的人数是( )
A.12 B.16 C.24 D.18
7.为了了解某校七年级学生的体能情况,随机调查了其中100名学生,测试学生在1分钟内跳绳的次数,并绘制成如图所示的频数分布直方图.请根据图形计算,跳绳次数(x)在120≤x<200范围内人数占抽查学生总人数的百分比为( )
A.43% B.50% C.57% D.73%
8.数学老师将本班学生的身高数据(精确到1厘米)交给甲、乙两同学,要求他们各自绘制一幅频数分布直方图.经确认,甲绘制的图是正确的,乙在整理时漏了一个数据.由此可判断,下列说法错误的是( )
A.该班共有学生60人
B.乙在整理时遗漏的数据一定在169.5-173.5这个范围内
C.某同学身高155厘米,那么班上恰有10人比他矮
D.某同学身高165厘米,那么班上比他高的人数不超过全班人数的25%
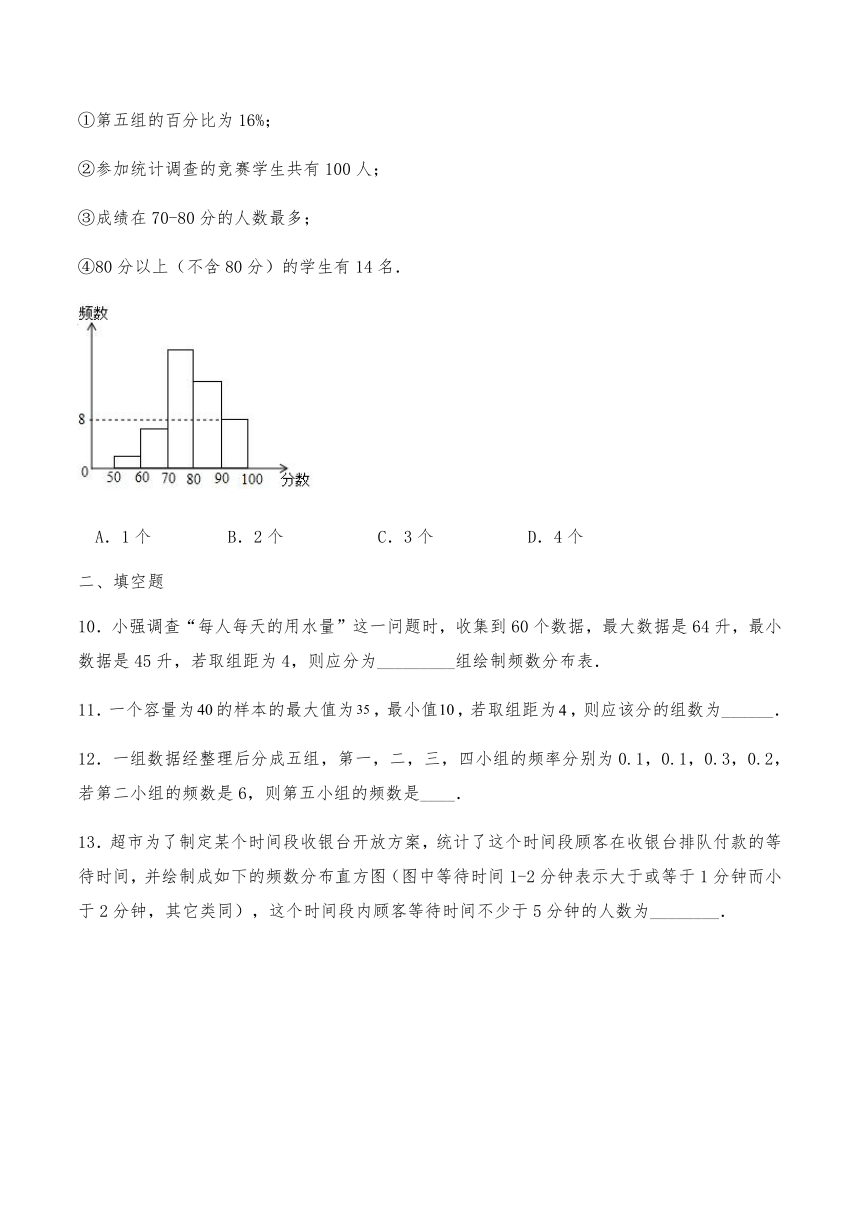
9.某校组织学生参加安全知识竞赛,并抽取部分学生成绩绘制成如图所示的统计图(每组不包括最小值,包括最大值),图中从左至右前四组的百分比分别是,第五组的频数是8.下列判断正确的有( )
①第五组的百分比为16%;
②参加统计调查的竞赛学生共有100人;
③成绩在70-80分的人数最多;
④80分以上(不含80分)的学生有14名.
A.1个 B.2个 C.3个 D.4个
二、填空题
10.小强调查“每人每天的用水量”这一问题时,收集到60个数据,最大数据是64升,最小数据是45升,若取组距为4,则应分为_________组绘制频数分布表.
11.一个容量为的样本的最大值为,最小值,若取组距为,则应该分的组数为______.
12.一组数据经整理后分成五组,第一,二,三,四小组的频率分别为0.1,0.1,0.3,0.2,若第二小组的频数是6,则第五小组的频数是____.
13.超市为了制定某个时间段收银台开放方案,统计了这个时间段顾客在收银台排队付款的等待时间,并绘制成如下的频数分布直方图(图中等待时间1-2分钟表示大于或等于1分钟而小于2分钟,其它类同),这个时间段内顾客等待时间不少于5分钟的人数为________.
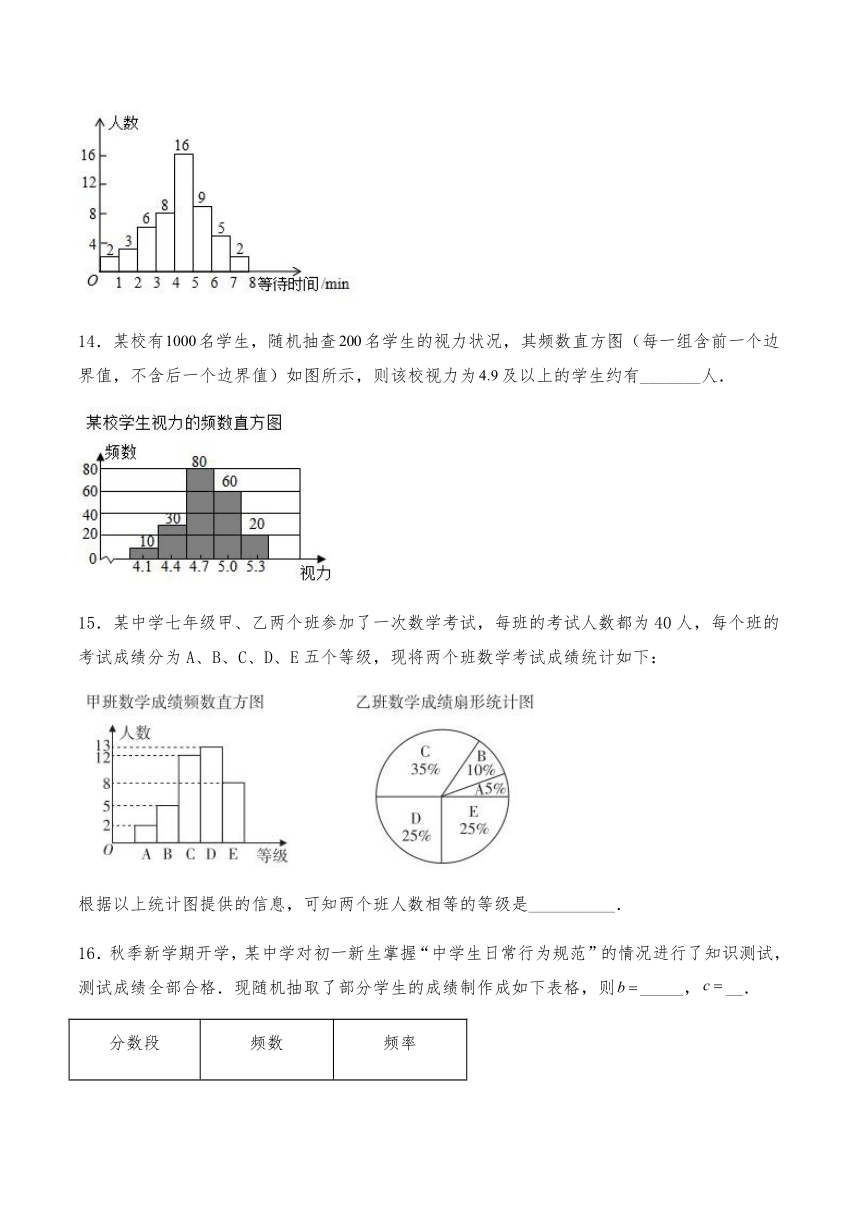
14.某校有名学生,随机抽查名学生的视力状况,其频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,则该校视力为及以上的学生约有_______人.
15.某中学七年级甲、乙两个班参加了一次数学考试,每班的考试人数都为40人,每个班的考试成绩分为A、B、C、D、E五个等级,现将两个班数学考试成绩统计如下:
根据以上统计图提供的信息,可知两个班人数相等的等级是__________.
16.秋季新学期开学,某中学对初一新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格.现随机抽取了部分学生的成绩制作成如下表格,则_____,__.
分数段 频数 频率
6
20 0.4
15
0.18
三、解答题
17.下面是2023年全国一些省(自治区、直辖市)的城市园林绿地面积(单位:).
北京 61595 上海 116929 湖北 54884 云南 22372
天津 17369 江苏 214989 湖南 42940 西藏 2174
河北 60923 浙江 74362 广东 401604 陕西 23426
山西 27973 安徽 67269 广西5 57812 甘肃 14702
内蒙古 29585 福建 41330 海南 48947 青海 3290
辽宁 84145 江西 37596 重庆 32451 宁夏 14525
吉林 34755 山东 146993 四川 66817 新疆 36359
黑龙江 64234 河南 62947 贵州 27771
根据上面提供的数据分析2023年这些地区的城市园林绿地面积的分布情况图.
18.某市在实施居民用水定额管理前,对居民生活用水情况进行了调查下表是通过简单随机抽样调查获得的50个家庭去年的月均用水量(单位:)
4.7 2.0 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.0 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 8.3 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
(1)请选择合适的组距和组数,列出样本频数分布表,画出频数分布直方图.从直方图中你能得到什么信息?
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使60%的家庭水费支出不受影响,你觉得家庭月均用水量应该定为多少?为什么?
19.某校组织了一次“疫情防控知识”专题网上学习,并进行了一次全校名学生都参加的网上测试.阅卷后,教务处随机抽取份答卷进行分析统计,绘制了频数分布表和频数分布直方图(不完整),请结合图表信息回答下列问题:
成绩(分) 频数(人) 频率
合计
(Ⅰ)_______,_______,_______,频率分布表的组距是_______;
(Ⅱ)补全频数分布直方图;
(Ⅲ)全校学生参加网上测试,成绩在范围内的学生约有多少人?
20.某学校在本学期开展数学拓展活动,为了解开展数学拓展活动后学生不同阶段的学习效果,决定随机抽取七年级部分学生进行两次跟踪测评(两次随机抽取的学生人数相同),第一次是开展数学拓展活动初期的学习质量测评,第二次是开展数学拓展活动个月后的学习质量测评.根据测评的数学成绩制作了第一次测评的数学成绩频数分布直方图(如图,每一组包括左边端点,不包括右边端点)和第二次测评的数学成绩频数分布表(如表).
第二次测评的数学成绩频数分布表:
成绩
频数
根据以上图表信息,完成下列问题:
第一次测评的数学成绩频数分布直方图
(1)______;
(2)若分及以上为优秀.
①开展数学拓展活动个月后,请估计该校名七年级学生数学成绩优秀的人数;
②请分别计算两次测评数学成绩的优秀率,并对开展数学拓展活动的效果进行分析.
21.体育老师统计了全班同学60秒跳绳的次数,并列出下面的频数分布表:
次数 60≤x<80 80≤x<100 100≤x<120 120≤x<140 140≤x<160 160≤x<180
频数 4 13 19 7 5 2
请你结合表中所给信息解答下列问题:
(1)全班有 名学生;
(2)组距是 ,组数是 ;
(3)跳绳次数x在100≤x<140范国的学生占全班学生的 %;
(4)请把频数分布直方图补充完整.
22.某学校在暑假期间安排了“心怀感恩 孝敬父母”的实践活动,倡导学生在假期中多帮父母干家务.开学以后,校学生会的老师们在学校随机抽取了部分学生,就暑假期间“平均每天帮助父母干家务所用时长”进行了调查,以下是根据相关数据绘制的统计图的一部分(每段时长均含最小值,不含最大值):
根据上述信息,回答下列问题:
(1)在本次随机抽取的样本中,调查的学生人数是 人;
(2)补全扇形统计图,补全频数分布直方图;
(3)在扇形统计图中,计算出“10 ~ 20分钟”部分所对应的圆心角的度数;
(4)如果该校共有学生3000人,请你估计“平均每天帮助父母干家务的时长不少于30分钟”的学生大约有多少人?
答案
一、单选题
1.D
【解析】解:观察图形可得:有五组数据,因此组数为5;
组距=4.253.95=0.30
故答案选D
2.C
【解析】解:A、成绩x在70≤x<80范围内有14人,人数最多,说法正确;
B、数学老师按成绩范围分成了5组,组距是10,说法正确;
C、及格(60分以上)的人数有36人,说法错误;
D、全班一共有40人,说法正确.
故选:C.
3.D
【解析】
解:所有长方形的面积和为1,又因为中间小长方形的面积是其余10个小长方形面积之和的,所以中间的面积为,
即频率为0.20,且中间一组的频数为40,所以样本容量为200,
故选:D.
4.A
【解析】解:由组数=(最大值-最小值)÷组距可得:
组数=(140-40)÷10+1=11,
故选择:A
5.A
【解析】
观察统计表知:小组的频数20,频率0.2,
∴学生总数为20÷0.2=100(人);∴,
∴,
故选:A.
6.D
【解析】
解:分数在70.5到80.5之间的人数是:×48=18(人);
故选:D.
7.C
【解析】解:总人数为10+33+40+17=100人,
120≤x<200范围内人数为40+17=57人,
在120≤x<200范围内人数占抽查学生总人数的百分比为=57%
故选:C.
8.B
【解析】
解:根据甲绘制的统计图,可知该班共有学生10+15+20+10+5=60(人),故A正确,不符合题意;
根据甲绘制的统计图,可知该班身高小于154.5的学生有10人,故C正确,不符合题意;
根据甲绘制的统计图,可知该班身高大于或等于165的学生有15人,,故D正确,不符合题意;
根据甲的直方图能够得出身高在(169.5﹣174.5)cm之间的人数为5人,从乙图中发现,身高在(169.5﹣173.5)cm的人数是4人,因此,乙在整理时遗漏的数据一定在169.5-174.5这个范围内,故B错误,符合题意;
故选B.
9.B
【解析】
解:由1-4%-12%-40%-28%=16%可知①正确;
由可知参加统计调查的竞赛学生共有50人,∴②错误;
由频数分布直方图可以得知成绩在70-80分的人数最多,∴③正确;
由可知80分以上(不含80分)的学生有22名,④错误;
故选B.
二、填空题
10.5
【解析】
解:应分(64-45)÷4=4.75,
∵第一组的下限应低于最小变量值,最后一组的上限应高于最大变量值,
∴应分5组.
故本题答案为:5.
11.7
【解析】
解:这个样本的最大值与最小值的差为,
∵组距为4,且,
∴应该分的组数为7,
故答案为:7.
12.18
【解析】解:根据题意,得:
第五小组的频率是1-0.1-0.1-0.3-0.2=0.3
已知第二小组的频数是6,频率是0.1
则这组数据共有
第五小组的频数是:60×0.3=18
故答案为:18
13.16
【解析】解:由频数分布直方图可得,
这个时间段内顾客等待时间不少于5分钟的人数为:9+5+2=16,
故答案为:16.
14.400
【解析】解:由题意得:1000×=400(人),
即该校视力为4.9及以上的学生约有400人,
故答案为:400.
15.A
【解析】解:甲班各等级人数分别为:A等级:2人;B等级:5人;C等级:12人;D等级:13人;E等级:8人;
乙班各等级人数:A等级:40×5%=2人;
B等级:40×10%=4人;
C等级:40×35%=14人;
D、E等级:40×25%=10人;
所以两个班A等级的人数相等,
故答案为:A.
16.0.3 9
【解析】
抽取的学生总数是:(人,
;;
故答案为:0.3,9.
三、解答题
17.
解:首先计算最大值和最小值,在表中的数据中,最小值是2174,最大值是401604,它们的差是399430,说明城市园林绿地面积的变化范围是399430hm2.
根据上面的计算结果,把所有的数据进行分组.如果从最小值起每隔40000hm2作为一组,则,所以要将数据分成十组:
2174≤x<42174,42174≤x<82174,
82174≤x<122174,122174≤x<162174,
162174≤x<202174,202174≤x<242174,
242174≤x<282174,282174≤x<322174,
322174≤x<362174,362174≤x<402174.
列频数分布表:
画频数分布直方图:
由上表和直方图可以看出,2009年城市园林绿地面积大部分落在2174hm2至122174hm2之间,其他区域较少.其中绿地面积在2174hm2至42174hm2的城市最多,有15个,而绿地面积在242174hm2至401274hm2范围内的很少,只有1个城市.
根据上面的分析可以看出,2009年大部分城市的园林绿地面积都比较少,城市园林绿地面积的差距很大.从一个方面说明我国的城市园林绿地面积比较小,其中中型的城市园林绿地面积有待进一步加大.
18.
(1)选组距为1,组数为7.频数分布表为:
月均用水量 划记 频数 百分比
4 8%
正正丅 12 24%
正正 14 28%
正 9 18%
正一 6 12%
3 6%
丅 2 4%
合计 50 100%
频数分布直方图为:
从直方图中得到,月均用水量处于4至5t的最多,月均用水量处于8至9t的最少.
(2)标准定为.因为50个家庭的数据是通过简单随机抽样获得的,样本中家庭月均用水量不超过的占60%,由样本估计总体,可以推断约60%的家庭水费支出不受影响.
19.
(1)a=100×0.1=10,
b=100 10 18 35 12=25,
n=25÷100=0.25.
由图可得频率分布表的组距是10
故答案为:10,25,0.25,10;
(2)如图,即为补充完整的频数分布直方图
(3)成绩在范围内的学生约有2500×=1175(人).
20.
解:(1)由第一次测评的数学成绩频数分布直方图可知参与总人数为:
(人),
根据两次开展数学拓展活动的人数相同,
,
故答案是:;
(2)①根据第二次测评的数学成绩频数分布表,
可知分及以上人数为:(人),
优秀率为:,
该校名七年级学生数学成绩优秀的人数为:(人);
②根据第一次测评的数学成绩频数分布直方图,
可知分及以上人数为:(人),
优秀率为:,
由(2)①得第二次测评的数学成绩优秀率为:,
,
开展数学拓展活动对学生的学习质量有提升作用.
21.
解:(1)全班学生人数为:(人;
(2)组距是20,组数是6;
(3)跳绳次数在范围的学生占全班学生的百分比为,
故答案是:52;
(4)如图所示:
22.
解:(1)调查的学生人数是:40÷20%=200(人),
故答案是:200;
(2) 3040分钟50÷200×100%=25%;
40~50分钟的人数所占的百分比是10 ÷200×100%=5%,
则20~30分钟所占的百分比是:1-25%-30%-20%-5%=20%,
则人数是200×20%=40(人).补全图形如下:
(3);
(4)“平均每天帮助父母干家务的时长不少于30分钟”的学生大约有3000×(25%+5%)=900(人).
一、单选题
1.市某视力健康管理中心对全市初中生的视力情况进行了一次抽样调查,如图是利用调查所得数据绘制的频数直方图,则这组数据的组数与组距分别是( )
A.4和0.20 B.4和0.30 C.5和0.20 D.5和0.30
2.为了检查近期期末复习的教学效果,某班数学老师把期末测评成绩进行了统计,得到如下的频数分布直方图.下列说法错误的是( )
A.成绩x在70≤x<80范围内的人数最多
B.数学老师按成绩范围分成了5组,组距是10
C.及格(60分以上)的人数有34人
D.全班一共有40人
3.在样本频数分布直方图中,有11个小长方形,若中间的小长方形的面积等于其他10个小长方形面积之和的,且中间一组的频数为40,则样本容量为( )
A.0.2 B.160 C.0.25 D.200
4.已知一组数据有80个,其中最大值为140,最小值为40,取组距为10,则可分成( ).
A.11组 B.9组 C.8组 D.10组
5.学校七年级学生做校服,校服分小号、中号、大号、特大号四种,随抽取若干名学生调查身高得如下统计分布表:
型号 身高x/cm 人数 频率
小号 145≤x<155 20 0.2
中号 155≤x<165 a 0.45
大号 165≤x<175 30 b
特大号 175≤x<185 5 0.05
求a= ,b= .( )
A.45 0.3 B.25 0.3 C.45 0.03 D.35 0.3
6.某班有48名同学,在一次数学检测中,分数均为整数,其成绩绘制成的频数直方图如图所示,从左到右的小长方形的高度比是1:3:6:4:2,则分数在70.5~80.5之间的人数是( )
A.12 B.16 C.24 D.18
7.为了了解某校七年级学生的体能情况,随机调查了其中100名学生,测试学生在1分钟内跳绳的次数,并绘制成如图所示的频数分布直方图.请根据图形计算,跳绳次数(x)在120≤x<200范围内人数占抽查学生总人数的百分比为( )
A.43% B.50% C.57% D.73%
8.数学老师将本班学生的身高数据(精确到1厘米)交给甲、乙两同学,要求他们各自绘制一幅频数分布直方图.经确认,甲绘制的图是正确的,乙在整理时漏了一个数据.由此可判断,下列说法错误的是( )
A.该班共有学生60人
B.乙在整理时遗漏的数据一定在169.5-173.5这个范围内
C.某同学身高155厘米,那么班上恰有10人比他矮
D.某同学身高165厘米,那么班上比他高的人数不超过全班人数的25%
9.某校组织学生参加安全知识竞赛,并抽取部分学生成绩绘制成如图所示的统计图(每组不包括最小值,包括最大值),图中从左至右前四组的百分比分别是,第五组的频数是8.下列判断正确的有( )
①第五组的百分比为16%;
②参加统计调查的竞赛学生共有100人;
③成绩在70-80分的人数最多;
④80分以上(不含80分)的学生有14名.
A.1个 B.2个 C.3个 D.4个
二、填空题
10.小强调查“每人每天的用水量”这一问题时,收集到60个数据,最大数据是64升,最小数据是45升,若取组距为4,则应分为_________组绘制频数分布表.
11.一个容量为的样本的最大值为,最小值,若取组距为,则应该分的组数为______.
12.一组数据经整理后分成五组,第一,二,三,四小组的频率分别为0.1,0.1,0.3,0.2,若第二小组的频数是6,则第五小组的频数是____.
13.超市为了制定某个时间段收银台开放方案,统计了这个时间段顾客在收银台排队付款的等待时间,并绘制成如下的频数分布直方图(图中等待时间1-2分钟表示大于或等于1分钟而小于2分钟,其它类同),这个时间段内顾客等待时间不少于5分钟的人数为________.
14.某校有名学生,随机抽查名学生的视力状况,其频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,则该校视力为及以上的学生约有_______人.
15.某中学七年级甲、乙两个班参加了一次数学考试,每班的考试人数都为40人,每个班的考试成绩分为A、B、C、D、E五个等级,现将两个班数学考试成绩统计如下:
根据以上统计图提供的信息,可知两个班人数相等的等级是__________.
16.秋季新学期开学,某中学对初一新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格.现随机抽取了部分学生的成绩制作成如下表格,则_____,__.
分数段 频数 频率
6
20 0.4
15
0.18
三、解答题
17.下面是2023年全国一些省(自治区、直辖市)的城市园林绿地面积(单位:).
北京 61595 上海 116929 湖北 54884 云南 22372
天津 17369 江苏 214989 湖南 42940 西藏 2174
河北 60923 浙江 74362 广东 401604 陕西 23426
山西 27973 安徽 67269 广西5 57812 甘肃 14702
内蒙古 29585 福建 41330 海南 48947 青海 3290
辽宁 84145 江西 37596 重庆 32451 宁夏 14525
吉林 34755 山东 146993 四川 66817 新疆 36359
黑龙江 64234 河南 62947 贵州 27771
根据上面提供的数据分析2023年这些地区的城市园林绿地面积的分布情况图.
18.某市在实施居民用水定额管理前,对居民生活用水情况进行了调查下表是通过简单随机抽样调查获得的50个家庭去年的月均用水量(单位:)
4.7 2.0 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.0 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 8.3 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
(1)请选择合适的组距和组数,列出样本频数分布表,画出频数分布直方图.从直方图中你能得到什么信息?
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使60%的家庭水费支出不受影响,你觉得家庭月均用水量应该定为多少?为什么?
19.某校组织了一次“疫情防控知识”专题网上学习,并进行了一次全校名学生都参加的网上测试.阅卷后,教务处随机抽取份答卷进行分析统计,绘制了频数分布表和频数分布直方图(不完整),请结合图表信息回答下列问题:
成绩(分) 频数(人) 频率
合计
(Ⅰ)_______,_______,_______,频率分布表的组距是_______;
(Ⅱ)补全频数分布直方图;
(Ⅲ)全校学生参加网上测试,成绩在范围内的学生约有多少人?
20.某学校在本学期开展数学拓展活动,为了解开展数学拓展活动后学生不同阶段的学习效果,决定随机抽取七年级部分学生进行两次跟踪测评(两次随机抽取的学生人数相同),第一次是开展数学拓展活动初期的学习质量测评,第二次是开展数学拓展活动个月后的学习质量测评.根据测评的数学成绩制作了第一次测评的数学成绩频数分布直方图(如图,每一组包括左边端点,不包括右边端点)和第二次测评的数学成绩频数分布表(如表).
第二次测评的数学成绩频数分布表:
成绩
频数
根据以上图表信息,完成下列问题:
第一次测评的数学成绩频数分布直方图
(1)______;
(2)若分及以上为优秀.
①开展数学拓展活动个月后,请估计该校名七年级学生数学成绩优秀的人数;
②请分别计算两次测评数学成绩的优秀率,并对开展数学拓展活动的效果进行分析.
21.体育老师统计了全班同学60秒跳绳的次数,并列出下面的频数分布表:
次数 60≤x<80 80≤x<100 100≤x<120 120≤x<140 140≤x<160 160≤x<180
频数 4 13 19 7 5 2
请你结合表中所给信息解答下列问题:
(1)全班有 名学生;
(2)组距是 ,组数是 ;
(3)跳绳次数x在100≤x<140范国的学生占全班学生的 %;
(4)请把频数分布直方图补充完整.
22.某学校在暑假期间安排了“心怀感恩 孝敬父母”的实践活动,倡导学生在假期中多帮父母干家务.开学以后,校学生会的老师们在学校随机抽取了部分学生,就暑假期间“平均每天帮助父母干家务所用时长”进行了调查,以下是根据相关数据绘制的统计图的一部分(每段时长均含最小值,不含最大值):
根据上述信息,回答下列问题:
(1)在本次随机抽取的样本中,调查的学生人数是 人;
(2)补全扇形统计图,补全频数分布直方图;
(3)在扇形统计图中,计算出“10 ~ 20分钟”部分所对应的圆心角的度数;
(4)如果该校共有学生3000人,请你估计“平均每天帮助父母干家务的时长不少于30分钟”的学生大约有多少人?
答案
一、单选题
1.D
【解析】解:观察图形可得:有五组数据,因此组数为5;
组距=4.253.95=0.30
故答案选D
2.C
【解析】解:A、成绩x在70≤x<80范围内有14人,人数最多,说法正确;
B、数学老师按成绩范围分成了5组,组距是10,说法正确;
C、及格(60分以上)的人数有36人,说法错误;
D、全班一共有40人,说法正确.
故选:C.
3.D
【解析】
解:所有长方形的面积和为1,又因为中间小长方形的面积是其余10个小长方形面积之和的,所以中间的面积为,
即频率为0.20,且中间一组的频数为40,所以样本容量为200,
故选:D.
4.A
【解析】解:由组数=(最大值-最小值)÷组距可得:
组数=(140-40)÷10+1=11,
故选择:A
5.A
【解析】
观察统计表知:小组的频数20,频率0.2,
∴学生总数为20÷0.2=100(人);∴,
∴,
故选:A.
6.D
【解析】
解:分数在70.5到80.5之间的人数是:×48=18(人);
故选:D.
7.C
【解析】解:总人数为10+33+40+17=100人,
120≤x<200范围内人数为40+17=57人,
在120≤x<200范围内人数占抽查学生总人数的百分比为=57%
故选:C.
8.B
【解析】
解:根据甲绘制的统计图,可知该班共有学生10+15+20+10+5=60(人),故A正确,不符合题意;
根据甲绘制的统计图,可知该班身高小于154.5的学生有10人,故C正确,不符合题意;
根据甲绘制的统计图,可知该班身高大于或等于165的学生有15人,,故D正确,不符合题意;
根据甲的直方图能够得出身高在(169.5﹣174.5)cm之间的人数为5人,从乙图中发现,身高在(169.5﹣173.5)cm的人数是4人,因此,乙在整理时遗漏的数据一定在169.5-174.5这个范围内,故B错误,符合题意;
故选B.
9.B
【解析】
解:由1-4%-12%-40%-28%=16%可知①正确;
由可知参加统计调查的竞赛学生共有50人,∴②错误;
由频数分布直方图可以得知成绩在70-80分的人数最多,∴③正确;
由可知80分以上(不含80分)的学生有22名,④错误;
故选B.
二、填空题
10.5
【解析】
解:应分(64-45)÷4=4.75,
∵第一组的下限应低于最小变量值,最后一组的上限应高于最大变量值,
∴应分5组.
故本题答案为:5.
11.7
【解析】
解:这个样本的最大值与最小值的差为,
∵组距为4,且,
∴应该分的组数为7,
故答案为:7.
12.18
【解析】解:根据题意,得:
第五小组的频率是1-0.1-0.1-0.3-0.2=0.3
已知第二小组的频数是6,频率是0.1
则这组数据共有
第五小组的频数是:60×0.3=18
故答案为:18
13.16
【解析】解:由频数分布直方图可得,
这个时间段内顾客等待时间不少于5分钟的人数为:9+5+2=16,
故答案为:16.
14.400
【解析】解:由题意得:1000×=400(人),
即该校视力为4.9及以上的学生约有400人,
故答案为:400.
15.A
【解析】解:甲班各等级人数分别为:A等级:2人;B等级:5人;C等级:12人;D等级:13人;E等级:8人;
乙班各等级人数:A等级:40×5%=2人;
B等级:40×10%=4人;
C等级:40×35%=14人;
D、E等级:40×25%=10人;
所以两个班A等级的人数相等,
故答案为:A.
16.0.3 9
【解析】
抽取的学生总数是:(人,
;;
故答案为:0.3,9.
三、解答题
17.
解:首先计算最大值和最小值,在表中的数据中,最小值是2174,最大值是401604,它们的差是399430,说明城市园林绿地面积的变化范围是399430hm2.
根据上面的计算结果,把所有的数据进行分组.如果从最小值起每隔40000hm2作为一组,则,所以要将数据分成十组:
2174≤x<42174,42174≤x<82174,
82174≤x<122174,122174≤x<162174,
162174≤x<202174,202174≤x<242174,
242174≤x<282174,282174≤x<322174,
322174≤x<362174,362174≤x<402174.
列频数分布表:
画频数分布直方图:
由上表和直方图可以看出,2009年城市园林绿地面积大部分落在2174hm2至122174hm2之间,其他区域较少.其中绿地面积在2174hm2至42174hm2的城市最多,有15个,而绿地面积在242174hm2至401274hm2范围内的很少,只有1个城市.
根据上面的分析可以看出,2009年大部分城市的园林绿地面积都比较少,城市园林绿地面积的差距很大.从一个方面说明我国的城市园林绿地面积比较小,其中中型的城市园林绿地面积有待进一步加大.
18.
(1)选组距为1,组数为7.频数分布表为:
月均用水量 划记 频数 百分比
4 8%
正正丅 12 24%
正正 14 28%
正 9 18%
正一 6 12%
3 6%
丅 2 4%
合计 50 100%
频数分布直方图为:
从直方图中得到,月均用水量处于4至5t的最多,月均用水量处于8至9t的最少.
(2)标准定为.因为50个家庭的数据是通过简单随机抽样获得的,样本中家庭月均用水量不超过的占60%,由样本估计总体,可以推断约60%的家庭水费支出不受影响.
19.
(1)a=100×0.1=10,
b=100 10 18 35 12=25,
n=25÷100=0.25.
由图可得频率分布表的组距是10
故答案为:10,25,0.25,10;
(2)如图,即为补充完整的频数分布直方图
(3)成绩在范围内的学生约有2500×=1175(人).
20.
解:(1)由第一次测评的数学成绩频数分布直方图可知参与总人数为:
(人),
根据两次开展数学拓展活动的人数相同,
,
故答案是:;
(2)①根据第二次测评的数学成绩频数分布表,
可知分及以上人数为:(人),
优秀率为:,
该校名七年级学生数学成绩优秀的人数为:(人);
②根据第一次测评的数学成绩频数分布直方图,
可知分及以上人数为:(人),
优秀率为:,
由(2)①得第二次测评的数学成绩优秀率为:,
,
开展数学拓展活动对学生的学习质量有提升作用.
21.
解:(1)全班学生人数为:(人;
(2)组距是20,组数是6;
(3)跳绳次数在范围的学生占全班学生的百分比为,
故答案是:52;
(4)如图所示:
22.
解:(1)调查的学生人数是:40÷20%=200(人),
故答案是:200;
(2) 3040分钟50÷200×100%=25%;
40~50分钟的人数所占的百分比是10 ÷200×100%=5%,
则20~30分钟所占的百分比是:1-25%-30%-20%-5%=20%,
则人数是200×20%=40(人).补全图形如下:
(3);
(4)“平均每天帮助父母干家务的时长不少于30分钟”的学生大约有3000×(25%+5%)=900(人).
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
