小升初分班考必刷题(试题)数学六年级下册人教版(含解析)
文档属性
| 名称 | 小升初分班考必刷题(试题)数学六年级下册人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 474.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-01 22:11:15 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
绝密★启用前
小升初分班考必刷题(试题)数学六年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题
1.冰壶运动是冬奥会的一项重要比赛项目,运动员将冰壶向右平移至如图的位置,那么它平移了( )格。
A.5 B.6 C.7
2.康康和乐乐用1,2,3三张数字卡片玩游戏。每次任意摸两张卡片,若卡片上的数字之和是单数,则康康赢,若是双数,则乐乐赢。( )赢得可能性大。
A.康康 B.乐乐 C.无法确定
3.把500毫升的水倒入不同的正方体容器中,容器中水面的高度与容器的底面积( )。
A.成正比例关系 B.成反比例关系 C.不成比例
4.两个圆锥的底面积相等,第一个圆锥与第二个圆锥的高之比是5∶7,第一个圆锥的体积是35立方厘米,第二个圆锥的体积是( )立方厘米。
A.25 B.49 C.84
5.观察下图,学校在公园的( )。
A.北偏西50°方向400米处B.北偏东50°方向400米处 C.北偏西40°方向400米处
6.将一个圆按1∶n的比缩小,缩小后与缩小前图形的面积比是( )。
A.1∶n B.n2∶1 C.1∶n2
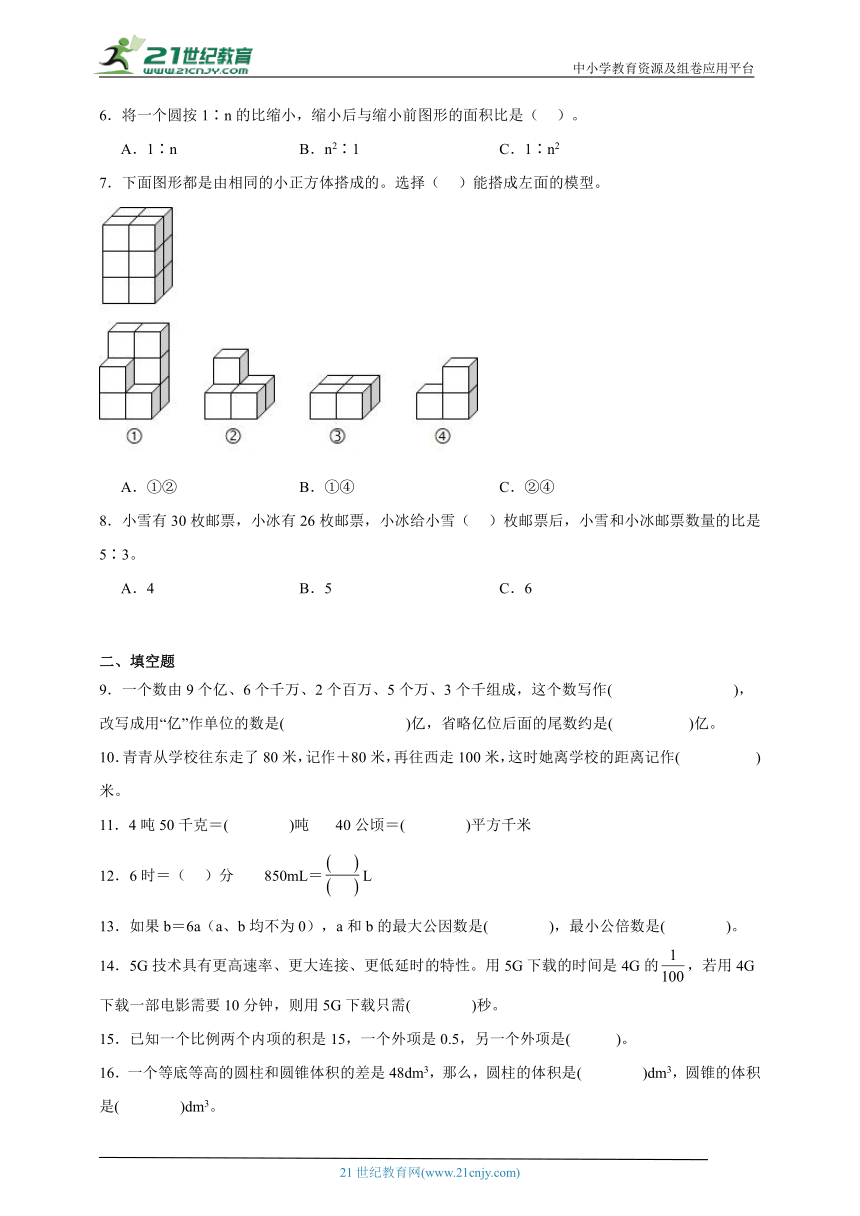
7.下面图形都是由相同的小正方体搭成的。选择( )能搭成左面的模型。
A.①② B.①④ C.②④
8.小雪有30枚邮票,小冰有26枚邮票,小冰给小雪( )枚邮票后,小雪和小冰邮票数量的比是5∶3。
A.4 B.5 C.6
二、填空题
9.一个数由9个亿、6个千万、2个百万、5个万、3个千组成,这个数写作( ),改写成用“亿”作单位的数是( )亿,省略亿位后面的尾数约是( )亿。
10.青青从学校往东走了80米,记作+80米,再往西走100米,这时她离学校的距离记作( )米。
11.4吨50千克=( )吨 40公顷=( )平方千米
12.6时=( )分 850mL=L
13.如果b=6a(a、b均不为0),a和b的最大公因数是( ),最小公倍数是( )。
14.5G技术具有更高速率、更大连接、更低延时的特性。用5G下载的时间是4G的,若用4G下载一部电影需要10分钟,则用5G下载只需( )秒。
15.已知一个比例两个内项的积是15,一个外项是0.5,另一个外项是( )。
16.一个等底等高的圆柱和圆锥体积的差是48dm3,那么,圆柱的体积是( )dm3,圆锥的体积是( )dm3。
三、判断题
17.a÷b=,那么a=9,b=4。( )
18.如图,阴影部分表示的算式是。( )
19.10克糖放入100克水中,糖占糖水的10%。( )
20.5∶9的后项若变成90,要使比值不变,前项应加45。( )
21.钟面上12:15的时候,时针和分针的较小夹角是直角。( )
四、计算题
22.直接写出得数。
(1) (2) (3) (4) (5)
(6) (7) (8) (9) (10)
23.选择合适的方法计算。
(1) (2)
(3) (4)
24.解下列方程。
(1)x+x= (2)x-4.8×=12
25.求阴影部分的面积。(单位:厘米)
五、解答题
26.张老师要用100元钱购买班级六一节礼物。他先花37.5元买了笔记本,并准备用剩下的钱买一些笔,每支笔2.5元。他可以买多少支同样的笔?
27.食堂运进一批大米,吃了这批大米的,还剩400千克。这批大米共多少千克?(先把线段图补充完整,再列方程解答)
28.学校修建一个圆柱形蓄水池,水池底面直径4米,高2米。
(1)蓄水池的容积是多少立方米?
(2)在蓄水池的底面和四周粉刷一层水泥,粉刷的面积是多少平方米?
29.乐乐家平均每月各种支出占家庭消费支出总额百分比情况如下图。
(1)结合扇形统计图,填写下表。
项目 购物支出 教育支出 其他支出 ……
费用(元) 2400 1200 ……
百分比(%) 20 15 ……
(2)根据以下信息解答。
恩格尔系数=食品支出总额÷家庭消费支出总额×100%。国际上常用恩格尔系数来衡量一个国家和地区人民生活水平的状况,如下表:
恩格尔系数 50%~60% 40%~50% 30%~40% 20%~30%
生活水平 温饱 小康 相对富裕 富裕
乐乐家平均每月食品支出总额为4200元,他家生活属于( )水平,请说明理由。
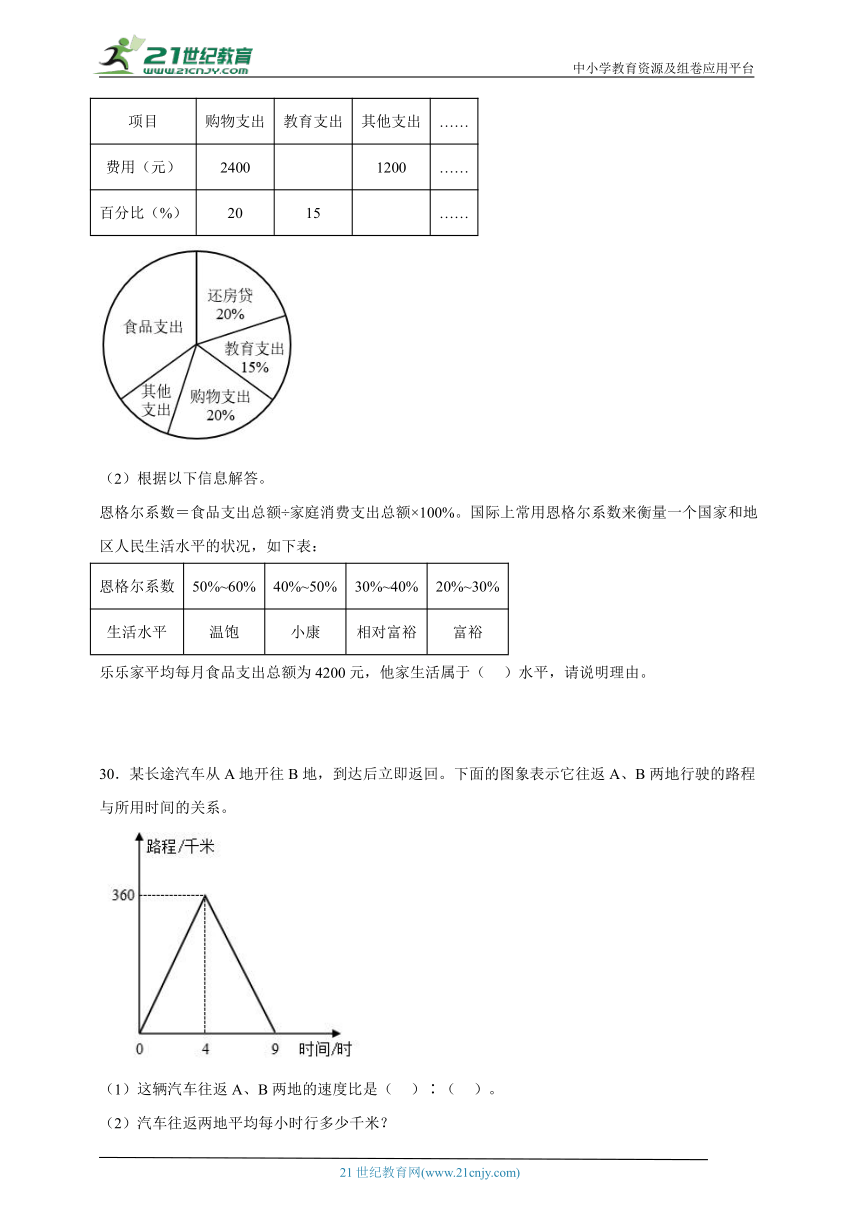
30.某长途汽车从A地开往B地,到达后立即返回。下面的图象表示它往返A、B两地行驶的路程与所用时间的关系。
(1)这辆汽车往返A、B两地的速度比是( )∶( )。
(2)汽车往返两地平均每小时行多少千米?
(3)C地在A、B两地之间。汽车从去时经过C地,到从B地返回时再次经过C地,共用时。A、C两地相距多少千米?
参考答案:
1.B
【分析】由题数出对应点平移了多少格即可知道整个图形平移了多少格。
【详解】冰壶运动是冬奥会的一项重要比赛项目,运动员将冰壶向右平移至如图的位置,那么它平移了6格。
故答案为:B
【点睛】此题主要考查平移的意义以及在实际当中的运用。
2.A
【分析】三张卡片,任意摸两张,有3种情况,即1+2=3;1+3=4;2+3=5;再根据它们的和是双数多,还剩单数多;进行分析解答。
【详解】1+2=3,和为单数;
1+3=4,和为双数;
2+3=,和为单数;
3和5都是单数,有2个;4是双数;有1个
2>1,康康赢得可能性大。
故答案为:A
【点睛】解答本题的关键是求出和是单数还剩双数,再根据可能性的大小进行解答。
3.B
【分析】两种相关联的量,如果它们的比值一定,则这两种量成正比例关系;如果它们的乘积一定,则这两种量成反比例关系。据此解答。
【详解】正方体的体积=底面积×高,据此可得:容器的底面积×水面的高度=500毫升。容器中水面的高度与容器的底面积的乘积一定,则这两种量成反比例关系。
故答案为:B
【点睛】本题考查正比例和反比例的辨认。熟练掌握正比例和反比例的意义是解题的关键。
4.B
【分析】圆锥的体积=Sh。两个圆锥的底面积相等,第一个圆锥与第二个圆锥的高之比是5∶7,则第一个圆锥与第二个圆锥的体积之比是5∶7,第二个圆锥的体积是第一个圆锥体积的。已知第一个圆锥的体积是35立方厘米,用35乘即可求出第二个圆锥的体积。
【详解】35×=49(立方厘米)
故答案为:B
【点睛】本题考查了圆锥的体积和比的综合应用。根据圆锥的体积公式,得出“第一个圆锥与第二个圆锥的体积之比是5∶7”是解题的关键。
5.C
【分析】根据地图上的方向,上北下南,左西右东,方向与距离是确定物体位置的两大要素,根据例题可得:图中的1条小线段的长度,代表实际距离100米,以公园位置为观测点,即可确定学校的方向。
【详解】由分析可得:图中的1条小线段的长度,代表实际距离100米,所以以公园位置为观测中心,学校在公园的北偏西40°方向400米处。
故答案为:C
【点睛】根据物体位置确定方向,关键是观测点的确定,同一物体,所选的观测点不同,方向也会改变。
6.C
【分析】根据题意,把缩小前圆的半径设为1,缩小后圆的半径为,再根据圆的面积公式:π×半径2,代入数据,求出缩小后圆的面积与缩小前圆的面积,再根据比的意义,用缩小后的面积∶缩小前的面积,即可解答。
【详解】设缩小前圆的半径为1,则缩小后圆的半径为。
缩小后圆的面积:π×()2
缩小前圆的面积:π×12=π
π×()2∶π
=(×n2)∶(1×n2)
=1∶n2
故答案为:C
【点睛】根据图形的缩小、圆的面积以及比的意义进行解答。
7.B
【分析】观察图形可知,这个几何体是由长2个、宽是2个、高是3个小正方体拼成;共有2×2×3=12个小正方体组成;由此逐项分析选项进行解答。
【详解】A.①和②;①是由9个小正方体搭成,②是5个小正方体搭成,9+5=14(个);①和②不能搭成;
B.①和④;①是9个小正方体搭成,④是3个小正方体搭成,9+2=12(个);①和④能搭成。
C.②和④;②是5个小正方体搭成,④是3个小正方体搭成,5+3=8(个);②和④不能搭成;
故答案为:B
【点睛】本题考查从不同方向观察物体和几何图,以及长方体的体积公式的应用。
8.B
【分析】无论小冰给小雪几枚邮票,两人的邮票总数不变。两人一共有30+26=56(枚)邮票,当小冰给小雪邮票后,小雪和小冰邮票数量的比是5∶3,这时小雪的邮票数占两人邮票总数的,用56乘即可求出小雪现在的邮票数量。最后用小雪现在的邮票数量减去原来的数量即可求出小冰给小雪几枚邮票。
【详解】30+26=56(枚)
56×=35(枚)
35-30=5(枚)
故答案为:B
【点睛】本题考查按比例分配问题。明确两人的邮票总数不变,根据两人邮票数量的比求出其中一人现在的邮票数量是解题的关键。
9. 962053000 9.62053 10
【分析】整数的写法:从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0;
改写成用“亿”作单位的数:在亿位的后边,点上小数点,去掉小数点末尾的0,并加上一个“亿”字;
省略“亿”后面的尾数,就是四舍五入法到亿位,把亿位后的千万位上的数进行四舍五入,再在数的后面加上“亿”字。
【详解】一个数由9个亿、6个千万、2个百万、5个万、3个千组成,这个数写作962053000;
962053000=9.62053亿
962053000≈10亿
【点睛】掌握整数的写法、整数的改写、整数的近似数求法是解题的关键。
10.-20
【分析】此题主要用正负数来表示具有意义相反的两种量:向东走记为正,则向西走就记为负,直接得出结论即可。
【详解】青青从学校往东走了80米,记作﹢80米,再往西走100米,这时她离学校的距离记作-20米。
【点睛】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
11. 4.05 0.4
【分析】低级单位换高级单位除以进率,根据1吨=1000千克,用50÷1000再加上4即可;根据1平方千米=100公顷,用40÷100即可。
【详解】4吨50千克=4吨+50÷1000吨=4吨+0.05吨=4.05吨
40公顷=40÷100平方千米=0.4平方千米
【点睛】熟练掌握质量单位、面积单位的换算,是解答此题的关键。
12.360;
【分析】高级单位换低级单位乘进率,根据1小时=60分,用6×60即可;低级单位换高级单位除以进率,根据1L=1000mL,用850÷1000即可。
【详解】6时=6×60分=360分
850mL=850÷1000L=L
【点睛】熟练掌握时间单位、容积单位的换算,是解答此题的关键。
13. a b
【分析】两个数是倍数关系时,最大公因数是较小数,最小公倍数是较大数。
【详解】如果b=6a(a、b均不为0),那么a、b是倍数关系,且b>a;
a和b的最大公因数是a,最小公倍数是b。
【点睛】掌握当两个数是倍数关系时,它们的最大公因数和最小公倍数的求法是解题的关键。
14.6
【分析】把用4G下载的时间看作单位“1”,根据分数乘法的意义,用10分钟乘,就是用5G下载需要的时间。
【详解】10分=600秒
600×=6(秒)
【点睛】此题是考查分数乘法的意义及应用。求一个数的几分之几是多少,用这个数乘分率。
15.30
【分析】根据比例的基本性质:在比例里,两个外项的积等于两个内项的积。已知一个比例两个内项的积是15,那么这个比例的两个外项的积也是15,用积除以其中一个外项,即可求出另一个外项。
【详解】15÷0.5=30
【点睛】掌握比例的基本性质及应用是解题的关键。
16. 24 72
【分析】根据“等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍”,也就是说,圆锥的体积是1份,圆柱的体积是3份,那么它们的体积就相差2份;已知它们的体积相差48dm3,用48除以2就是圆锥的体积,再用圆锥的体积乘3就是圆柱的体积。
【详解】48÷(3-1)
=48÷2
=24(dm3)
24×3=72(dm3)
【点睛】此题是考查体积的计算,可利用“等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍”来解答。
17.×
【分析】a÷b=,只能说明a和b的商是。比如a=18,b=8时,;再比如a=27,b=12时,。所以不能仅仅因为a÷b=,就确定a=9,b=4。据此解答。
【详解】由分析可知,a÷b=,那么a=9,b=4。该说法是错误的。
故答案为:×
18.√
【分析】把大长方形看作单位“1”,大长方形被平均分成2份,1份涂色,涂色部分占大长方形的;把涂色部分看作单位“1”,它又被平均分成3份,2份涂色,第二次涂色的部分占第一次涂色部分的,占整个图形的。
【详解】
表示的算式是。原题干说法正确。
故答案为:√
19.×
【分析】糖占糖水的百分率=糖的质量÷糖水的质量×100%,据此解答。
【详解】10÷(10+100)×100%
=10÷110×100%
=0.0909×100%
≈9%
所以原题计算错误。
故答案为:×
20.√
【分析】根据比的基本性质,比的前项和后项,同时乘或除以相同的数(0除外),比值不变,进行分析。
【详解】90÷9×5=50
50-5=45
5∶9的后项若变成90,要使比值不变,前项应加45,说法正确。
故答案为:√
21.×
【分析】钟面上12:15时,时针在12和1之间,而分针指着3,时针和分针的夹角小于90°,是个锐角。
【详解】钟面上12:15的时候,时针和分针的较小夹角是锐角,不是直角。
故答案为:×
22.(1);(2);(3)1.5;(4);(5);
(6);(7);(8);(9);(10)
【详解】略
23.(1)99;(2)999000;
(3);(4)720
【分析】(1)按照运算顺序计算即可,先算乘除,后算减法;
(2)先将333×666转换成999×222,再根据乘法分配律将999提出来进行简便计算;
(3)按照运算顺序计算即可,先算小括号里面的除法然后算减法,再算括号外面的乘法,最后算加法;
(4)先算小括号内的减法,再算中括号内的乘法,最后算除法。
【详解】(1)12×15-2835÷35
=180-81
=99
(2)333×666+999×778
=333×(3×222)+999×778
=333×3×222+999×778
=999×222+999×778
=999×(222+778)
=999×1000
=999000
(3)
=
=
=
=
=
=
(4)
=
=
=
=
=
=
=
24.(1)x=;(2)x=22
【分析】(1)首先化简方程,然后根据等式的性质,两边同时除以即可;
(2)首先根据等式的性质,两边同时加上4,然后两边再同时除以即可。
【详解】(1)x+x=
解:x=
x÷=÷
x×=×
x=
(2)x-4.8×=12
解:x-4=12
x-4+4=12+4
x=16
x÷=16÷
x×=16×
x=22
25.22.26平方厘米
【分析】观察图形,正方形左下角空白部分的面积=正方形的面积-圆的面积,阴影部分的面积=大三角形的面积-正方形左下角空白部分的面积;根据正方形的面积公式S=a2,圆的面积公式S=πr2,三角形的面积公式S=ah÷2,代入数据计算求解。
【详解】6×6-3.14×62×
=36-3.14×36×
=36-28.26
=7.74(平方厘米)
(6+4)×6÷2-7.74
=10×6÷2-7.74
=30-7.74
=22.26(平方厘米)
阴影部分的面积是22.26平方厘米。
26.25支
【分析】先求出买了笔记本后还剩下多少钱,然后根据总价÷单价=数量,据此求出笔的支数。
【详解】(100-37.5)÷2.5
=62.5÷2.5
=25(支)
答:他可以买25支同样的笔。
【点睛】本题考查单价、数量和总价,明确它们之间的关系是解题的关键。
27.1000千克,线段图见详解
【分析】把这批大米的重量看作单位“1”,吃了这批大米的,还剩下1-=,正好是400千克,根据部分的量÷所对应的分率=单位“1”的量,用除法解答即可。
【详解】如图:
400÷(1-)
=400÷
=1000(千克)
答:这批大米共1000千克。
【点睛】本题考查分数除法,明确部分的量÷所对应的分率=单位“1”的量是解题的关键。
28.(1)25.12立方米
(2)37.68平方米
【分析】(1)根据圆柱体积=底面积×高,即可求出蓄水池的容积。
(2)底面积+侧面积=粉刷水泥的面积,据此列式解答。
【详解】(1)3.14×(4÷2)2×2
=3.14×4×2
=25.12(立方米)
答:蓄水池的容积是25.12立方米。
(2)3.14×(4÷2)2+3.14×4×2
=3.14×4+25.12
=12.56+25.12
=37.68(平方米)
答:粉刷的面积是37.68平方米。
【点睛】关键是掌握并灵活运用圆柱表面积和体积公式。
29.(1)1800;10
(2)相对富裕;理由见详解
【分析】(1)将家庭消费支出总额看作单位“1”,购物支出÷对应百分率=家庭消费支出总额,家庭消费支出总额×教育支出对应百分率=教育支出;其他支出÷家庭消费支出总额=其他支出对应百分率,据此填表。
(2)将家庭消费支出总额看作单位“1”,1-所有已知和求出的项目对应百分率=食品支出对应百分率,家庭消费支出总额×食品支出对应百分率=食品支出,根据恩格尔系数=食品支出总额÷家庭消费支出总额×100%,求出乐乐家的恩格尔系数,找到对应生活水平即可。
【详解】(1)2400÷20%=12000(元)
12000×15%=1800(元)
1200÷12000=10%
项目 购物支出 教育支出 其他支出 ……
费用(元) 2400 1800 1200 ……
百分比(%) 20 15 10 ……
(2)12000×(1-20%-15%-10%-20%)
=12000×35%
=4200(元)
4200÷12000×100%=35%
在30%~40%之间,他家生活属于相对富裕水平。
【点睛】利用扇形统计图解决问题,就是解决有关不同类型的百分数应用题,按照百分数相关解题思路解答即可。
30.(1)5;4
(2)80千米
(3)198千米
【分析】(1)根据“路程÷时间=速度”,分别求出这辆汽车去时的速度、返回时的速度;再求去时的速度与返回时的速度之比,化简比即可;
(2)从图中可知,A、B两地的距离是360千米,那么往返两地的路程是(360×2)千米,往返的时间是9时,根据“往返的平均速度=往返路程÷往返时间”,代入数据计算即可。
(3)根据“路程=速度×时间”,先用返回时的速度乘从B地到C地的时间,求出B、C两地的距离;再用全程减去B、C两地的距离即是A、C两地的距离。
【详解】(1)去时的速度:360÷4=90(千米/时)
返回时的速度:
360÷(9-4)
=360÷5
=72(千米/时)
速度之比:
90∶72
=(90÷18)∶(72÷18)
=5∶4
这辆汽车往返A、B两地的速度比是5∶4。
(2)360×2÷9
=720÷9
=80(千米)
答:汽车往返两地平均每小时行80千米。
(3)B、C两地的距离:
72×
=72×
=162(千米)
A、C两地的距离:360-162=198(千米)
答:A、C两地相距198千米。
【点睛】掌握折线统计图的特点和作用,从中获取信息,解决有关的实际问题;灵活运用行程问题中的速度、时间、路程之间的关系是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
绝密★启用前
小升初分班考必刷题(试题)数学六年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题
1.冰壶运动是冬奥会的一项重要比赛项目,运动员将冰壶向右平移至如图的位置,那么它平移了( )格。
A.5 B.6 C.7
2.康康和乐乐用1,2,3三张数字卡片玩游戏。每次任意摸两张卡片,若卡片上的数字之和是单数,则康康赢,若是双数,则乐乐赢。( )赢得可能性大。
A.康康 B.乐乐 C.无法确定
3.把500毫升的水倒入不同的正方体容器中,容器中水面的高度与容器的底面积( )。
A.成正比例关系 B.成反比例关系 C.不成比例
4.两个圆锥的底面积相等,第一个圆锥与第二个圆锥的高之比是5∶7,第一个圆锥的体积是35立方厘米,第二个圆锥的体积是( )立方厘米。
A.25 B.49 C.84
5.观察下图,学校在公园的( )。
A.北偏西50°方向400米处B.北偏东50°方向400米处 C.北偏西40°方向400米处
6.将一个圆按1∶n的比缩小,缩小后与缩小前图形的面积比是( )。
A.1∶n B.n2∶1 C.1∶n2
7.下面图形都是由相同的小正方体搭成的。选择( )能搭成左面的模型。
A.①② B.①④ C.②④
8.小雪有30枚邮票,小冰有26枚邮票,小冰给小雪( )枚邮票后,小雪和小冰邮票数量的比是5∶3。
A.4 B.5 C.6
二、填空题
9.一个数由9个亿、6个千万、2个百万、5个万、3个千组成,这个数写作( ),改写成用“亿”作单位的数是( )亿,省略亿位后面的尾数约是( )亿。
10.青青从学校往东走了80米,记作+80米,再往西走100米,这时她离学校的距离记作( )米。
11.4吨50千克=( )吨 40公顷=( )平方千米
12.6时=( )分 850mL=L
13.如果b=6a(a、b均不为0),a和b的最大公因数是( ),最小公倍数是( )。
14.5G技术具有更高速率、更大连接、更低延时的特性。用5G下载的时间是4G的,若用4G下载一部电影需要10分钟,则用5G下载只需( )秒。
15.已知一个比例两个内项的积是15,一个外项是0.5,另一个外项是( )。
16.一个等底等高的圆柱和圆锥体积的差是48dm3,那么,圆柱的体积是( )dm3,圆锥的体积是( )dm3。
三、判断题
17.a÷b=,那么a=9,b=4。( )
18.如图,阴影部分表示的算式是。( )
19.10克糖放入100克水中,糖占糖水的10%。( )
20.5∶9的后项若变成90,要使比值不变,前项应加45。( )
21.钟面上12:15的时候,时针和分针的较小夹角是直角。( )
四、计算题
22.直接写出得数。
(1) (2) (3) (4) (5)
(6) (7) (8) (9) (10)
23.选择合适的方法计算。
(1) (2)
(3) (4)
24.解下列方程。
(1)x+x= (2)x-4.8×=12
25.求阴影部分的面积。(单位:厘米)
五、解答题
26.张老师要用100元钱购买班级六一节礼物。他先花37.5元买了笔记本,并准备用剩下的钱买一些笔,每支笔2.5元。他可以买多少支同样的笔?
27.食堂运进一批大米,吃了这批大米的,还剩400千克。这批大米共多少千克?(先把线段图补充完整,再列方程解答)
28.学校修建一个圆柱形蓄水池,水池底面直径4米,高2米。
(1)蓄水池的容积是多少立方米?
(2)在蓄水池的底面和四周粉刷一层水泥,粉刷的面积是多少平方米?
29.乐乐家平均每月各种支出占家庭消费支出总额百分比情况如下图。
(1)结合扇形统计图,填写下表。
项目 购物支出 教育支出 其他支出 ……
费用(元) 2400 1200 ……
百分比(%) 20 15 ……
(2)根据以下信息解答。
恩格尔系数=食品支出总额÷家庭消费支出总额×100%。国际上常用恩格尔系数来衡量一个国家和地区人民生活水平的状况,如下表:
恩格尔系数 50%~60% 40%~50% 30%~40% 20%~30%
生活水平 温饱 小康 相对富裕 富裕
乐乐家平均每月食品支出总额为4200元,他家生活属于( )水平,请说明理由。
30.某长途汽车从A地开往B地,到达后立即返回。下面的图象表示它往返A、B两地行驶的路程与所用时间的关系。
(1)这辆汽车往返A、B两地的速度比是( )∶( )。
(2)汽车往返两地平均每小时行多少千米?
(3)C地在A、B两地之间。汽车从去时经过C地,到从B地返回时再次经过C地,共用时。A、C两地相距多少千米?
参考答案:
1.B
【分析】由题数出对应点平移了多少格即可知道整个图形平移了多少格。
【详解】冰壶运动是冬奥会的一项重要比赛项目,运动员将冰壶向右平移至如图的位置,那么它平移了6格。
故答案为:B
【点睛】此题主要考查平移的意义以及在实际当中的运用。
2.A
【分析】三张卡片,任意摸两张,有3种情况,即1+2=3;1+3=4;2+3=5;再根据它们的和是双数多,还剩单数多;进行分析解答。
【详解】1+2=3,和为单数;
1+3=4,和为双数;
2+3=,和为单数;
3和5都是单数,有2个;4是双数;有1个
2>1,康康赢得可能性大。
故答案为:A
【点睛】解答本题的关键是求出和是单数还剩双数,再根据可能性的大小进行解答。
3.B
【分析】两种相关联的量,如果它们的比值一定,则这两种量成正比例关系;如果它们的乘积一定,则这两种量成反比例关系。据此解答。
【详解】正方体的体积=底面积×高,据此可得:容器的底面积×水面的高度=500毫升。容器中水面的高度与容器的底面积的乘积一定,则这两种量成反比例关系。
故答案为:B
【点睛】本题考查正比例和反比例的辨认。熟练掌握正比例和反比例的意义是解题的关键。
4.B
【分析】圆锥的体积=Sh。两个圆锥的底面积相等,第一个圆锥与第二个圆锥的高之比是5∶7,则第一个圆锥与第二个圆锥的体积之比是5∶7,第二个圆锥的体积是第一个圆锥体积的。已知第一个圆锥的体积是35立方厘米,用35乘即可求出第二个圆锥的体积。
【详解】35×=49(立方厘米)
故答案为:B
【点睛】本题考查了圆锥的体积和比的综合应用。根据圆锥的体积公式,得出“第一个圆锥与第二个圆锥的体积之比是5∶7”是解题的关键。
5.C
【分析】根据地图上的方向,上北下南,左西右东,方向与距离是确定物体位置的两大要素,根据例题可得:图中的1条小线段的长度,代表实际距离100米,以公园位置为观测点,即可确定学校的方向。
【详解】由分析可得:图中的1条小线段的长度,代表实际距离100米,所以以公园位置为观测中心,学校在公园的北偏西40°方向400米处。
故答案为:C
【点睛】根据物体位置确定方向,关键是观测点的确定,同一物体,所选的观测点不同,方向也会改变。
6.C
【分析】根据题意,把缩小前圆的半径设为1,缩小后圆的半径为,再根据圆的面积公式:π×半径2,代入数据,求出缩小后圆的面积与缩小前圆的面积,再根据比的意义,用缩小后的面积∶缩小前的面积,即可解答。
【详解】设缩小前圆的半径为1,则缩小后圆的半径为。
缩小后圆的面积:π×()2
缩小前圆的面积:π×12=π
π×()2∶π
=(×n2)∶(1×n2)
=1∶n2
故答案为:C
【点睛】根据图形的缩小、圆的面积以及比的意义进行解答。
7.B
【分析】观察图形可知,这个几何体是由长2个、宽是2个、高是3个小正方体拼成;共有2×2×3=12个小正方体组成;由此逐项分析选项进行解答。
【详解】A.①和②;①是由9个小正方体搭成,②是5个小正方体搭成,9+5=14(个);①和②不能搭成;
B.①和④;①是9个小正方体搭成,④是3个小正方体搭成,9+2=12(个);①和④能搭成。
C.②和④;②是5个小正方体搭成,④是3个小正方体搭成,5+3=8(个);②和④不能搭成;
故答案为:B
【点睛】本题考查从不同方向观察物体和几何图,以及长方体的体积公式的应用。
8.B
【分析】无论小冰给小雪几枚邮票,两人的邮票总数不变。两人一共有30+26=56(枚)邮票,当小冰给小雪邮票后,小雪和小冰邮票数量的比是5∶3,这时小雪的邮票数占两人邮票总数的,用56乘即可求出小雪现在的邮票数量。最后用小雪现在的邮票数量减去原来的数量即可求出小冰给小雪几枚邮票。
【详解】30+26=56(枚)
56×=35(枚)
35-30=5(枚)
故答案为:B
【点睛】本题考查按比例分配问题。明确两人的邮票总数不变,根据两人邮票数量的比求出其中一人现在的邮票数量是解题的关键。
9. 962053000 9.62053 10
【分析】整数的写法:从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0;
改写成用“亿”作单位的数:在亿位的后边,点上小数点,去掉小数点末尾的0,并加上一个“亿”字;
省略“亿”后面的尾数,就是四舍五入法到亿位,把亿位后的千万位上的数进行四舍五入,再在数的后面加上“亿”字。
【详解】一个数由9个亿、6个千万、2个百万、5个万、3个千组成,这个数写作962053000;
962053000=9.62053亿
962053000≈10亿
【点睛】掌握整数的写法、整数的改写、整数的近似数求法是解题的关键。
10.-20
【分析】此题主要用正负数来表示具有意义相反的两种量:向东走记为正,则向西走就记为负,直接得出结论即可。
【详解】青青从学校往东走了80米,记作﹢80米,再往西走100米,这时她离学校的距离记作-20米。
【点睛】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
11. 4.05 0.4
【分析】低级单位换高级单位除以进率,根据1吨=1000千克,用50÷1000再加上4即可;根据1平方千米=100公顷,用40÷100即可。
【详解】4吨50千克=4吨+50÷1000吨=4吨+0.05吨=4.05吨
40公顷=40÷100平方千米=0.4平方千米
【点睛】熟练掌握质量单位、面积单位的换算,是解答此题的关键。
12.360;
【分析】高级单位换低级单位乘进率,根据1小时=60分,用6×60即可;低级单位换高级单位除以进率,根据1L=1000mL,用850÷1000即可。
【详解】6时=6×60分=360分
850mL=850÷1000L=L
【点睛】熟练掌握时间单位、容积单位的换算,是解答此题的关键。
13. a b
【分析】两个数是倍数关系时,最大公因数是较小数,最小公倍数是较大数。
【详解】如果b=6a(a、b均不为0),那么a、b是倍数关系,且b>a;
a和b的最大公因数是a,最小公倍数是b。
【点睛】掌握当两个数是倍数关系时,它们的最大公因数和最小公倍数的求法是解题的关键。
14.6
【分析】把用4G下载的时间看作单位“1”,根据分数乘法的意义,用10分钟乘,就是用5G下载需要的时间。
【详解】10分=600秒
600×=6(秒)
【点睛】此题是考查分数乘法的意义及应用。求一个数的几分之几是多少,用这个数乘分率。
15.30
【分析】根据比例的基本性质:在比例里,两个外项的积等于两个内项的积。已知一个比例两个内项的积是15,那么这个比例的两个外项的积也是15,用积除以其中一个外项,即可求出另一个外项。
【详解】15÷0.5=30
【点睛】掌握比例的基本性质及应用是解题的关键。
16. 24 72
【分析】根据“等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍”,也就是说,圆锥的体积是1份,圆柱的体积是3份,那么它们的体积就相差2份;已知它们的体积相差48dm3,用48除以2就是圆锥的体积,再用圆锥的体积乘3就是圆柱的体积。
【详解】48÷(3-1)
=48÷2
=24(dm3)
24×3=72(dm3)
【点睛】此题是考查体积的计算,可利用“等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍”来解答。
17.×
【分析】a÷b=,只能说明a和b的商是。比如a=18,b=8时,;再比如a=27,b=12时,。所以不能仅仅因为a÷b=,就确定a=9,b=4。据此解答。
【详解】由分析可知,a÷b=,那么a=9,b=4。该说法是错误的。
故答案为:×
18.√
【分析】把大长方形看作单位“1”,大长方形被平均分成2份,1份涂色,涂色部分占大长方形的;把涂色部分看作单位“1”,它又被平均分成3份,2份涂色,第二次涂色的部分占第一次涂色部分的,占整个图形的。
【详解】
表示的算式是。原题干说法正确。
故答案为:√
19.×
【分析】糖占糖水的百分率=糖的质量÷糖水的质量×100%,据此解答。
【详解】10÷(10+100)×100%
=10÷110×100%
=0.0909×100%
≈9%
所以原题计算错误。
故答案为:×
20.√
【分析】根据比的基本性质,比的前项和后项,同时乘或除以相同的数(0除外),比值不变,进行分析。
【详解】90÷9×5=50
50-5=45
5∶9的后项若变成90,要使比值不变,前项应加45,说法正确。
故答案为:√
21.×
【分析】钟面上12:15时,时针在12和1之间,而分针指着3,时针和分针的夹角小于90°,是个锐角。
【详解】钟面上12:15的时候,时针和分针的较小夹角是锐角,不是直角。
故答案为:×
22.(1);(2);(3)1.5;(4);(5);
(6);(7);(8);(9);(10)
【详解】略
23.(1)99;(2)999000;
(3);(4)720
【分析】(1)按照运算顺序计算即可,先算乘除,后算减法;
(2)先将333×666转换成999×222,再根据乘法分配律将999提出来进行简便计算;
(3)按照运算顺序计算即可,先算小括号里面的除法然后算减法,再算括号外面的乘法,最后算加法;
(4)先算小括号内的减法,再算中括号内的乘法,最后算除法。
【详解】(1)12×15-2835÷35
=180-81
=99
(2)333×666+999×778
=333×(3×222)+999×778
=333×3×222+999×778
=999×222+999×778
=999×(222+778)
=999×1000
=999000
(3)
=
=
=
=
=
=
(4)
=
=
=
=
=
=
=
24.(1)x=;(2)x=22
【分析】(1)首先化简方程,然后根据等式的性质,两边同时除以即可;
(2)首先根据等式的性质,两边同时加上4,然后两边再同时除以即可。
【详解】(1)x+x=
解:x=
x÷=÷
x×=×
x=
(2)x-4.8×=12
解:x-4=12
x-4+4=12+4
x=16
x÷=16÷
x×=16×
x=22
25.22.26平方厘米
【分析】观察图形,正方形左下角空白部分的面积=正方形的面积-圆的面积,阴影部分的面积=大三角形的面积-正方形左下角空白部分的面积;根据正方形的面积公式S=a2,圆的面积公式S=πr2,三角形的面积公式S=ah÷2,代入数据计算求解。
【详解】6×6-3.14×62×
=36-3.14×36×
=36-28.26
=7.74(平方厘米)
(6+4)×6÷2-7.74
=10×6÷2-7.74
=30-7.74
=22.26(平方厘米)
阴影部分的面积是22.26平方厘米。
26.25支
【分析】先求出买了笔记本后还剩下多少钱,然后根据总价÷单价=数量,据此求出笔的支数。
【详解】(100-37.5)÷2.5
=62.5÷2.5
=25(支)
答:他可以买25支同样的笔。
【点睛】本题考查单价、数量和总价,明确它们之间的关系是解题的关键。
27.1000千克,线段图见详解
【分析】把这批大米的重量看作单位“1”,吃了这批大米的,还剩下1-=,正好是400千克,根据部分的量÷所对应的分率=单位“1”的量,用除法解答即可。
【详解】如图:
400÷(1-)
=400÷
=1000(千克)
答:这批大米共1000千克。
【点睛】本题考查分数除法,明确部分的量÷所对应的分率=单位“1”的量是解题的关键。
28.(1)25.12立方米
(2)37.68平方米
【分析】(1)根据圆柱体积=底面积×高,即可求出蓄水池的容积。
(2)底面积+侧面积=粉刷水泥的面积,据此列式解答。
【详解】(1)3.14×(4÷2)2×2
=3.14×4×2
=25.12(立方米)
答:蓄水池的容积是25.12立方米。
(2)3.14×(4÷2)2+3.14×4×2
=3.14×4+25.12
=12.56+25.12
=37.68(平方米)
答:粉刷的面积是37.68平方米。
【点睛】关键是掌握并灵活运用圆柱表面积和体积公式。
29.(1)1800;10
(2)相对富裕;理由见详解
【分析】(1)将家庭消费支出总额看作单位“1”,购物支出÷对应百分率=家庭消费支出总额,家庭消费支出总额×教育支出对应百分率=教育支出;其他支出÷家庭消费支出总额=其他支出对应百分率,据此填表。
(2)将家庭消费支出总额看作单位“1”,1-所有已知和求出的项目对应百分率=食品支出对应百分率,家庭消费支出总额×食品支出对应百分率=食品支出,根据恩格尔系数=食品支出总额÷家庭消费支出总额×100%,求出乐乐家的恩格尔系数,找到对应生活水平即可。
【详解】(1)2400÷20%=12000(元)
12000×15%=1800(元)
1200÷12000=10%
项目 购物支出 教育支出 其他支出 ……
费用(元) 2400 1800 1200 ……
百分比(%) 20 15 10 ……
(2)12000×(1-20%-15%-10%-20%)
=12000×35%
=4200(元)
4200÷12000×100%=35%
在30%~40%之间,他家生活属于相对富裕水平。
【点睛】利用扇形统计图解决问题,就是解决有关不同类型的百分数应用题,按照百分数相关解题思路解答即可。
30.(1)5;4
(2)80千米
(3)198千米
【分析】(1)根据“路程÷时间=速度”,分别求出这辆汽车去时的速度、返回时的速度;再求去时的速度与返回时的速度之比,化简比即可;
(2)从图中可知,A、B两地的距离是360千米,那么往返两地的路程是(360×2)千米,往返的时间是9时,根据“往返的平均速度=往返路程÷往返时间”,代入数据计算即可。
(3)根据“路程=速度×时间”,先用返回时的速度乘从B地到C地的时间,求出B、C两地的距离;再用全程减去B、C两地的距离即是A、C两地的距离。
【详解】(1)去时的速度:360÷4=90(千米/时)
返回时的速度:
360÷(9-4)
=360÷5
=72(千米/时)
速度之比:
90∶72
=(90÷18)∶(72÷18)
=5∶4
这辆汽车往返A、B两地的速度比是5∶4。
(2)360×2÷9
=720÷9
=80(千米)
答:汽车往返两地平均每小时行80千米。
(3)B、C两地的距离:
72×
=72×
=162(千米)
A、C两地的距离:360-162=198(千米)
答:A、C两地相距198千米。
【点睛】掌握折线统计图的特点和作用,从中获取信息,解决有关的实际问题;灵活运用行程问题中的速度、时间、路程之间的关系是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
