国庆长假八年级数学辅导第11章 全等三角形的判定
文档属性
| 名称 | 国庆长假八年级数学辅导第11章 全等三角形的判定 |

|
|
| 格式 | rar | ||
| 文件大小 | 83.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-09-29 00:00:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第11章 全等三角形
(第二课时) 三角形全等的判定
本节主要通过画两个全等的三角形,引导学生发现问题:要求证两个三角形全等需要些什么条件,然后由学生动手操作发现求证两三角形全等的条件有:“边边边”、“边角边”、“角边角”、“角角边”以及两直角三角形全等的“斜边直角边”,接着进一步引导学生思考证明三角形全等的思路,帮助一些看到证明题就头痛的学生解决问。
一.三角形全等的判定
这是本节的重点知识,在【知识点击】、【典例引路】、【当堂检测】、【基础训练】中设置了相应的例题以提高解题能力。
二.易错点
因为证明三角形全等的条件较多,学生很容易把“边边角”也用来证明三角形全等,值得注意的是,这“边边角”并不是三角形全等的条件。
点击一: 边边边公理:三边对应相等的两个三角形全等,简写为“边边边”或“SSS”
点击二: 边角边公理:有两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”
点击三: 角边角公理:两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”
点击四: 角角边推论:两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”.
点击五: 直角三角形全等的条件还有“斜边直角边公理”:有斜边和一条直角边对应相等的两个直角三角形全等,简写成“斜边直角边”或“HL”.
点击六: 全等三角形的应用:证明线段或角相等,通常先观察要证明的线段或角分布在怎样的两个可能全等的三角形中,再分析这两个三角形全等已经有什么条件,还缺少什么条件,最后证出所缺条件。
点击七: 证明三角形全等的思路
由于证明三角形全等的方法较多,因此证明两个三角形全等的思路与其他证明题目的思路有所不同,它不是先想用什么方法去证,而是先分析条件,观察待证全等的两个三角形中,已经具备了哪些条件,然后以其为基础,观察其他需要的条件,最后证出需要的条件。
例如:易得两边对应相等,则应再找,在(1)(2)中证出一个条件,则可以证出三角形的全等。
类型之一:SSS
已知:如图,点B、E、C、F在同一直线上,AB=DE、AC=DF、BE=CF。求证:△ABC≌△DEF。
【解析】已知中给的条件均为线段,由此可以考虑从边边边公理证明,这里又需用到等量公理。
【答案】
证明:
∵BE=CF
∴BE+EC=EC+CF(等量加等量和相等)
∴在△ABC和△DEF中
∴△ABC≌△DEF(SSS)
类型之二:ASA
已知:如图,∠1=∠2,∠ABC=∠DCB。求证:AB=DC。
【解析】证明线段或角相等时,常归结到线段或角所在的三角形的全等上,这是三角形全等判断的一种应用。本例要证明AB=DC,以它们所在的三角形全等为证明的手段,就是这种应用的一个例子。
要证AB=DC,只需证明△ABC≌DCB。
【答案】
证明:∵∠1= ∠2,∠ABC= ∠DCB,
∴∠ABC-∠1=∠DCB-∠2
∴∠DBC= ∠ACB
在△ABC和△DCB中:
∴△ABC ≌△DCB(ASA)
∴AB=DC
类型之三:AAS
已知:在△ABC中,AD为BC边上的中线,CE⊥AD,BF⊥AD。
求证:CE=BF
【解析】将CE与BF放在△CED与△BFD中,证明这两个三角形全等,问题便可解决,而
全等条件经过已知的转化是可以得到的。
【答案】
证明:
∵CE⊥AD,BF⊥AD
∴∠CED=∠BFD=90°(垂直定义)
∵D为BC中点
∴BD=DC(线段中点定义)
∴在△DEC与△DFB中
∴△DEC≌△DFB(AAS)
∴CE=BF(全等三角形对应边相等)
类型之四:综合
已知:如图,AB=DE,BC=EF,CD=FA,∠A= ∠D。求证:∠B= ∠E。
【解析】要证∠B=∠E,通常的思路是要证△ABC ≌△DEF,但如果连结AC、DE就会破坏∠A=∠D的条件。因此应当另想他法。观察后不难发现:△ABF≌△DEC,于是可证∠ABF= ∠DEC,进一步即可证明∠ABC= ∠DEF
【答案】
证明:连结BF、CF、CE
在△ABF和△DEC中
∴△ABF ≌△DEC(SAS)
∴∠1= ∠2,BF=EC
在△BFC和△ECF中
∴△BFC ≌△ECF(SSS)
∴∠3= ∠4
∴∠1+∠3= ∠2+∠4,即:∠ABC= ∠DEF
说明:如果直接证明线段或角相等比较困难时,可以将线段、角扩大(或缩小)或将线段、角分解为几部分,再分别证明扩大(或缩小)的量相等;或证明被分成的几部分对应相等,这是证明线段、角相等的一个常用手段。
1.如图两根长度相同的绳子,一端系在旗杆上,另一端分别固定在地面的木桩上,两个木桩离旗杆底部的距离相等吗?说明你的理由.?
【解析】审好题目相当于做对这道题的一半!所以,实际应用的题目一定要仔细审清题目,找出各个量之间的关系.
本题关键是要将实际生活的语言说明转化为数学上的各个量的关系.“由长度相同的绳子”可知AB=AC,而要求的是木桩B、C与O之间的距离关系,即求证BO=CO.有了明确的已知、求证,剩下的就是纯粹的全等证明了.
【答案】相等.?
证明:∵由题意AO⊥BC ∴∠AOB=∠AOC=90°?
∴Rt△AOB≌Rt△AOC(HL) ∴BO=CO
2.已知:如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,求证:BE⊥AC。
【解析】本题考察“HL”公理的应用。要证BE⊥AC,可证∠C+∠1=90°,而∠2+∠1=90°,只需证∠2=∠C。从而转化为证明它们所在的△BDF与△ADC全等,而这由“HL”公理不难得证。
【答案】
证明:∵AD⊥BC
∴∠BDA=∠ADC=90°
∴∠1+∠2=90°
在Rt△BDF和Rt△ADC中
∴Rt△BDF≌Rt△ADC(HL)
∴∠2=∠C
∴∠1+∠C=90°
∴∠BEC=90°
∴BE⊥AC
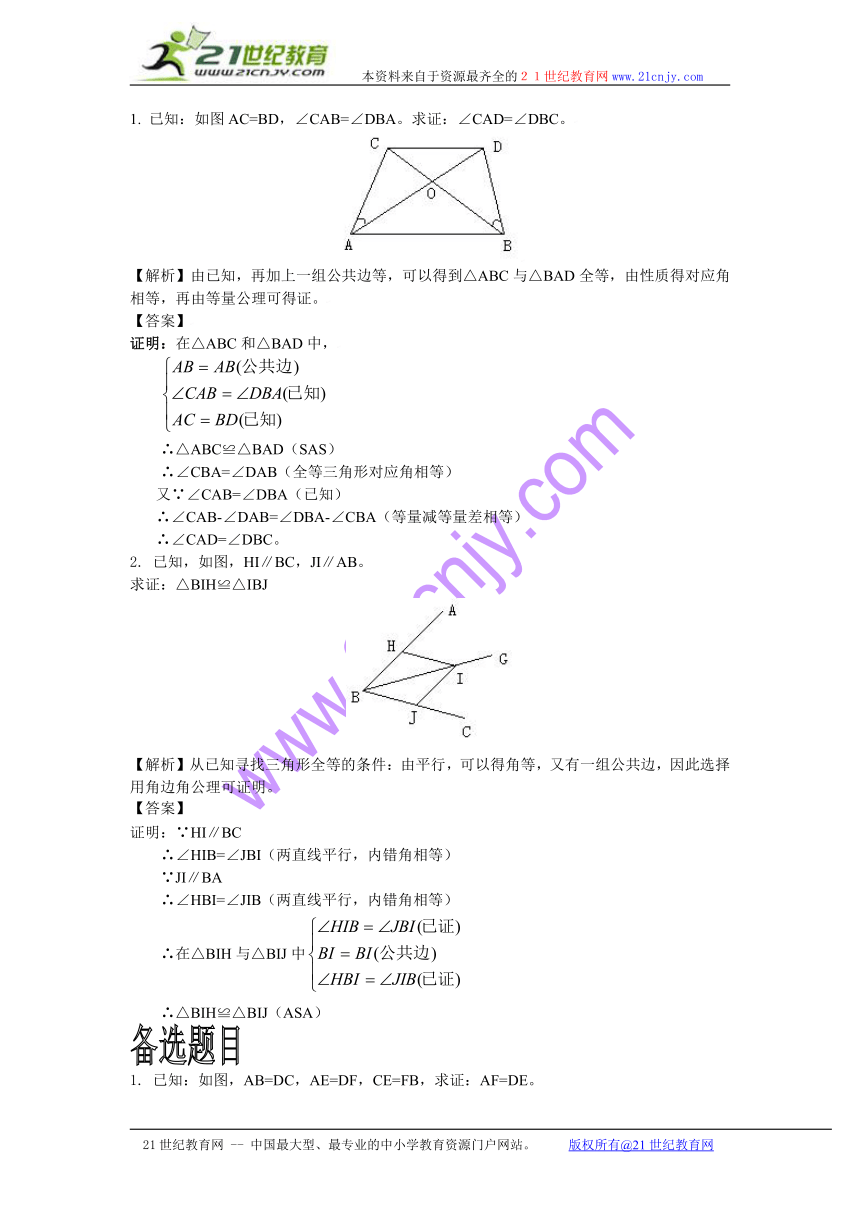
1. 已知:如图AC=BD,∠CAB=∠DBA。求证:∠CAD=∠DBC。
【解析】由已知,再加上一组公共边等,可以得到△ABC与△BAD全等,由性质得对应角相等,再由等量公理可得证。
【答案】
证明:在△ABC和△BAD中,
∴△ABC≌△BAD(SAS)
∴∠CBA=∠DAB(全等三角形对应角相等)
又∵∠CAB=∠DBA(已知)
∴∠CAB-∠DAB=∠DBA-∠CBA(等量减等量差相等)
∴∠CAD=∠DBC。
2. 已知,如图,HI∥BC,JI∥AB。
求证:△BIH≌△IBJ
【解析】从已知寻找三角形全等的条件:由平行,可以得角等,又有一组公共边,因此选择用角边角公理可证明。
【答案】
证明:∵HI∥BC
∴∠HIB=∠JBI(两直线平行,内错角相等)
∵JI∥BA
∴∠HBI=∠JIB(两直线平行,内错角相等)
∴在△BIH与△BIJ中
∴△BIH≌△BIJ(ASA)
1. 已知:如图,AB=DC,AE=DF,CE=FB,求证:AF=DE。
【解析】要证AF=DE,可证△AFB与△DEC全等,但还缺少相关角相等的条件,所以先证△AEB与△DFC全等。
【答案】
证明:∵CE=FB
∴CE+EF=FB+EF,即:CF=BE
在△AEB和△DFC中:
∴△AEB ≌△DFC(SSS)
∴∠B= ∠C
在△AFB和△DEC中:
∴△AFB ≌△DEC(SAS)
∴AF=DE
说明:本例是一个通过两次全等才能得到结论的题目,第一次全等的证明为第二次全等的证明创造必要的条件。
2. 已知:如图,△ABC中,D是BC的中点,∠1=∠2,求证:AB=AC。
【解析】此题看起来简单,其实不然。题中虽然有三个条件(∠1= ∠2;BD=CD,AD=AD),但无法证明△ABD ≌ACD。因此一定要找到别的角相等才能证明这两个三角形全等,于是要利用角平分线来构造两个全等的三角形。
【答案】
证明:作DE⊥AB于E,DF⊥AC于F
∵∠1= ∠2,DE⊥AB于E,DF⊥AC于F
∴DE=DF(角平分线上的点到角的两边的距离相等)
∵D是BC的中点
∴BD=CD
∵DE⊥AB于E,DF⊥AC于F
∴∠BED=90°,∠CFD=90°
在Rt△BDE和Rt△CDF中
∴Rt△BDE≌Rt△CDF(HL)
∴BE=CF
同理可证AE=AF
∴AE+BE=AF+CF即AB=AC
课时作业:
A等级
1、指出下图中的全等三角形各有几对,分别是哪些三角形。
△ABC中,AB=AC,D为BC中点,DE⊥AB,DF⊥AC
2、指出下图中的全等三角形各有几对,分别是哪些三角形。
OA=OB,OC=OD
3、指出下图中的全等三角形各有几对,分别是哪些三角形。
△ABC中,AB=AC,AE=AF,AD⊥BC于D
4、判断
( )1.三个角对应相等的两个三角形全等.
( )2.顶角及腰上的高相等的两个等腰三角形全等.
( )3.全等三角形对应的中线相等.
( )4.有一边相等的两个等腰直角三角形全等.
5、△ABC和△A′B′C′中,已知∠A=∠B′,AB=B′C′,增加条件 可使△ABC≌△B′C′A′(ASA).
6、△ABC中∠C=90°,BC>AC,E在BC上,且BE=EA. ∠CAE∶∠B=4∶7,则∠CEA=_____.
7、△ABC中,∠C=90°,BE为角平分线,ED⊥AB于D,若AE+ED=5cm,则AC=_______.
8、四边形ABCD中,边AB=DC,AD=BC,∠B=40°,则∠C= .
9、△ABC中,AB=AC,两中线BE,CF交于O,则按条件所作图形中共有 对全等三角形.
10、如图,AC⊥BE,AC=CE,CB=CF,把△EFC绕点C逆时针旋转90°,E落在______点上,F落在 点上.
B等级
11、判断
( )1.全等三角形的对应角相等,反之也成立.
( )2.周长为16,一边长为5的两个等腰三角形全等.
( )3.有两个角及一条边相等的两个三角形全等.
( )4.有锐角及斜边对应相等的两个直角三角形全等.
12、BP为∠ABC平分线,D在BP上,PA⊥BA于A,PC⊥BC于C,若∠ADP=35°,则∠BDC= 。
13、若△ABC≌△A′B′C′,且AB=10cm,BC=6cm,则A′C′的取值范围为 .
14、在△ABC和△DEF中,∠C=∠D,∠B=∠E,要使两三角形全等,需增加条件( )
A.AB=ED B.AB=FD C,AC=FD D. ∠A=∠F
15、下列条件能判断△ABC≌△DEF的是( )
A. ∠A=∠D, ∠C=∠F, ∠B=∠E B. ∠A=∠D,AB+AC=DE+DF
B. ∠A=∠D, ∠B=∠E,AC=DF D. ∠A=∠D,AC=DF,BC=EF
16、△ABC中,∠C=90°,AD为角平分线,BC=32,BD∶DC=9∶7,则点D到AB的距离为( )
A.18cm B.16cm C.14cm D.12cm
17、∠MON的边OM上有两点A、C,ON上有两点B、D,且OA=OB,OC=OD,AD,BC交于E,则①△OAD≌△OBC,②△ACE≌△BDE,③连OE.则OE平分∠AOB,以上结论( )
A.只有一个正确 B.只有一个不正确
C.都正确 D.都不正确
18、△ABC中,∠C=90°,AC=BC,AD为角平分线,DE⊥AB于E,且AB=6cm,则△DEB的周长为( )
A.4cm B.6cm C.8cm D.10cm
19、B为AC上一点,在AC同侧作等边△EAB及等边△DBC,那么下列式子错误的是( )
A.△ABD≌△EBC B. ∠BDA=∠BCE
C.△ABE≌△BCD
D.若BE交AD于M,CE交BD于N,那么△NBC≌△MBD
20、线段OD=DC,A在OC上,B在OD上,且OA=OB,OC=OD,∠COD=60°,∠C=,AC,BC交于E,则∠BED的度数是( )
A. 60° B.70° C.80° D.50°
C等级
21、已知:△ABC中,D、E、F分别是AB、AC、BC上的点,连结DE、EF,∠ADE=∠EFC,∠AED=∠ACB,DE=FC。
求证:△ADE≌△EFC
22、已知:△ABC是等边三角形,∠GAB=∠HBC=∠DCA,∠GBA=∠HCB=∠DAC。
求证:△ABG≌△BCH≌△CAD。
23、已知:如图∠1=∠2,∠3=∠4,求证:△ABC≌△ABD。
24、已知:AB=CD,AB∥DC
求证:△ABC≌△CDA
25、已知:DA⊥AB,CA⊥AE,AB=AE,AC=AD
求证:DE=BC
26、已知:△ABC中,AB=AC,D、E分别为AB、AC的中点
求证:∠ABE=∠ACD
27、已知:如图AC=BD,∠CAB=∠DBA。
求证:∠CAD=∠DBC。
28、如图,AB=CD,AE⊥BC,DF⊥BC,垂足分别为E,F,CE=BF.求证:AB∥CD.
29、如图,AE⊥BC,DF⊥BC,E,F是垂足,且AE=DF,AB=DC,求证:∠ABC=∠DCB.
30、我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等,那么在什么情况下,它们会全等?
⑴阅读与证明:
对于这两个三角形均为直角三角形,显然它们全等。
对于这两个三角形均为钝角三角形,可证明它们全等(证明略)
对于这两个三角形均为锐角三角形,它们也全等,可证明如下:
已知:△ABC、△均为锐角三角形,AB=,BC=,∠C=∠.证明:△ABC≌⊿.(请你将下列证明过程补充完整)
证明:分别过点B、,作BD⊥CA于D,⊥于,
则∠BDC=∠=90 .
∵BC=,∠C=∠.
∴△BCD≌△,∴BD=.
⑵归纳与叙述:由⑴可得到一个正确结论,请你写出这个结论.
A等级答案
1.3对,△ADE≌△ADF,△DBE≌△DCF,△BDA≌△CDA
2.3对,△OEC≌△OED,△ECA≌△EDB,△OEA≌△OEB
3.3对,△ABD≌△ACD,△AED≌△AFD,△ABE≌△ACF
4.1.)× 2.)√ 3.)√ 4.)×
5.∠B=∠C′
6.70°
7.5cm
8.140°
9.3
10.A、B
B等级答案
11.1.)× 2.)× 3.)× 4.)√
12.7.145°
13.4<A′C′<16
14.C
15.C
16.C
17.C
18.B
19.C
20.B
C等级答案
21.在△ADE与△EFC中
∴△ADE≌△EFC(ASA)
22.∵△ABC是等边三角形
∴AB=BC=CA
在△ABG与△BCH中
∴△ABG≌△BCH(ASA)
同理可证:△BCH≌△CAD
∴△ABG≌△BCH≌△CAD
23.∵∠ABC与∠3互补,∠ABD与∠4互补,又∠3=∠4,
∴∠ABC=∠ABD
在△ABC与△ABD中
∴△ABC≌△ABD(ASA)
24.∵AB∥CD
∴∠1=∠2
在△ABC与△CDA中
∴△ABC≌△CDA(SAS)
25.∵DA⊥AB,CA⊥AE
∴∠DAB=∠EAC
∴∠CAB=∠DAE
∴在△CAB与△EAD中
∴△CAB≌△EAD(SAS)
∴DE=BC
26.∵AB=AC
D、E分别为AB、AC中点
∴AD=AE
∴在△ADC与△AEB中
∴△ADC≌△AEB(SAS)
∴∠ABE=∠ACD
27.证明:在△ABC和△BAD中,
∴△ABC≌△BAD(SAS)
∴∠CBA=∠DAB(全等三角形对应角相等)
又∵∠CAB=∠DBA(已知)
∴∠CAB-∠DAB=∠DBA-∠CBA(等量减等量差相等)
∴∠CAD=∠DBC。
28.因为CE=BF,所以CE+EF=BF+EF,即BE=CF,
在Rt△AEB和Rt△DCF中,
所以△ABE≌△DCF,
所以∠B=∠C,
所以AB∥CD.
29.因为AE⊥BC,DF⊥BC,
所以在Rt△ABE和Rt△DCF中,
所以Rt△ABE≌Rt△DCF,
所以∠ABC=∠DCB.
30.⑴又∵AB=A1B1,∠ADB=∠A1D1B1=90°,
∴△ADB≌△A1D1B1 ,∠A=∠A1,
又∵∠C=∠C1,BC=B1C1,
∴△ABC≌△A1B1C1。
⑵若△ABC与△A1B1C1均为锐角三角形或均为直角三角形或均为钝角三角形,AB=A1B1,BC=B1Cl,∠C=∠Cl.则△ABC≌△A1B1C1.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第11章 全等三角形
(第二课时) 三角形全等的判定
本节主要通过画两个全等的三角形,引导学生发现问题:要求证两个三角形全等需要些什么条件,然后由学生动手操作发现求证两三角形全等的条件有:“边边边”、“边角边”、“角边角”、“角角边”以及两直角三角形全等的“斜边直角边”,接着进一步引导学生思考证明三角形全等的思路,帮助一些看到证明题就头痛的学生解决问。
一.三角形全等的判定
这是本节的重点知识,在【知识点击】、【典例引路】、【当堂检测】、【基础训练】中设置了相应的例题以提高解题能力。
二.易错点
因为证明三角形全等的条件较多,学生很容易把“边边角”也用来证明三角形全等,值得注意的是,这“边边角”并不是三角形全等的条件。
点击一: 边边边公理:三边对应相等的两个三角形全等,简写为“边边边”或“SSS”
点击二: 边角边公理:有两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”
点击三: 角边角公理:两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”
点击四: 角角边推论:两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”.
点击五: 直角三角形全等的条件还有“斜边直角边公理”:有斜边和一条直角边对应相等的两个直角三角形全等,简写成“斜边直角边”或“HL”.
点击六: 全等三角形的应用:证明线段或角相等,通常先观察要证明的线段或角分布在怎样的两个可能全等的三角形中,再分析这两个三角形全等已经有什么条件,还缺少什么条件,最后证出所缺条件。
点击七: 证明三角形全等的思路
由于证明三角形全等的方法较多,因此证明两个三角形全等的思路与其他证明题目的思路有所不同,它不是先想用什么方法去证,而是先分析条件,观察待证全等的两个三角形中,已经具备了哪些条件,然后以其为基础,观察其他需要的条件,最后证出需要的条件。
例如:易得两边对应相等,则应再找,在(1)(2)中证出一个条件,则可以证出三角形的全等。
类型之一:SSS
已知:如图,点B、E、C、F在同一直线上,AB=DE、AC=DF、BE=CF。求证:△ABC≌△DEF。
【解析】已知中给的条件均为线段,由此可以考虑从边边边公理证明,这里又需用到等量公理。
【答案】
证明:
∵BE=CF
∴BE+EC=EC+CF(等量加等量和相等)
∴在△ABC和△DEF中
∴△ABC≌△DEF(SSS)
类型之二:ASA
已知:如图,∠1=∠2,∠ABC=∠DCB。求证:AB=DC。
【解析】证明线段或角相等时,常归结到线段或角所在的三角形的全等上,这是三角形全等判断的一种应用。本例要证明AB=DC,以它们所在的三角形全等为证明的手段,就是这种应用的一个例子。
要证AB=DC,只需证明△ABC≌DCB。
【答案】
证明:∵∠1= ∠2,∠ABC= ∠DCB,
∴∠ABC-∠1=∠DCB-∠2
∴∠DBC= ∠ACB
在△ABC和△DCB中:
∴△ABC ≌△DCB(ASA)
∴AB=DC
类型之三:AAS
已知:在△ABC中,AD为BC边上的中线,CE⊥AD,BF⊥AD。
求证:CE=BF
【解析】将CE与BF放在△CED与△BFD中,证明这两个三角形全等,问题便可解决,而
全等条件经过已知的转化是可以得到的。
【答案】
证明:
∵CE⊥AD,BF⊥AD
∴∠CED=∠BFD=90°(垂直定义)
∵D为BC中点
∴BD=DC(线段中点定义)
∴在△DEC与△DFB中
∴△DEC≌△DFB(AAS)
∴CE=BF(全等三角形对应边相等)
类型之四:综合
已知:如图,AB=DE,BC=EF,CD=FA,∠A= ∠D。求证:∠B= ∠E。
【解析】要证∠B=∠E,通常的思路是要证△ABC ≌△DEF,但如果连结AC、DE就会破坏∠A=∠D的条件。因此应当另想他法。观察后不难发现:△ABF≌△DEC,于是可证∠ABF= ∠DEC,进一步即可证明∠ABC= ∠DEF
【答案】
证明:连结BF、CF、CE
在△ABF和△DEC中
∴△ABF ≌△DEC(SAS)
∴∠1= ∠2,BF=EC
在△BFC和△ECF中
∴△BFC ≌△ECF(SSS)
∴∠3= ∠4
∴∠1+∠3= ∠2+∠4,即:∠ABC= ∠DEF
说明:如果直接证明线段或角相等比较困难时,可以将线段、角扩大(或缩小)或将线段、角分解为几部分,再分别证明扩大(或缩小)的量相等;或证明被分成的几部分对应相等,这是证明线段、角相等的一个常用手段。
1.如图两根长度相同的绳子,一端系在旗杆上,另一端分别固定在地面的木桩上,两个木桩离旗杆底部的距离相等吗?说明你的理由.?
【解析】审好题目相当于做对这道题的一半!所以,实际应用的题目一定要仔细审清题目,找出各个量之间的关系.
本题关键是要将实际生活的语言说明转化为数学上的各个量的关系.“由长度相同的绳子”可知AB=AC,而要求的是木桩B、C与O之间的距离关系,即求证BO=CO.有了明确的已知、求证,剩下的就是纯粹的全等证明了.
【答案】相等.?
证明:∵由题意AO⊥BC ∴∠AOB=∠AOC=90°?
∴Rt△AOB≌Rt△AOC(HL) ∴BO=CO
2.已知:如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,求证:BE⊥AC。
【解析】本题考察“HL”公理的应用。要证BE⊥AC,可证∠C+∠1=90°,而∠2+∠1=90°,只需证∠2=∠C。从而转化为证明它们所在的△BDF与△ADC全等,而这由“HL”公理不难得证。
【答案】
证明:∵AD⊥BC
∴∠BDA=∠ADC=90°
∴∠1+∠2=90°
在Rt△BDF和Rt△ADC中
∴Rt△BDF≌Rt△ADC(HL)
∴∠2=∠C
∴∠1+∠C=90°
∴∠BEC=90°
∴BE⊥AC
1. 已知:如图AC=BD,∠CAB=∠DBA。求证:∠CAD=∠DBC。
【解析】由已知,再加上一组公共边等,可以得到△ABC与△BAD全等,由性质得对应角相等,再由等量公理可得证。
【答案】
证明:在△ABC和△BAD中,
∴△ABC≌△BAD(SAS)
∴∠CBA=∠DAB(全等三角形对应角相等)
又∵∠CAB=∠DBA(已知)
∴∠CAB-∠DAB=∠DBA-∠CBA(等量减等量差相等)
∴∠CAD=∠DBC。
2. 已知,如图,HI∥BC,JI∥AB。
求证:△BIH≌△IBJ
【解析】从已知寻找三角形全等的条件:由平行,可以得角等,又有一组公共边,因此选择用角边角公理可证明。
【答案】
证明:∵HI∥BC
∴∠HIB=∠JBI(两直线平行,内错角相等)
∵JI∥BA
∴∠HBI=∠JIB(两直线平行,内错角相等)
∴在△BIH与△BIJ中
∴△BIH≌△BIJ(ASA)
1. 已知:如图,AB=DC,AE=DF,CE=FB,求证:AF=DE。
【解析】要证AF=DE,可证△AFB与△DEC全等,但还缺少相关角相等的条件,所以先证△AEB与△DFC全等。
【答案】
证明:∵CE=FB
∴CE+EF=FB+EF,即:CF=BE
在△AEB和△DFC中:
∴△AEB ≌△DFC(SSS)
∴∠B= ∠C
在△AFB和△DEC中:
∴△AFB ≌△DEC(SAS)
∴AF=DE
说明:本例是一个通过两次全等才能得到结论的题目,第一次全等的证明为第二次全等的证明创造必要的条件。
2. 已知:如图,△ABC中,D是BC的中点,∠1=∠2,求证:AB=AC。
【解析】此题看起来简单,其实不然。题中虽然有三个条件(∠1= ∠2;BD=CD,AD=AD),但无法证明△ABD ≌ACD。因此一定要找到别的角相等才能证明这两个三角形全等,于是要利用角平分线来构造两个全等的三角形。
【答案】
证明:作DE⊥AB于E,DF⊥AC于F
∵∠1= ∠2,DE⊥AB于E,DF⊥AC于F
∴DE=DF(角平分线上的点到角的两边的距离相等)
∵D是BC的中点
∴BD=CD
∵DE⊥AB于E,DF⊥AC于F
∴∠BED=90°,∠CFD=90°
在Rt△BDE和Rt△CDF中
∴Rt△BDE≌Rt△CDF(HL)
∴BE=CF
同理可证AE=AF
∴AE+BE=AF+CF即AB=AC
课时作业:
A等级
1、指出下图中的全等三角形各有几对,分别是哪些三角形。
△ABC中,AB=AC,D为BC中点,DE⊥AB,DF⊥AC
2、指出下图中的全等三角形各有几对,分别是哪些三角形。
OA=OB,OC=OD
3、指出下图中的全等三角形各有几对,分别是哪些三角形。
△ABC中,AB=AC,AE=AF,AD⊥BC于D
4、判断
( )1.三个角对应相等的两个三角形全等.
( )2.顶角及腰上的高相等的两个等腰三角形全等.
( )3.全等三角形对应的中线相等.
( )4.有一边相等的两个等腰直角三角形全等.
5、△ABC和△A′B′C′中,已知∠A=∠B′,AB=B′C′,增加条件 可使△ABC≌△B′C′A′(ASA).
6、△ABC中∠C=90°,BC>AC,E在BC上,且BE=EA. ∠CAE∶∠B=4∶7,则∠CEA=_____.
7、△ABC中,∠C=90°,BE为角平分线,ED⊥AB于D,若AE+ED=5cm,则AC=_______.
8、四边形ABCD中,边AB=DC,AD=BC,∠B=40°,则∠C= .
9、△ABC中,AB=AC,两中线BE,CF交于O,则按条件所作图形中共有 对全等三角形.
10、如图,AC⊥BE,AC=CE,CB=CF,把△EFC绕点C逆时针旋转90°,E落在______点上,F落在 点上.
B等级
11、判断
( )1.全等三角形的对应角相等,反之也成立.
( )2.周长为16,一边长为5的两个等腰三角形全等.
( )3.有两个角及一条边相等的两个三角形全等.
( )4.有锐角及斜边对应相等的两个直角三角形全等.
12、BP为∠ABC平分线,D在BP上,PA⊥BA于A,PC⊥BC于C,若∠ADP=35°,则∠BDC= 。
13、若△ABC≌△A′B′C′,且AB=10cm,BC=6cm,则A′C′的取值范围为 .
14、在△ABC和△DEF中,∠C=∠D,∠B=∠E,要使两三角形全等,需增加条件( )
A.AB=ED B.AB=FD C,AC=FD D. ∠A=∠F
15、下列条件能判断△ABC≌△DEF的是( )
A. ∠A=∠D, ∠C=∠F, ∠B=∠E B. ∠A=∠D,AB+AC=DE+DF
B. ∠A=∠D, ∠B=∠E,AC=DF D. ∠A=∠D,AC=DF,BC=EF
16、△ABC中,∠C=90°,AD为角平分线,BC=32,BD∶DC=9∶7,则点D到AB的距离为( )
A.18cm B.16cm C.14cm D.12cm
17、∠MON的边OM上有两点A、C,ON上有两点B、D,且OA=OB,OC=OD,AD,BC交于E,则①△OAD≌△OBC,②△ACE≌△BDE,③连OE.则OE平分∠AOB,以上结论( )
A.只有一个正确 B.只有一个不正确
C.都正确 D.都不正确
18、△ABC中,∠C=90°,AC=BC,AD为角平分线,DE⊥AB于E,且AB=6cm,则△DEB的周长为( )
A.4cm B.6cm C.8cm D.10cm
19、B为AC上一点,在AC同侧作等边△EAB及等边△DBC,那么下列式子错误的是( )
A.△ABD≌△EBC B. ∠BDA=∠BCE
C.△ABE≌△BCD
D.若BE交AD于M,CE交BD于N,那么△NBC≌△MBD
20、线段OD=DC,A在OC上,B在OD上,且OA=OB,OC=OD,∠COD=60°,∠C=,AC,BC交于E,则∠BED的度数是( )
A. 60° B.70° C.80° D.50°
C等级
21、已知:△ABC中,D、E、F分别是AB、AC、BC上的点,连结DE、EF,∠ADE=∠EFC,∠AED=∠ACB,DE=FC。
求证:△ADE≌△EFC
22、已知:△ABC是等边三角形,∠GAB=∠HBC=∠DCA,∠GBA=∠HCB=∠DAC。
求证:△ABG≌△BCH≌△CAD。
23、已知:如图∠1=∠2,∠3=∠4,求证:△ABC≌△ABD。
24、已知:AB=CD,AB∥DC
求证:△ABC≌△CDA
25、已知:DA⊥AB,CA⊥AE,AB=AE,AC=AD
求证:DE=BC
26、已知:△ABC中,AB=AC,D、E分别为AB、AC的中点
求证:∠ABE=∠ACD
27、已知:如图AC=BD,∠CAB=∠DBA。
求证:∠CAD=∠DBC。
28、如图,AB=CD,AE⊥BC,DF⊥BC,垂足分别为E,F,CE=BF.求证:AB∥CD.
29、如图,AE⊥BC,DF⊥BC,E,F是垂足,且AE=DF,AB=DC,求证:∠ABC=∠DCB.
30、我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等,那么在什么情况下,它们会全等?
⑴阅读与证明:
对于这两个三角形均为直角三角形,显然它们全等。
对于这两个三角形均为钝角三角形,可证明它们全等(证明略)
对于这两个三角形均为锐角三角形,它们也全等,可证明如下:
已知:△ABC、△均为锐角三角形,AB=,BC=,∠C=∠.证明:△ABC≌⊿.(请你将下列证明过程补充完整)
证明:分别过点B、,作BD⊥CA于D,⊥于,
则∠BDC=∠=90 .
∵BC=,∠C=∠.
∴△BCD≌△,∴BD=.
⑵归纳与叙述:由⑴可得到一个正确结论,请你写出这个结论.
A等级答案
1.3对,△ADE≌△ADF,△DBE≌△DCF,△BDA≌△CDA
2.3对,△OEC≌△OED,△ECA≌△EDB,△OEA≌△OEB
3.3对,△ABD≌△ACD,△AED≌△AFD,△ABE≌△ACF
4.1.)× 2.)√ 3.)√ 4.)×
5.∠B=∠C′
6.70°
7.5cm
8.140°
9.3
10.A、B
B等级答案
11.1.)× 2.)× 3.)× 4.)√
12.7.145°
13.4<A′C′<16
14.C
15.C
16.C
17.C
18.B
19.C
20.B
C等级答案
21.在△ADE与△EFC中
∴△ADE≌△EFC(ASA)
22.∵△ABC是等边三角形
∴AB=BC=CA
在△ABG与△BCH中
∴△ABG≌△BCH(ASA)
同理可证:△BCH≌△CAD
∴△ABG≌△BCH≌△CAD
23.∵∠ABC与∠3互补,∠ABD与∠4互补,又∠3=∠4,
∴∠ABC=∠ABD
在△ABC与△ABD中
∴△ABC≌△ABD(ASA)
24.∵AB∥CD
∴∠1=∠2
在△ABC与△CDA中
∴△ABC≌△CDA(SAS)
25.∵DA⊥AB,CA⊥AE
∴∠DAB=∠EAC
∴∠CAB=∠DAE
∴在△CAB与△EAD中
∴△CAB≌△EAD(SAS)
∴DE=BC
26.∵AB=AC
D、E分别为AB、AC中点
∴AD=AE
∴在△ADC与△AEB中
∴△ADC≌△AEB(SAS)
∴∠ABE=∠ACD
27.证明:在△ABC和△BAD中,
∴△ABC≌△BAD(SAS)
∴∠CBA=∠DAB(全等三角形对应角相等)
又∵∠CAB=∠DBA(已知)
∴∠CAB-∠DAB=∠DBA-∠CBA(等量减等量差相等)
∴∠CAD=∠DBC。
28.因为CE=BF,所以CE+EF=BF+EF,即BE=CF,
在Rt△AEB和Rt△DCF中,
所以△ABE≌△DCF,
所以∠B=∠C,
所以AB∥CD.
29.因为AE⊥BC,DF⊥BC,
所以在Rt△ABE和Rt△DCF中,
所以Rt△ABE≌Rt△DCF,
所以∠ABC=∠DCB.
30.⑴又∵AB=A1B1,∠ADB=∠A1D1B1=90°,
∴△ADB≌△A1D1B1 ,∠A=∠A1,
又∵∠C=∠C1,BC=B1C1,
∴△ABC≌△A1B1C1。
⑵若△ABC与△A1B1C1均为锐角三角形或均为直角三角形或均为钝角三角形,AB=A1B1,BC=B1Cl,∠C=∠Cl.则△ABC≌△A1B1C1.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
