国庆长假八年级数学辅导第11章角平分线的性质
文档属性
| 名称 | 国庆长假八年级数学辅导第11章角平分线的性质 |

|
|
| 格式 | rar | ||
| 文件大小 | 75.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-09-29 00:00:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第11章 全等三角形
(第三课时) 角的平分线的性质
本节主要通过介绍画角的平分线,引导学生发现问题:角的平分线有什么性质?通过将一个角对折的方法学习对角线的性质:在角的平分线上的点到这个角的两边的距离相等.利用三角形全等来说明角平分线的判定定理:到一个角的两边的距离相等的点在这个角的平分线上.接着引导学生试做一个三角形内的三个内角的角平分线,看看有什么特点,特点是:三角形的三条角平分线交于三角形内一点,并且这个点到三角形三边的距离相等.角的平分线的性质一课占有很重要的地位,它是证明线段相等、角相等的有利工具。
一.角的平分线的性质
这是本节的重点知识,但在以后的习题中很少会单独的出现只考查角平分线的性质的题目,一般会综合的考查三角形全等、平行线等有关知识,故在【知识点击】、【典例引路】、【当堂检测】、【基础训练】中设置了相应的例题以提高解题能力。
二.性质运用
在【备选题目】中,设置了角平分线与方程解决问题的题目,以提高学生的综合解题能力。
三.易错点
本节知识的易错点是,把角平分线的性质及角平分线的判断混淆了,所以在【典例引路】例3题及【基础训练】第3题设置了相应的题目。
点击一: 角平分线性质定理:在角的平分线上的点到这个角的两边的距离相等.
如图:AB是∠CAD的平分线,则有:CB=BD。
点击二: 角平分线判定定理:到一个角的两边的距离相等的点在这个角的平分线上.
如图:如果有CB=BD ,则有AB是∠CAD的平分线。
点击三: 三角形的三条角平分线交于三角形内一点,并且这个点到三角形三边的距离相等.
如图:在三角形ABC中,AD是∠BAC,BE是∠ABC的角平分线,则有IH=IG=IF。
类型之一:求证角平分线的性质定理
例1:三角形的三条角平分线交于一点,你知道这是为什么吗?
【解析】我们知道两条直线是交于一点的,因此可以想办法证明第三条角平分线通过前两条角平分线的交点.
【答案】已知:如图,△ABC的角平分线AD与BE交于点I,求证:点I在∠ACB的平分线上.
证明:过点I作IH⊥AB、IG⊥AC、IF⊥BC,垂足分别是点H、G、F.
∵点I在∠BAC的角平分线AD上,且IH⊥AB、IG⊥AC
∴IH=IG(角平分线上的点到角的两边距离相等)
同理 IH=IF ∴IG=IF(等量代换)
又IG⊥AC、IF⊥BC
∴点I在∠ACB的平分线上(到一个角的两边的距离相等的点,在这个角的平分线上)
即:三角形的三条角平分线交于一点.
类型之二:利用角平分线的性质求线段之比
例2:如图,已知:∠BAC=30,G为∠BAC的平分线上的一点,若EG ∥AC交AB于E,GD ⊥AC 于D,GD:GE=( )
【解析】作GF⊥AB于F(目的是为了用定理)
∵AG平分∠BAC,GD ⊥AC
∴ GF=GD(角平分线的性质定理)
∵ EG ∥AC ,∠BAC=300
∴∠FEG=300
∴FG:EG=1:2
∴GD:GE=1:2
【答案】1:2
类型之三: 利用角平分线的性质求角的度数
例3:在△ABC中,∠ABC=100,∠ACB=20,CE 平分∠ACB交 AB于 E,D在 AC上,且∠CBD=20。求∠CED的度数。
【解析】此题是考查利用角平分线的性质求角的度数。
【答案】作EF⊥ AC,延长CB,作EG ⊥CB
EH⊥ BD
∵CE平分∠ACB,∠ACB=200,
∴∠BCE=∠DCE=100,
∵∠CBD=200
∴ ∠ BDA=40 0
∵∠ABC=1000, ∠CBD=200
∴ ∠ABG=800,∠ABD=800
∴ ∠ABG=∠ABD
∴EH=EG
可证△BEH≌△ BEG(AAS)
∵CE平分∠ACB,
∴EF=EG(角平分线性质定理)
∴EF=EH
∴DE平分 ∠BDA(角平分线的判定定理)
∴∠EDA=200
∵∠EDA=∠ECA+∠CED
∴∠CED=200 -100=100
1. 如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C.下列结论错误的是( ).
A.AD=CP B.△ABP≌△CBP
C.△ABD≌△CBD D.∠ADB=∠CDB.
【解析】通过角平分线上的性质的运用推得△ABP≌△CBP ,△ABD≌△CBD ,∠ADB=∠CDB三项成立,A项不成立,能推出AD=DC,也能推得AP=PC。
【答案】A
2. 如图所示,AD⊥OB,BC⊥OA,垂足分别为D、C,AD与BC相交于点P,若PA=PB,则∠1与∠2的大小是()
A.∠1=∠2 B.∠1>∠2
C.∠1<∠2 D.无法确定
【解析】∵AD⊥OB,BC⊥OA,PA=PB,由角平分线的判定可知∠1=∠2.
【答案】A
3.△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=12cm,则△DBE的周长为()
A、12cm B、10cm C、14cm D、11cm
【解析】∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,易得△ACD≌△AED,
∴CD=DE,AE=AC,∴△DBE的周长=DE+EB+DE=CD+DB+EB=BC+EB=AC+EB=AE+EB=AB=12cm.
【答案】A
1. 已知AD是△ABC的角平分线,DE⊥AB于E,且DE=5cm,则点D到AC的距离是_____.
【解析】角平分线上的一点到角的两边距离相等即可得到D到AC的距离是5.
【答案】5
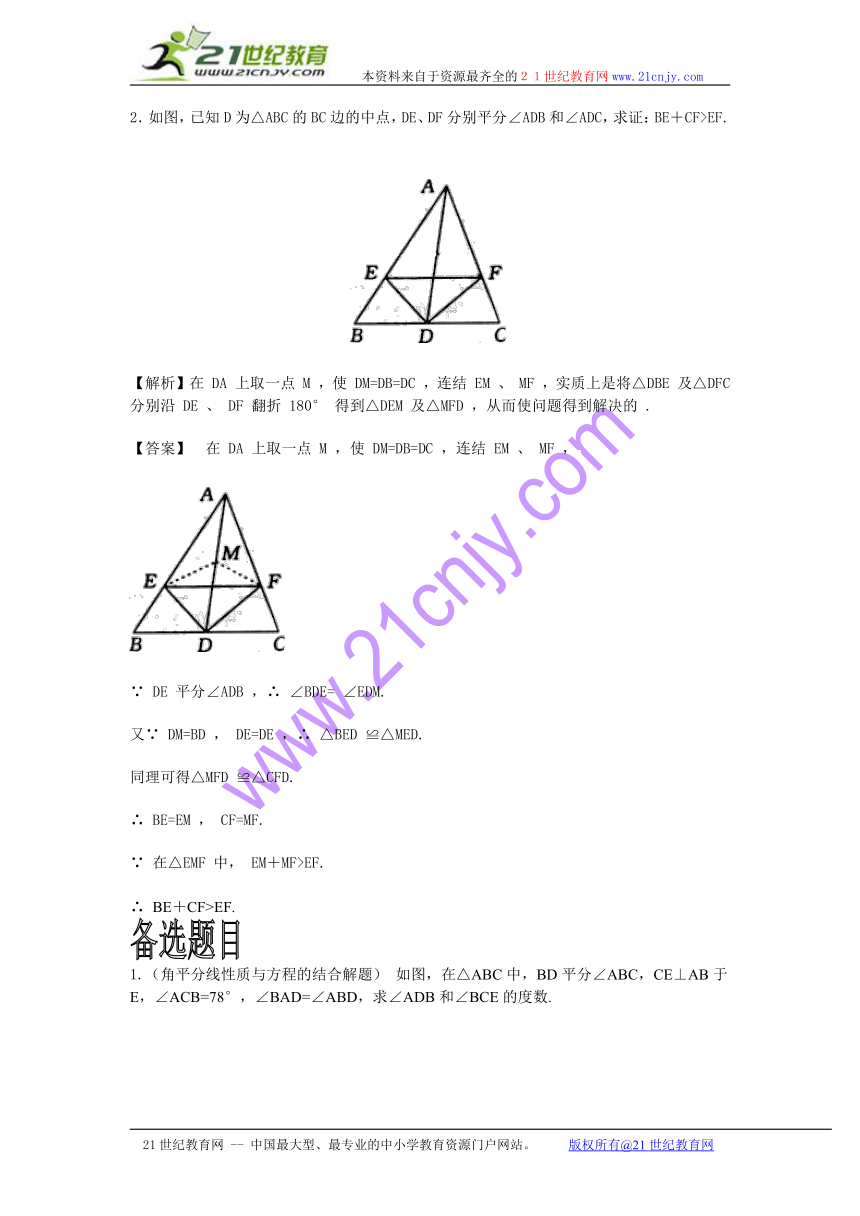
2.如图,已知D为△ABC的BC边的中点,DE、DF分别平分∠ADB和∠ADC,求证:BE+CF>EF.
【解析】在 DA 上取一点 M ,使 DM=DB=DC ,连结 EM 、 MF ,实质上是将△DBE 及△DFC 分别沿 DE 、 DF 翻折 180° 得到△DEM 及△MFD ,从而使问题得到解决的 .
【答案】?在 DA 上取一点 M ,使 DM=DB=DC ,连结 EM 、 MF ,
∵ DE 平分∠ADB ,∴ ∠BDE= ∠EDM.
又∵ DM=BD , DE=DE ,∴ △BED ≌△MED.
同理可得△MFD ≌△CFD.
∴ BE=EM , CF=MF.
∵ 在△EMF 中, EM+MF>EF.
∴ BE+CF>EF.
1.(角平分线性质与方程的结合解题) 如图,在△ABC中,BD平分∠ABC,CE⊥AB于E,∠ACB=78°,∠BAD=∠ABD,求∠ADB和∠BCE的度数.
【解析】要求∠ADB 及∠BCE 度数,依条件知∠DBC= ∠DBA= ∠DAB. 采用“间接设元”比“直接设元”更有利于沟通各已知量之间的关系, 所以设∠DBA 为 x. 设元后,再用三角形内角和定理作为等量关系列出方程 .
【答案】解:在△ABC 中,∵ BD 平分∠ABC ,
∴ ∠DBC= ∠DBA.
又∵∠DBA= ∠DAB ,设∠DBA=x ,那么∠DBC= ∠DAB=x.
又∠ACB=78°,∵ ∠DAB+∠ABC+∠ACB=180°,
∴ x+2x+78° =180°,解得 x=34°.
故在△ADB 中,∠ADB=180°-∠DAB-∠DBA=180°-2x=112° .
在△BCE 中,∵ CE⊥AB ,∴ ∠CEB=90° .
∴ ∠BCE=180°-∠CBE-∠CEB=180°-2x-90° =22° .
故∠ADB=112°,∠BCE=22° .
课时作业:
A等级
1.已知AD是△ABC的角平分线,DE⊥AB于E,且DE=3cm,则点D到AC的距离是( )
A.2cm B.3cm C.4cm D.6cm
2.如图,已知CE、CF分别是△ABC的内角和外角平分线,则图中与∠BCE互余的角有( )
A.4个 B.3个 C.2个 D.1个
3.如图,已知点P到AE、AD、BC的距离相等,则下列说法:①点P在∠BAC的平分线上;②点P在∠CBE的平分线上;③点P在∠BCD的平分线上;④点P是∠BAC、∠CBE、∠BCD的平分线的交点,其中正确的是( )
A.①②③④ B.①②③ C.④ D.②③
4.下列说法:①角的内部任意一点到角的两边的距离相等;②到角的两边距离相等的点在这个角的平分线上;③角的平分线上任意一点到角的两边的距离相等;④△ABC中∠BAC的平分线上任意一点到三角形的三边的距离相等,其中正确的( )
A.1个 B.2个 C.3个 D.4个
5.角的平分线上的点到_____________相等;到____________相等的点在这个角的平分线上.
6.如图,△ABC中,AC⊥CB,CD平分∠ACB,点E在AC上,且CE=CB,则下列结论:①CD平分∠BDE;②BD=DE;③∠B=∠CED;④∠A+∠CED=90°.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
7.∠AOB的平分线上一点M,M到OA的距离为1.5㎝,则M到OB的距离为 ㎝。
8.在△ABC中,∠C=90°,AD是∠BAC的角平分线,若BC=5㎝,BD=3㎝,则点D到AB的距离为 。
9.如图,∠A=90°,BD是△ABC的角平分线,AC=8㎝,DC=3DA,则点D到BC的距离为 。
10.如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是( )
A、PD=PE B、OD=OE C、∠DPO=∠EPO D、PD=OD
B等级
11.如图,AB=AD,∠ABC=∠ADC=90°,则下列结论:①∠3=∠4;②∠1=∠2;③∠5=∠6;④AC垂直且平分BD,其中正确的有( )
A.①②③④ B.①②③ C.①③ D.①③④
12.如图,三条公路两两交于点A、B、C,现要修一个货物中转站,要求到三条公路距离相等,则可供选择的地址有( )
A.一处 B.二处 C.三处 D.四处
13.△ABC中,∠C=90°,AD平分∠BAC交BC于D,且BD:CD=3:2,BC=15cm,则点D到AB的距离是__________.
14.如图,已知点D是△ABC中AC边一点,点E在AB延长线上,且△ABC≌△DBE,∠BDA=∠A.若∠A:∠C=5:3,则∠DBE的度数是( )
A.100° B.80° C.60° D.120°
15.如图,已知△ABC中,∠C=90°,E是AB的中点,D在∠B的平分线上,且DE⊥AB,则( )
A.BD<AE B.BC=AE C.BC<AE D.以上都不对
16.如图,AB=AD,∠ABC=∠ADC=90°,则下列结论:①∠3=∠4;②∠1=∠2;③∠5=∠6;④AC垂直且平分BD,其中正确的有( )
A.①②③④ B.①②③ C.①③ D.①③④
17.已知:如图⑷,P是∠AOB的平分线上的一点,PC⊥OA于C,PD⊥OB于D,写出图中一组相等的线段 (只需写出一组即可).
18.如图,AB∥CD,AP、CP分别平分∠BAC和∠ACD,PE⊥AC于E,且PE=2cm,则AB与CD之间的距离是___________.
19.用直尺和圆规平分已知角的依据是______________.
20.到三角形三边的距离相等的点是三角形( )
A.三条边上的高的交点 B.三个内角平分线的交点
C.三边上的中线的交点 D.以上结论都不对
C等级
21.如图△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=6㎝,则△DEB的周长为( )
A、4㎝ B、6㎝ C、10㎝ D、不能确定
22.如图,MP⊥NP,MQ为△MNP的角平分线,MT=MP,连接TQ,则下列结论中不正确的是( )
A、TQ=PQ B、∠MQT=∠MQP C、∠QTN=90° D、∠NQT=∠MQT
23.如图,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且DB=DC,
求证:BE=CF。
24.已知,如图BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于D,求证:PM=PN。
25.如图,B是∠CAF内一点,D在AC上,E在AF上,且DC=EF,△BCD与△BEF的面积相等。求证:AB平分∠CAF。
26.如图,已知CD⊥AB于D,BE⊥AC于E,CD交BE于点O.
⑴若OC=OB,求证:点O在∠BAC的平分线上.
⑵若点O在∠BAC的平分线上,求证:OC=OB.
27.如图,四边形ABCD中,AB=AD,AB⊥BC,AD⊥CD,P是对角线AC上一点,求证:PB=PC。
28.如图,某铁路MN与公路PQ相交于点O且交角为90°,某仓库G在A区,到公、铁路距离相等,且到公路与铁路的相交点O的距离为200m。在图上标出仓库G的位置。(比例尺:1:10000。用尺规作图,保留作图痕迹,不写作法)
29.如图,已知点P是△ABC中BC边的中点,PD⊥AB于D,PE⊥AC于E.
①当PD=PE时,求证:AB=AC; ②当AB=AC时,求证:PD=PE。
30.请你画一个角,并用直尺和圆规把这个角两等分.
A等级答案
1.B
2.C
3.A
4.B
5.角的两边的距离;角的两边的距离
6.D
7.1.5
8.2
9.2cm
10.D
B等级答案
11.D
12.A
13.6cm
14.A
15.B
16.D
17.答案不惟一
18.4cm
19.SSS
20.B
C等级答案
21.B
22.D
23.因为AD是∠BAC的平分线,DE⊥AB,DF⊥AC,所以DE=DF,∠E=∠DFC=90°,因为BD=CD,所以RT△BDE≌RT△CDF,所以BE=CF
24.因为AB=BC,∠ABD=∠CBD,BD=BD,所以△ABD≌△CBD,所以∠ADB=∠CDB,因为PM⊥AD,PN⊥CD,所以PM=PN。
25.因为DC=EF,△DCB和△EFB面积想等,所以B到AC,AF的距离相等,所以AB平分∠CAF。
26.①证明△COE≌△BOD得到OE=OD;②先由角平分线的性质证明OE=OD,再证明△COE≌△BOD.
27.先证Rt△ABC≌Rt△ADC,再证△APB≌△APD.
28.作∠NOQ的平分线OP在OP上截取OG=2cm。
29.①连接AP,证明AD=AE和BD=CE;②证明AP平分∠BAC。
30.略
A
B
C
D
P
A
C
P
B
D
O
1
2
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第11章 全等三角形
(第三课时) 角的平分线的性质
本节主要通过介绍画角的平分线,引导学生发现问题:角的平分线有什么性质?通过将一个角对折的方法学习对角线的性质:在角的平分线上的点到这个角的两边的距离相等.利用三角形全等来说明角平分线的判定定理:到一个角的两边的距离相等的点在这个角的平分线上.接着引导学生试做一个三角形内的三个内角的角平分线,看看有什么特点,特点是:三角形的三条角平分线交于三角形内一点,并且这个点到三角形三边的距离相等.角的平分线的性质一课占有很重要的地位,它是证明线段相等、角相等的有利工具。
一.角的平分线的性质
这是本节的重点知识,但在以后的习题中很少会单独的出现只考查角平分线的性质的题目,一般会综合的考查三角形全等、平行线等有关知识,故在【知识点击】、【典例引路】、【当堂检测】、【基础训练】中设置了相应的例题以提高解题能力。
二.性质运用
在【备选题目】中,设置了角平分线与方程解决问题的题目,以提高学生的综合解题能力。
三.易错点
本节知识的易错点是,把角平分线的性质及角平分线的判断混淆了,所以在【典例引路】例3题及【基础训练】第3题设置了相应的题目。
点击一: 角平分线性质定理:在角的平分线上的点到这个角的两边的距离相等.
如图:AB是∠CAD的平分线,则有:CB=BD。
点击二: 角平分线判定定理:到一个角的两边的距离相等的点在这个角的平分线上.
如图:如果有CB=BD ,则有AB是∠CAD的平分线。
点击三: 三角形的三条角平分线交于三角形内一点,并且这个点到三角形三边的距离相等.
如图:在三角形ABC中,AD是∠BAC,BE是∠ABC的角平分线,则有IH=IG=IF。
类型之一:求证角平分线的性质定理
例1:三角形的三条角平分线交于一点,你知道这是为什么吗?
【解析】我们知道两条直线是交于一点的,因此可以想办法证明第三条角平分线通过前两条角平分线的交点.
【答案】已知:如图,△ABC的角平分线AD与BE交于点I,求证:点I在∠ACB的平分线上.
证明:过点I作IH⊥AB、IG⊥AC、IF⊥BC,垂足分别是点H、G、F.
∵点I在∠BAC的角平分线AD上,且IH⊥AB、IG⊥AC
∴IH=IG(角平分线上的点到角的两边距离相等)
同理 IH=IF ∴IG=IF(等量代换)
又IG⊥AC、IF⊥BC
∴点I在∠ACB的平分线上(到一个角的两边的距离相等的点,在这个角的平分线上)
即:三角形的三条角平分线交于一点.
类型之二:利用角平分线的性质求线段之比
例2:如图,已知:∠BAC=30,G为∠BAC的平分线上的一点,若EG ∥AC交AB于E,GD ⊥AC 于D,GD:GE=( )
【解析】作GF⊥AB于F(目的是为了用定理)
∵AG平分∠BAC,GD ⊥AC
∴ GF=GD(角平分线的性质定理)
∵ EG ∥AC ,∠BAC=300
∴∠FEG=300
∴FG:EG=1:2
∴GD:GE=1:2
【答案】1:2
类型之三: 利用角平分线的性质求角的度数
例3:在△ABC中,∠ABC=100,∠ACB=20,CE 平分∠ACB交 AB于 E,D在 AC上,且∠CBD=20。求∠CED的度数。
【解析】此题是考查利用角平分线的性质求角的度数。
【答案】作EF⊥ AC,延长CB,作EG ⊥CB
EH⊥ BD
∵CE平分∠ACB,∠ACB=200,
∴∠BCE=∠DCE=100,
∵∠CBD=200
∴ ∠ BDA=40 0
∵∠ABC=1000, ∠CBD=200
∴ ∠ABG=800,∠ABD=800
∴ ∠ABG=∠ABD
∴EH=EG
可证△BEH≌△ BEG(AAS)
∵CE平分∠ACB,
∴EF=EG(角平分线性质定理)
∴EF=EH
∴DE平分 ∠BDA(角平分线的判定定理)
∴∠EDA=200
∵∠EDA=∠ECA+∠CED
∴∠CED=200 -100=100
1. 如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C.下列结论错误的是( ).
A.AD=CP B.△ABP≌△CBP
C.△ABD≌△CBD D.∠ADB=∠CDB.
【解析】通过角平分线上的性质的运用推得△ABP≌△CBP ,△ABD≌△CBD ,∠ADB=∠CDB三项成立,A项不成立,能推出AD=DC,也能推得AP=PC。
【答案】A
2. 如图所示,AD⊥OB,BC⊥OA,垂足分别为D、C,AD与BC相交于点P,若PA=PB,则∠1与∠2的大小是()
A.∠1=∠2 B.∠1>∠2
C.∠1<∠2 D.无法确定
【解析】∵AD⊥OB,BC⊥OA,PA=PB,由角平分线的判定可知∠1=∠2.
【答案】A
3.△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=12cm,则△DBE的周长为()
A、12cm B、10cm C、14cm D、11cm
【解析】∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,易得△ACD≌△AED,
∴CD=DE,AE=AC,∴△DBE的周长=DE+EB+DE=CD+DB+EB=BC+EB=AC+EB=AE+EB=AB=12cm.
【答案】A
1. 已知AD是△ABC的角平分线,DE⊥AB于E,且DE=5cm,则点D到AC的距离是_____.
【解析】角平分线上的一点到角的两边距离相等即可得到D到AC的距离是5.
【答案】5
2.如图,已知D为△ABC的BC边的中点,DE、DF分别平分∠ADB和∠ADC,求证:BE+CF>EF.
【解析】在 DA 上取一点 M ,使 DM=DB=DC ,连结 EM 、 MF ,实质上是将△DBE 及△DFC 分别沿 DE 、 DF 翻折 180° 得到△DEM 及△MFD ,从而使问题得到解决的 .
【答案】?在 DA 上取一点 M ,使 DM=DB=DC ,连结 EM 、 MF ,
∵ DE 平分∠ADB ,∴ ∠BDE= ∠EDM.
又∵ DM=BD , DE=DE ,∴ △BED ≌△MED.
同理可得△MFD ≌△CFD.
∴ BE=EM , CF=MF.
∵ 在△EMF 中, EM+MF>EF.
∴ BE+CF>EF.
1.(角平分线性质与方程的结合解题) 如图,在△ABC中,BD平分∠ABC,CE⊥AB于E,∠ACB=78°,∠BAD=∠ABD,求∠ADB和∠BCE的度数.
【解析】要求∠ADB 及∠BCE 度数,依条件知∠DBC= ∠DBA= ∠DAB. 采用“间接设元”比“直接设元”更有利于沟通各已知量之间的关系, 所以设∠DBA 为 x. 设元后,再用三角形内角和定理作为等量关系列出方程 .
【答案】解:在△ABC 中,∵ BD 平分∠ABC ,
∴ ∠DBC= ∠DBA.
又∵∠DBA= ∠DAB ,设∠DBA=x ,那么∠DBC= ∠DAB=x.
又∠ACB=78°,∵ ∠DAB+∠ABC+∠ACB=180°,
∴ x+2x+78° =180°,解得 x=34°.
故在△ADB 中,∠ADB=180°-∠DAB-∠DBA=180°-2x=112° .
在△BCE 中,∵ CE⊥AB ,∴ ∠CEB=90° .
∴ ∠BCE=180°-∠CBE-∠CEB=180°-2x-90° =22° .
故∠ADB=112°,∠BCE=22° .
课时作业:
A等级
1.已知AD是△ABC的角平分线,DE⊥AB于E,且DE=3cm,则点D到AC的距离是( )
A.2cm B.3cm C.4cm D.6cm
2.如图,已知CE、CF分别是△ABC的内角和外角平分线,则图中与∠BCE互余的角有( )
A.4个 B.3个 C.2个 D.1个
3.如图,已知点P到AE、AD、BC的距离相等,则下列说法:①点P在∠BAC的平分线上;②点P在∠CBE的平分线上;③点P在∠BCD的平分线上;④点P是∠BAC、∠CBE、∠BCD的平分线的交点,其中正确的是( )
A.①②③④ B.①②③ C.④ D.②③
4.下列说法:①角的内部任意一点到角的两边的距离相等;②到角的两边距离相等的点在这个角的平分线上;③角的平分线上任意一点到角的两边的距离相等;④△ABC中∠BAC的平分线上任意一点到三角形的三边的距离相等,其中正确的( )
A.1个 B.2个 C.3个 D.4个
5.角的平分线上的点到_____________相等;到____________相等的点在这个角的平分线上.
6.如图,△ABC中,AC⊥CB,CD平分∠ACB,点E在AC上,且CE=CB,则下列结论:①CD平分∠BDE;②BD=DE;③∠B=∠CED;④∠A+∠CED=90°.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
7.∠AOB的平分线上一点M,M到OA的距离为1.5㎝,则M到OB的距离为 ㎝。
8.在△ABC中,∠C=90°,AD是∠BAC的角平分线,若BC=5㎝,BD=3㎝,则点D到AB的距离为 。
9.如图,∠A=90°,BD是△ABC的角平分线,AC=8㎝,DC=3DA,则点D到BC的距离为 。
10.如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是( )
A、PD=PE B、OD=OE C、∠DPO=∠EPO D、PD=OD
B等级
11.如图,AB=AD,∠ABC=∠ADC=90°,则下列结论:①∠3=∠4;②∠1=∠2;③∠5=∠6;④AC垂直且平分BD,其中正确的有( )
A.①②③④ B.①②③ C.①③ D.①③④
12.如图,三条公路两两交于点A、B、C,现要修一个货物中转站,要求到三条公路距离相等,则可供选择的地址有( )
A.一处 B.二处 C.三处 D.四处
13.△ABC中,∠C=90°,AD平分∠BAC交BC于D,且BD:CD=3:2,BC=15cm,则点D到AB的距离是__________.
14.如图,已知点D是△ABC中AC边一点,点E在AB延长线上,且△ABC≌△DBE,∠BDA=∠A.若∠A:∠C=5:3,则∠DBE的度数是( )
A.100° B.80° C.60° D.120°
15.如图,已知△ABC中,∠C=90°,E是AB的中点,D在∠B的平分线上,且DE⊥AB,则( )
A.BD<AE B.BC=AE C.BC<AE D.以上都不对
16.如图,AB=AD,∠ABC=∠ADC=90°,则下列结论:①∠3=∠4;②∠1=∠2;③∠5=∠6;④AC垂直且平分BD,其中正确的有( )
A.①②③④ B.①②③ C.①③ D.①③④
17.已知:如图⑷,P是∠AOB的平分线上的一点,PC⊥OA于C,PD⊥OB于D,写出图中一组相等的线段 (只需写出一组即可).
18.如图,AB∥CD,AP、CP分别平分∠BAC和∠ACD,PE⊥AC于E,且PE=2cm,则AB与CD之间的距离是___________.
19.用直尺和圆规平分已知角的依据是______________.
20.到三角形三边的距离相等的点是三角形( )
A.三条边上的高的交点 B.三个内角平分线的交点
C.三边上的中线的交点 D.以上结论都不对
C等级
21.如图△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=6㎝,则△DEB的周长为( )
A、4㎝ B、6㎝ C、10㎝ D、不能确定
22.如图,MP⊥NP,MQ为△MNP的角平分线,MT=MP,连接TQ,则下列结论中不正确的是( )
A、TQ=PQ B、∠MQT=∠MQP C、∠QTN=90° D、∠NQT=∠MQT
23.如图,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且DB=DC,
求证:BE=CF。
24.已知,如图BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于D,求证:PM=PN。
25.如图,B是∠CAF内一点,D在AC上,E在AF上,且DC=EF,△BCD与△BEF的面积相等。求证:AB平分∠CAF。
26.如图,已知CD⊥AB于D,BE⊥AC于E,CD交BE于点O.
⑴若OC=OB,求证:点O在∠BAC的平分线上.
⑵若点O在∠BAC的平分线上,求证:OC=OB.
27.如图,四边形ABCD中,AB=AD,AB⊥BC,AD⊥CD,P是对角线AC上一点,求证:PB=PC。
28.如图,某铁路MN与公路PQ相交于点O且交角为90°,某仓库G在A区,到公、铁路距离相等,且到公路与铁路的相交点O的距离为200m。在图上标出仓库G的位置。(比例尺:1:10000。用尺规作图,保留作图痕迹,不写作法)
29.如图,已知点P是△ABC中BC边的中点,PD⊥AB于D,PE⊥AC于E.
①当PD=PE时,求证:AB=AC; ②当AB=AC时,求证:PD=PE。
30.请你画一个角,并用直尺和圆规把这个角两等分.
A等级答案
1.B
2.C
3.A
4.B
5.角的两边的距离;角的两边的距离
6.D
7.1.5
8.2
9.2cm
10.D
B等级答案
11.D
12.A
13.6cm
14.A
15.B
16.D
17.答案不惟一
18.4cm
19.SSS
20.B
C等级答案
21.B
22.D
23.因为AD是∠BAC的平分线,DE⊥AB,DF⊥AC,所以DE=DF,∠E=∠DFC=90°,因为BD=CD,所以RT△BDE≌RT△CDF,所以BE=CF
24.因为AB=BC,∠ABD=∠CBD,BD=BD,所以△ABD≌△CBD,所以∠ADB=∠CDB,因为PM⊥AD,PN⊥CD,所以PM=PN。
25.因为DC=EF,△DCB和△EFB面积想等,所以B到AC,AF的距离相等,所以AB平分∠CAF。
26.①证明△COE≌△BOD得到OE=OD;②先由角平分线的性质证明OE=OD,再证明△COE≌△BOD.
27.先证Rt△ABC≌Rt△ADC,再证△APB≌△APD.
28.作∠NOQ的平分线OP在OP上截取OG=2cm。
29.①连接AP,证明AD=AE和BD=CE;②证明AP平分∠BAC。
30.略
A
B
C
D
P
A
C
P
B
D
O
1
2
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
