国庆长假八年级数学辅导第12章 等腰三角形
文档属性
| 名称 | 国庆长假八年级数学辅导第12章 等腰三角形 |

|
|
| 格式 | rar | ||
| 文件大小 | 61.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-09-29 00:00:00 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第12章 轴对称
(第五课时)等腰三角形
等腰三角形是一种特殊的三角形,是我们重点研究的几种三角形之一.它具有一些特殊性质,利用这些性质,可以解决有关三角形的边、角的证明及计算问题,也可以利用性质来进行有关线段、角的证明及计算问题.
点击一: 等腰三角形性质
性质1 两个底角相等(简写为“等边对等角”)
性质2 底边的中线、高及顶角平分线三线合一.
性质3 等边三角形各内角都等于60°.
点击二: 等腰三角形判定定理
若一个三角形有两个角相等,那么两角所对边也相等.它与性质定理互为逆定理,判定也简写成“等角对等边”.
推论1 三个角相等的三角形是等边三角形.
推论2 有一个角是60°的等腰三角形是等边三角形.
推论3 直角三角形中,若有一个锐角为30°,则该角所对的直角边为斜边的一半.
点击三:辅助线
(一)为什么要添线
解证几何题,就是由已知出发,用形式逻辑的推理与量的计算,来探究新的、未知结果,一句话,就是要创造条件实现从已知向结论的转化,实现这一转化,要具体问题具体分析,而添设辅助线,正是创造转化条件的一部分,是为了联系几何元素之间的关系而架设的桥梁.
(二)添辅助线的目的
总目的在于沟通解题思路,创设由已知条件向所求结论过渡的条件,不可生硬 地机械照搬,而是随着解题思路而展开,某些条件不能直接与结论发生联系时,为发掘、创设这些条件联系的途径,来设想和决定在图中添什么线与怎样去添线,这正是理解添设辅助线方法的精髓.
(三)添线的原则、手段
(1)化分散为集中,就是通过添加辅助线将已知和未知的有关几何元素相对集中到同一个或几个相关基本几何图形中去,使之产生联系.
(2)化整体为部分,就是通过添线把复杂的几何图形分解为几个简单的几何图形,使问题化繁为简.
(3)化不规则为规则,即通过添线将不规则几何图形化为规则几何图形,使问题化难为易.
添线的常用手段是平移、旋转、对称、截取、延长等.
类型之一:证明型
例1. 求证:等腰三角形两腰的中线相等。
【解析】要证BD=CE,可考虑证△ABD≌△ACE,而∠A为公共角,AB=AC,所以只需证明AD=AE即能达到证明目的.
【解答】
已知:△ABC中AB=AC,BD、CE为中线,求证BD=CE.
证明:∵AB=AC, AE=EB, AD=DC
∴AE=AD.在△ABD和△ACE中,AB=AC,∠A=∠A AD=AE
∴△ABD≌△ACE
∴BD=CE.
类型之二:运用等腰三角形的性质与方程综合求角的度数
例2.等腰三角形一个外角为100°,求三内角度数.
【解析】本题利用三角形内角和及等腰三角形性质等边对等角,但要注意本题中外角是顶角的外角,还是底角的外角,在两种不同位置时,求得的结果不一样,本题有两解.
【解答】∵等腰三角形
∴两底角相等,设顶角为x,底角为y,则x+2y=180°
(1)当顶角的外角为100°时,顶角的外角等于两底角之和
∴2y=100°求得
(2)当底角的外角为100°时,底角y=180°-100°=80°求得
∴三内角为80°,50°,50°或20°,80°,80°
类型之三:比较角的大小
例3.△ABC中,AC>AB.求证:∠B>∠C.
【解析】本例是三角形中边角之间不等关系的一个重要结论:三角形中,若边不相等,则较大的边所对的角也较大,(简写为“大边对大角”)这一结论可帮助我们利用边的不等关系,证明角的不等关系.
【解答】
证明: ∵AC>AB ∴在AC上取AD=AB,连BD,∵∠ADB>∠C.
且∠ABD=∠ADB 又∵∠ABC>∠ABD ∴∠ABC>∠C.
1.等腰三角形的一个内角是80°,求它的另外两个角.
【解析】用分类讨论的思想方法来思考本题.若顶角是80°,则设底角为α,由三角形内角和得2α 80°=180°,∴α=50°.若底角是80°则设项角为β,由三角形内角和得2×80° β=180°,∴β=20°.
【答案】
①若顶角是80°,设底角为α,则有
2α80°=180°,
∴α=50°.
②若底角是80°,设顶角为β,则有
80°×2 β=180°,
∴β=20。
∴这个等腰三角形的另外两个角是50°,50°或80°,20°.
2. 等腰三角形的底角与顶角的度数之比为2∶1,则顶角为( )
A.72° B.36° C.36°或72° D.18°
【解析】设顶角为α,则底角为2α,由三角形的内角和可知,α 2×2α=180°,5α=180°,∴α=36°,这个三角形的顶角为36°,故正确答案为B项.
【答案】B
3.等腰三角形一边长为8,另一边长为4,则它的周长为 ______.
【解析】题中给出等腰三角形的两边长分别是8和4,但并没有给出哪一个是腰,哪一个是底,要分两种情况:①若腰是8,底是4,则另一腰是8,有4 8>8,满足三角形三边关系,∴8×2+4=20;
②若腰是4,底是8,则另一腰是4,有4+4=8,不满足三角形三边关系,∴这种情况不存在.∴这个三角形的周长为20.
【答案】20
4. △ABC中,AB=AC,D在AB上,E在AC延长线上,且BD=CE,DE交BC于P,求证:DP=EP.
【解析】构造等腰三角形及全等三角形,利用它们的性质及判定来证明线段相等.是本题的基本思路,设法构造一个与△PCE全等的三角形(或与△BDP全等的三角形),并使DP与PE成为对应边,是着手证本题的基本考虑.
【答案】
证明:过D作DF∥AC交BC于F,
∴∠FDP=∠E ∠DFB=∠ACB
∵AB=AC,∴∠B=∠ACB=∠DFB.
∴BD=DF又BD=CE,∴DF=CE
∴△DFP≌△ECP(AAS)
∴DP=PE
1.周长为21,边长都为整数的等腰三角形共有( )
A.4个 B.5个 C.8个 D.10个
【解析】设底边为x,腰长为y,∴x+2y=21.
∵2y为偶数,21为奇数 ∴x为奇数.
又三角形两边之和大于第三边 ∴x<2y.
x+2y>2x 2x<21 x<10.5.
x为奇数 ∴x=1,3,5,7,8 共5个
注x=7时,y=7为等边三角形,属特殊等腰三角形.
【答案】B
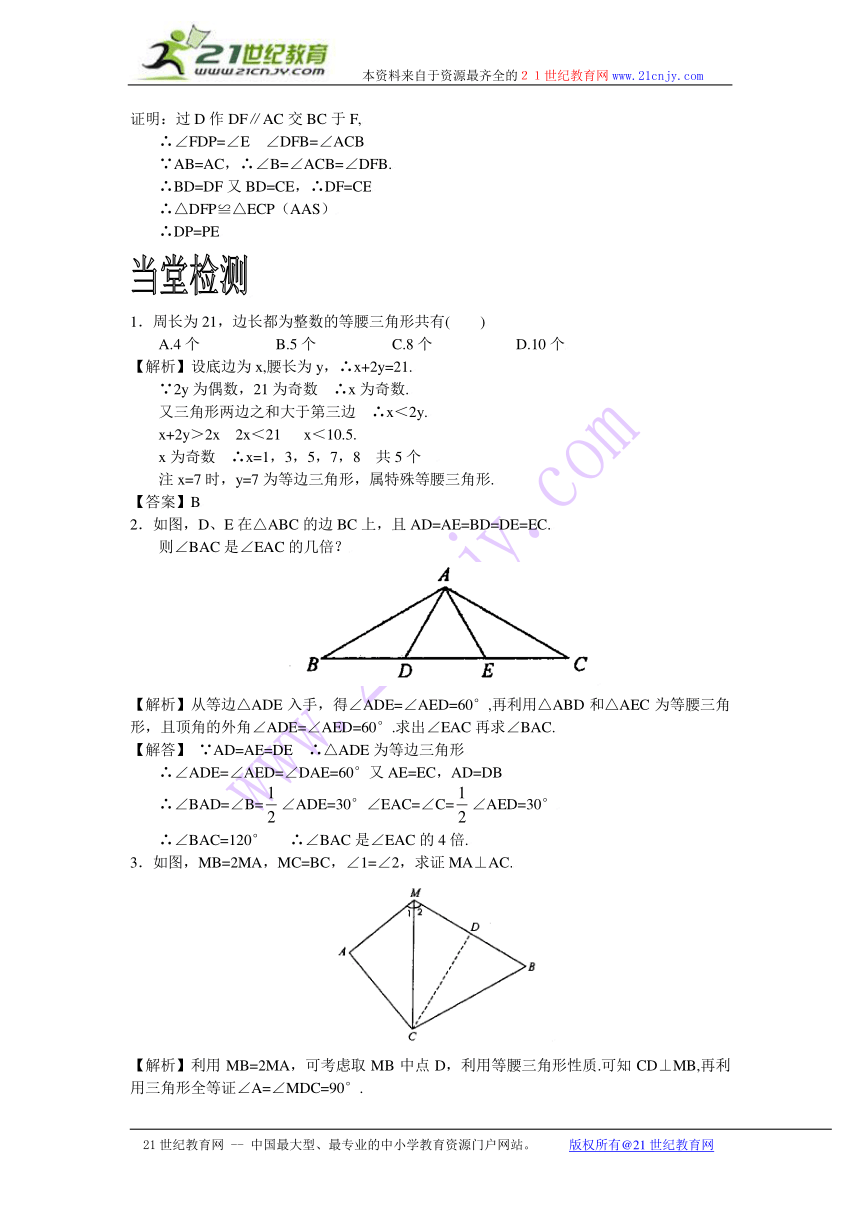
2.如图,D、E在△ABC的边BC上,且AD=AE=BD=DE=EC.
则∠BAC是∠EAC的几倍?
【解析】从等边△ADE入手,得∠ADE=∠AED=60°,再利用△ABD和△AEC为等腰三角形,且顶角的外角∠ADE=∠AED=60°.求出∠EAC再求∠BAC.
【解答】 ∵AD=AE=DE ∴△ADE为等边三角形
∴∠ADE=∠AED=∠DAE=60°又AE=EC,AD=DB
∴∠BAD=∠B=∠ADE=30°∠EAC=∠C=∠AED=30°
∴∠BAC=120° ∴∠BAC是∠EAC的4倍.
3.如图,MB=2MA,MC=BC,∠1=∠2,求证MA⊥AC.
【解析】利用MB=2MA,可考虑取MB中点D,利用等腰三角形性质.可知CD⊥MB,再利用三角形全等证∠A=∠MDC=90°.
【解答】
证明:作△MCB的中线CD.∵MB=2MA ∴MA=MD
又∠1=∠2 MC=MC ∴△MAC≌△MDC. ∠A=∠MDC
又MC=BC,CD为△MCB中线 ∴CD⊥MB ∠CDM=90°
∴∠A=90° ∴MA⊥AC.
1. 如图,D为等边三角形△ABC内一点,DA=DB,∠DBP=∠DBC.BP=BC,求∠P的度数.
【解析】正三角形内角为60°,可考虑将∠P与三角形内角进行联系,借用内角60°以达解题目的,连DC后易得△PBD≌△CBD,从而将求∠P转化为求∠DCB.
【解答】
连DC ∵BP=BC ∠PBD=∠CBD BD=BD
∴△PBD≌△CBD.
∴∠P=∠DCB. 又BD=AD CD=CD AC=BC
∴△BCD≌△ACD ∴∠BCD=∠ACD=∠ACB=×60°=30°
∴ ∠P=30°
2.△ABC中AB=AC,P为形内一点,且PB>PC.如图,求证∠APC>∠APB。
【解析】这一类在等腰三角形、等边三角形等图形中出现的与形内一点相关的问题.常利用适当的旋转.使等边重合.将该点与三顶点的连线段相对集中到一个三角形内,再设法利用已知来解决问题.
【解答】∵AB=AC ∴将△ABP绕A点逆时针旋转,使AB与AC重合得△AP′C,连PP′由作图△ABP≌△ACP′
∴AP=AP′,BP=CP′
∴∠1=∠2 ∠APB=∠AP′C. P′C=BP>PC.
在△PP′C中,P′C>PC ∴∠3>∠4 ∠1+∠3>∠4+∠2.
∴∠APC>∠AP′C ∴∠APC>∠APB.
课时作业:
A等级
1. 在等腰三角形中,顶角的平分线与底边的关系是_______________。
2. 等腰三角形的两底角的平分线________;等腰三角形底边的中点到两腰的距离之比为_________
3. 若等腰三角形的两边长分别为5和6,则其周长为________;若等腰三角形的两边长分别为m和n,且m>2n,则其周长为________
4. 等腰三角形有一底角的外角为105o,那么它的顶角的度数为( )
A.30o B.40o C.45o D.60o
5. 已知D是△ABC的边BC上一点,且AB=AC=BD,那么∠ADB和∠CAD的关系为( )
A.∠ADB=2∠CAD B.2∠ADB+∠CAD=180o
C.∠ADB+2∠CAD=180o D.3∠ADB-∠CAD=180o
6. 等腰三角形中的一腰上的高与底边所成的角等于( )
A.顶角的一半 B.底角的一半
C.90o减去顶角的一半 D.90o减去底角的一半
7. 在等腰三角形中,如果一腰上的高等于腰长的一半,那么其顶角的度数为__________
8. 在△ABC中,AB=AC,∠BAC=120o,AB的垂直平分线交BC于点D,且BD=5cm,则DC=_________.
9. 在△ABC中,∠A=80o,点D,E,F分别在边BC,AB,AC上, BD=BE,CD=CF,则∠EDF的度数为_________.
10. 如图,在△ABC中,AB=AC,∠A=30 o,BE=CD,BD=CF,则EDF的度数为( )
A.80 o B.75 o C.65 o D.60 o
B等级
11. 在△ABC中,∠ABC=2∠ACB,BD平分∠ABC,AD∥BC,如图,则图中等腰三角形的个数是( )
A.1个 B.2个 C.3个 D.4个
12. 如图,△ABC中,∠B与∠C的平分线相交于O点,过O点作MN∥BC交AB。AC分别于M、N,若AB=12,AC=18,BC=24,则△AMN的周长为( )
A.30 B.36 C.39 D.42
13.D为等边三角形ABC边AC上一点,∠ACE=∠ABD,CE=BD.则△ADE是( )
A.钝角三角形 B.直角三角形
C.任意等腰三角形 D.等边三角形
14.AD为△ABC的角平分线,AB+BD=AC,则∠B∶∠C值为( )
A.2∶1 B.3∶1 C.4∶1 D.5∶1
15.△ABC中,∠A=∠C=55°,形内一点P使∠PAC=∠PCA,则∠ABP为( )
A.30° B.35° C.40° D.45°
16.△ABC中,AB=AC,∠BAC=120°,D 为BC上一点,DA⊥AB,AD=24则BC=( )
A.24 B.36 C.72 D.96
17.等腰直角三角形斜边长为a,则面积为( )
A.a2 B.a2 C.a2 D.2a2
18.如果一个三角形一条边上的中点到其它两边距离相等,那么这个三角形一定是( )
A.等边三角形 B.等腰三角形
C.直角三角形 D.斜三角形
19.△ABC中∠C=2∠B,则( )
A.AB<2AC B.AB=2AC
C.AB>2AC D.AB与2AC关系不确定.
20.如图,△ABC中AB=AC,∠A=36°,BD、CE为角平分线,交于O,则图中等腰三角形共有( )
A.4个 B.6个 C.8个 D.10个
C等级
21.三角形一个外角平分线平行三角形一边,则这个三角形是 .
22.等腰三角形一个外角为130°,则顶角为 .
23.三内角都相等的三角形是 三角形,每个内角都等于 .
24.△ABC中,AB=5,AC=7,∠B,∠C的平分线交于O,直线MN过O点交AB于M,AC于N,若MN∥BC,则△AMN周长为 .
25.△ABC中,高AD、BE交于H,且BH=AC,则∠ABC= .
26.△ABC中,∠C=2∠B,AC=4,则AB的取值范围 <AB< .
27.1.△ABC中,AB=AC,∠A=20°,D为AB上一点,且AD=BC,求∠BDC.
28.△ABC中,AB=AC,BD、CE为角平分线,AH⊥CE于F交BC于H,AG⊥BD于G.求证(1)AC=CH (2)AF=AG.
29.AD为△ABC的角平分线,M为BC中点,ME∥AD交BA延长线于E,交AC于F.求证BE=CF=(AB+AC)
30.Rt△ABC中,AC=BC,D为形内一点,满足∠DCB=∠DBC=15°.求证AC=AD.
A等级答案
1.垂直且平分底边
2.相等,1:1
3.16或17 ,m+2n
4.A
5.D
6.A
7.1.30 o或150 o
8.10cm
9.50°
10.B
B等级答案
11.D
12.A
13.D
14.A
15.B
16.C
17.A
18.B
19.A
20.C
C等级答案
21.等腰三角形
22.50°或80°
23.等边,60°
24.12
25.38° 7.45°
26.4<AB<8
27.作正△ACE ∠A=20° 连DE ∴∠DAE=∠B=80° AD=BC AE=AB
∴△ABC≌△EAD ∴DE=AC=CE,∠AED=∠A=20° ∠DEC=40° ∠DCE=70°
∴∠DCA=10° ∠BDC=30°
28.AH⊥CF CF平分∠ACH ∴△ACH为等腰三角形 ∴AC=CH.
∵AB=AC ∴∠ABC=∠ACB ∵BD,CE为角平分线 ∴∠ABD=∠ACE=
∠ABC=∠ACB ∴Rt△AGB≌Rt△AFC ∴AG=AF
29.延长EM到G,使MG=MF,连BG,则△BMG≌△CMF ∴BG=FC,∠G=∠CFM
又AD平分∠BAC AD∥ME, ∴∠E=∠BAD=∠DAC=∠MFC=∠G.∴BE=BG=FC
∴2BG=AB+AE+CF=AB+AF+CF=AB+AC ∴BE=CF=(AB+AC)
30.在△ACD内作正△CDP.连AP,∠DCB=15° ∠PCD=60° ∴∠ACP=∠DCB=15°
PC=CD BC=AC ∴△ACP≌△BCD ∴∠CAP=∠DBC=15° ∠APC=150°
∠CPD=60° ∴∠APD=150° ∴∠APC=∠APD PA=PA PC=PD
∴△PAC≌△PAD ∴AC=AD
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第12章 轴对称
(第五课时)等腰三角形
等腰三角形是一种特殊的三角形,是我们重点研究的几种三角形之一.它具有一些特殊性质,利用这些性质,可以解决有关三角形的边、角的证明及计算问题,也可以利用性质来进行有关线段、角的证明及计算问题.
点击一: 等腰三角形性质
性质1 两个底角相等(简写为“等边对等角”)
性质2 底边的中线、高及顶角平分线三线合一.
性质3 等边三角形各内角都等于60°.
点击二: 等腰三角形判定定理
若一个三角形有两个角相等,那么两角所对边也相等.它与性质定理互为逆定理,判定也简写成“等角对等边”.
推论1 三个角相等的三角形是等边三角形.
推论2 有一个角是60°的等腰三角形是等边三角形.
推论3 直角三角形中,若有一个锐角为30°,则该角所对的直角边为斜边的一半.
点击三:辅助线
(一)为什么要添线
解证几何题,就是由已知出发,用形式逻辑的推理与量的计算,来探究新的、未知结果,一句话,就是要创造条件实现从已知向结论的转化,实现这一转化,要具体问题具体分析,而添设辅助线,正是创造转化条件的一部分,是为了联系几何元素之间的关系而架设的桥梁.
(二)添辅助线的目的
总目的在于沟通解题思路,创设由已知条件向所求结论过渡的条件,不可生硬 地机械照搬,而是随着解题思路而展开,某些条件不能直接与结论发生联系时,为发掘、创设这些条件联系的途径,来设想和决定在图中添什么线与怎样去添线,这正是理解添设辅助线方法的精髓.
(三)添线的原则、手段
(1)化分散为集中,就是通过添加辅助线将已知和未知的有关几何元素相对集中到同一个或几个相关基本几何图形中去,使之产生联系.
(2)化整体为部分,就是通过添线把复杂的几何图形分解为几个简单的几何图形,使问题化繁为简.
(3)化不规则为规则,即通过添线将不规则几何图形化为规则几何图形,使问题化难为易.
添线的常用手段是平移、旋转、对称、截取、延长等.
类型之一:证明型
例1. 求证:等腰三角形两腰的中线相等。
【解析】要证BD=CE,可考虑证△ABD≌△ACE,而∠A为公共角,AB=AC,所以只需证明AD=AE即能达到证明目的.
【解答】
已知:△ABC中AB=AC,BD、CE为中线,求证BD=CE.
证明:∵AB=AC, AE=EB, AD=DC
∴AE=AD.在△ABD和△ACE中,AB=AC,∠A=∠A AD=AE
∴△ABD≌△ACE
∴BD=CE.
类型之二:运用等腰三角形的性质与方程综合求角的度数
例2.等腰三角形一个外角为100°,求三内角度数.
【解析】本题利用三角形内角和及等腰三角形性质等边对等角,但要注意本题中外角是顶角的外角,还是底角的外角,在两种不同位置时,求得的结果不一样,本题有两解.
【解答】∵等腰三角形
∴两底角相等,设顶角为x,底角为y,则x+2y=180°
(1)当顶角的外角为100°时,顶角的外角等于两底角之和
∴2y=100°求得
(2)当底角的外角为100°时,底角y=180°-100°=80°求得
∴三内角为80°,50°,50°或20°,80°,80°
类型之三:比较角的大小
例3.△ABC中,AC>AB.求证:∠B>∠C.
【解析】本例是三角形中边角之间不等关系的一个重要结论:三角形中,若边不相等,则较大的边所对的角也较大,(简写为“大边对大角”)这一结论可帮助我们利用边的不等关系,证明角的不等关系.
【解答】
证明: ∵AC>AB ∴在AC上取AD=AB,连BD,∵∠ADB>∠C.
且∠ABD=∠ADB 又∵∠ABC>∠ABD ∴∠ABC>∠C.
1.等腰三角形的一个内角是80°,求它的另外两个角.
【解析】用分类讨论的思想方法来思考本题.若顶角是80°,则设底角为α,由三角形内角和得2α 80°=180°,∴α=50°.若底角是80°则设项角为β,由三角形内角和得2×80° β=180°,∴β=20°.
【答案】
①若顶角是80°,设底角为α,则有
2α80°=180°,
∴α=50°.
②若底角是80°,设顶角为β,则有
80°×2 β=180°,
∴β=20。
∴这个等腰三角形的另外两个角是50°,50°或80°,20°.
2. 等腰三角形的底角与顶角的度数之比为2∶1,则顶角为( )
A.72° B.36° C.36°或72° D.18°
【解析】设顶角为α,则底角为2α,由三角形的内角和可知,α 2×2α=180°,5α=180°,∴α=36°,这个三角形的顶角为36°,故正确答案为B项.
【答案】B
3.等腰三角形一边长为8,另一边长为4,则它的周长为 ______.
【解析】题中给出等腰三角形的两边长分别是8和4,但并没有给出哪一个是腰,哪一个是底,要分两种情况:①若腰是8,底是4,则另一腰是8,有4 8>8,满足三角形三边关系,∴8×2+4=20;
②若腰是4,底是8,则另一腰是4,有4+4=8,不满足三角形三边关系,∴这种情况不存在.∴这个三角形的周长为20.
【答案】20
4. △ABC中,AB=AC,D在AB上,E在AC延长线上,且BD=CE,DE交BC于P,求证:DP=EP.
【解析】构造等腰三角形及全等三角形,利用它们的性质及判定来证明线段相等.是本题的基本思路,设法构造一个与△PCE全等的三角形(或与△BDP全等的三角形),并使DP与PE成为对应边,是着手证本题的基本考虑.
【答案】
证明:过D作DF∥AC交BC于F,
∴∠FDP=∠E ∠DFB=∠ACB
∵AB=AC,∴∠B=∠ACB=∠DFB.
∴BD=DF又BD=CE,∴DF=CE
∴△DFP≌△ECP(AAS)
∴DP=PE
1.周长为21,边长都为整数的等腰三角形共有( )
A.4个 B.5个 C.8个 D.10个
【解析】设底边为x,腰长为y,∴x+2y=21.
∵2y为偶数,21为奇数 ∴x为奇数.
又三角形两边之和大于第三边 ∴x<2y.
x+2y>2x 2x<21 x<10.5.
x为奇数 ∴x=1,3,5,7,8 共5个
注x=7时,y=7为等边三角形,属特殊等腰三角形.
【答案】B
2.如图,D、E在△ABC的边BC上,且AD=AE=BD=DE=EC.
则∠BAC是∠EAC的几倍?
【解析】从等边△ADE入手,得∠ADE=∠AED=60°,再利用△ABD和△AEC为等腰三角形,且顶角的外角∠ADE=∠AED=60°.求出∠EAC再求∠BAC.
【解答】 ∵AD=AE=DE ∴△ADE为等边三角形
∴∠ADE=∠AED=∠DAE=60°又AE=EC,AD=DB
∴∠BAD=∠B=∠ADE=30°∠EAC=∠C=∠AED=30°
∴∠BAC=120° ∴∠BAC是∠EAC的4倍.
3.如图,MB=2MA,MC=BC,∠1=∠2,求证MA⊥AC.
【解析】利用MB=2MA,可考虑取MB中点D,利用等腰三角形性质.可知CD⊥MB,再利用三角形全等证∠A=∠MDC=90°.
【解答】
证明:作△MCB的中线CD.∵MB=2MA ∴MA=MD
又∠1=∠2 MC=MC ∴△MAC≌△MDC. ∠A=∠MDC
又MC=BC,CD为△MCB中线 ∴CD⊥MB ∠CDM=90°
∴∠A=90° ∴MA⊥AC.
1. 如图,D为等边三角形△ABC内一点,DA=DB,∠DBP=∠DBC.BP=BC,求∠P的度数.
【解析】正三角形内角为60°,可考虑将∠P与三角形内角进行联系,借用内角60°以达解题目的,连DC后易得△PBD≌△CBD,从而将求∠P转化为求∠DCB.
【解答】
连DC ∵BP=BC ∠PBD=∠CBD BD=BD
∴△PBD≌△CBD.
∴∠P=∠DCB. 又BD=AD CD=CD AC=BC
∴△BCD≌△ACD ∴∠BCD=∠ACD=∠ACB=×60°=30°
∴ ∠P=30°
2.△ABC中AB=AC,P为形内一点,且PB>PC.如图,求证∠APC>∠APB。
【解析】这一类在等腰三角形、等边三角形等图形中出现的与形内一点相关的问题.常利用适当的旋转.使等边重合.将该点与三顶点的连线段相对集中到一个三角形内,再设法利用已知来解决问题.
【解答】∵AB=AC ∴将△ABP绕A点逆时针旋转,使AB与AC重合得△AP′C,连PP′由作图△ABP≌△ACP′
∴AP=AP′,BP=CP′
∴∠1=∠2 ∠APB=∠AP′C. P′C=BP>PC.
在△PP′C中,P′C>PC ∴∠3>∠4 ∠1+∠3>∠4+∠2.
∴∠APC>∠AP′C ∴∠APC>∠APB.
课时作业:
A等级
1. 在等腰三角形中,顶角的平分线与底边的关系是_______________。
2. 等腰三角形的两底角的平分线________;等腰三角形底边的中点到两腰的距离之比为_________
3. 若等腰三角形的两边长分别为5和6,则其周长为________;若等腰三角形的两边长分别为m和n,且m>2n,则其周长为________
4. 等腰三角形有一底角的外角为105o,那么它的顶角的度数为( )
A.30o B.40o C.45o D.60o
5. 已知D是△ABC的边BC上一点,且AB=AC=BD,那么∠ADB和∠CAD的关系为( )
A.∠ADB=2∠CAD B.2∠ADB+∠CAD=180o
C.∠ADB+2∠CAD=180o D.3∠ADB-∠CAD=180o
6. 等腰三角形中的一腰上的高与底边所成的角等于( )
A.顶角的一半 B.底角的一半
C.90o减去顶角的一半 D.90o减去底角的一半
7. 在等腰三角形中,如果一腰上的高等于腰长的一半,那么其顶角的度数为__________
8. 在△ABC中,AB=AC,∠BAC=120o,AB的垂直平分线交BC于点D,且BD=5cm,则DC=_________.
9. 在△ABC中,∠A=80o,点D,E,F分别在边BC,AB,AC上, BD=BE,CD=CF,则∠EDF的度数为_________.
10. 如图,在△ABC中,AB=AC,∠A=30 o,BE=CD,BD=CF,则EDF的度数为( )
A.80 o B.75 o C.65 o D.60 o
B等级
11. 在△ABC中,∠ABC=2∠ACB,BD平分∠ABC,AD∥BC,如图,则图中等腰三角形的个数是( )
A.1个 B.2个 C.3个 D.4个
12. 如图,△ABC中,∠B与∠C的平分线相交于O点,过O点作MN∥BC交AB。AC分别于M、N,若AB=12,AC=18,BC=24,则△AMN的周长为( )
A.30 B.36 C.39 D.42
13.D为等边三角形ABC边AC上一点,∠ACE=∠ABD,CE=BD.则△ADE是( )
A.钝角三角形 B.直角三角形
C.任意等腰三角形 D.等边三角形
14.AD为△ABC的角平分线,AB+BD=AC,则∠B∶∠C值为( )
A.2∶1 B.3∶1 C.4∶1 D.5∶1
15.△ABC中,∠A=∠C=55°,形内一点P使∠PAC=∠PCA,则∠ABP为( )
A.30° B.35° C.40° D.45°
16.△ABC中,AB=AC,∠BAC=120°,D 为BC上一点,DA⊥AB,AD=24则BC=( )
A.24 B.36 C.72 D.96
17.等腰直角三角形斜边长为a,则面积为( )
A.a2 B.a2 C.a2 D.2a2
18.如果一个三角形一条边上的中点到其它两边距离相等,那么这个三角形一定是( )
A.等边三角形 B.等腰三角形
C.直角三角形 D.斜三角形
19.△ABC中∠C=2∠B,则( )
A.AB<2AC B.AB=2AC
C.AB>2AC D.AB与2AC关系不确定.
20.如图,△ABC中AB=AC,∠A=36°,BD、CE为角平分线,交于O,则图中等腰三角形共有( )
A.4个 B.6个 C.8个 D.10个
C等级
21.三角形一个外角平分线平行三角形一边,则这个三角形是 .
22.等腰三角形一个外角为130°,则顶角为 .
23.三内角都相等的三角形是 三角形,每个内角都等于 .
24.△ABC中,AB=5,AC=7,∠B,∠C的平分线交于O,直线MN过O点交AB于M,AC于N,若MN∥BC,则△AMN周长为 .
25.△ABC中,高AD、BE交于H,且BH=AC,则∠ABC= .
26.△ABC中,∠C=2∠B,AC=4,则AB的取值范围 <AB< .
27.1.△ABC中,AB=AC,∠A=20°,D为AB上一点,且AD=BC,求∠BDC.
28.△ABC中,AB=AC,BD、CE为角平分线,AH⊥CE于F交BC于H,AG⊥BD于G.求证(1)AC=CH (2)AF=AG.
29.AD为△ABC的角平分线,M为BC中点,ME∥AD交BA延长线于E,交AC于F.求证BE=CF=(AB+AC)
30.Rt△ABC中,AC=BC,D为形内一点,满足∠DCB=∠DBC=15°.求证AC=AD.
A等级答案
1.垂直且平分底边
2.相等,1:1
3.16或17 ,m+2n
4.A
5.D
6.A
7.1.30 o或150 o
8.10cm
9.50°
10.B
B等级答案
11.D
12.A
13.D
14.A
15.B
16.C
17.A
18.B
19.A
20.C
C等级答案
21.等腰三角形
22.50°或80°
23.等边,60°
24.12
25.38° 7.45°
26.4<AB<8
27.作正△ACE ∠A=20° 连DE ∴∠DAE=∠B=80° AD=BC AE=AB
∴△ABC≌△EAD ∴DE=AC=CE,∠AED=∠A=20° ∠DEC=40° ∠DCE=70°
∴∠DCA=10° ∠BDC=30°
28.AH⊥CF CF平分∠ACH ∴△ACH为等腰三角形 ∴AC=CH.
∵AB=AC ∴∠ABC=∠ACB ∵BD,CE为角平分线 ∴∠ABD=∠ACE=
∠ABC=∠ACB ∴Rt△AGB≌Rt△AFC ∴AG=AF
29.延长EM到G,使MG=MF,连BG,则△BMG≌△CMF ∴BG=FC,∠G=∠CFM
又AD平分∠BAC AD∥ME, ∴∠E=∠BAD=∠DAC=∠MFC=∠G.∴BE=BG=FC
∴2BG=AB+AE+CF=AB+AF+CF=AB+AC ∴BE=CF=(AB+AC)
30.在△ACD内作正△CDP.连AP,∠DCB=15° ∠PCD=60° ∴∠ACP=∠DCB=15°
PC=CD BC=AC ∴△ACP≌△BCD ∴∠CAP=∠DBC=15° ∠APC=150°
∠CPD=60° ∴∠APD=150° ∴∠APC=∠APD PA=PA PC=PD
∴△PAC≌△PAD ∴AC=AD
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
