重庆市渝西中学2023-2024学年高二下学期6月月考数学试卷(含解析)
文档属性
| 名称 | 重庆市渝西中学2023-2024学年高二下学期6月月考数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-02 07:52:33 | ||
图片预览




文档简介
重庆市渝西中学2023-2024学年高二下学期6月月考数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.命题,的否定为( )
A., B.,
C., D.,
2.集合,,若,则实数( )
A.-1 B.0 C. D.1
3.已知,,则的取值范围是( )
A. B. C. D.
4.已知变量x,y呈线性相关关系,回归方程为,且变量x,y的样本数据如下表所示
x -2 -1 0 1 2
y 5 4 m 2 1
据此计算出在时,预测值为-0.2,则m的值为( )
A.3 B.2.8 C.2 D.1
5.已知实数,则下列不等式中一定正确的有( )
A. B. C. D.
6.已知偶函数在上单调递减,则,,的大小关系为( )
A. B. C. D.
7.把二项式的所有展开项重新排列,记有理项都相邻的概率为p,有理项两两不相邻的概率为q,则( )
A.5 B. C.4 D.
8.对于正数a,b,有,则的取值范围是( )
A. B. C. D.
二、多项选择题
9.随机变量X,Y分别服从正态分布和二项分布,即,,则( )
A. B. C. D.
10.已知函数的定义域为R,则p的必要条件可以是( )
A.或 B. C. D.
11.已知,,若对,使成立,则下列说法正确的是( )
A.函数的最小值为0 B.当时,的解集为
C.实数a的取值范围是 D.实数a的取值范围是
三、填空题
12.函数的定义域是____________.
13.2024年伊始,随着“广西沙糖桔”“马铃薯公主”等热梗的不断爆出,哈尔滨火爆出圈,成为旅游城市中的“顶流”.某班级五位同学也准备共赴一场冰雪之约,制定了“南方小土豆,勇闯哈尔滨”的出游计划,这五位同学准备在行程第一天在圣索菲亚教堂,冰雪大世界,中央大街三个景点中选择一个去游玩,已知每个景点至少有一位同学会选,五位同学都会进行选择并且只能选择其中一个景点,若学生甲和学生乙准备选同一个景点,则不同的选法种数是________.
14.设是定义在R上的单调增函数,且满足,若对于任意非零实数x都有,则_____________.
四、解答题
15.已知等差数列的前n项和为,且满足,.
(1)求数列的通项公式;
(2)若数列满足 求数列的前n项和.
16.新能源渗透率是指在一定时期内,新能源汽车销量占汽车总销量的比重.在2022年,新能源汽车的渗透率达到了,提前三年超过了“十四五”预定的的目标.2023年,随着技术进步,新能源车的渗透率还在继续扩大.将2023年1月视为第一个月,得到2023年1-10月,我国新能源汽车渗透率如下表:
月份代码x 1 2 3 4 5 6 7 8 9 10
渗透率 29 32 34 32 33 34 36 36 36 38
(1)假设自2023年1月起的第x个月的新能源渗透率为,试求y关于x的回归直线方程,并由此预测2024年1月的新能源渗透率;
(2)为了鼓励大家购买新能源汽车,国家在2024年继续执行新能源车购置税优惠政策:在2024年6月1日前购买的新能源车无需支付购置税,而燃油车需按照车价支付购置税.2024年1月小张为自己的客户代付购置税,当月他的客户购买了3辆车价格均为20万元,假设以(1)中预测的新能源渗透率作为当月客户购买新能源车的概率,设小张总共需要代付的购置税为X万元,求X的分布列和期望.
附:一组数据,,的线性回归直线方程的系数公式为:,
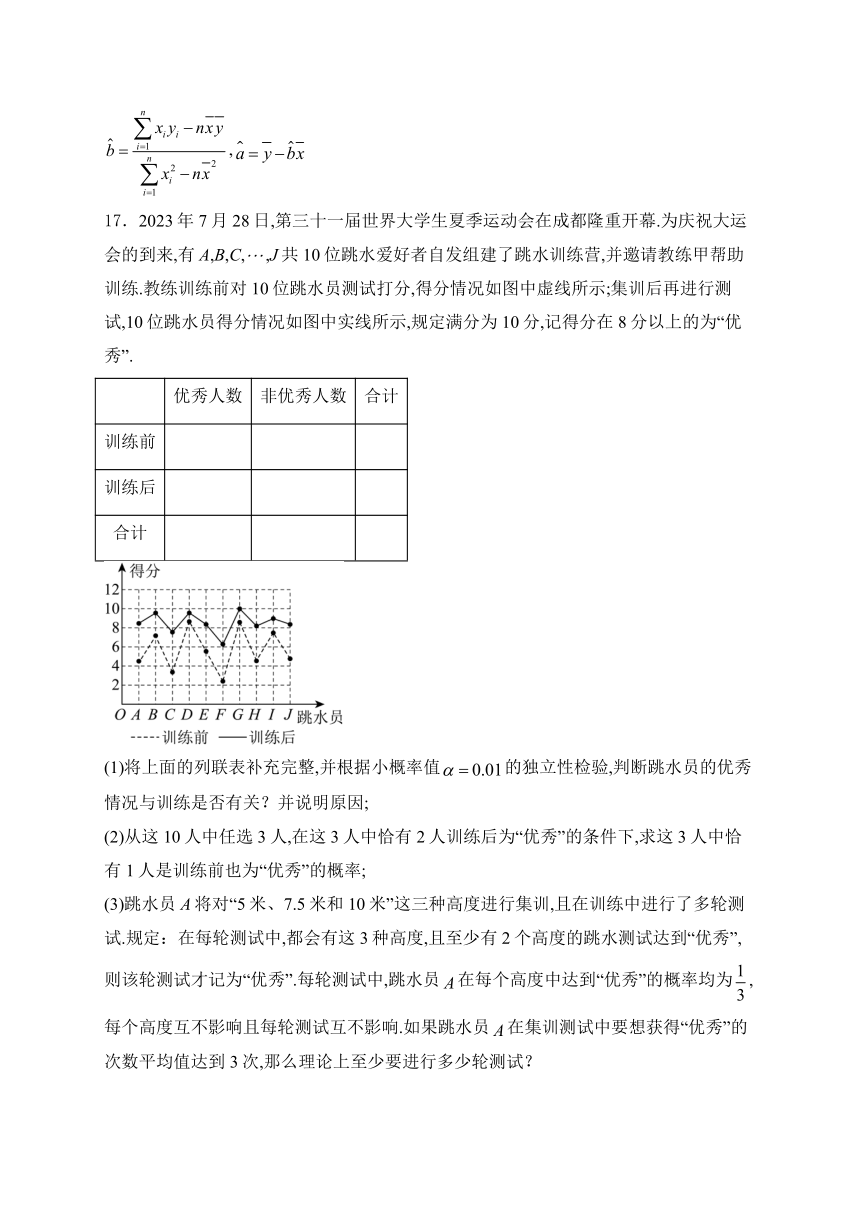
17.2023年7月28日,第三十一届世界大学生夏季运动会在成都隆重开幕.为庆祝大运会的到来,有A,B,C,,J共10位跳水爱好者自发组建了跳水训练营,并邀请教练甲帮助训练.教练训练前对10位跳水员测试打分,得分情况如图中虚线所示;集训后再进行测试,10位跳水员得分情况如图中实线所示,规定满分为10分,记得分在8分以上的为“优秀”.
优秀人数 非优秀人数 合计
训练前
训练后
合计
(1)将上面的列联表补充完整,并根据小概率值的独立性检验,判断跳水员的优秀情况与训练是否有关?并说明原因;
(2)从这10人中任选3人,在这3人中恰有2人训练后为“优秀”的条件下,求这3人中恰有1人是训练前也为“优秀”的概率;
(3)跳水员A将对“5米、7.5米和10米”这三种高度进行集训,且在训练中进行了多轮测试.规定:在每轮测试中,都会有这3种高度,且至少有2个高度的跳水测试达到“优秀”,则该轮测试才记为“优秀”.每轮测试中,跳水员在每个高度中达到“优秀”的概率均为,每个高度互不影响且每轮测试互不影响.如果跳水员在集训测试中要想获得“优秀”的次数平均值达到3次,那么理论上至少要进行多少轮测试?
附:,其中.
0.05 0.01 0.005 0.001
3.841 6.635 7.879 10.828
18.已知函数,,.
(1)当时,讨论的单调性;
(2)若曲线在点处的切线与曲线也相切,求实数a的值;
(3)若不等式对任意的恒成立,求a的取值范围.为自然对数的底数)
19.椭圆的左右焦点为和,O为椭圆的中心,过作直线、,分别交椭圆C于A、B和C、D,且的最大值为,的最小值为.
(1)求椭圆C的方程;
(2)设线段、的中点分别为M、N,记的面积为,的面积为,若直线、的斜率为、且,求证:为定值,并求出这个定值.
参考答案
1.答案:A
解析:命题,的否定为:,.
故选:A.
2.答案:C
解析:因为,故.
①当时,,则,与元素的互异性矛盾,故不成立;
②当时,解得,与元素的互异性矛盾,故不成立;
③当时,即,则,,故成立,故.
故选:C.
3.答案:D
解析:设,
所以,解得,所以;
又,,所以,
故选:D.
4.答案:C
解析:由题意知回归方程为过点,则,
即;
又,,
由于回归方程为必过样本中心点,
故,
故选:C.
5.答案:D
解析:对于A,当,时,,故A错误;
对于B,因为,,所以,又,,故,
从而,故B错误;
对于C,,
因为,所以,故,
故,故C错误;
对于D,
,
因为,故,
所以,即,故D正确.
故选:D.
6.答案:C
解析:因为为偶函数,故,
又因为,且,故,则.
故,又在上单调递减,
则,即.
故.
故选:C.
7.答案:A
解析:,其中,,
当时为有理项,故有5项有理项,4项无理项,
故,,故.
故选:A.
8.答案:C
解析:由题可知:(当且仅当时取等),
化简可得,解得.
9.答案:ABC
解析:A选项,根据正态分布的定义得,故A正确;
B选项,,,故,故B正确;
C选项,,,故,故C正确;
D选项,,故D错误.
故选:ABC.
10.答案:AB
解析:由题,恒成立,易知时不满足,
时,有.
故选:AB.
11.答案:AD
解析:对于A,令,则,(其中),
故,解得,
即,所以函数的最小值为0,所以A正确,
对于B,当时,由,得,解得,所以B错误,
对于CD,由题可知,,,即对,,
令,当时,取得最小值,
即,所以,所以C错误,D正确,
故选:AD
12.答案:
解析:由题意得,解得,
所以函数的定义域为,
故答案为:.
13.答案:36
解析:若甲乙选的景点没有其他人选,则分组方式为:1,2,2的选法总数为:,
若甲乙选的景点还有其他人选择,则分组方式为:1,1,3的选法总数为:,
所以不同的选法总数为:.
故答案为:36.
14.答案:2021
解析:令,则,令,
则,解得或.
而,故.因此.则,
即.
因此或,当时,,
在上单调递减,不满足题意,舍去;当时,满足题意.则.
15.答案:(1)
(2)
解析:(1)设等差数列的公差为d,则,
解得,故;
(2)由(1)可得,
故
.
16.答案:(1),
(2)分布列见解析,万元
解析:(1)计算得,,
所以,
,
则回归直线方程为,代入得,
所以预测2024年1月新能源渗透率为;
(2)由题意,每个客户购买新能源车的概率为,燃油车概率为,
X所有可能取值为0,2,4,6,
则,
,
,
,
所以X的分布列为
X 0 2 4 6
P
所以(万元).
17.答案:(1)列联表见解析,有关,原因见解析
(2)
(3)12轮
解析:(1)零假设:假设跳水员的优秀情况与训练无关.
列联表为:
优秀人数 非优秀人数 合计
训练前 2 8 10
训练后 8 2 10
合计 10 10 20
,
故根据小概率值的独立性检验,零假设不成立,即跳水员的优秀情况与训练有关,此推断犯错误的概率不超过0.01.
(2)由图可知:训练前后均不优秀的有C,F共2人,训练前后均优秀的有D,G共2人,训练前不优秀而训练后优秀的有6人,
设“所选3人中恰有2人训练后为优秀”,“所选3人中恰有1人训练前为优秀”,
则,,
(3)设跳水员A每轮测试为优秀的概率为P,则.
设A测试次数为n,则优秀的次数,
故,
故至少需进行12轮测试.
18.答案:(1)答案见解析
(2)
(3)
解析:(1)因为,,
所以,
当时,,在上单调递增;
当时,在上单调递减;
当时,令,则,
当时,,单调递减;
当时,,单调递增;
综上:当时,在上单调递增;
当时,在单调递减,在单调递增;
当时,在上单调递减;
(2)函数,,
所以,,,
故曲线在点处的切线方程为,
即.
设切线与曲线切于点,
则,
解得.
(3)法一:函数,定义域为,
故,
等价于,
记,,
令,,
解得,,解得,
故在上单调递减,在上单调递增,
所以当时,.
所以解得,,解得,
故在单调递减,在单调递增,
有,
所以a的取值范围为.
法二:取,由,得.
下证:当时,恒成立.
记,
因,函数在单调递减,
所以,
记,,
,,
记,,
,解得,,解得,
故在单调递减,在单调递增,
故,
故,在上单调递增,即在上单调递增,
又,
在上恒成立,在恒成立,
所以在单调递减,在单调递增,
所以,得证.
综上知,a的取值范围为.
19.答案:(1)
(2)证明见解析,
解析:(1)由已知得当在x轴上时,,
当在x轴上时,最小,此时直线方程为:,
联立,解得,所以,所以,,
故椭圆方程为.
(2)由(1)得,,设直线,,
其中,,则.
由消去x得:,,
设,,,则,,
,,
即,用代换同理可得,
解法一:设直线的斜率为k,
则.
故直线的方程为,
即,
将代入得,故直线恒过定点,
于是点O与点到直线的距离之比等于,从而.
解法二:对于一个,若,,则,
证明如下:
因为,
所以,
所以,
所以;
故对于,,
所以,
又,,
则,
所以.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.命题,的否定为( )
A., B.,
C., D.,
2.集合,,若,则实数( )
A.-1 B.0 C. D.1
3.已知,,则的取值范围是( )
A. B. C. D.
4.已知变量x,y呈线性相关关系,回归方程为,且变量x,y的样本数据如下表所示
x -2 -1 0 1 2
y 5 4 m 2 1
据此计算出在时,预测值为-0.2,则m的值为( )
A.3 B.2.8 C.2 D.1
5.已知实数,则下列不等式中一定正确的有( )
A. B. C. D.
6.已知偶函数在上单调递减,则,,的大小关系为( )
A. B. C. D.
7.把二项式的所有展开项重新排列,记有理项都相邻的概率为p,有理项两两不相邻的概率为q,则( )
A.5 B. C.4 D.
8.对于正数a,b,有,则的取值范围是( )
A. B. C. D.
二、多项选择题
9.随机变量X,Y分别服从正态分布和二项分布,即,,则( )
A. B. C. D.
10.已知函数的定义域为R,则p的必要条件可以是( )
A.或 B. C. D.
11.已知,,若对,使成立,则下列说法正确的是( )
A.函数的最小值为0 B.当时,的解集为
C.实数a的取值范围是 D.实数a的取值范围是
三、填空题
12.函数的定义域是____________.
13.2024年伊始,随着“广西沙糖桔”“马铃薯公主”等热梗的不断爆出,哈尔滨火爆出圈,成为旅游城市中的“顶流”.某班级五位同学也准备共赴一场冰雪之约,制定了“南方小土豆,勇闯哈尔滨”的出游计划,这五位同学准备在行程第一天在圣索菲亚教堂,冰雪大世界,中央大街三个景点中选择一个去游玩,已知每个景点至少有一位同学会选,五位同学都会进行选择并且只能选择其中一个景点,若学生甲和学生乙准备选同一个景点,则不同的选法种数是________.
14.设是定义在R上的单调增函数,且满足,若对于任意非零实数x都有,则_____________.
四、解答题
15.已知等差数列的前n项和为,且满足,.
(1)求数列的通项公式;
(2)若数列满足 求数列的前n项和.
16.新能源渗透率是指在一定时期内,新能源汽车销量占汽车总销量的比重.在2022年,新能源汽车的渗透率达到了,提前三年超过了“十四五”预定的的目标.2023年,随着技术进步,新能源车的渗透率还在继续扩大.将2023年1月视为第一个月,得到2023年1-10月,我国新能源汽车渗透率如下表:
月份代码x 1 2 3 4 5 6 7 8 9 10
渗透率 29 32 34 32 33 34 36 36 36 38
(1)假设自2023年1月起的第x个月的新能源渗透率为,试求y关于x的回归直线方程,并由此预测2024年1月的新能源渗透率;
(2)为了鼓励大家购买新能源汽车,国家在2024年继续执行新能源车购置税优惠政策:在2024年6月1日前购买的新能源车无需支付购置税,而燃油车需按照车价支付购置税.2024年1月小张为自己的客户代付购置税,当月他的客户购买了3辆车价格均为20万元,假设以(1)中预测的新能源渗透率作为当月客户购买新能源车的概率,设小张总共需要代付的购置税为X万元,求X的分布列和期望.
附:一组数据,,的线性回归直线方程的系数公式为:,
17.2023年7月28日,第三十一届世界大学生夏季运动会在成都隆重开幕.为庆祝大运会的到来,有A,B,C,,J共10位跳水爱好者自发组建了跳水训练营,并邀请教练甲帮助训练.教练训练前对10位跳水员测试打分,得分情况如图中虚线所示;集训后再进行测试,10位跳水员得分情况如图中实线所示,规定满分为10分,记得分在8分以上的为“优秀”.
优秀人数 非优秀人数 合计
训练前
训练后
合计
(1)将上面的列联表补充完整,并根据小概率值的独立性检验,判断跳水员的优秀情况与训练是否有关?并说明原因;
(2)从这10人中任选3人,在这3人中恰有2人训练后为“优秀”的条件下,求这3人中恰有1人是训练前也为“优秀”的概率;
(3)跳水员A将对“5米、7.5米和10米”这三种高度进行集训,且在训练中进行了多轮测试.规定:在每轮测试中,都会有这3种高度,且至少有2个高度的跳水测试达到“优秀”,则该轮测试才记为“优秀”.每轮测试中,跳水员在每个高度中达到“优秀”的概率均为,每个高度互不影响且每轮测试互不影响.如果跳水员在集训测试中要想获得“优秀”的次数平均值达到3次,那么理论上至少要进行多少轮测试?
附:,其中.
0.05 0.01 0.005 0.001
3.841 6.635 7.879 10.828
18.已知函数,,.
(1)当时,讨论的单调性;
(2)若曲线在点处的切线与曲线也相切,求实数a的值;
(3)若不等式对任意的恒成立,求a的取值范围.为自然对数的底数)
19.椭圆的左右焦点为和,O为椭圆的中心,过作直线、,分别交椭圆C于A、B和C、D,且的最大值为,的最小值为.
(1)求椭圆C的方程;
(2)设线段、的中点分别为M、N,记的面积为,的面积为,若直线、的斜率为、且,求证:为定值,并求出这个定值.
参考答案
1.答案:A
解析:命题,的否定为:,.
故选:A.
2.答案:C
解析:因为,故.
①当时,,则,与元素的互异性矛盾,故不成立;
②当时,解得,与元素的互异性矛盾,故不成立;
③当时,即,则,,故成立,故.
故选:C.
3.答案:D
解析:设,
所以,解得,所以;
又,,所以,
故选:D.
4.答案:C
解析:由题意知回归方程为过点,则,
即;
又,,
由于回归方程为必过样本中心点,
故,
故选:C.
5.答案:D
解析:对于A,当,时,,故A错误;
对于B,因为,,所以,又,,故,
从而,故B错误;
对于C,,
因为,所以,故,
故,故C错误;
对于D,
,
因为,故,
所以,即,故D正确.
故选:D.
6.答案:C
解析:因为为偶函数,故,
又因为,且,故,则.
故,又在上单调递减,
则,即.
故.
故选:C.
7.答案:A
解析:,其中,,
当时为有理项,故有5项有理项,4项无理项,
故,,故.
故选:A.
8.答案:C
解析:由题可知:(当且仅当时取等),
化简可得,解得.
9.答案:ABC
解析:A选项,根据正态分布的定义得,故A正确;
B选项,,,故,故B正确;
C选项,,,故,故C正确;
D选项,,故D错误.
故选:ABC.
10.答案:AB
解析:由题,恒成立,易知时不满足,
时,有.
故选:AB.
11.答案:AD
解析:对于A,令,则,(其中),
故,解得,
即,所以函数的最小值为0,所以A正确,
对于B,当时,由,得,解得,所以B错误,
对于CD,由题可知,,,即对,,
令,当时,取得最小值,
即,所以,所以C错误,D正确,
故选:AD
12.答案:
解析:由题意得,解得,
所以函数的定义域为,
故答案为:.
13.答案:36
解析:若甲乙选的景点没有其他人选,则分组方式为:1,2,2的选法总数为:,
若甲乙选的景点还有其他人选择,则分组方式为:1,1,3的选法总数为:,
所以不同的选法总数为:.
故答案为:36.
14.答案:2021
解析:令,则,令,
则,解得或.
而,故.因此.则,
即.
因此或,当时,,
在上单调递减,不满足题意,舍去;当时,满足题意.则.
15.答案:(1)
(2)
解析:(1)设等差数列的公差为d,则,
解得,故;
(2)由(1)可得,
故
.
16.答案:(1),
(2)分布列见解析,万元
解析:(1)计算得,,
所以,
,
则回归直线方程为,代入得,
所以预测2024年1月新能源渗透率为;
(2)由题意,每个客户购买新能源车的概率为,燃油车概率为,
X所有可能取值为0,2,4,6,
则,
,
,
,
所以X的分布列为
X 0 2 4 6
P
所以(万元).
17.答案:(1)列联表见解析,有关,原因见解析
(2)
(3)12轮
解析:(1)零假设:假设跳水员的优秀情况与训练无关.
列联表为:
优秀人数 非优秀人数 合计
训练前 2 8 10
训练后 8 2 10
合计 10 10 20
,
故根据小概率值的独立性检验,零假设不成立,即跳水员的优秀情况与训练有关,此推断犯错误的概率不超过0.01.
(2)由图可知:训练前后均不优秀的有C,F共2人,训练前后均优秀的有D,G共2人,训练前不优秀而训练后优秀的有6人,
设“所选3人中恰有2人训练后为优秀”,“所选3人中恰有1人训练前为优秀”,
则,,
(3)设跳水员A每轮测试为优秀的概率为P,则.
设A测试次数为n,则优秀的次数,
故,
故至少需进行12轮测试.
18.答案:(1)答案见解析
(2)
(3)
解析:(1)因为,,
所以,
当时,,在上单调递增;
当时,在上单调递减;
当时,令,则,
当时,,单调递减;
当时,,单调递增;
综上:当时,在上单调递增;
当时,在单调递减,在单调递增;
当时,在上单调递减;
(2)函数,,
所以,,,
故曲线在点处的切线方程为,
即.
设切线与曲线切于点,
则,
解得.
(3)法一:函数,定义域为,
故,
等价于,
记,,
令,,
解得,,解得,
故在上单调递减,在上单调递增,
所以当时,.
所以解得,,解得,
故在单调递减,在单调递增,
有,
所以a的取值范围为.
法二:取,由,得.
下证:当时,恒成立.
记,
因,函数在单调递减,
所以,
记,,
,,
记,,
,解得,,解得,
故在单调递减,在单调递增,
故,
故,在上单调递增,即在上单调递增,
又,
在上恒成立,在恒成立,
所以在单调递减,在单调递增,
所以,得证.
综上知,a的取值范围为.
19.答案:(1)
(2)证明见解析,
解析:(1)由已知得当在x轴上时,,
当在x轴上时,最小,此时直线方程为:,
联立,解得,所以,所以,,
故椭圆方程为.
(2)由(1)得,,设直线,,
其中,,则.
由消去x得:,,
设,,,则,,
,,
即,用代换同理可得,
解法一:设直线的斜率为k,
则.
故直线的方程为,
即,
将代入得,故直线恒过定点,
于是点O与点到直线的距离之比等于,从而.
解法二:对于一个,若,,则,
证明如下:
因为,
所以,
所以,
所以;
故对于,,
所以,
又,,
则,
所以.
同课章节目录
