人教版数学九年级上册 专项练习七 22.3实际问题与二次函数(无答案)
文档属性
| 名称 | 人教版数学九年级上册 专项练习七 22.3实际问题与二次函数(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 249.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-02 00:00:00 | ||
图片预览

文档简介
专项练习七 实际问题与二次函数
一、选择题
1.已知 那么函数 6的最大值是( )
A.-6 B.—2.5
C.2 D.不能确定
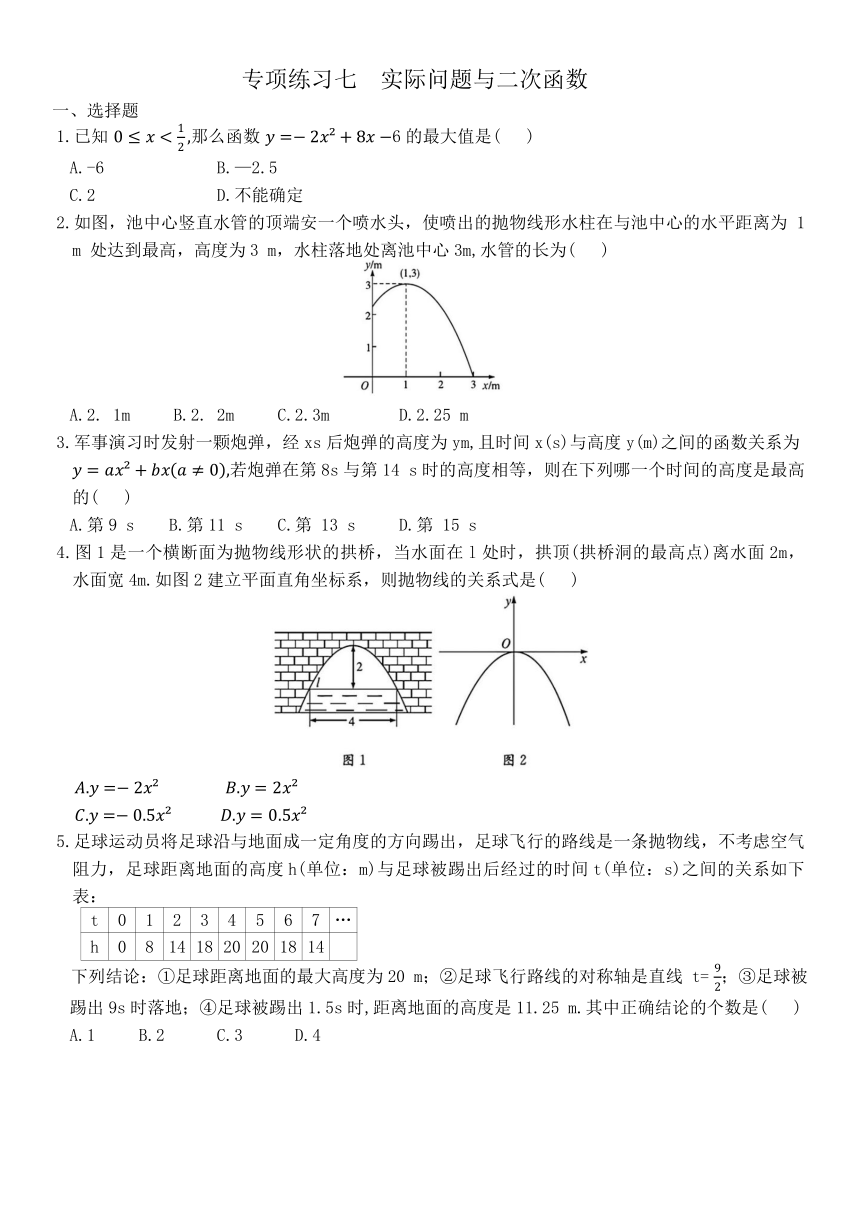
2.如图,池中心竖直水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为 1m 处达到最高,高度为3 m,水柱落地处离池中心3m,水管的长为( )
A.2. 1m B.2. 2m C.2.3m D.2.25 m
3.军事演习时发射一颗炮弹,经xs后炮弹的高度为ym,且时间x(s)与高度y(m)之间的函数关系为 若炮弹在第8s与第14 s时的高度相等,则在下列哪一个时间的高度是最高的( )
A.第9 s B.第11 s C.第 13 s D.第 15 s
4.图1是一个横断面为抛物线形状的拱桥,当水面在l处时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图2建立平面直角坐标系,则抛物线的关系式是( )
5.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14
下列结论:①足球距离地面的最大高度为20 m;②足球飞行路线的对称轴是直线 t= ;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11.25 m.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
6.小王结婚时,在小区门口的平地上放置了一个充气婚庆拱门,其形状如图所示,若将该拱门(拱门的宽度忽略不计)放在平面直角坐标系中,点 A 的坐标为(1,0).若将该拱门看作是抛物线 y= 的一部分,则点 A 与点 B的距离为( )
A.4 B.5 C.6 D.7
二、填空题
7.把一根长100m的铁丝分为两部分,每一部分均弯曲成一个正方形,它们的面积和的最小值是 cm .
8.有一种产品的质量要求从低到高分为1,2,3,4共四种不同的档次.若工时不变,车间每天可生产最低档次(即第一档次)的产品40件,生产每件产品的利润为16元;如果每提高一个档次,每件产品利润可增加1元,但每天少生产 2件产品.现在车间计划只生产一种档次的产品.要使利润最大,车间应生产第 种档次的产品.
9.飞机着陆后滑行的距离s(单位:米)关于滑行的时间t(单位:秒)的函数解析式是 s= 则飞机着陆后滑行的最长时间为 秒.
10.如图所示,一位运动员在离篮下 4 米水平距离处起跳投篮,球运行的路线是抛物线,当球运行的水平距离是2.5 米时,球达到最大高度3.5 米.已知篮筐中心到地面的距离为3.05米,问球出手时离地面 米时才能投中.
三、解答题
11.如图,已知等腰直角△ABC的直角边长与正方形 DEFG 的边长均为 8 cm,EF与AC在同一条直线上,开始时点 A 与点 F 重合,让△ABC向左移动,运动速度为 1 cm/s,最后点 A 与点 E重合.
(1)试写出两图形重叠部分的面积y(cm )与△ABC的运动时间x(s)之间的关系式;
(2)当点 A 向左运动2.5s时,重叠部分的面积是多少
12.某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是 50 件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于 75元.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数解析式;
(2)求出销售单价为多少元时,每天的销售利润最大 最大利润是多少
(3)如果该企业要使每天的销售利润不低于4 000元,那么每天的总成本至少需要多少元 (每天的总成本=每件的成本×每天的销售量)
一、选择题
1.已知 那么函数 6的最大值是( )
A.-6 B.—2.5
C.2 D.不能确定
2.如图,池中心竖直水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为 1m 处达到最高,高度为3 m,水柱落地处离池中心3m,水管的长为( )
A.2. 1m B.2. 2m C.2.3m D.2.25 m
3.军事演习时发射一颗炮弹,经xs后炮弹的高度为ym,且时间x(s)与高度y(m)之间的函数关系为 若炮弹在第8s与第14 s时的高度相等,则在下列哪一个时间的高度是最高的( )
A.第9 s B.第11 s C.第 13 s D.第 15 s
4.图1是一个横断面为抛物线形状的拱桥,当水面在l处时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图2建立平面直角坐标系,则抛物线的关系式是( )
5.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14
下列结论:①足球距离地面的最大高度为20 m;②足球飞行路线的对称轴是直线 t= ;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11.25 m.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
6.小王结婚时,在小区门口的平地上放置了一个充气婚庆拱门,其形状如图所示,若将该拱门(拱门的宽度忽略不计)放在平面直角坐标系中,点 A 的坐标为(1,0).若将该拱门看作是抛物线 y= 的一部分,则点 A 与点 B的距离为( )
A.4 B.5 C.6 D.7
二、填空题
7.把一根长100m的铁丝分为两部分,每一部分均弯曲成一个正方形,它们的面积和的最小值是 cm .
8.有一种产品的质量要求从低到高分为1,2,3,4共四种不同的档次.若工时不变,车间每天可生产最低档次(即第一档次)的产品40件,生产每件产品的利润为16元;如果每提高一个档次,每件产品利润可增加1元,但每天少生产 2件产品.现在车间计划只生产一种档次的产品.要使利润最大,车间应生产第 种档次的产品.
9.飞机着陆后滑行的距离s(单位:米)关于滑行的时间t(单位:秒)的函数解析式是 s= 则飞机着陆后滑行的最长时间为 秒.
10.如图所示,一位运动员在离篮下 4 米水平距离处起跳投篮,球运行的路线是抛物线,当球运行的水平距离是2.5 米时,球达到最大高度3.5 米.已知篮筐中心到地面的距离为3.05米,问球出手时离地面 米时才能投中.
三、解答题
11.如图,已知等腰直角△ABC的直角边长与正方形 DEFG 的边长均为 8 cm,EF与AC在同一条直线上,开始时点 A 与点 F 重合,让△ABC向左移动,运动速度为 1 cm/s,最后点 A 与点 E重合.
(1)试写出两图形重叠部分的面积y(cm )与△ABC的运动时间x(s)之间的关系式;
(2)当点 A 向左运动2.5s时,重叠部分的面积是多少
12.某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是 50 件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于 75元.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数解析式;
(2)求出销售单价为多少元时,每天的销售利润最大 最大利润是多少
(3)如果该企业要使每天的销售利润不低于4 000元,那么每天的总成本至少需要多少元 (每天的总成本=每件的成本×每天的销售量)
同课章节目录
