人教版数学九年级上册 专题集训二 第22章 二次函数综合训练(无答案)
文档属性
| 名称 | 人教版数学九年级上册 专题集训二 第22章 二次函数综合训练(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 391.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-02 00:00:00 | ||
图片预览

文档简介
专题集训二 二次函数
(满分120分,时间120分钟)
题号 一 二 三 总分
得分
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.下列各式中,是二次函数的是( )
A. y=-2x+1
2.对于二次函数 和 下列说法中正确的是( )
A.开口都向上,且都关于y轴对称 B.开口都向上,且都关于x轴对称
C.顶点都是原点,且都关于y轴对称 D.顶点都是原点,且都关于x轴对称
3.抛物线 的顶点坐标是( )
A.(1,0) B.(-1,0) C.(-2,1) D.(2,-1)
4.若(-3,y ),(-2,y ),(1,y )为二次函数. 的图象上的三点,则y ,y ,y 的大小关系是( )
5.已知抛物线 与x轴交点的横坐标的和为-4,积是-5,且抛物线经过点(0,-5),则此抛物线的解析式为( )
6.已知函数. 的图象与x轴有交点,则k的取值范围是( )
A. k≤4,且k≠3 B. k<4,且k≠3 C. k<4 D. k≤4
7.用长40m的篱笆围成一个矩形菜园,则围成的菜园的最大面积为( )
8.在直角坐标系xOy中,二次函数C ,C 图象上部分点的横坐标、纵坐标间的对应值如下表:
x --1 0 1 2 2.5 3 4
y 0 m -8 n -8.75 --8 -5
y 5 m -11 n2 -12.5 -11 --5
则关于它们图象的结论正确的是( )
A.图象 C ,C 均开口向下 B.图象 C 的顶点坐标为(2.5,—8.75)
C.当x>4时,y >y D.图象 C ,C 必经过定点(0,—5)
9.抛物线 开口向下,与x轴两个交点的横坐标分别为—1和 3,则下列结论正确的是( )
A. abc>0 D. a-b+c=0
10.便民超市的小王对该超市苹果的销售进行了统计,某进价为2元/千克的苹果每天的销售量y(千克)和当天的售价x(元/千克)之间满足 y=-20x+200(3≤x≤5),,若要使该品种苹果当天的利润达到最高,则其售价应为[利润=销售量·(售价-进价)]( )
A.5元 B.4元 C.3.5元 D.3元
二、填空题(本大题共8小题,每小题4分,共32分.本题要求把正确结果填在规定的横线上,不需要解答过程)
11.两个正方形的周长之和为20cm,其中一个正方形的边长是xcm,则这两个正方形的面积之和 y(cm )与x(cm)的函数关系式为 .
12.二次函数 的图象先向右平移2个单位,再向下平移3个单位后,所得抛物线的解析式为
13.若抛物线 的图象最高点的纵坐标为0,则m的值为 .
14.抛物线和 形状相同,方向相反,且顶点为(-1,3),则它的解析式为 .
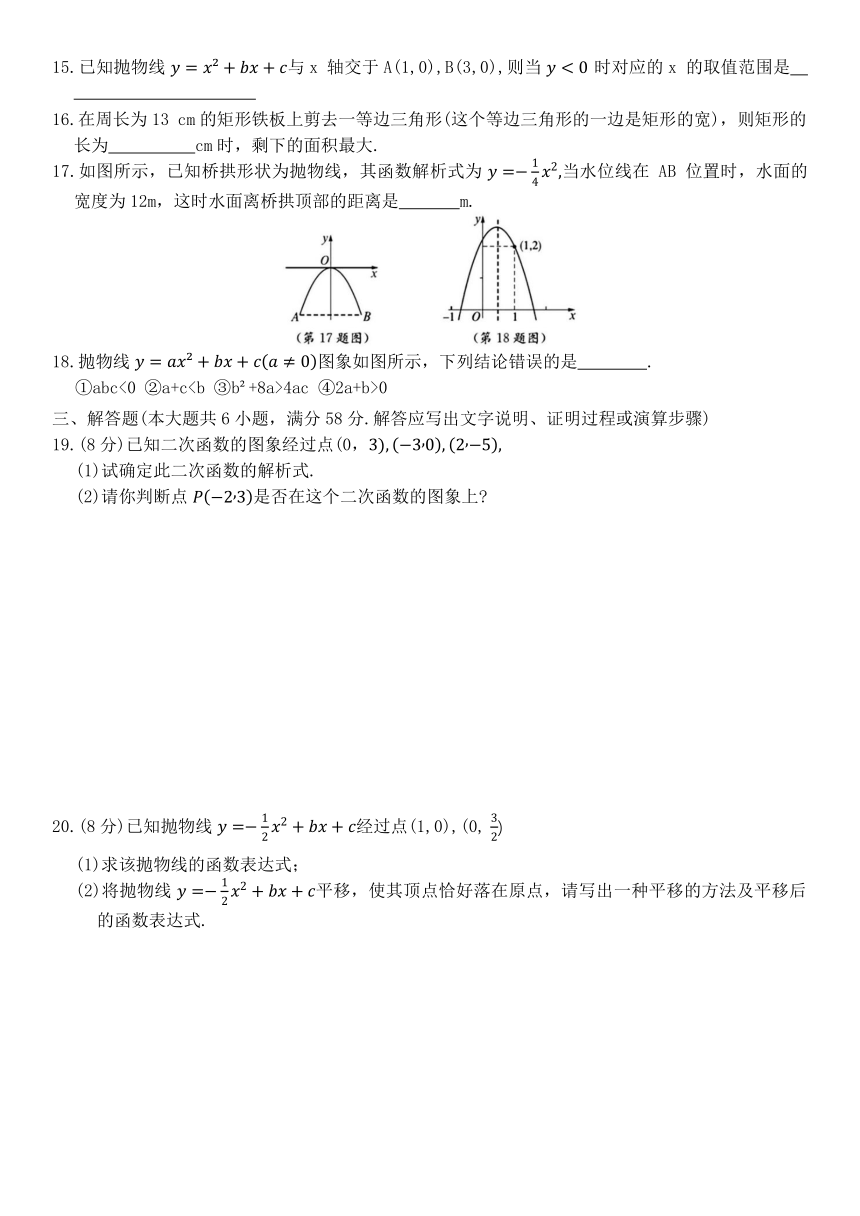
15.已知抛物线 与x 轴交于A(1,0),B(3,0),则当 时对应的x 的取值范围是
16.在周长为13 cm的矩形铁板上剪去一等边三角形(这个等边三角形的一边是矩形的宽),则矩形的长为 cm时,剩下的面积最大.
17.如图所示,已知桥拱形状为抛物线,其函数解析式为 当水位线在 AB 位置时,水面的宽度为12m,这时水面离桥拱顶部的距离是 m.
18.抛物线 图象如图所示,下列结论错误的是 .
①abc<0 ②a+c4ac ④2a+b>0
三、解答题(本大题共6小题,满分58分.解答应写出文字说明、证明过程或演算步骤)
19.(8分)已知二次函数的图象经过点(0,
(1)试确定此二次函数的解析式.
(2)请你判断点 是否在这个二次函数的图象上
20.(8分)已知抛物线 经过点(1,0),(0, )
(1)求该抛物线的函数表达式;
(2)将抛物线 平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.
21.(10分)某商店原来将进货价为8元/件的商品按10元/件售出,每天可销售200件.现在采用提高售价,减少进货量的方法来增加利润,已知每件商品涨价 1元,每天的销售量就减少20 件.设这种商品每件涨价x元.
(1)填空:原来每件商品的利润是 元,涨价后每件商品的实际利润是 元(可用含x的代数式表示).
(2)为了使每天获得700元的利润,售价应定为多少元
(3)售价定为多少元时,每天利润最大,最大利润是多少元
22.(10分)已知直线l 与抛物线
(1)求证:直线l与该抛物线总有两个交点;
(2)设直线l与该抛物线两交点为A,B,O为原点,当 时,求 的面积.
23.(10分)某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为x轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.
24.(12分)如图1,抛物线 与x轴交于点A 和点B(1,0),与y轴交于点 抛物线y 的顶点为G, 轴于点M.将抛物线y 平移后得到顶点为B且对称轴为直l的抛物线y
(1)求抛物线. 的解析式;
(2)如图2,在直线l上是否存在点T,使 是等腰三角形 若存在,请求出所有点 T的坐标:若不存在,请说明理由;
(3)点 P 为抛物线. 上一动点,过点 P 作y轴的平行线交抛物线y 于点 Q点Q 关于直线l 的对称点为R 若以 P,Q,R 为顶点的三角形与 全等,求直线 PR 的解析式.
(满分120分,时间120分钟)
题号 一 二 三 总分
得分
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.下列各式中,是二次函数的是( )
A. y=-2x+1
2.对于二次函数 和 下列说法中正确的是( )
A.开口都向上,且都关于y轴对称 B.开口都向上,且都关于x轴对称
C.顶点都是原点,且都关于y轴对称 D.顶点都是原点,且都关于x轴对称
3.抛物线 的顶点坐标是( )
A.(1,0) B.(-1,0) C.(-2,1) D.(2,-1)
4.若(-3,y ),(-2,y ),(1,y )为二次函数. 的图象上的三点,则y ,y ,y 的大小关系是( )
5.已知抛物线 与x轴交点的横坐标的和为-4,积是-5,且抛物线经过点(0,-5),则此抛物线的解析式为( )
6.已知函数. 的图象与x轴有交点,则k的取值范围是( )
A. k≤4,且k≠3 B. k<4,且k≠3 C. k<4 D. k≤4
7.用长40m的篱笆围成一个矩形菜园,则围成的菜园的最大面积为( )
8.在直角坐标系xOy中,二次函数C ,C 图象上部分点的横坐标、纵坐标间的对应值如下表:
x --1 0 1 2 2.5 3 4
y 0 m -8 n -8.75 --8 -5
y 5 m -11 n2 -12.5 -11 --5
则关于它们图象的结论正确的是( )
A.图象 C ,C 均开口向下 B.图象 C 的顶点坐标为(2.5,—8.75)
C.当x>4时,y >y D.图象 C ,C 必经过定点(0,—5)
9.抛物线 开口向下,与x轴两个交点的横坐标分别为—1和 3,则下列结论正确的是( )
A. abc>0 D. a-b+c=0
10.便民超市的小王对该超市苹果的销售进行了统计,某进价为2元/千克的苹果每天的销售量y(千克)和当天的售价x(元/千克)之间满足 y=-20x+200(3≤x≤5),,若要使该品种苹果当天的利润达到最高,则其售价应为[利润=销售量·(售价-进价)]( )
A.5元 B.4元 C.3.5元 D.3元
二、填空题(本大题共8小题,每小题4分,共32分.本题要求把正确结果填在规定的横线上,不需要解答过程)
11.两个正方形的周长之和为20cm,其中一个正方形的边长是xcm,则这两个正方形的面积之和 y(cm )与x(cm)的函数关系式为 .
12.二次函数 的图象先向右平移2个单位,再向下平移3个单位后,所得抛物线的解析式为
13.若抛物线 的图象最高点的纵坐标为0,则m的值为 .
14.抛物线和 形状相同,方向相反,且顶点为(-1,3),则它的解析式为 .
15.已知抛物线 与x 轴交于A(1,0),B(3,0),则当 时对应的x 的取值范围是
16.在周长为13 cm的矩形铁板上剪去一等边三角形(这个等边三角形的一边是矩形的宽),则矩形的长为 cm时,剩下的面积最大.
17.如图所示,已知桥拱形状为抛物线,其函数解析式为 当水位线在 AB 位置时,水面的宽度为12m,这时水面离桥拱顶部的距离是 m.
18.抛物线 图象如图所示,下列结论错误的是 .
①abc<0 ②a+c4ac ④2a+b>0
三、解答题(本大题共6小题,满分58分.解答应写出文字说明、证明过程或演算步骤)
19.(8分)已知二次函数的图象经过点(0,
(1)试确定此二次函数的解析式.
(2)请你判断点 是否在这个二次函数的图象上
20.(8分)已知抛物线 经过点(1,0),(0, )
(1)求该抛物线的函数表达式;
(2)将抛物线 平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.
21.(10分)某商店原来将进货价为8元/件的商品按10元/件售出,每天可销售200件.现在采用提高售价,减少进货量的方法来增加利润,已知每件商品涨价 1元,每天的销售量就减少20 件.设这种商品每件涨价x元.
(1)填空:原来每件商品的利润是 元,涨价后每件商品的实际利润是 元(可用含x的代数式表示).
(2)为了使每天获得700元的利润,售价应定为多少元
(3)售价定为多少元时,每天利润最大,最大利润是多少元
22.(10分)已知直线l 与抛物线
(1)求证:直线l与该抛物线总有两个交点;
(2)设直线l与该抛物线两交点为A,B,O为原点,当 时,求 的面积.
23.(10分)某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为x轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.
24.(12分)如图1,抛物线 与x轴交于点A 和点B(1,0),与y轴交于点 抛物线y 的顶点为G, 轴于点M.将抛物线y 平移后得到顶点为B且对称轴为直l的抛物线y
(1)求抛物线. 的解析式;
(2)如图2,在直线l上是否存在点T,使 是等腰三角形 若存在,请求出所有点 T的坐标:若不存在,请说明理由;
(3)点 P 为抛物线. 上一动点,过点 P 作y轴的平行线交抛物线y 于点 Q点Q 关于直线l 的对称点为R 若以 P,Q,R 为顶点的三角形与 全等,求直线 PR 的解析式.
同课章节目录
