1.1.1 空间向量及其运算 课件(共32张PPT) -2023-2024学年高二数学同步课堂(人教B版2019选择性必修第一册)
文档属性
| 名称 | 1.1.1 空间向量及其运算 课件(共32张PPT) -2023-2024学年高二数学同步课堂(人教B版2019选择性必修第一册) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-04 00:00:00 | ||
图片预览





文档简介
(共32张PPT)
1.1.1 空间向量及其运算
目录
学习任务
思维导图
复习引入
主体学习
课堂小结
学习任务
PART ONE
1.了解空间向量的概念.
2.理解空间向量的加、减运算.
3.理解空间向量的数乘运算.
4.理解空间向量的数量积运算.
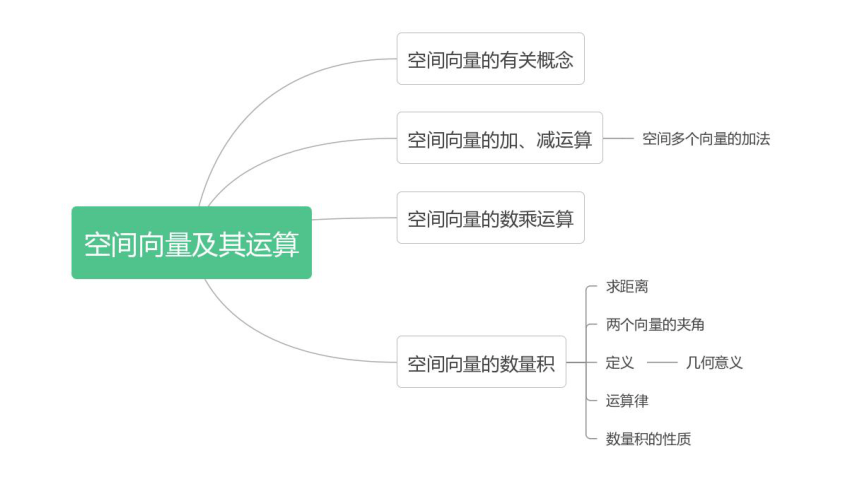
思维导图
PART TWO
复习引入
PART THREE
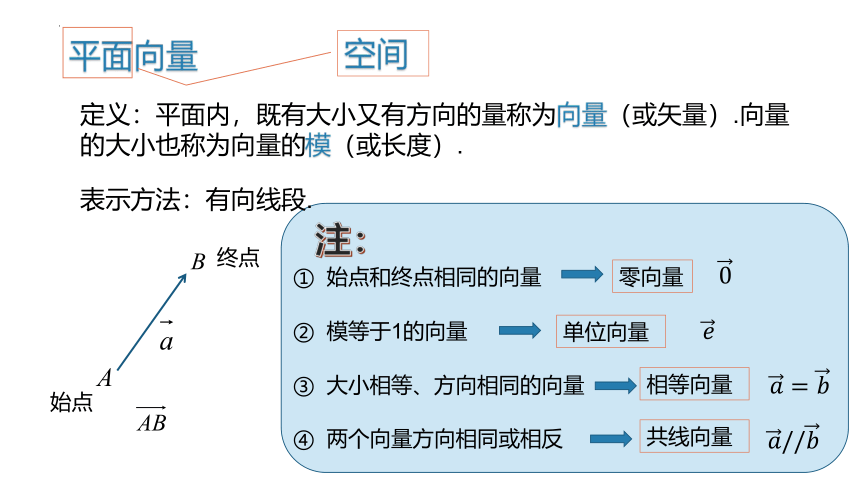
平面向量
定义:平面内,既有大小又有方向的量称为向量(或矢量).向量的大小也称为向量的模(或长度).
表示方法:有向线段.
始点
终点
① 始点和终点相同的向量
零向量
注:
② 模等于1的向量
单位向量
③ 大小相等、方向相同的向量
相等向量
④ 两个向量方向相同或相反
共线向量
空间
主体学习
PART FOUR
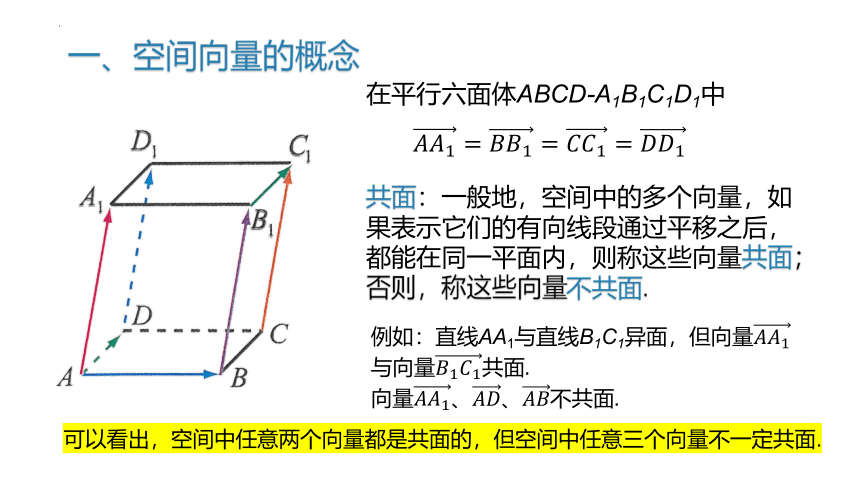
一、空间向量的概念
在平行六面体ABCD-A1B1C1D1中
共面:一般地,空间中的多个向量,如果表示它们的有向线段通过平移之后,都能在同一平面内,则称这些向量共面;否则,称这些向量不共面.
例如:直线AA1与直线B1C1异面,但向量与向量共面.
向量、、不共面.
可以看出,空间中任意两个向量都是共面的,但空间中任意三个向量不一定共面.
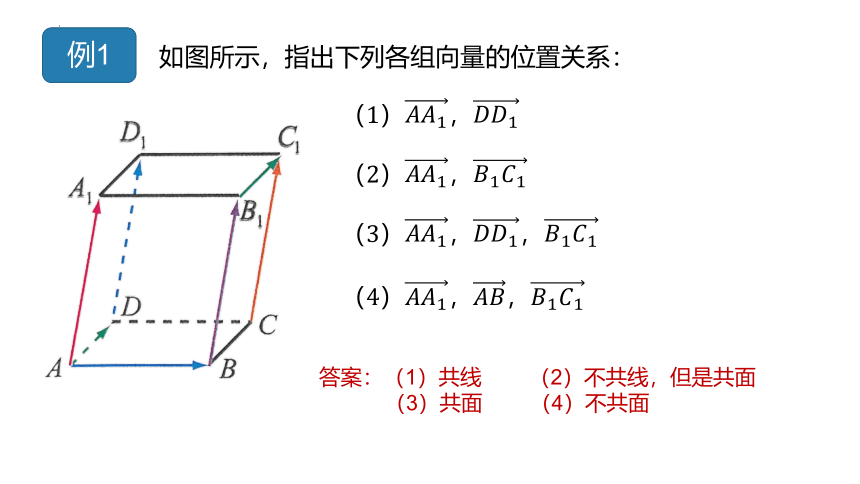
例1
如图所示,指出下列各组向量的位置关系:
,
,
,,
,,
答案:(1)共线 (2)不共线,但是共面
(3)共面 (4)不共面
空间向量可以用来描述空间中既有大小又有方向的量.例如,当空间中的物体所受的力不全在同一个平面内时,可以借助空间向量来对该物体进行受力分析,如图所示是吊在空间中的物体所受力的示意图.
二、空间向量的加法运算
平面向量的加法:
三角形法则
平行四边形法则
空间任意两个向量共面,故空间中两个向量的和与平面内的情形完全一样.
例2
求下列向量的和:
(1)
(2)
答案:(1) (2)
空间向量的加法也满足交换律和结合律
解:
例3
如图所示平行六面体ABCD-A1B1C1D1,
化简
例3说明:三个不共面的向量的和,等于以这三个向量为邻边的平行六面体中,与这三个向量有共同始点的体对角线所表示的向量.
三、空间向量的线性运算
向量的减法:
数乘向量:
三角形法则
任意两个空间向量共面,故空间中两个向量的运算与平面内的情形完全一样.
(1)当且时,的模为|,而且的方向:
①当时,与的方向相同;
②当时,与的方向相反.
(2)当=0或时,=.
例4
设AB是空间中任意一条线段,O是空间中任意一点,求证:M为AB中点的充要条件是
如图所示,如果棱锥O-ABCD的底面ABCD是一个平行四边形,则N既是AC的中点,也是BD的中点
例5
如图所示三棱锥A-BCD中,O为CD的中点,化简
练
如图所示,M,N分别是四面体ABCD的棱AB,CD的中点,求证:.
即是
四、空间向量的数量积
1. 两个向量的夹角
任意两个空间向量共面,故空间中两个向量的夹角与平面内的情形完全一样.
例6
如图所示是一个正方体,求下列各对向量的夹角:
2. 向量的数量积
3.向量的投影与向量数量积的几何意义
可以是正数、负数或0.
空间向量同理.
3.向量数量积的性质
例7
如图所示长方体ABCD-A’B’C’D’中,E是AA’的中点,AA’=AD=2,AB=4,求:
课堂小结
PART FIVE
谢谢观看
1.1.1 空间向量及其运算
目录
学习任务
思维导图
复习引入
主体学习
课堂小结
学习任务
PART ONE
1.了解空间向量的概念.
2.理解空间向量的加、减运算.
3.理解空间向量的数乘运算.
4.理解空间向量的数量积运算.
思维导图
PART TWO
复习引入
PART THREE
平面向量
定义:平面内,既有大小又有方向的量称为向量(或矢量).向量的大小也称为向量的模(或长度).
表示方法:有向线段.
始点
终点
① 始点和终点相同的向量
零向量
注:
② 模等于1的向量
单位向量
③ 大小相等、方向相同的向量
相等向量
④ 两个向量方向相同或相反
共线向量
空间
主体学习
PART FOUR
一、空间向量的概念
在平行六面体ABCD-A1B1C1D1中
共面:一般地,空间中的多个向量,如果表示它们的有向线段通过平移之后,都能在同一平面内,则称这些向量共面;否则,称这些向量不共面.
例如:直线AA1与直线B1C1异面,但向量与向量共面.
向量、、不共面.
可以看出,空间中任意两个向量都是共面的,但空间中任意三个向量不一定共面.
例1
如图所示,指出下列各组向量的位置关系:
,
,
,,
,,
答案:(1)共线 (2)不共线,但是共面
(3)共面 (4)不共面
空间向量可以用来描述空间中既有大小又有方向的量.例如,当空间中的物体所受的力不全在同一个平面内时,可以借助空间向量来对该物体进行受力分析,如图所示是吊在空间中的物体所受力的示意图.
二、空间向量的加法运算
平面向量的加法:
三角形法则
平行四边形法则
空间任意两个向量共面,故空间中两个向量的和与平面内的情形完全一样.
例2
求下列向量的和:
(1)
(2)
答案:(1) (2)
空间向量的加法也满足交换律和结合律
解:
例3
如图所示平行六面体ABCD-A1B1C1D1,
化简
例3说明:三个不共面的向量的和,等于以这三个向量为邻边的平行六面体中,与这三个向量有共同始点的体对角线所表示的向量.
三、空间向量的线性运算
向量的减法:
数乘向量:
三角形法则
任意两个空间向量共面,故空间中两个向量的运算与平面内的情形完全一样.
(1)当且时,的模为|,而且的方向:
①当时,与的方向相同;
②当时,与的方向相反.
(2)当=0或时,=.
例4
设AB是空间中任意一条线段,O是空间中任意一点,求证:M为AB中点的充要条件是
如图所示,如果棱锥O-ABCD的底面ABCD是一个平行四边形,则N既是AC的中点,也是BD的中点
例5
如图所示三棱锥A-BCD中,O为CD的中点,化简
练
如图所示,M,N分别是四面体ABCD的棱AB,CD的中点,求证:.
即是
四、空间向量的数量积
1. 两个向量的夹角
任意两个空间向量共面,故空间中两个向量的夹角与平面内的情形完全一样.
例6
如图所示是一个正方体,求下列各对向量的夹角:
2. 向量的数量积
3.向量的投影与向量数量积的几何意义
可以是正数、负数或0.
空间向量同理.
3.向量数量积的性质
例7
如图所示长方体ABCD-A’B’C’D’中,E是AA’的中点,AA’=AD=2,AB=4,求:
课堂小结
PART FIVE
谢谢观看
