12.3角的平分线的性质同步练习 人教版数学八年级上册(含答案)
文档属性
| 名称 | 12.3角的平分线的性质同步练习 人教版数学八年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 650.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-02 10:46:39 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
12.3角的平分线的性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
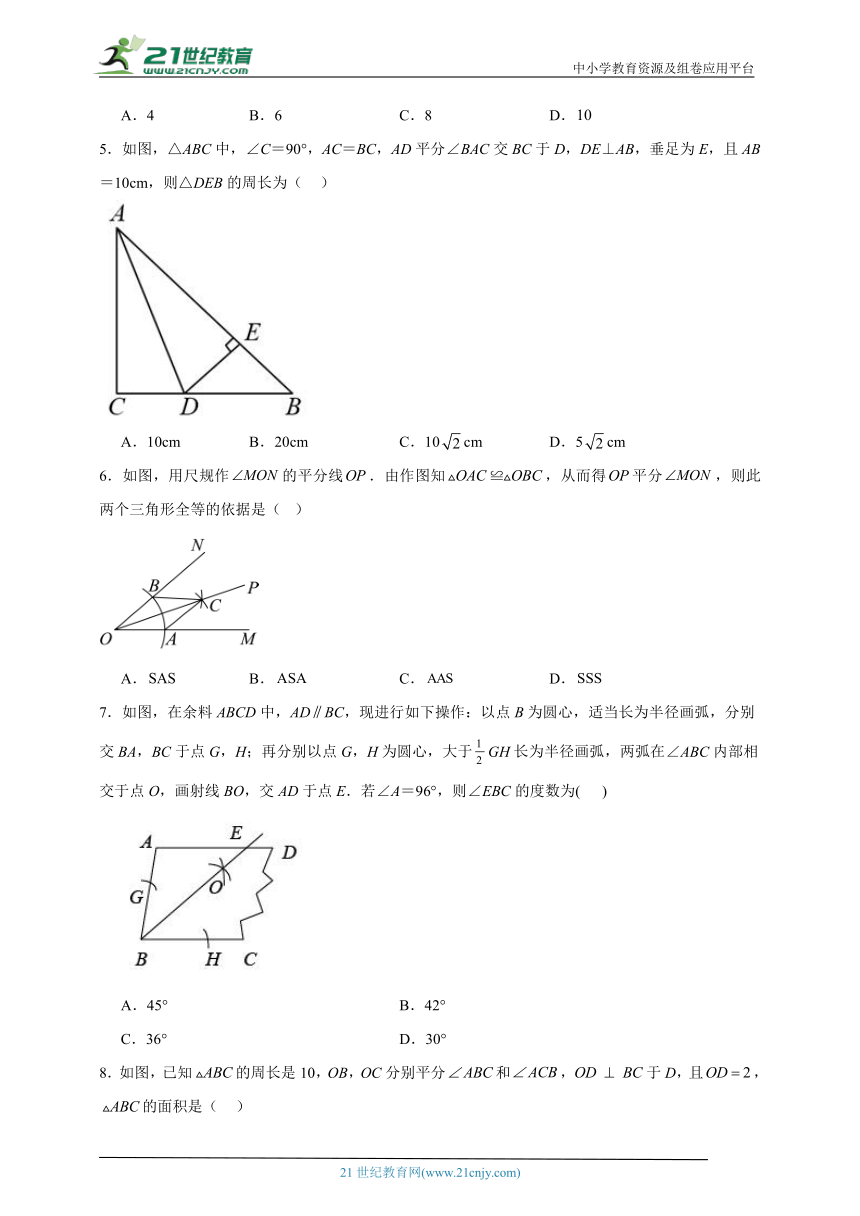
1.如图,在中,,以A为圆心,任意长为半径画弧分别,于点M和N,再分别以M,N为圆心,大于的长为半径画弧,两弧交于点P,连接AP并延长交于点D.若,则点D到的距离为( )
A.1 B.2 C.3 D.4
2.如图,在上求一点P,使它到,的距离相等,则P点是( )
A.线段的中点 B.与的中垂线的交点
C.与的平分线的交点 D.与的中垂线的交点
3.如图,在中,,点是、平分线的交点,且,,则点到边的距离为( )
A. B. C. D.
4.如图,在中,,是的平分线,于点E,已知,,则的长为( )
A.4 B.6 C.8 D.
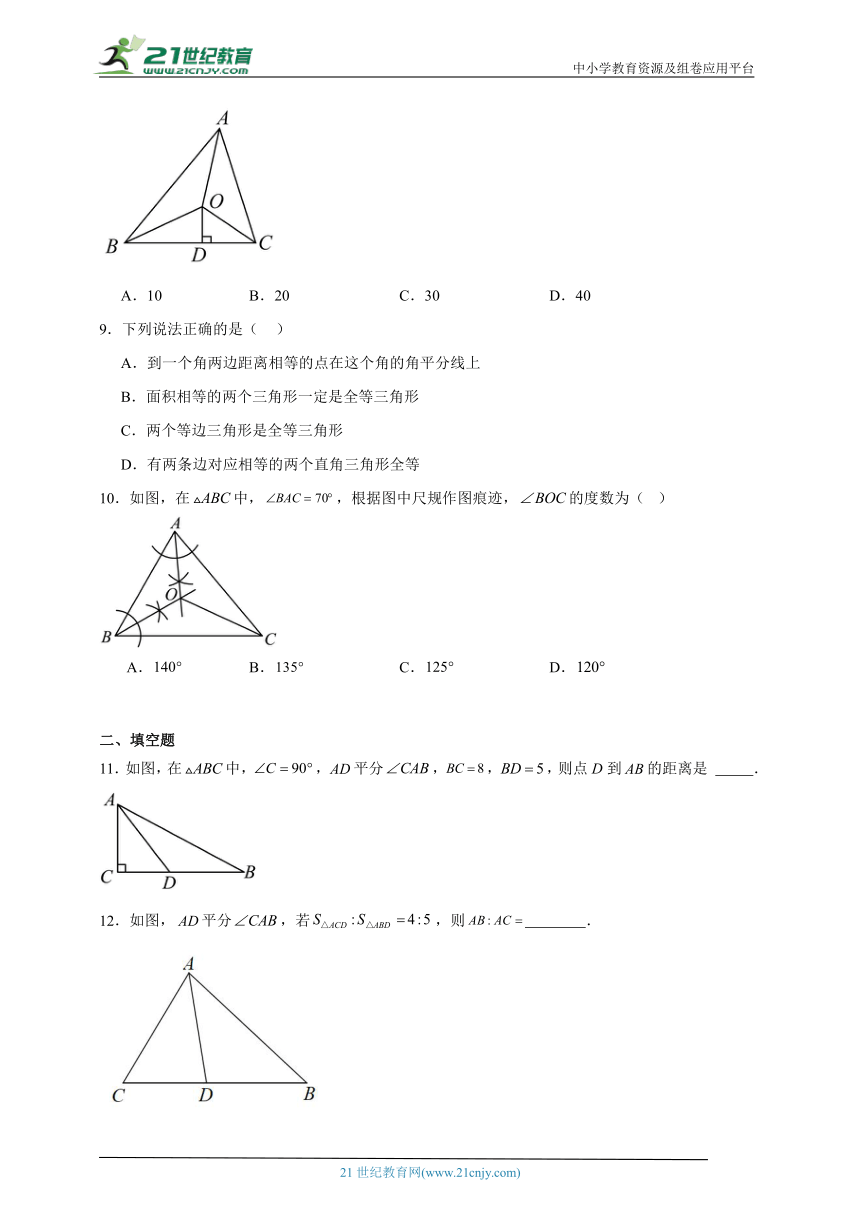
5.如图,△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB,垂足为E,且AB=10cm,则△DEB的周长为( )
A.10cm B.20cm C.10cm D.5cm
6.如图,用尺规作的平分线.由作图知,从而得平分,则此两个三角形全等的依据是( )
A. B. C. D.
7.如图,在余料ABCD中,ADBC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于GH长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.若∠A=96°,则∠EBC的度数为( )
A.45° B.42°
C.36° D.30°
8.如图,已知的周长是10,OB,OC分别平分和,于D,且,的面积是( )
A.10 B.20 C.30 D.40
9.下列说法正确的是( )
A.到一个角两边距离相等的点在这个角的角平分线上
B.面积相等的两个三角形一定是全等三角形
C.两个等边三角形是全等三角形
D.有两条边对应相等的两个直角三角形全等
10.如图,在中,,根据图中尺规作图痕迹,的度数为( )
A. B. C. D.
二、填空题
11.如图,在中,,平分,,,则点D到的距离是 .
12.如图,平分,若,则 .
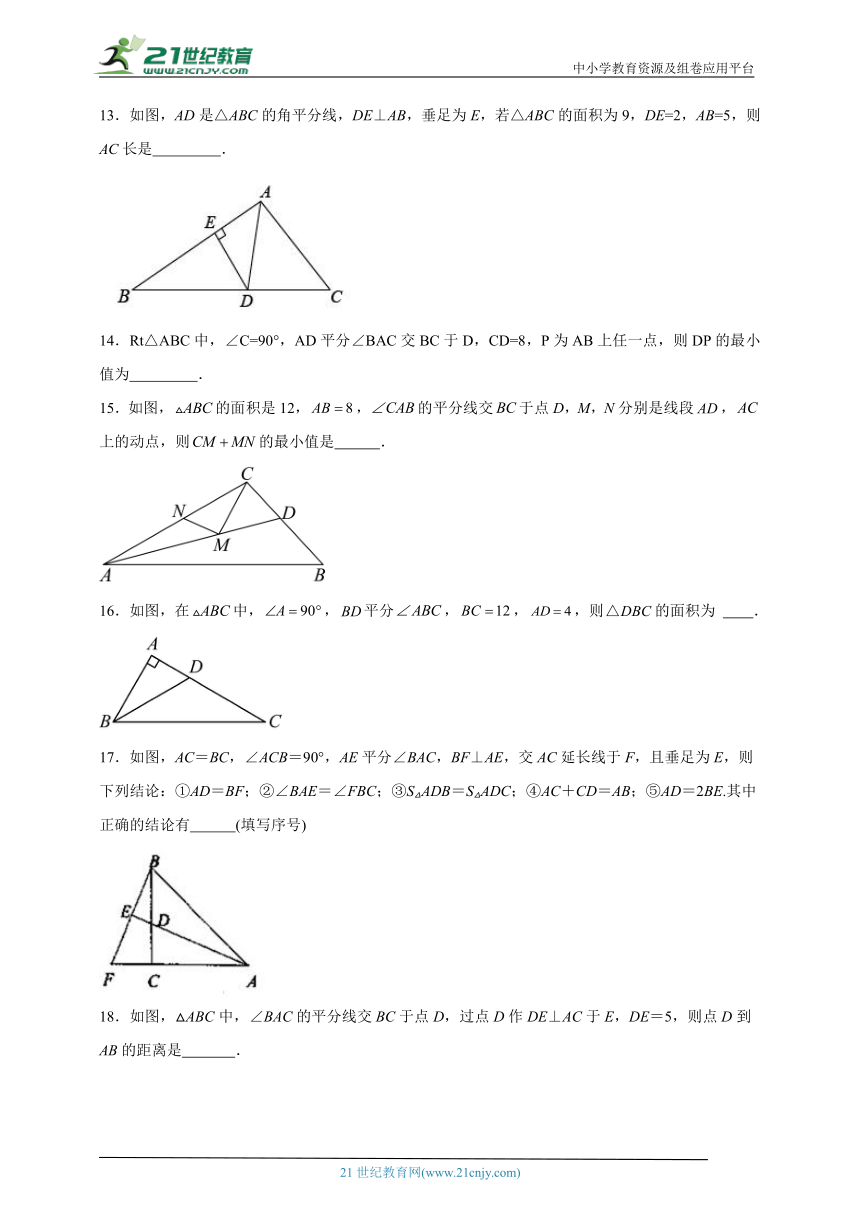
13.如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,若△ABC的面积为9,DE=2,AB=5,则AC长是 .
14.Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,CD=8,P为AB上任一点,则DP的最小值为 .
15.如图,的面积是12,,的平分线交于点D,M,N分别是线段,上的动点,则的最小值是 .
16.如图,在中,,平分,,,则的面积为 .
17.如图,AC=BC,∠ACB=90°,AE平分∠BAC,BF⊥AE,交AC延长线于F,且垂足为E,则下列结论:①AD=BF;②∠BAE=∠FBC;③S△ADB=S△ADC;④AC+CD=AB;⑤AD=2BE.其中正确的结论有 (填写序号)
18.如图,△ABC中,∠BAC的平分线交BC于点D,过点D作DE⊥AC于E,DE=5,则点D到AB的距离是 .
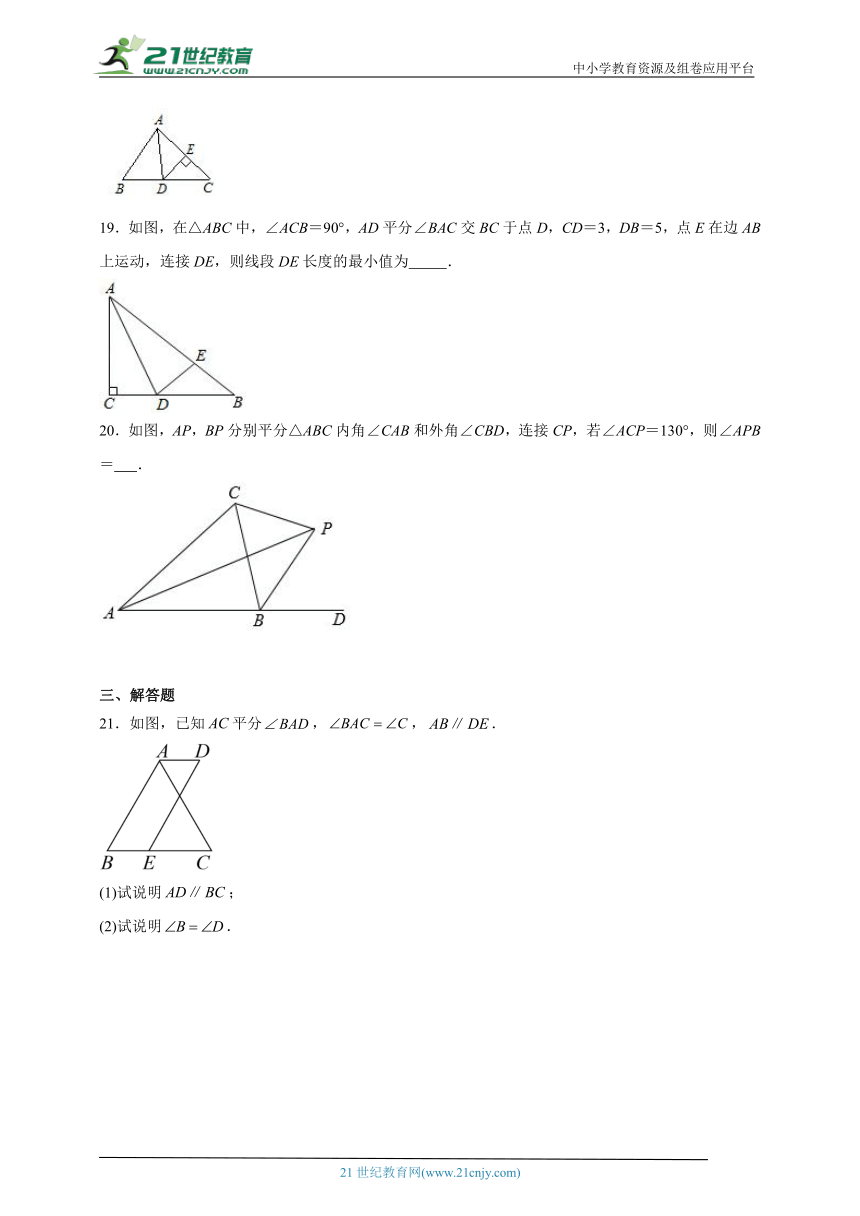
19.如图,在△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,CD=3,DB=5,点E在边AB上运动,连接DE,则线段DE长度的最小值为 .
20.如图,AP,BP分别平分△ABC内角∠CAB和外角∠CBD,连接CP,若∠ACP=130°,则∠APB= .
三、解答题
21.如图,已知平分,,.
(1)试说明;
(2)试说明.
22.如图,AB∥CD,∠BEC的平分线交CD于点F,若∠MEB=52°,求∠EFC的度数.
23.如图,已知在四边形ABCD中,AD∥BC,连接AC、BD.
(1)用基本尺规作图:作∠ACB的角平分线CM,交DA的延长线于点E,交BD于F(保留画图的痕迹,不写作法);
(2)若F是BD的中点,AD=4,AC=3,求BC的长.
24.大边对大角原理:“三角形中大角对大边,大边对大角”,该原理是几何学中的一个基本原理,通常被称为“角边关系”.在欧氏几何中,这个原理被视为公理.某数学小组对此原理进行探究并制订项目式学习表如下,请你按照思路将图形和推理过程补充完整.
课题 探究三角形中“大边对大角原理” 2024年××月××日
探究方式 利用截取法和三角形的性质进行推理
成员 组长××× 成员×××
材料 白纸、笔、直尺
命题 已知:在中,,试说明:.
图形
思路 作的角平分线,在边上取点E,使得,连接,利用全等三角形的判定及性质说明,再利用三角形的内角和定理说明
推理 因为, 所以, 所以,即.
25.如图①,在△ABC中,∠BAC=90°,AD是BC边上的高.
(1)求证:∠DAC=∠ABC;
(2)如图②,△ABC的角平分线CF交AD于点E,求证:∠AFE=∠AEF.
参考答案:
1.C
2.C
3.A
4.D
5.A
6.D
7.B
8.A
9.D
10.C
11.3
12.
13.4
14.8
15.3
16.
17.:①②④⑤.
18.5
19.3
20.
21.略
22.∠EFC =64°.
23.(1)略;(2)7
24.略
25.略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
12.3角的平分线的性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在中,,以A为圆心,任意长为半径画弧分别,于点M和N,再分别以M,N为圆心,大于的长为半径画弧,两弧交于点P,连接AP并延长交于点D.若,则点D到的距离为( )
A.1 B.2 C.3 D.4
2.如图,在上求一点P,使它到,的距离相等,则P点是( )
A.线段的中点 B.与的中垂线的交点
C.与的平分线的交点 D.与的中垂线的交点
3.如图,在中,,点是、平分线的交点,且,,则点到边的距离为( )
A. B. C. D.
4.如图,在中,,是的平分线,于点E,已知,,则的长为( )
A.4 B.6 C.8 D.
5.如图,△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB,垂足为E,且AB=10cm,则△DEB的周长为( )
A.10cm B.20cm C.10cm D.5cm
6.如图,用尺规作的平分线.由作图知,从而得平分,则此两个三角形全等的依据是( )
A. B. C. D.
7.如图,在余料ABCD中,ADBC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于GH长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.若∠A=96°,则∠EBC的度数为( )
A.45° B.42°
C.36° D.30°
8.如图,已知的周长是10,OB,OC分别平分和,于D,且,的面积是( )
A.10 B.20 C.30 D.40
9.下列说法正确的是( )
A.到一个角两边距离相等的点在这个角的角平分线上
B.面积相等的两个三角形一定是全等三角形
C.两个等边三角形是全等三角形
D.有两条边对应相等的两个直角三角形全等
10.如图,在中,,根据图中尺规作图痕迹,的度数为( )
A. B. C. D.
二、填空题
11.如图,在中,,平分,,,则点D到的距离是 .
12.如图,平分,若,则 .
13.如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,若△ABC的面积为9,DE=2,AB=5,则AC长是 .
14.Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,CD=8,P为AB上任一点,则DP的最小值为 .
15.如图,的面积是12,,的平分线交于点D,M,N分别是线段,上的动点,则的最小值是 .
16.如图,在中,,平分,,,则的面积为 .
17.如图,AC=BC,∠ACB=90°,AE平分∠BAC,BF⊥AE,交AC延长线于F,且垂足为E,则下列结论:①AD=BF;②∠BAE=∠FBC;③S△ADB=S△ADC;④AC+CD=AB;⑤AD=2BE.其中正确的结论有 (填写序号)
18.如图,△ABC中,∠BAC的平分线交BC于点D,过点D作DE⊥AC于E,DE=5,则点D到AB的距离是 .
19.如图,在△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,CD=3,DB=5,点E在边AB上运动,连接DE,则线段DE长度的最小值为 .
20.如图,AP,BP分别平分△ABC内角∠CAB和外角∠CBD,连接CP,若∠ACP=130°,则∠APB= .
三、解答题
21.如图,已知平分,,.
(1)试说明;
(2)试说明.
22.如图,AB∥CD,∠BEC的平分线交CD于点F,若∠MEB=52°,求∠EFC的度数.
23.如图,已知在四边形ABCD中,AD∥BC,连接AC、BD.
(1)用基本尺规作图:作∠ACB的角平分线CM,交DA的延长线于点E,交BD于F(保留画图的痕迹,不写作法);
(2)若F是BD的中点,AD=4,AC=3,求BC的长.
24.大边对大角原理:“三角形中大角对大边,大边对大角”,该原理是几何学中的一个基本原理,通常被称为“角边关系”.在欧氏几何中,这个原理被视为公理.某数学小组对此原理进行探究并制订项目式学习表如下,请你按照思路将图形和推理过程补充完整.
课题 探究三角形中“大边对大角原理” 2024年××月××日
探究方式 利用截取法和三角形的性质进行推理
成员 组长××× 成员×××
材料 白纸、笔、直尺
命题 已知:在中,,试说明:.
图形
思路 作的角平分线,在边上取点E,使得,连接,利用全等三角形的判定及性质说明,再利用三角形的内角和定理说明
推理 因为, 所以, 所以,即.
25.如图①,在△ABC中,∠BAC=90°,AD是BC边上的高.
(1)求证:∠DAC=∠ABC;
(2)如图②,△ABC的角平分线CF交AD于点E,求证:∠AFE=∠AEF.
参考答案:
1.C
2.C
3.A
4.D
5.A
6.D
7.B
8.A
9.D
10.C
11.3
12.
13.4
14.8
15.3
16.
17.:①②④⑤.
18.5
19.3
20.
21.略
22.∠EFC =64°.
23.(1)略;(2)7
24.略
25.略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
