2023-2024学年新疆实验中学高一(下)期末数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年新疆实验中学高一(下)期末数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 124.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-02 13:20:15 | ||
图片预览



文档简介
2023-2024学年新疆实验中学高一(下)期末数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在复平面内,复数对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.已知向量,,,若,则( )
A. B. C. D.
3.从分别写有,,,,,的张卡片中无放回地随机抽取张,则抽到的张卡片上的数字之和是的倍数的概率为( )
A. B. C. D.
4.已知一组数据为,,,,,,,,其平均数、第百分位数和众数的大小关系是( )
A. 平均数第百分位数众数 B. 平均数第百分位数众数
C. 第百分位数众数平均数 D. 平均数第百分位数众数
5.盒内有个红球,个白球,个黑球,从中任取个球,则下列选项中的两个事件互斥而不对立的是( )
A. 至少有个白球;至多有个白球 B. 至少有个白球;至少有个黑球
C. 至少有个白球;红,黑球各个 D. 至少有个白球;没有白球
6.年小明的月工资为元,各种途占比如图所示,年小明的月工资的各种用途占比如图所示,已知年小明每月的旅行费用比年增加了元,则年小明的月工资为( )
A. B. C. D.
7.天气预报说,在今后的三天中,每一天下雨的概率均为,用数字,,,表示下雨,数字,,,,,表示不下雨,由计算机产生如下组随机数:
,,,,,,,,,,
,,,,,,,,,.
由此估计今后三天中至少有一天下雨的概率为( )
A. B. C. D.
8.如图,在单位正方体中,点在线段上运动,给出以下四个命题:
异面直线与间的距离为定值;
三棱锥的体积为定值;
异面直线与直线所成的角为定值;
二面角的大小为定值.
其中真命题有( )
A. 个 B. 个 C. 个 D. 个
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.设,为两个随机事件,以下命题正确的为( )
A. 若,是互斥事件,,,则
B. 若,是对立事件,则
C. 若,是独立事件,,,则
D. 若,,且,则,是独立事件
10.某市年经过招商引资后,经济收入较前一年增加了一倍,实现翻番,为更好地了解该市的经济收入的变化情况,统计了该市招商引资前后的年经济收入构成比例,得到如下扇形图:
则下列结论中正确的是( )
A. 招商引资后,工资性收入较前一年增加
B. 招商引资后,转移净收入是前一年的倍
C. 招商引资后,转移净收入与财产净收入的总和超过了该年经济收入的
D. 招商引资后,经营净收入较前一年增加了一倍
11.如图,是边长为的正方形,点,分别为边,的中点,将,,分别沿,,折起,使,,三点重合于点,则( )
A.
B. 点在平面内的射影为的垂心
C. 二面角的余弦值为
D. 若四面体的四个顶点在同一个球面上,则该球的表面积是
三、填空题:本题共3小题,每小题5分,共15分。
12.已知,,,,若点、、在同一条直线上,且,则 ______.
13.用,,表示空间中三条不同的直线,,,表示平面,给出下列命题:
若,,则;
若,,则;
若,,则;
若,,则.
其中真命题的序号是______.
14.在中,设角,,的对边分别是,,,已知,且的面积为,则的周长为______.
四、解答题:本题共4小题,共62分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
如图,四棱锥中,底面为直角梯形,,平面,,,是的中点.
求证:平面平面;
若,求四棱锥的体积.
16.本小题分
在中,内角所对的边分别是,已知.
Ⅰ求证:为等腰三角形;
Ⅱ若是钝角三角形,且面积为,求的值.
17.本小题分
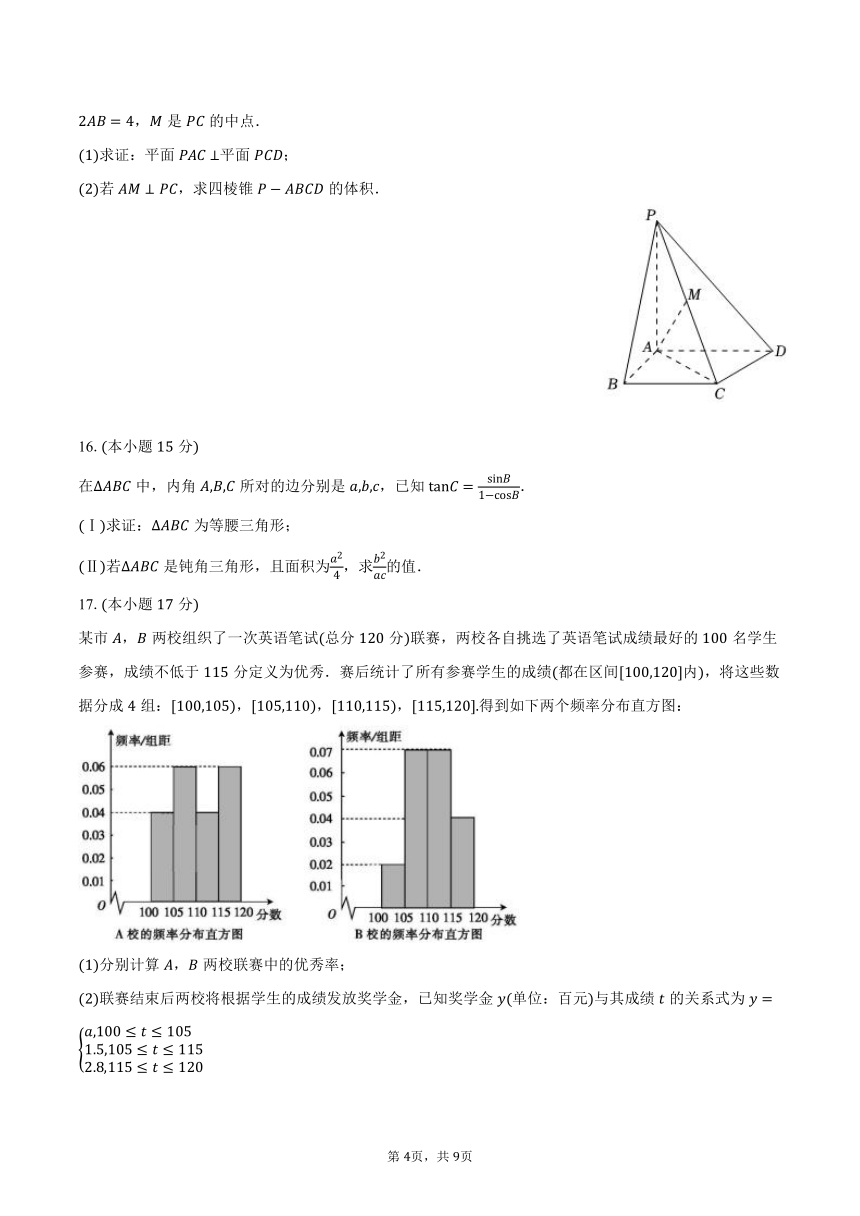
某市,两校组织了一次英语笔试总分分联赛,两校各自挑选了英语笔试成绩最好的名学生参赛,成绩不低于分定义为优秀.赛后统计了所有参赛学生的成绩都在区间内,将这些数据分成组:,,,得到如下两个频率分布直方图:
分别计算,两校联赛中的优秀率;
联赛结束后两校将根据学生的成绩发放奖学金,已知奖学金单位:百元与其成绩的关系式为
当时,试问,两校哪所学校的获奖人数更多?
当时,若以奖学金的总额为判断依据,试问本次联赛,两校哪所学校实力更强?
18.本小题分
“风筝”是中国传统文化中不可或缺的一部分,距今已有多年的历史相传在东周春秋时期,墨翟以木头制成木鸟,是人类最早的风筝起源后来鲁班用竹子,改进墨翟的风筝材质,直至东汉期间,蔡伦改进造纸术后,坊间才开始以纸做风筝,称为“纸鸢”到南北朝时,风筝开始成为传递信息的工具;从隋唐开始,由于造纸业的发达,民间开始用纸来裱糊风筝;到了宋代的时候,放风筝成为人们喜爱的户外活动风筝主要由骨架、风筝面、尾翼、提线、放飞线五部分组成如图就是一个由菱形的风筝面和两个直角三角形尾翼和所组成的风筝其中,,,,现将此风筝的两个尾翼分别沿、折起,使得点与点重合于点,并连结,得到如图所示的四棱锥.
求证:平面;
若为棱上一点,记;
若,求直线与平面所成角的正切值;
是否存在点使得直线与直线所成角为,若存在,请求出的值,若不存在,请说明理由.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.证明:,,,
,
,
,,
又平面,,
又,平面,
又平面,
平面平面;
解:为的中点,,
,
所以四棱锥的体积.
16.解:Ⅰ因为,所以.
由,可得,
所以,变形得,
所以.
在中,,所以,
由正弦定理得,从而为等腰三角形.
Ⅱ由题意得,得.
因为是钝角三角形且,
因此为钝角,,,
所以
,
则.
17.解:由频率分布直方图知,校的优秀率为,
校的优秀率为.
校的获奖人数为,
校的获奖人数为,
所以校的获奖人数更多.
校学生获得的奖学金的总额为:
百元元,
校学生获得的奖学金的总额为:
百元元,
,校实力更强.
18.证明:连接,交于点,
底面为菱形,,
由题意知,,,
,平面,平面,
平面,
又平面,,
,平面,平面,
平面.
解:连结,交于点,
由得平面,
为直线与平面所成角,
,,,
,即为等边三角形,
,,
在中,,,
由余弦定理得,,即,
,
,
,
,
故直线与平面所成角的正切值为.
连结,
,
或其补角为直线与直线所成角,
假设存在点,满足,
由得,,,
在中,,,
由余弦定理得,,
过点作于,
由平面,平面,得,,
由得,,
,,,
在中,由余弦定理得,,
由,平面得,平面,
又平面,,
在中,由勾股定理得,,
在中,,,
由余弦定理得,,
解得或舍负,
故存在使得直线与直线所成角为.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在复平面内,复数对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.已知向量,,,若,则( )
A. B. C. D.
3.从分别写有,,,,,的张卡片中无放回地随机抽取张,则抽到的张卡片上的数字之和是的倍数的概率为( )
A. B. C. D.
4.已知一组数据为,,,,,,,,其平均数、第百分位数和众数的大小关系是( )
A. 平均数第百分位数众数 B. 平均数第百分位数众数
C. 第百分位数众数平均数 D. 平均数第百分位数众数
5.盒内有个红球,个白球,个黑球,从中任取个球,则下列选项中的两个事件互斥而不对立的是( )
A. 至少有个白球;至多有个白球 B. 至少有个白球;至少有个黑球
C. 至少有个白球;红,黑球各个 D. 至少有个白球;没有白球
6.年小明的月工资为元,各种途占比如图所示,年小明的月工资的各种用途占比如图所示,已知年小明每月的旅行费用比年增加了元,则年小明的月工资为( )
A. B. C. D.
7.天气预报说,在今后的三天中,每一天下雨的概率均为,用数字,,,表示下雨,数字,,,,,表示不下雨,由计算机产生如下组随机数:
,,,,,,,,,,
,,,,,,,,,.
由此估计今后三天中至少有一天下雨的概率为( )
A. B. C. D.
8.如图,在单位正方体中,点在线段上运动,给出以下四个命题:
异面直线与间的距离为定值;
三棱锥的体积为定值;
异面直线与直线所成的角为定值;
二面角的大小为定值.
其中真命题有( )
A. 个 B. 个 C. 个 D. 个
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.设,为两个随机事件,以下命题正确的为( )
A. 若,是互斥事件,,,则
B. 若,是对立事件,则
C. 若,是独立事件,,,则
D. 若,,且,则,是独立事件
10.某市年经过招商引资后,经济收入较前一年增加了一倍,实现翻番,为更好地了解该市的经济收入的变化情况,统计了该市招商引资前后的年经济收入构成比例,得到如下扇形图:
则下列结论中正确的是( )
A. 招商引资后,工资性收入较前一年增加
B. 招商引资后,转移净收入是前一年的倍
C. 招商引资后,转移净收入与财产净收入的总和超过了该年经济收入的
D. 招商引资后,经营净收入较前一年增加了一倍
11.如图,是边长为的正方形,点,分别为边,的中点,将,,分别沿,,折起,使,,三点重合于点,则( )
A.
B. 点在平面内的射影为的垂心
C. 二面角的余弦值为
D. 若四面体的四个顶点在同一个球面上,则该球的表面积是
三、填空题:本题共3小题,每小题5分,共15分。
12.已知,,,,若点、、在同一条直线上,且,则 ______.
13.用,,表示空间中三条不同的直线,,,表示平面,给出下列命题:
若,,则;
若,,则;
若,,则;
若,,则.
其中真命题的序号是______.
14.在中,设角,,的对边分别是,,,已知,且的面积为,则的周长为______.
四、解答题:本题共4小题,共62分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
如图,四棱锥中,底面为直角梯形,,平面,,,是的中点.
求证:平面平面;
若,求四棱锥的体积.
16.本小题分
在中,内角所对的边分别是,已知.
Ⅰ求证:为等腰三角形;
Ⅱ若是钝角三角形,且面积为,求的值.
17.本小题分
某市,两校组织了一次英语笔试总分分联赛,两校各自挑选了英语笔试成绩最好的名学生参赛,成绩不低于分定义为优秀.赛后统计了所有参赛学生的成绩都在区间内,将这些数据分成组:,,,得到如下两个频率分布直方图:
分别计算,两校联赛中的优秀率;
联赛结束后两校将根据学生的成绩发放奖学金,已知奖学金单位:百元与其成绩的关系式为
当时,试问,两校哪所学校的获奖人数更多?
当时,若以奖学金的总额为判断依据,试问本次联赛,两校哪所学校实力更强?
18.本小题分
“风筝”是中国传统文化中不可或缺的一部分,距今已有多年的历史相传在东周春秋时期,墨翟以木头制成木鸟,是人类最早的风筝起源后来鲁班用竹子,改进墨翟的风筝材质,直至东汉期间,蔡伦改进造纸术后,坊间才开始以纸做风筝,称为“纸鸢”到南北朝时,风筝开始成为传递信息的工具;从隋唐开始,由于造纸业的发达,民间开始用纸来裱糊风筝;到了宋代的时候,放风筝成为人们喜爱的户外活动风筝主要由骨架、风筝面、尾翼、提线、放飞线五部分组成如图就是一个由菱形的风筝面和两个直角三角形尾翼和所组成的风筝其中,,,,现将此风筝的两个尾翼分别沿、折起,使得点与点重合于点,并连结,得到如图所示的四棱锥.
求证:平面;
若为棱上一点,记;
若,求直线与平面所成角的正切值;
是否存在点使得直线与直线所成角为,若存在,请求出的值,若不存在,请说明理由.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.证明:,,,
,
,
,,
又平面,,
又,平面,
又平面,
平面平面;
解:为的中点,,
,
所以四棱锥的体积.
16.解:Ⅰ因为,所以.
由,可得,
所以,变形得,
所以.
在中,,所以,
由正弦定理得,从而为等腰三角形.
Ⅱ由题意得,得.
因为是钝角三角形且,
因此为钝角,,,
所以
,
则.
17.解:由频率分布直方图知,校的优秀率为,
校的优秀率为.
校的获奖人数为,
校的获奖人数为,
所以校的获奖人数更多.
校学生获得的奖学金的总额为:
百元元,
校学生获得的奖学金的总额为:
百元元,
,校实力更强.
18.证明:连接,交于点,
底面为菱形,,
由题意知,,,
,平面,平面,
平面,
又平面,,
,平面,平面,
平面.
解:连结,交于点,
由得平面,
为直线与平面所成角,
,,,
,即为等边三角形,
,,
在中,,,
由余弦定理得,,即,
,
,
,
,
故直线与平面所成角的正切值为.
连结,
,
或其补角为直线与直线所成角,
假设存在点,满足,
由得,,,
在中,,,
由余弦定理得,,
过点作于,
由平面,平面,得,,
由得,,
,,,
在中,由余弦定理得,,
由,平面得,平面,
又平面,,
在中,由勾股定理得,,
在中,,,
由余弦定理得,,
解得或舍负,
故存在使得直线与直线所成角为.
第1页,共1页
同课章节目录
