苏科版八年级数学下册 9.1 图形的旋转 同步练习(含详解)
文档属性
| 名称 | 苏科版八年级数学下册 9.1 图形的旋转 同步练习(含详解) |
|
|
| 格式 | docx | ||
| 文件大小 | 596.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-02 15:36:28 | ||
图片预览




文档简介
9.1 图形的旋转
一、单选题
1.如图,将正方形ABCD中的阴影三角形绕点A顺时针旋转90°后,得到的图形为( )
A. B.C. D.
2.如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一直线上,则三角板ABC旋转的度数是( )
A.60° B.90° C.120° D.150°
3.如图,将先向上平移1个单位,再绕点按逆时针方向旋转,得到,则点的对应点的坐标是( )
A.(0,4) B.(2,-2) C.(3,-2) D.(-1,4)
4.把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )
A.内部 B.外部 C.边上 D.以上都有可能
5.将绕点旋转得到,则下列作图正确的是( )
A. B. C. D.
6.以原点为中心,将点P(4,5)按逆时针方向旋转90°,得到的点Q所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.下列运动形式属于旋转的是( )
A.在空中上升的氢气球 B.飞驰的火车
C.时钟上钟摆的摆动 D.运动员掷出的标枪
8.如图,将△ABC绕点C(0,1)旋转180°得到△A'B'C,设点A的坐标为,则点的坐标为( )
A. B. C. D.
9.如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC 经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种 变换可以是 ( )
A.△ABC绕点C顺时针旋转90°,再向下平移3
B.△ABC绕点C顺时针旋转90°,再向下平移1
C.△ABC绕点C逆时针旋转90°,再向下平移1
D.△ABC绕点C逆时针旋转90°,再向下平移3
10.如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )
A.1 B.2 C.3 D.不能确定
二、填空题
11.如图,在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为____.
12.如图,在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是__________.
13.如图,将△ABC绕点A逆时针旋转的到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,则BD=_________.
14.如图,点A的坐标为(4,2).将点A绕坐标原点O旋转90°后,再向左平移1个单位长度得到点A′,则过点A′的正比例函数的解析式为_____.
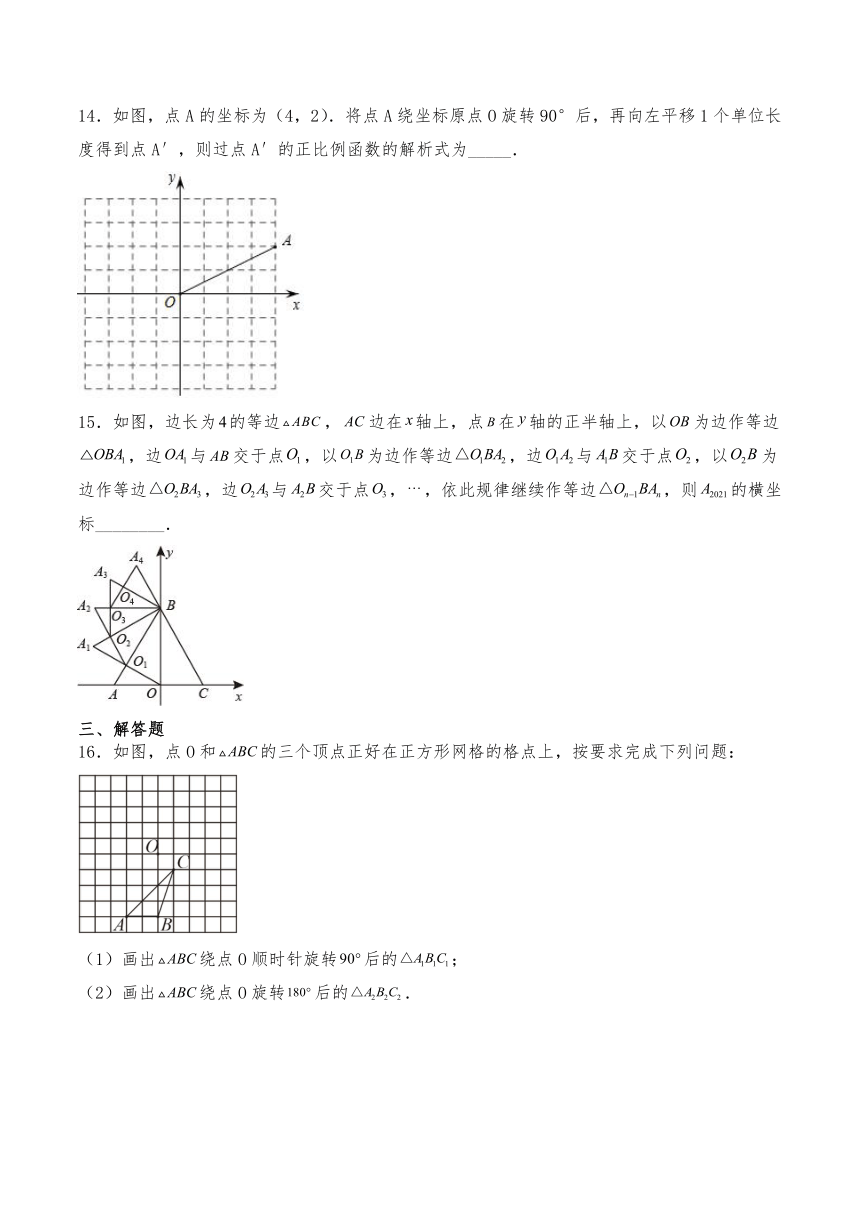
15.如图,边长为的等边,边在轴上,点在轴的正半轴上,以为边作等边,边与交于点,以为边作等边,边与交于点,以为边作等边,边与交于点,,依此规律继续作等边,则的横坐标________.
三、解答题
16.如图,点O和的三个顶点正好在正方形网格的格点上,按要求完成下列问题:
(1)画出绕点O顺时针旋转后的;
(2)画出绕点O旋转后的.
17.如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB'C′的位置,使得CC′AB,求∠CC'A的度数.
答案
一、单选题
1.A
【详解】
试题分析:顺时针90°后,AD转到AB边上,所以,选A.
2.D
【详解】
试题分析:根据旋转角的定义,两对应边的夹角就是旋转角,即可求解.旋转角是∠CAC′=180°﹣30°=150°.
故选D.
3.D
【分析】
根据平移的规律找到A点平移后对应点,然后根据旋转的规律找到旋转后对应点,即可得出的坐标.
【详解】
解:如图所示:A的坐标为(4,2),向上平移1个单位后为(4,3),再绕点P逆时针旋转90°后对应点的坐标为(-1,4).
故选:D.
4.C
【分析】
先根据勾股定理求出两直角三角形的各边长,再由旋转的性质得:∠EBE′=45°,∠E′=∠DEB=90°,求出E′D′与直线AB的交点到B的距离也是5,与AB的值相等,从而可以得出点A在△D′E′B的边上.
【详解】
∵AC=BD=10, 又∵∠ABC=∠DEB=90°,∠A=45°,∠D=30°,
∴BE=5,AB=BC=5,
由三角板DEB绕点B逆时针旋转45°得到△D′E′B,设△D′E′B与直线AB交于G,
可知:∠EBE′=45°,∠E′=∠DEB=90°,
∴△GE′B是等腰直角三角形,且BE′=BE=5,
∴BG=5,
∴BG=AB,
∴点A在△D′E′B的边上,
故选C.
5.D
【分析】
把一个图形绕某一点O转动一个角度的图形变换叫做旋转.
【详解】
解:观察选项中的图形,只有D选项为△ABO绕O点旋转了180°.
6.B
【分析】
根据旋转的性质,以原点为中心,将点P(4,5)按逆时针方向旋转90°,即可得到点Q所在的象限.
【详解】
解:如图,∵点P(4,5)按逆时针方向旋转90°,
得点Q所在的象限为第二象限.
故选:B.
7.C
【分析】
根据旋转的定义逐一进行判断即可得到正确的结论.
【详解】
在空气中上升的氢气球,飞驰的火车,运动员掷出标枪属于平移现象,时钟上钟摆的摆动属于旋转现象.
故答案选:C.
8.D
【详解】
试题分析:根据题意,点A、A′关于点C对称,设点A的坐标是(x,y),则,解得,∴点A的坐标是.故选D.
9.A
【详解】
试题解析:根据图形可以看出,△ABC绕点C顺时针旋转90°,再向下平移3个单位可以得到△ODE.
故选A.
10.A
【分析】如图作辅助线,利用旋转和三角形全等证明△DCG与△DEF全等,再根据全等三角形对应边相等可得EF的长,即△ADE的高,然后得出三角形的面积.
【详解】如图所示,作EF⊥AD交AD延长线于F,作DG⊥BC,
∵CD以D为中心逆时针旋转90°至ED,
∴∠EDF+∠CDF=90°,DE=CD,
又∵∠CDF+∠CDG=90°,
∴∠CDG=∠EDF,
在△DCG与△DEF中,,
∴△DCG≌△DEF(AAS),
∴EF=CG,
∵AD=2,BC=3,
∴CG=BC﹣AD=3﹣2=1,
∴EF=1,
∴△ADE的面积是:×AD×EF=×2×1=1,
故选A.
二、填空题
11.17°
【详解】
解:∵∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,
∴∠B′AC′=33°,∠BAB′=50°,
∴∠B′AC的度数=50° 33°=17°.
故答案为17°.
12.(﹣4,3).
【详解】
试题分析:
解:如图,过点A作AB⊥x轴于B,过点A′作A′B′⊥x轴于B′,
∵OA绕坐标原点O逆时针旋转90°至OA′,
∴OA=OA′,∠AOA′=90°,
∵∠A′OB′+∠AOB=90°,∠AOB+∠OAB=90°,
∴∠OAB=∠A′OB′,
在△AOB和△OA′B′中,
,
∴△AOB≌△OA′B′(AAS),
∴OB′=AB=4,A′B′=OB=3,
∴点A′的坐标为(﹣4,3).
故答案为(﹣4,3).
13..
【详解】
∵将△ABC绕点A逆时针旋转的到△ADE,点C和点E是对应点,
∴AB=AD=1,∠BAD=∠CAE=90°,
∴BD===.
故答案为:.
14.y=﹣x或y=-4x
【详解】
分析:直接利用旋转的性质结合平移的性质得出对应点位置,再利用待定系数法求出正比例函数解析式.
详解:当点A绕坐标原点O逆时针旋转90°后,再向左平移1个单位长度得到点A′,
则A′(-3,4),
设过点A′的正比例函数的解析式为:y=kx,
则4=-3k,
解得:k=-,
则过点A′的正比例函数的解析式为:y=-x,
同理可得:点A绕坐标原点O顺时针旋转90°后,再向左平移1个单位长度得到点A′,此时A′(1,-4),
设过点A′的正比例函数的解析式为:y=k′x,
则-4=k′,
则过点A′的正比例函数的解析式为:y=-4x.
故答案为y=﹣x或y=-4x.
15.0
【分析】
根据正三角形与旋转的特点得到旋转次为一个循环,故可求出的横坐标.
【详解】
解:∵△ABC是正三角形,BO⊥AC
∴∠ABO=30°
同理=30°,
360°÷30°=12,
∴的横坐标旋转次为一个循环,
∵,
∴与在同一直线上,即轴上,
∴的横坐标为.
故答案为:0.
三、解答题
16.(1)
把各点连接至点O,再把每根连线顺时针旋转90°即可得到旋转后的各个点,再连接这些点即可得到旋转后的
(2)
把各点连接至点O,再把每根连线顺时针旋转180°即可得到旋转后的各个点,再连接这些点即可得到旋转后的,由于顺时针旋转180°和逆时针旋转180°效果相同,故该题只存在一种可能:
17.
∵,
∴∠ACC′=∠CAB=70°,
∵△ABC绕点A旋转到△AB′C′的位置,
∴AC=AC′,∠BAB′=∠CAC′,
在△ACC′中,∵AC=AC′
∴∠ACC′=∠CC'A =70°,
一、单选题
1.如图,将正方形ABCD中的阴影三角形绕点A顺时针旋转90°后,得到的图形为( )
A. B.C. D.
2.如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一直线上,则三角板ABC旋转的度数是( )
A.60° B.90° C.120° D.150°
3.如图,将先向上平移1个单位,再绕点按逆时针方向旋转,得到,则点的对应点的坐标是( )
A.(0,4) B.(2,-2) C.(3,-2) D.(-1,4)
4.把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )
A.内部 B.外部 C.边上 D.以上都有可能
5.将绕点旋转得到,则下列作图正确的是( )
A. B. C. D.
6.以原点为中心,将点P(4,5)按逆时针方向旋转90°,得到的点Q所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.下列运动形式属于旋转的是( )
A.在空中上升的氢气球 B.飞驰的火车
C.时钟上钟摆的摆动 D.运动员掷出的标枪
8.如图,将△ABC绕点C(0,1)旋转180°得到△A'B'C,设点A的坐标为,则点的坐标为( )
A. B. C. D.
9.如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC 经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种 变换可以是 ( )
A.△ABC绕点C顺时针旋转90°,再向下平移3
B.△ABC绕点C顺时针旋转90°,再向下平移1
C.△ABC绕点C逆时针旋转90°,再向下平移1
D.△ABC绕点C逆时针旋转90°,再向下平移3
10.如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )
A.1 B.2 C.3 D.不能确定
二、填空题
11.如图,在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为____.
12.如图,在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是__________.
13.如图,将△ABC绕点A逆时针旋转的到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,则BD=_________.
14.如图,点A的坐标为(4,2).将点A绕坐标原点O旋转90°后,再向左平移1个单位长度得到点A′,则过点A′的正比例函数的解析式为_____.
15.如图,边长为的等边,边在轴上,点在轴的正半轴上,以为边作等边,边与交于点,以为边作等边,边与交于点,以为边作等边,边与交于点,,依此规律继续作等边,则的横坐标________.
三、解答题
16.如图,点O和的三个顶点正好在正方形网格的格点上,按要求完成下列问题:
(1)画出绕点O顺时针旋转后的;
(2)画出绕点O旋转后的.
17.如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB'C′的位置,使得CC′AB,求∠CC'A的度数.
答案
一、单选题
1.A
【详解】
试题分析:顺时针90°后,AD转到AB边上,所以,选A.
2.D
【详解】
试题分析:根据旋转角的定义,两对应边的夹角就是旋转角,即可求解.旋转角是∠CAC′=180°﹣30°=150°.
故选D.
3.D
【分析】
根据平移的规律找到A点平移后对应点,然后根据旋转的规律找到旋转后对应点,即可得出的坐标.
【详解】
解:如图所示:A的坐标为(4,2),向上平移1个单位后为(4,3),再绕点P逆时针旋转90°后对应点的坐标为(-1,4).
故选:D.
4.C
【分析】
先根据勾股定理求出两直角三角形的各边长,再由旋转的性质得:∠EBE′=45°,∠E′=∠DEB=90°,求出E′D′与直线AB的交点到B的距离也是5,与AB的值相等,从而可以得出点A在△D′E′B的边上.
【详解】
∵AC=BD=10, 又∵∠ABC=∠DEB=90°,∠A=45°,∠D=30°,
∴BE=5,AB=BC=5,
由三角板DEB绕点B逆时针旋转45°得到△D′E′B,设△D′E′B与直线AB交于G,
可知:∠EBE′=45°,∠E′=∠DEB=90°,
∴△GE′B是等腰直角三角形,且BE′=BE=5,
∴BG=5,
∴BG=AB,
∴点A在△D′E′B的边上,
故选C.
5.D
【分析】
把一个图形绕某一点O转动一个角度的图形变换叫做旋转.
【详解】
解:观察选项中的图形,只有D选项为△ABO绕O点旋转了180°.
6.B
【分析】
根据旋转的性质,以原点为中心,将点P(4,5)按逆时针方向旋转90°,即可得到点Q所在的象限.
【详解】
解:如图,∵点P(4,5)按逆时针方向旋转90°,
得点Q所在的象限为第二象限.
故选:B.
7.C
【分析】
根据旋转的定义逐一进行判断即可得到正确的结论.
【详解】
在空气中上升的氢气球,飞驰的火车,运动员掷出标枪属于平移现象,时钟上钟摆的摆动属于旋转现象.
故答案选:C.
8.D
【详解】
试题分析:根据题意,点A、A′关于点C对称,设点A的坐标是(x,y),则,解得,∴点A的坐标是.故选D.
9.A
【详解】
试题解析:根据图形可以看出,△ABC绕点C顺时针旋转90°,再向下平移3个单位可以得到△ODE.
故选A.
10.A
【分析】如图作辅助线,利用旋转和三角形全等证明△DCG与△DEF全等,再根据全等三角形对应边相等可得EF的长,即△ADE的高,然后得出三角形的面积.
【详解】如图所示,作EF⊥AD交AD延长线于F,作DG⊥BC,
∵CD以D为中心逆时针旋转90°至ED,
∴∠EDF+∠CDF=90°,DE=CD,
又∵∠CDF+∠CDG=90°,
∴∠CDG=∠EDF,
在△DCG与△DEF中,,
∴△DCG≌△DEF(AAS),
∴EF=CG,
∵AD=2,BC=3,
∴CG=BC﹣AD=3﹣2=1,
∴EF=1,
∴△ADE的面积是:×AD×EF=×2×1=1,
故选A.
二、填空题
11.17°
【详解】
解:∵∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,
∴∠B′AC′=33°,∠BAB′=50°,
∴∠B′AC的度数=50° 33°=17°.
故答案为17°.
12.(﹣4,3).
【详解】
试题分析:
解:如图,过点A作AB⊥x轴于B,过点A′作A′B′⊥x轴于B′,
∵OA绕坐标原点O逆时针旋转90°至OA′,
∴OA=OA′,∠AOA′=90°,
∵∠A′OB′+∠AOB=90°,∠AOB+∠OAB=90°,
∴∠OAB=∠A′OB′,
在△AOB和△OA′B′中,
,
∴△AOB≌△OA′B′(AAS),
∴OB′=AB=4,A′B′=OB=3,
∴点A′的坐标为(﹣4,3).
故答案为(﹣4,3).
13..
【详解】
∵将△ABC绕点A逆时针旋转的到△ADE,点C和点E是对应点,
∴AB=AD=1,∠BAD=∠CAE=90°,
∴BD===.
故答案为:.
14.y=﹣x或y=-4x
【详解】
分析:直接利用旋转的性质结合平移的性质得出对应点位置,再利用待定系数法求出正比例函数解析式.
详解:当点A绕坐标原点O逆时针旋转90°后,再向左平移1个单位长度得到点A′,
则A′(-3,4),
设过点A′的正比例函数的解析式为:y=kx,
则4=-3k,
解得:k=-,
则过点A′的正比例函数的解析式为:y=-x,
同理可得:点A绕坐标原点O顺时针旋转90°后,再向左平移1个单位长度得到点A′,此时A′(1,-4),
设过点A′的正比例函数的解析式为:y=k′x,
则-4=k′,
则过点A′的正比例函数的解析式为:y=-4x.
故答案为y=﹣x或y=-4x.
15.0
【分析】
根据正三角形与旋转的特点得到旋转次为一个循环,故可求出的横坐标.
【详解】
解:∵△ABC是正三角形,BO⊥AC
∴∠ABO=30°
同理=30°,
360°÷30°=12,
∴的横坐标旋转次为一个循环,
∵,
∴与在同一直线上,即轴上,
∴的横坐标为.
故答案为:0.
三、解答题
16.(1)
把各点连接至点O,再把每根连线顺时针旋转90°即可得到旋转后的各个点,再连接这些点即可得到旋转后的
(2)
把各点连接至点O,再把每根连线顺时针旋转180°即可得到旋转后的各个点,再连接这些点即可得到旋转后的,由于顺时针旋转180°和逆时针旋转180°效果相同,故该题只存在一种可能:
17.
∵,
∴∠ACC′=∠CAB=70°,
∵△ABC绕点A旋转到△AB′C′的位置,
∴AC=AC′,∠BAB′=∠CAC′,
在△ACC′中,∵AC=AC′
∴∠ACC′=∠CC'A =70°,
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
