苏科版八年级数学下册 9.4.5 正方形 同步练习(含解析)
文档属性
| 名称 | 苏科版八年级数学下册 9.4.5 正方形 同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 444.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-02 15:48:48 | ||
图片预览




文档简介
9.4.5 正方形
一、单选题
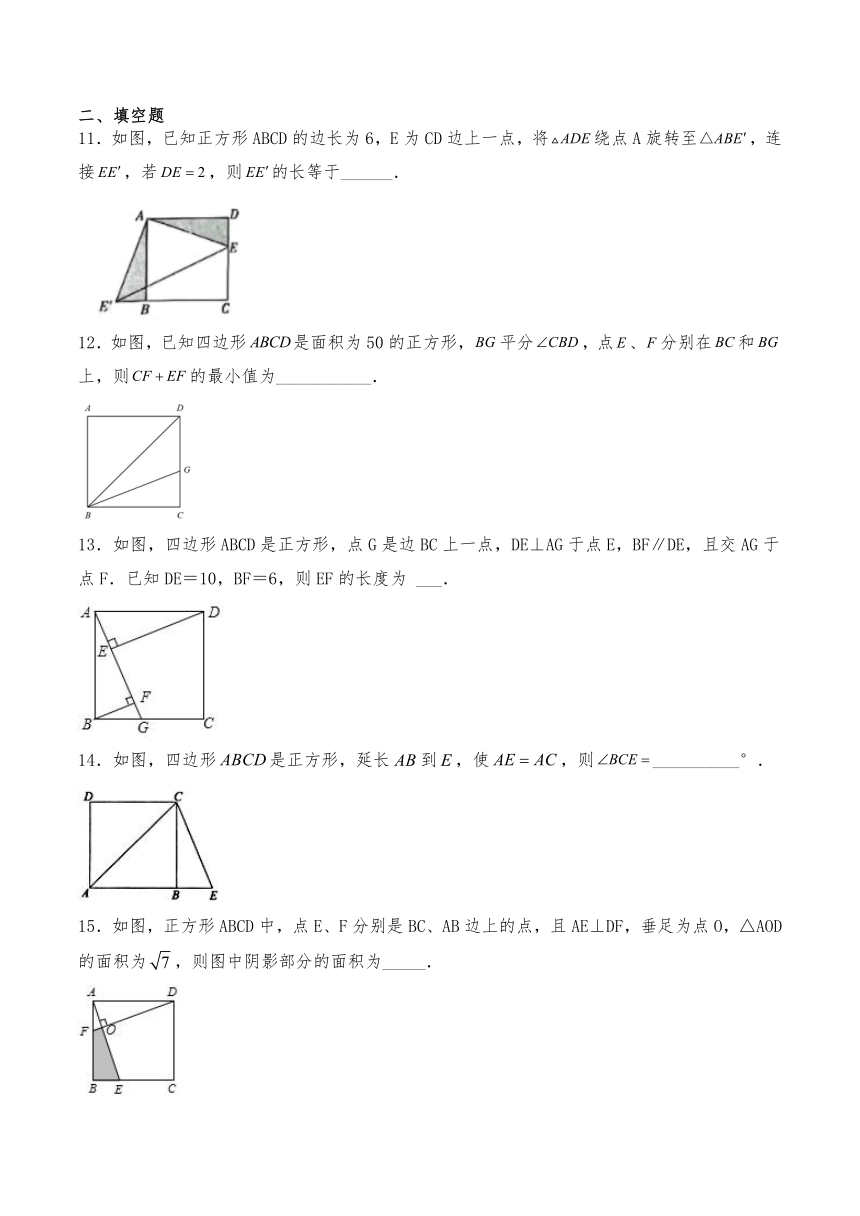
1.如图,直线l上有三个正方形A、B、C,若正方形A、C的边长分别为4和6,则正方形B的面积为( )
A.26 B.49 C.52 D.64
2.正方形具有而矩形不一定有的性质是( )
A.对角线互相垂直 B.对角线相等
C.对角互补 D.四个角相等
3.如图,在正方形ABCD中,,点E在对角线AC上,若,则CDE的面积为( )
A.3 B.4 C.5 D.6
4.如图,正方形ABCD的对角线相交于点O,以点O为顶点的正方形OEGF的两边OE,OF分别交正方形ABCD的两边AB,BC于点M,N,记的面积为,的面积为,若正方形的边长,,则的大小为( )
A.6 B.7 C.8 D.9
5.如图,四边形ABCD是平行四边形,下列结论中错误的是( )
A.当 ABCD是矩形时,∠ABC=90° B.当 ABCD是菱形时,AC⊥BD
C.当 ABCD是正方形时,AC=BD D.当 ABCD是菱形时,AB=AC
6.已知四边形ABCD是平行四边形,下列结论:①当AB=BC时,它是菱形;②当AC⊥BD时,它是菱形;③当∠ABC=90°时,它是矩形;④当AC=BD时,它是正方形,其中错误的有( )
A.1个 B.2个 C.3个 D.4个
7.下列关于 ABCD的叙述,正确的是( )
A.若AB⊥BC,则 ABCD是菱形
B.若AC=BD,则 ABCD是矩形
C.若AC平分∠BAD,则 ABCD是正方形
D.若AC⊥BD,则 ABCD是正方形
8.如图,要使是正方形,需增加条件.在条件①,②,③,④中选取两个作为条件,不正确的是( )
A.①和③ B.②和③ C.①和④ D.③和④
9.对于下列判断:①对角线互相垂直的四边形是矩形;②对角线相等的四边形是矩形;③四边相等的平行四边形是正方形;④对角线互相垂直的矩形是正方形.正确的说法有( )
A.个 B.个 C.个 D.个
10.如图,已知四边形ABCD是平行四边形,下列说法正确的是( )
A.若AB=AD,则 ABCD是矩形
B.若AB=AD,则 ABCD是正方形
C.若AB⊥BC,则 ABCD是矩形
D.若AC⊥BD,则 ABCD是正方形
二、填空题
11.如图,已知正方形ABCD的边长为6,E为CD边上一点,将绕点A旋转至,连接,若,则的长等于______.
12.如图,已知四边形是面积为50的正方形,平分,点、分别在和上,则的最小值为___________.
13.如图,四边形ABCD是正方形,点G是边BC上一点,DE⊥AG于点E,BF∥DE,且交AG于点F.已知DE=10,BF=6,则EF的长度为 ___.
14.如图,四边形是正方形,延长到,使,则__________°.
15.如图,正方形ABCD中,点E、F分别是BC、AB边上的点,且AE⊥DF,垂足为点O,△AOD的面积为,则图中阴影部分的面积为_____.
三、解答题
16.如图所示,在正方形中,点在边上,射线交于点,交的延长线于点.求证:
(1):
(2)若点是上的中点,连接和,求证:.
17.如图,正方形的对角线,交于点,过点作,过点作,与交于点.求证:.
答案
一、单选题
1.C
【分析】
证,推出,,则,,再证,代入求出即可.
【详解】
解:如图,
正方形,的边长分别为4和6,
,,
由正方形的性质得:,,
,,
,
在和中,
,
,
,,
,,
正方形的面积为,
故选:C.
2.A
【分析】
根据正方形的性质,矩形的性质逐一进行判断即可.
【详解】
解:A中对角线互相垂直,是正方形具有而矩形不具有,故符合题意;
B中对角线相等,正方形具有而矩形也具有,故不符合题意;
C中对角互补,正方形具有而矩形也具有,故不符合题意;
D中四个角相等,正方形具有而矩形也具有,故不符合题意;
故选:A.
3.A
【分析】
根据正方形的性质,全等三角形的性质和三角形的面积公式解答即可.
【详解】
∵正方形ABCD,
∴AB=AD,∠BAC=DAC,
∵AE=AE,∴△ABE≌△ADE,
∴=5,同理△CBE≌△CDE,
∴,
∵,
∴CDE的面积为: =3,
故选A.
4.D
【分析】
由题意依据全等三角形的判定得出△BOM≌△CON,进而根据正方形的性质即可得出的大小.
【详解】
解:∵正方形ABCD的对角线AC,BD交于点O,
∴OC=OD=BO=AO,∠ABO=∠ACB=45°,AC⊥BD.
∵∠MOB+∠BON=90°,∠BON+∠CON=90°
∴∠BOM=∠CON,且OC=OB,∠ABO=∠ACB=45°,
∴△BOM≌△CON(ASA),=S△BOM,
∴,
∵=S正方形ABCD,正方形的边长,,
∴=S正方形ABCD -=.
故选:D.
5.D
【分析】
由矩形的四个角是直角可判断A,由菱形的对角线互相垂直可判断B,由正方形的对角线相等可判断C,由菱形的四条边相等可判断D,从而可得答案.
【详解】
解:当 ABCD是矩形时,∠ABC=90°,正确,故A不符合题意;
当 ABCD是菱形时,AC⊥BD,正确,故B不符合题意;
当 ABCD是正方形时,AC=BD,正确,故C不符合题意;
当 ABCD是菱形时,AB=BC,故D符合题意;
故选D
6.A
【分析】
根据矩形、菱形、正方形的判定可以判断题目中的各个小题的结论是否正确,从而可以解答本题.
【详解】
解:四边形是平行四边形,
A、当时,它是菱形,选项不符合题意,
B、当时,它是菱形,选项不符合题意,
C、当时,它是矩形,选项不符合题意,
D、当时,它是矩形,不一定是正方形,选项符合题意,
故选:.
7.B
【分析】
根据菱形的判定方法、矩形的判定方法、正方形的判定方法逐一进行判定即可.
【详解】
解:∵ ABCD中,AB⊥BC,
∴四边形ABCD是矩形,不一定是菱形,选项A不符合题意;
∵ ABCD中,AC=BD,
∴四边形ABCD是矩形,选项B符合题意;
∵ ABCD中,AC平分∠BAD,
∴四边形ABCD是菱形,不一定是正方形,选项C不符合题意;
∵ ABCD中,AC⊥BD,
∴四边形ABCD是菱形,选项D不符合题意;
故选:B.
8.D
【分析】
利用矩形、菱形、正方形之间的关系与区别,结合正方形的判定方法分别判断得出即可.
【详解】
解: A、∵四边形ABCD是平行四边形,
当①时,是菱形,
当③时,菱形ABCD是正方形,故此选项正确,不合题意;
B、∵四边形ABCD是平行四边形,
当②时,是菱形,
当③时,菱形ABCD是正方形,故此选项正确,不合题意;
C、∵四边形ABCD是平行四边形,
∴当①时,是菱形,
当④时,菱形ABCD是正方形,故此选项正确,不合题意.
D、∵四边形ABCD是平行四边形,
∴当④时,是矩形,
当③时,这是矩形的性质,无法得出四边形ABCD是正方形,故此选项错误,符合题意;
故选:D.
9.A
【分析】
根据菱形、矩形、正方形的判定方法分别分析即可求解.
【详解】
解:①对角线互相垂直的四边形不一定是矩形,故①错误;
②对角线相等的四边形不一定是矩形,故②错误;
③四边相等的平行四边形是菱形,故③错误;
④对角线互相垂直的矩形是正方形,故④正确.
故选:A.
10.C
【分析】
根据矩形和正方形的判定定理逐项判断,即可解答.
【详解】
解:A、因为邻边相等的平行四边形是菱形,故A错误,不符合题意;
B、因为邻边相等的平行四边形是菱形,故B错误,不符合题意;
C、若AB⊥BC,则 ABCD是矩形,故C正确,符合题意;
D、对角线互相垂直的平行四边形是菱形,故D错误,不符合题意;
故选:C.
二、填空题
11.4
【分析】
在正方形ABCD中,BE′=DE=2,所以在直角三角形E′CE中,E′C=8,CE=4,利用勾股定理求得EE′的长即可.
【详解】
解:在正方形ABCD中,∠C=90°,
由旋转得,BE′=DE=2,
∴E′C=8,CE=4,
∴在直角三角形E′CE中,
EE′===4.
故答案为4.
12.5
【分析】
连接交于,交于,过作于,则,可得
由角平分线的性质可得到:,继而可得,根据正方形的面积可得,再根据勾股定理计算AC即可求解.
【详解】
解:如图,连接交于,交于,过作于,则,
∵平分,
∴,
∴,
∵四边形是面积为50的正方形,
∴,
∴在中,,
∴,
∴的最小值为5.
13.4
【分析】
因为AF=AE+EF,则可以通过证明△ABF≌△DAE,从而得到AE=BF,AF=DE
便得到了EF=DE - BF.
【详解】
证明:∵ABCD是正方形,
∴AD=AB,∠BAD=90°
∵DE⊥AG,
∴∠AED=90°
∴∠ADE+∠DAE=90°
又∵∠BAF+∠DAE=∠BAD=90°,
∴∠ADE=∠BAF.
∵BF∥DE,
∴∠AFB=∠DEG=∠AED.
在△ABF与△DAE中, ,
∴△ABF≌△DAE(AAS).
∴BF=AE,AF=DE
∵AF=AE+EF,
∴EF=DE - BF=4,
故答案为:4.
14.22.5
【分析】
根据正方形的性质求出∠CAB=∠ACB=45°,再根据AC=AE求出∠ACE=67.5°,由此即可求出答案.
【详解】
∵四边形ABCD是正方形,
∴∠DAB=∠DCB=90°,
∵AC是对角线,
∴∠CAB=∠ACB=45°,
∵AC=AE,
∴∠ACE=67.5°,
∴∠BCE=∠ACE-∠ACB=22.5°,
故答案为:22.5°.
15.
【分析】
先证得△ADF△BAE,再利用等量代换即可求得阴影部分的面积等于△AOD的面积.
【详解】
正方形ABCD中,
∠DAF=∠ABE=90,AD=AB,
∵AE⊥DF,
∴∠DOA=∠DAF =90,
∴∠DAO+∠ADF =∠DAO +∠FAO =90,
∴∠ADF =∠FAO,
在△ADF和△BAE中,
,
∴△ADF△BAE,
∴,
∴,
∴.
故答案为:.
三、解答题
16.
(1)证明:∵四边形ABCD是正方形,
∴AD=CD,∠ADB=∠CDB=45°,
在△ADE和△CDE中,
,
∴△ADE≌△CDE(SAS);
(2)证明:∵△ADE≌△CDE,
∴∠1=∠2,
∵在Rt△FCG中,点H是FG上的中点,
∴CH=FG=GH,
∴∠4=∠G,
∵ADBG,
∴∠1=∠G,
∴∠4=∠1,
∵∠2=∠1,
∴∠4=∠2,
∵∠4+∠3=90°,
∴∠2+∠3=90°,
∴EC⊥CH.
17.
证明:∵,,
∴四边形是平行四边形.
∵四边形是正方形,
∴,,
∴四边形是正方形,
∴.
一、单选题
1.如图,直线l上有三个正方形A、B、C,若正方形A、C的边长分别为4和6,则正方形B的面积为( )
A.26 B.49 C.52 D.64
2.正方形具有而矩形不一定有的性质是( )
A.对角线互相垂直 B.对角线相等
C.对角互补 D.四个角相等
3.如图,在正方形ABCD中,,点E在对角线AC上,若,则CDE的面积为( )
A.3 B.4 C.5 D.6
4.如图,正方形ABCD的对角线相交于点O,以点O为顶点的正方形OEGF的两边OE,OF分别交正方形ABCD的两边AB,BC于点M,N,记的面积为,的面积为,若正方形的边长,,则的大小为( )
A.6 B.7 C.8 D.9
5.如图,四边形ABCD是平行四边形,下列结论中错误的是( )
A.当 ABCD是矩形时,∠ABC=90° B.当 ABCD是菱形时,AC⊥BD
C.当 ABCD是正方形时,AC=BD D.当 ABCD是菱形时,AB=AC
6.已知四边形ABCD是平行四边形,下列结论:①当AB=BC时,它是菱形;②当AC⊥BD时,它是菱形;③当∠ABC=90°时,它是矩形;④当AC=BD时,它是正方形,其中错误的有( )
A.1个 B.2个 C.3个 D.4个
7.下列关于 ABCD的叙述,正确的是( )
A.若AB⊥BC,则 ABCD是菱形
B.若AC=BD,则 ABCD是矩形
C.若AC平分∠BAD,则 ABCD是正方形
D.若AC⊥BD,则 ABCD是正方形
8.如图,要使是正方形,需增加条件.在条件①,②,③,④中选取两个作为条件,不正确的是( )
A.①和③ B.②和③ C.①和④ D.③和④
9.对于下列判断:①对角线互相垂直的四边形是矩形;②对角线相等的四边形是矩形;③四边相等的平行四边形是正方形;④对角线互相垂直的矩形是正方形.正确的说法有( )
A.个 B.个 C.个 D.个
10.如图,已知四边形ABCD是平行四边形,下列说法正确的是( )
A.若AB=AD,则 ABCD是矩形
B.若AB=AD,则 ABCD是正方形
C.若AB⊥BC,则 ABCD是矩形
D.若AC⊥BD,则 ABCD是正方形
二、填空题
11.如图,已知正方形ABCD的边长为6,E为CD边上一点,将绕点A旋转至,连接,若,则的长等于______.
12.如图,已知四边形是面积为50的正方形,平分,点、分别在和上,则的最小值为___________.
13.如图,四边形ABCD是正方形,点G是边BC上一点,DE⊥AG于点E,BF∥DE,且交AG于点F.已知DE=10,BF=6,则EF的长度为 ___.
14.如图,四边形是正方形,延长到,使,则__________°.
15.如图,正方形ABCD中,点E、F分别是BC、AB边上的点,且AE⊥DF,垂足为点O,△AOD的面积为,则图中阴影部分的面积为_____.
三、解答题
16.如图所示,在正方形中,点在边上,射线交于点,交的延长线于点.求证:
(1):
(2)若点是上的中点,连接和,求证:.
17.如图,正方形的对角线,交于点,过点作,过点作,与交于点.求证:.
答案
一、单选题
1.C
【分析】
证,推出,,则,,再证,代入求出即可.
【详解】
解:如图,
正方形,的边长分别为4和6,
,,
由正方形的性质得:,,
,,
,
在和中,
,
,
,,
,,
正方形的面积为,
故选:C.
2.A
【分析】
根据正方形的性质,矩形的性质逐一进行判断即可.
【详解】
解:A中对角线互相垂直,是正方形具有而矩形不具有,故符合题意;
B中对角线相等,正方形具有而矩形也具有,故不符合题意;
C中对角互补,正方形具有而矩形也具有,故不符合题意;
D中四个角相等,正方形具有而矩形也具有,故不符合题意;
故选:A.
3.A
【分析】
根据正方形的性质,全等三角形的性质和三角形的面积公式解答即可.
【详解】
∵正方形ABCD,
∴AB=AD,∠BAC=DAC,
∵AE=AE,∴△ABE≌△ADE,
∴=5,同理△CBE≌△CDE,
∴,
∵,
∴CDE的面积为: =3,
故选A.
4.D
【分析】
由题意依据全等三角形的判定得出△BOM≌△CON,进而根据正方形的性质即可得出的大小.
【详解】
解:∵正方形ABCD的对角线AC,BD交于点O,
∴OC=OD=BO=AO,∠ABO=∠ACB=45°,AC⊥BD.
∵∠MOB+∠BON=90°,∠BON+∠CON=90°
∴∠BOM=∠CON,且OC=OB,∠ABO=∠ACB=45°,
∴△BOM≌△CON(ASA),=S△BOM,
∴,
∵=S正方形ABCD,正方形的边长,,
∴=S正方形ABCD -=.
故选:D.
5.D
【分析】
由矩形的四个角是直角可判断A,由菱形的对角线互相垂直可判断B,由正方形的对角线相等可判断C,由菱形的四条边相等可判断D,从而可得答案.
【详解】
解:当 ABCD是矩形时,∠ABC=90°,正确,故A不符合题意;
当 ABCD是菱形时,AC⊥BD,正确,故B不符合题意;
当 ABCD是正方形时,AC=BD,正确,故C不符合题意;
当 ABCD是菱形时,AB=BC,故D符合题意;
故选D
6.A
【分析】
根据矩形、菱形、正方形的判定可以判断题目中的各个小题的结论是否正确,从而可以解答本题.
【详解】
解:四边形是平行四边形,
A、当时,它是菱形,选项不符合题意,
B、当时,它是菱形,选项不符合题意,
C、当时,它是矩形,选项不符合题意,
D、当时,它是矩形,不一定是正方形,选项符合题意,
故选:.
7.B
【分析】
根据菱形的判定方法、矩形的判定方法、正方形的判定方法逐一进行判定即可.
【详解】
解:∵ ABCD中,AB⊥BC,
∴四边形ABCD是矩形,不一定是菱形,选项A不符合题意;
∵ ABCD中,AC=BD,
∴四边形ABCD是矩形,选项B符合题意;
∵ ABCD中,AC平分∠BAD,
∴四边形ABCD是菱形,不一定是正方形,选项C不符合题意;
∵ ABCD中,AC⊥BD,
∴四边形ABCD是菱形,选项D不符合题意;
故选:B.
8.D
【分析】
利用矩形、菱形、正方形之间的关系与区别,结合正方形的判定方法分别判断得出即可.
【详解】
解: A、∵四边形ABCD是平行四边形,
当①时,是菱形,
当③时,菱形ABCD是正方形,故此选项正确,不合题意;
B、∵四边形ABCD是平行四边形,
当②时,是菱形,
当③时,菱形ABCD是正方形,故此选项正确,不合题意;
C、∵四边形ABCD是平行四边形,
∴当①时,是菱形,
当④时,菱形ABCD是正方形,故此选项正确,不合题意.
D、∵四边形ABCD是平行四边形,
∴当④时,是矩形,
当③时,这是矩形的性质,无法得出四边形ABCD是正方形,故此选项错误,符合题意;
故选:D.
9.A
【分析】
根据菱形、矩形、正方形的判定方法分别分析即可求解.
【详解】
解:①对角线互相垂直的四边形不一定是矩形,故①错误;
②对角线相等的四边形不一定是矩形,故②错误;
③四边相等的平行四边形是菱形,故③错误;
④对角线互相垂直的矩形是正方形,故④正确.
故选:A.
10.C
【分析】
根据矩形和正方形的判定定理逐项判断,即可解答.
【详解】
解:A、因为邻边相等的平行四边形是菱形,故A错误,不符合题意;
B、因为邻边相等的平行四边形是菱形,故B错误,不符合题意;
C、若AB⊥BC,则 ABCD是矩形,故C正确,符合题意;
D、对角线互相垂直的平行四边形是菱形,故D错误,不符合题意;
故选:C.
二、填空题
11.4
【分析】
在正方形ABCD中,BE′=DE=2,所以在直角三角形E′CE中,E′C=8,CE=4,利用勾股定理求得EE′的长即可.
【详解】
解:在正方形ABCD中,∠C=90°,
由旋转得,BE′=DE=2,
∴E′C=8,CE=4,
∴在直角三角形E′CE中,
EE′===4.
故答案为4.
12.5
【分析】
连接交于,交于,过作于,则,可得
由角平分线的性质可得到:,继而可得,根据正方形的面积可得,再根据勾股定理计算AC即可求解.
【详解】
解:如图,连接交于,交于,过作于,则,
∵平分,
∴,
∴,
∵四边形是面积为50的正方形,
∴,
∴在中,,
∴,
∴的最小值为5.
13.4
【分析】
因为AF=AE+EF,则可以通过证明△ABF≌△DAE,从而得到AE=BF,AF=DE
便得到了EF=DE - BF.
【详解】
证明:∵ABCD是正方形,
∴AD=AB,∠BAD=90°
∵DE⊥AG,
∴∠AED=90°
∴∠ADE+∠DAE=90°
又∵∠BAF+∠DAE=∠BAD=90°,
∴∠ADE=∠BAF.
∵BF∥DE,
∴∠AFB=∠DEG=∠AED.
在△ABF与△DAE中, ,
∴△ABF≌△DAE(AAS).
∴BF=AE,AF=DE
∵AF=AE+EF,
∴EF=DE - BF=4,
故答案为:4.
14.22.5
【分析】
根据正方形的性质求出∠CAB=∠ACB=45°,再根据AC=AE求出∠ACE=67.5°,由此即可求出答案.
【详解】
∵四边形ABCD是正方形,
∴∠DAB=∠DCB=90°,
∵AC是对角线,
∴∠CAB=∠ACB=45°,
∵AC=AE,
∴∠ACE=67.5°,
∴∠BCE=∠ACE-∠ACB=22.5°,
故答案为:22.5°.
15.
【分析】
先证得△ADF△BAE,再利用等量代换即可求得阴影部分的面积等于△AOD的面积.
【详解】
正方形ABCD中,
∠DAF=∠ABE=90,AD=AB,
∵AE⊥DF,
∴∠DOA=∠DAF =90,
∴∠DAO+∠ADF =∠DAO +∠FAO =90,
∴∠ADF =∠FAO,
在△ADF和△BAE中,
,
∴△ADF△BAE,
∴,
∴,
∴.
故答案为:.
三、解答题
16.
(1)证明:∵四边形ABCD是正方形,
∴AD=CD,∠ADB=∠CDB=45°,
在△ADE和△CDE中,
,
∴△ADE≌△CDE(SAS);
(2)证明:∵△ADE≌△CDE,
∴∠1=∠2,
∵在Rt△FCG中,点H是FG上的中点,
∴CH=FG=GH,
∴∠4=∠G,
∵ADBG,
∴∠1=∠G,
∴∠4=∠1,
∵∠2=∠1,
∴∠4=∠2,
∵∠4+∠3=90°,
∴∠2+∠3=90°,
∴EC⊥CH.
17.
证明:∵,,
∴四边形是平行四边形.
∵四边形是正方形,
∴,,
∴四边形是正方形,
∴.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
