指数函数及其性质

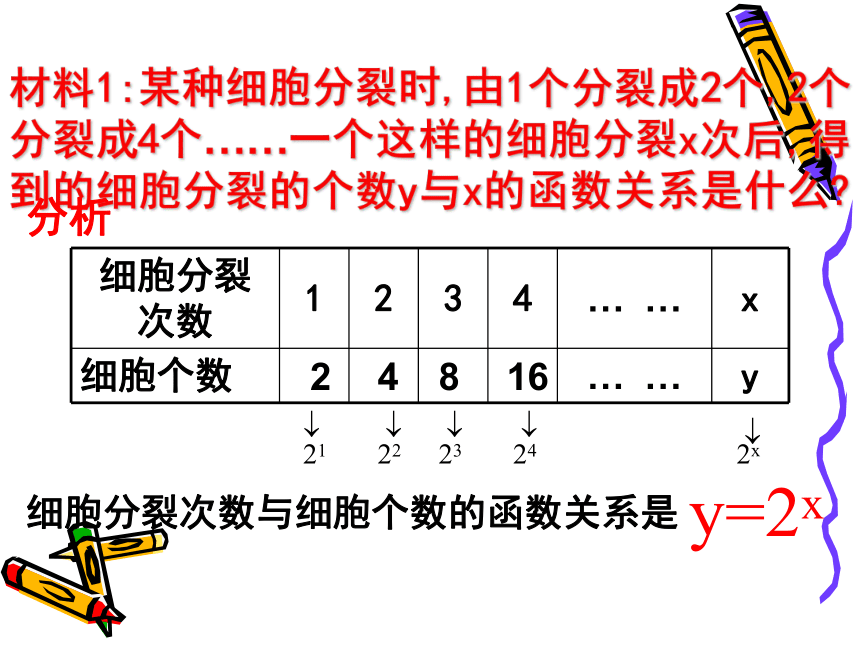
课件35张PPT。材料1:某种细胞分裂时,由1个分裂成2个,2个分裂成4个……一个这样的细胞分裂x次后,得到的细胞分裂的个数y与x的函数关系是什么?分析24816细胞分裂次数与细胞个数的函数关系是
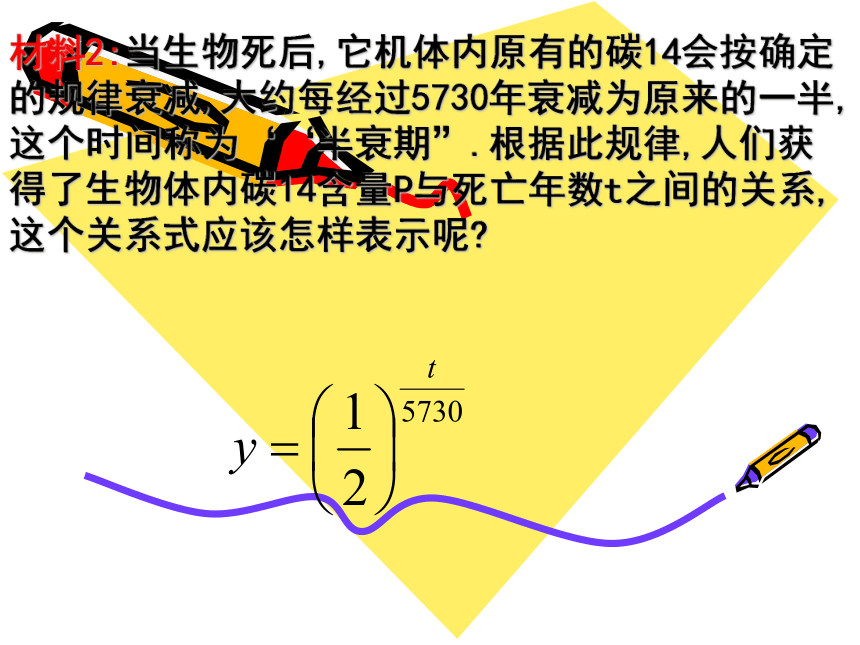
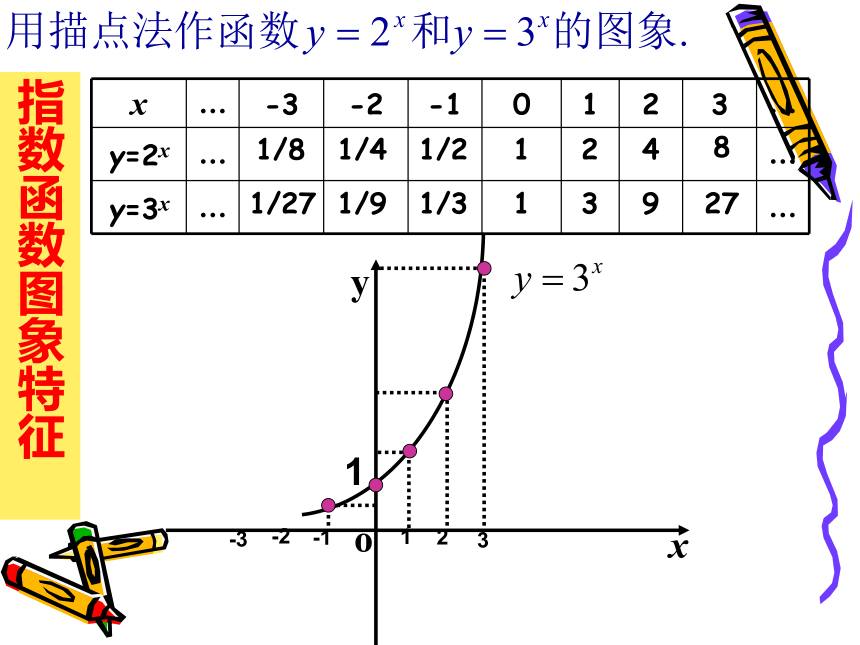
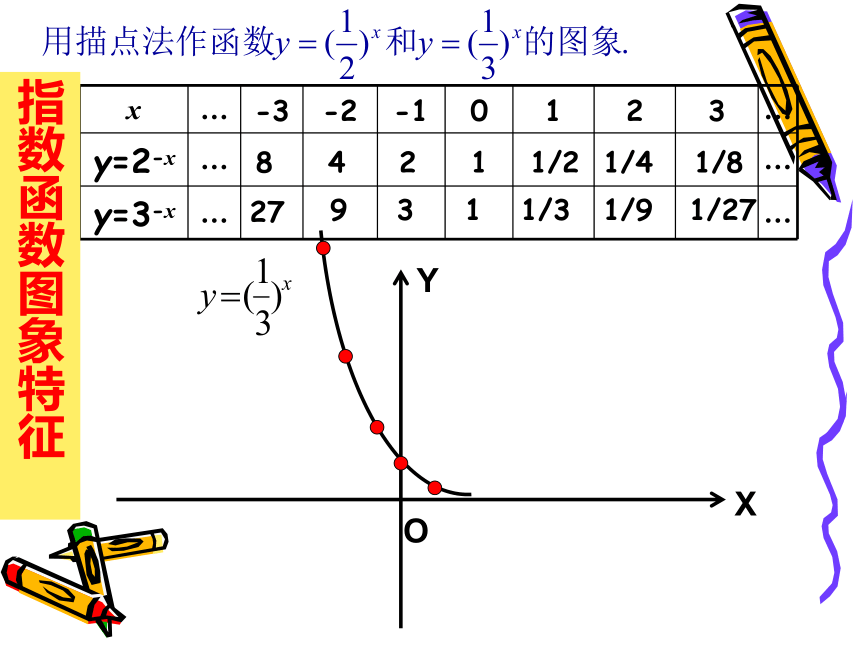
y=2x材料2:当生物死后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为‘‘半衰期”.根据此规律,人们获得了生物体内碳14含量P与死亡年数t之间的关系,这个关系式应该怎样表示呢?思考你能从以上两个解析式中抽象出一个更具有一般性的函数模型吗？y=ax(a>0,a≠1)，这就是我们下面所要研究的一类重要函数模型--- 。指数函数指数函数及其性质一般地，函数叫做指数函数，其中x是自变量，同时规定 a＞0 且 a≠1, 函数的定义域是R.１、指数函数的定义 思考：为何规定a>0，且a≠1 ?巩固练习指数函数图象特征 11/81/41/212481/927191/31/273定义域：值域：单调性：奇偶性：公共点：增函数非奇非偶1/81/41/212481/927191/31/273指数函数图象特征 定义域：值域：单调性：奇偶性：公共点：减函数非奇非偶探究一：函数 的图象和函数 的图象有什么关系？ 猜想：
关于y轴对称？ y=1两函数图象有什么共同点，又有什么不同特征?影响函数图象特征的主要因素是什么？y=ax (a>0,a≠1)叫做指数函数x∈Ry∈R+
非奇非偶a>1,增00,y>1
x<0,00,0x<0,y>14、 图 象 性 质yx0(0,1)y=ax
(a>1)yx(0,1)0y=ax
(01a,b,c,d探究二：结论：　　　例3　如图，曲线是指数函　　　的图
象，已知　取　　　　 四个值，则相应于曲线　　　　　 的　依次为（　）DB基础练习y=2x思考结论:两个函数图象关于y轴对称因为ｙ=2x的图象上的点P(x,y)与
图象上的点P’(-x,y)
关于y轴对称例4 已知指数函数f(x)=ax (a>0,且a≠1）的图象经过点（3，π），求f(0)、f(1)、f(-3)的值.例题与练习练习1、已知y=f（x）是指数函数，且f（2）=4，求函数y=f（x）的解析式。练习2、已知y=(2a-1)x是指数函数，求实数a的取值范围。练习2答：a＞ 且a≠1例5、解下列不等式113232)21()3(;2)2()1()1(622+-++-++-==>=xxxxxxyyaay；区间。、求出下列函数的单调例经过1年 人口约为：经过2年 人口约为：经过3年 人口约为：经过x年 人口约为：解：1、指数函数的定义。
2、指数函数简图的作法以及应注意的地方。
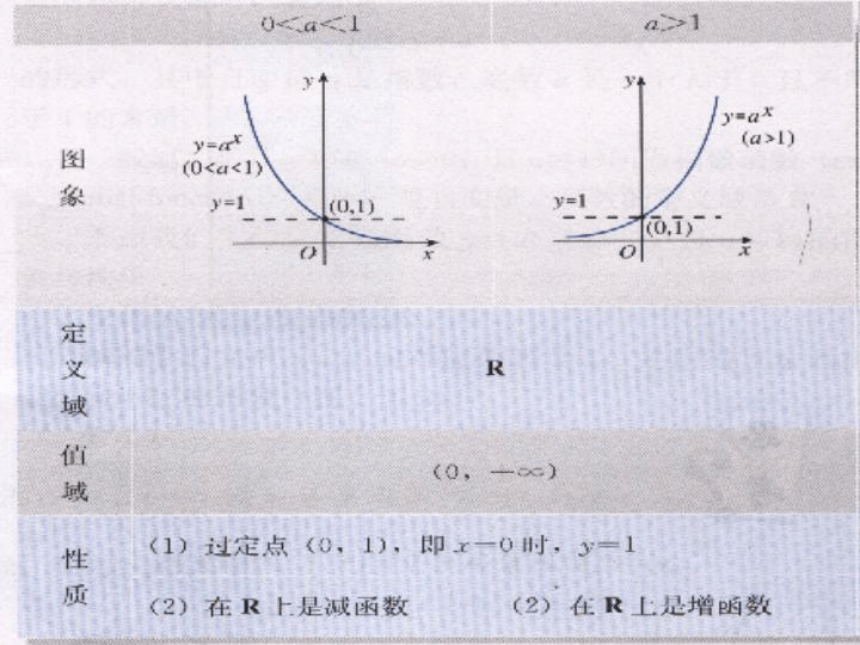
3、指数函数的图像和性质。小结2.指数函数的图象和性质1.图象全在x轴上方，与x轴无限接近。1.定义域为R，值域为(0,+?).2.图象过定点（0，1）2.当x=0时，y=13.自左向右图象逐渐上升3.自左向右图象逐渐下降3.在R上是增函数3.在R上是减函数4.图象分布在左下和右上两个区域内4.图象分布在左上和右下两个区域内4.当x>0时,y>1;当x<0时,00时, 01.5.图象无对称性(既不关于原点对称,也不关于y轴对称)5.既不是奇函数也不是偶函数.y=ax (a>0,a≠1)叫做指数函数x∈Ry∈R+
非奇非偶a>1,增00,y>1
x<0,00,0x<0,y>12、1 y=10xy=2xy=x4.2 指数函数 y = a x ( a < 0, 且 a ≠0 )一般性质：（1）图像沿 x 轴 向左右方向无限延伸，
函数的 定义域为 R 。 （2）图像都在 x 轴上方，函数的值域是R+,（3）图像都经过 点(0 ,1 ), 即 f (0 ) = 1（4）当 a >1 时, 在 (-∞,+ ∞)上是增函数;
0xy（5）当 a >1 时，若 x > 0 , 则 y >1
(a 越大,图像上方越较靠近 y 轴 )若 x < 0 , 则 0当 0 0 , 则 01
(a 越小,图像上方越较靠近 y 轴 )
当 0 当x > 0，0 x<0 ， y>10 < a < 1
指数函数的图象和性质练习：已知函数
（1）求函数f(x)的定义域和值域；
（2）讨论函数f(x)的奇偶性；
（3）讨论函数f(x)的单调性．