2023-2024学年四川省成都市第七中学高二下学期期末考试数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年四川省成都市第七中学高二下学期期末考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 331.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-02 19:51:14 | ||
图片预览



文档简介
2023-2024学年四川省成都市第七中学高二下学期期末考试数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若集合,,则集合的真子集个数为( )
A. B. C. D.
2.已知向量,,若,则( )
A. B. C. D.
3.已知是直线的方向向量,是平面的法向量,若,则( )
A. B. C. D.
4.已知等差数列和的前项和分别为和,且,则( )
A. B. C. D.
5.从,,,中任取个数字,从,中任取个数字,可以组成没有重复数字的三位数的个数是( )
A. B. C. D.
6.某公司对员工的工作绩效进行评估,得到一组数据,后来复查数据时,又将重复记录在数据中,则这组新的数据和原来的数据相比,一定不会改变的是( )
A. 平均数 B. 中位数 C. 极差 D. 众数
7.抛物线绕它的对称轴旋转所得到的曲面叫抛物面,用于加热水和水壶食物的太阳灶应用了抛物线的光学性质:一束平行于抛物线对称轴的光线,经过抛物面的反射后,集中于它的焦点.已知一束平行反射镜于轴的入射光线与抛物线的交点为,则反射光线所在直线被抛物线截得的弦长为( )
A. B. C. D.
8.函数的零点个数是( )
A. B. C. D.
二、多选题:本题共3小题,共15分。在每小题给出的选项中,有多项符合题目要求。
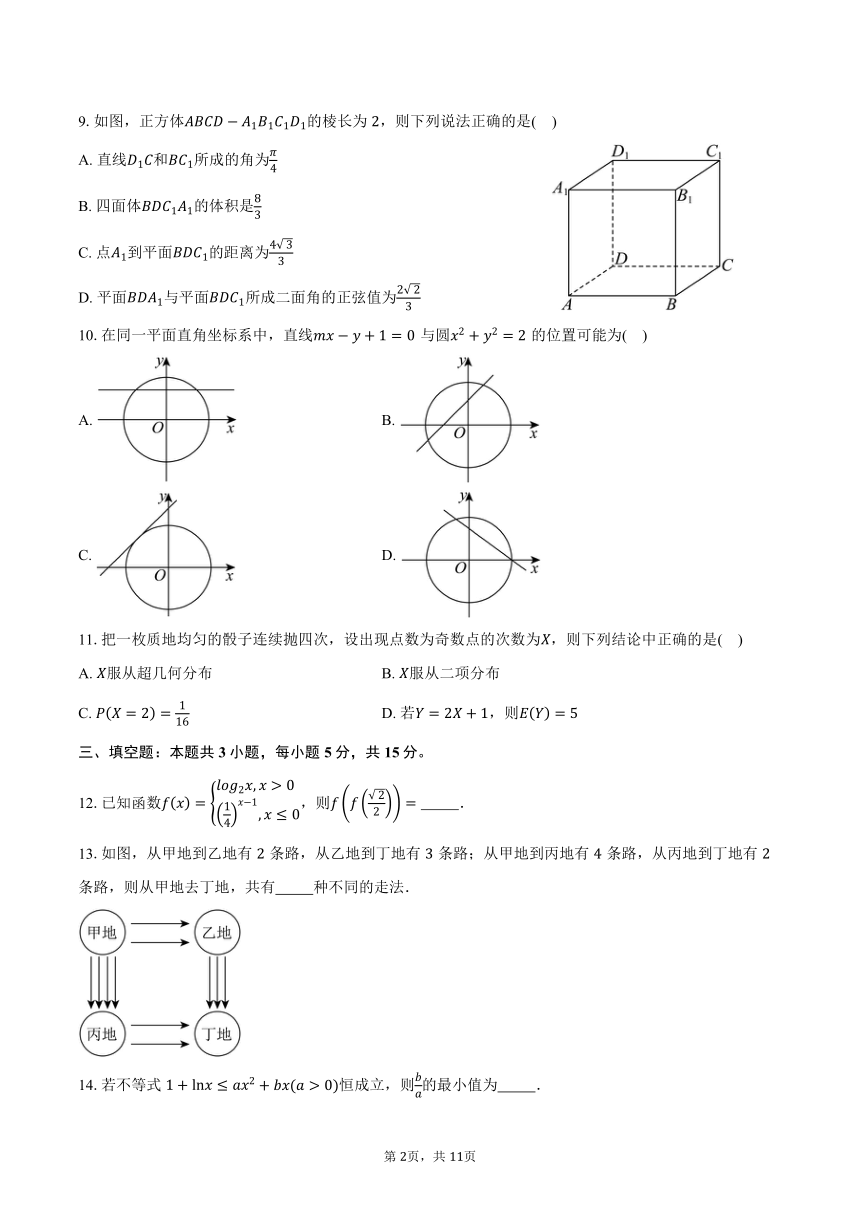
9.如图,正方体的棱长为,则下列说法正确的是( )
A. 直线和所成的角为
B. 四面体的体积是
C. 点到平面的距离为
D. 平面与平面所成二面角的正弦值为
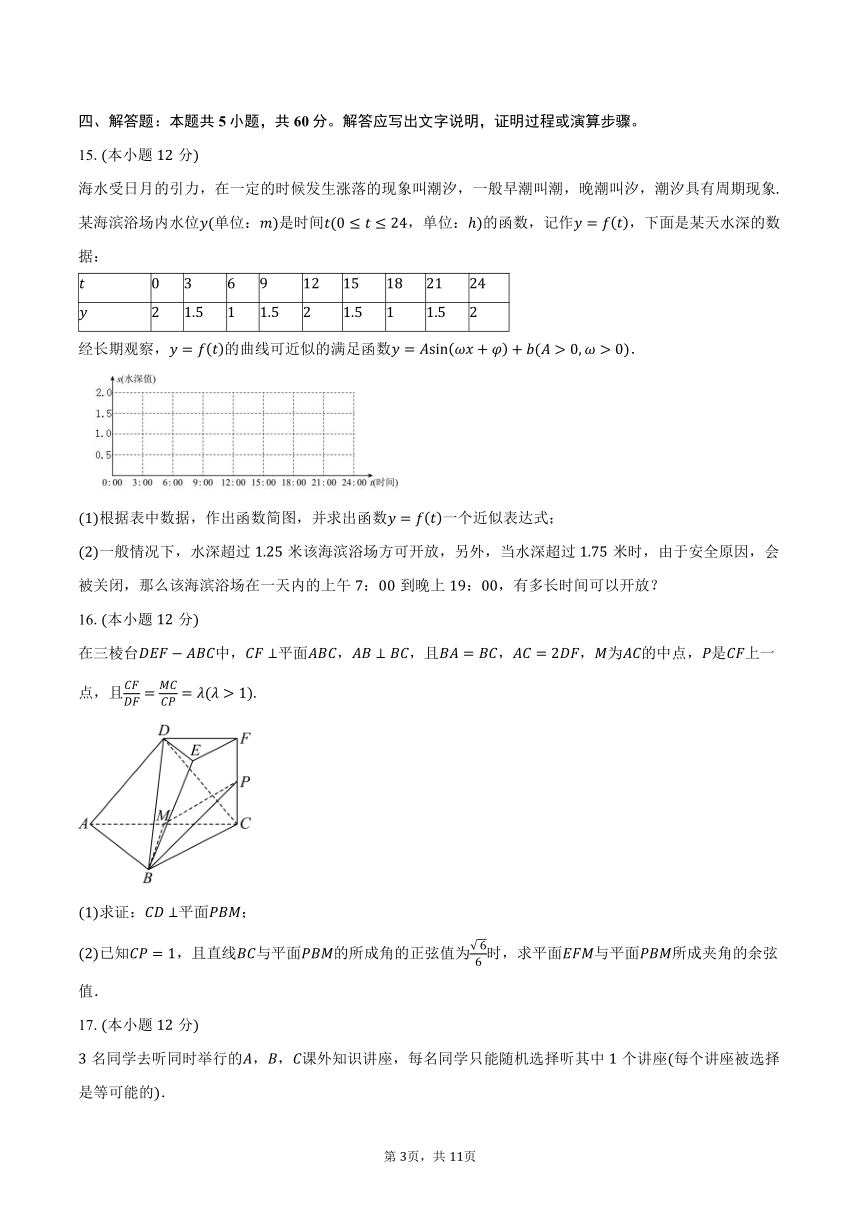
10.在同一平面直角坐标系中,直线与圆的位置可能为( )
A. B.
C. D.
11.把一枚质地均匀的骰子连续抛四次,设出现点数为奇数点的次数为,则下列结论中正确的是( )
A. 服从超几何分布 B. 服从二项分布
C. D. 若,则
三、填空题:本题共3小题,每小题5分,共15分。
12.已知函数,则 .
13.如图,从甲地到乙地有条路,从乙地到丁地有条路;从甲地到丙地有条路,从丙地到丁地有条路,则从甲地去丁地,共有 种不同的走法.
14.若不等式恒成立,则的最小值为 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
海水受日月的引力,在一定的时候发生涨落的现象叫潮汐,一般早潮叫潮,晚潮叫汐,潮汐具有周期现象某海滨浴场内水位单位:是时间,单位:的函数,记作,下面是某天水深的数据:
经长期观察,的曲线可近似的满足函数.
根据表中数据,作出函数简图,并求出函数一个近似表达式;
一般情况下,水深超过米该海滨浴场方可开放,另外,当水深超过米时,由于安全原因,会被关闭,那么该海滨浴场在一天内的上午:到晚上:,有多长时间可以开放?
16.本小题分
在三棱台中,平面,,且,,为的中点,是上一点,且
求证:平面;
已知,且直线与平面的所成角的正弦值为时,求平面与平面所成夹角的余弦值.
17.本小题分
名同学去听同时举行的,,课外知识讲座,每名同学只能随机选择听其中个讲座每个讲座被选择是等可能的.
记选择课外知识讲座的人数为随机变量,求的分布列与数学期望;
对于两个不相互独立的事件,,若,,称为事件,的相关系数.
已知,证明;
记事件“课外知识讲座有同学选择”,事件“至少有两个课外知识讲座有同学选择”,判断事件,是否独立,若独立,说明理由;若不独立,求.
18.本小题分
已知点为坐标原点,将向量绕逆时针旋转角后得到向量.
若,求的坐标;
若,求的坐标用表示;
若点在抛物线上,且为等边三角形,讨论的个数.
19.本小题分
设实系数一元二次方程,有两根,
则方程可变形为,展开得,
比较可以得到
这表明,任何一个一元二次方程的根与系数的关系为:两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比这就是我们熟知的一元二次方程的韦达定理.
事实上,与二次方程类似,一元三次方程也有韦达定理.
设方程有三个根,则有
证明公式,即一元三次方程的韦达定理;
已知函数恰有两个零点.
求证:的其中一个零点大于,另一个零点大于且小于;
求的取值范围.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:
函数简图如下:
,
过点,
则,
的一个解析式可以为
由题意得:即,
或
解得或
又,解得
又
故开放时间共.
16.解:
,且是的中点,则.
平面,平面,.
又平面,平面,
因为平面,
,
,则.
,,
在平面中
平面,
由知平面.
由题意得,平面,
平面.
由可知,故为坐标原点.
如图,以,,所在直线分别为,,轴,建立空间直角坐标系.
,
,.
,,,
,
由棱台的性质得,
.
由可知平面的一个法向量为,且.
直线与平面的所成角的正弦值为,
,
即,解得.
平面的一个法向量为,且.
平面的法向量为.
,,
,即
当时,,.
平面的一个法向量为.
.
平面与平面所成夹角的余弦值.
17.解:
由题意每位同学选择课外知识讲座的概率均为,则,
即的可能的取值为,
所以,,
,,
所以的分布列为:
所以;
因为,且,
所以,又,,
即,而,所以成立;
事件不相互独立,
事件课外知识讲座有同学选择,则事件课外知识讲座没有同学选择,
由可知,
所以,
事件:至少有两个课外知识讲座有同学选择,则事件:有一个课外知识讲座有同学选择,
所以,所以.
事件:至少有两个课外知识讲座有同学选择且课外知识讲座有同学选择,
分为两种情况,一种是三个课外知识讲座都有同学选择;
另一种是 两个课外知识讲座都有同学选择且课外知识讲座有同学选择,
此时或者是没有同学选择,故按照、分组即可,
故,所以,即事件不相互独立,
所以,
化简得.
18.解:
设
已知,则,
因为逆时针旋转,则,
,
,
设,
,
所以.
设,有,
因为由绕坐标原点逆时针旋转角后所得
所以,
因为,
所以,
,
所以.
设时,,由知逆时针旋转得:,
也在拋物线上,得
消得:,
有,
即,
将代入,得,
由,可知确定,则与之唯一确定.
所以讨论的个数等价于讨论方程中解除去时的非零解的个数.
令,
令,.
联立方程得,,所以时,方程有相同解:.
当时,方程均无解,所以的个数为;
当时,方程无解,仅有一个解,所以的个数为;
当时,方程无解,有一个非零解:,所以的个数为;
当或时,方程无解,有两个解,所以的个数为;
当时,方程仅有一解,有两解或,所以的个数为;
当时,方程均有两个解,且两方程不同解,所以的个数为.
综上所述:当时,的个数为;当或时,的个数为;
当或时,的个数为;当时,的个数为;
19.解:证明:因为方程有三个根,
所以方程
即为,
变形为,
比较两个方程可得.
证明:有两个零点,
有一个二重根,一个一重根,且
由可得,由可得.
由可得,.
联立上两式可得,解得,
又,
,综上.
解:由可得
.
令,
则,
,当时,,
在上单调递增,,
.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若集合,,则集合的真子集个数为( )
A. B. C. D.
2.已知向量,,若,则( )
A. B. C. D.
3.已知是直线的方向向量,是平面的法向量,若,则( )
A. B. C. D.
4.已知等差数列和的前项和分别为和,且,则( )
A. B. C. D.
5.从,,,中任取个数字,从,中任取个数字,可以组成没有重复数字的三位数的个数是( )
A. B. C. D.
6.某公司对员工的工作绩效进行评估,得到一组数据,后来复查数据时,又将重复记录在数据中,则这组新的数据和原来的数据相比,一定不会改变的是( )
A. 平均数 B. 中位数 C. 极差 D. 众数
7.抛物线绕它的对称轴旋转所得到的曲面叫抛物面,用于加热水和水壶食物的太阳灶应用了抛物线的光学性质:一束平行于抛物线对称轴的光线,经过抛物面的反射后,集中于它的焦点.已知一束平行反射镜于轴的入射光线与抛物线的交点为,则反射光线所在直线被抛物线截得的弦长为( )
A. B. C. D.
8.函数的零点个数是( )
A. B. C. D.
二、多选题:本题共3小题,共15分。在每小题给出的选项中,有多项符合题目要求。
9.如图,正方体的棱长为,则下列说法正确的是( )
A. 直线和所成的角为
B. 四面体的体积是
C. 点到平面的距离为
D. 平面与平面所成二面角的正弦值为
10.在同一平面直角坐标系中,直线与圆的位置可能为( )
A. B.
C. D.
11.把一枚质地均匀的骰子连续抛四次,设出现点数为奇数点的次数为,则下列结论中正确的是( )
A. 服从超几何分布 B. 服从二项分布
C. D. 若,则
三、填空题:本题共3小题,每小题5分,共15分。
12.已知函数,则 .
13.如图,从甲地到乙地有条路,从乙地到丁地有条路;从甲地到丙地有条路,从丙地到丁地有条路,则从甲地去丁地,共有 种不同的走法.
14.若不等式恒成立,则的最小值为 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
海水受日月的引力,在一定的时候发生涨落的现象叫潮汐,一般早潮叫潮,晚潮叫汐,潮汐具有周期现象某海滨浴场内水位单位:是时间,单位:的函数,记作,下面是某天水深的数据:
经长期观察,的曲线可近似的满足函数.
根据表中数据,作出函数简图,并求出函数一个近似表达式;
一般情况下,水深超过米该海滨浴场方可开放,另外,当水深超过米时,由于安全原因,会被关闭,那么该海滨浴场在一天内的上午:到晚上:,有多长时间可以开放?
16.本小题分
在三棱台中,平面,,且,,为的中点,是上一点,且
求证:平面;
已知,且直线与平面的所成角的正弦值为时,求平面与平面所成夹角的余弦值.
17.本小题分
名同学去听同时举行的,,课外知识讲座,每名同学只能随机选择听其中个讲座每个讲座被选择是等可能的.
记选择课外知识讲座的人数为随机变量,求的分布列与数学期望;
对于两个不相互独立的事件,,若,,称为事件,的相关系数.
已知,证明;
记事件“课外知识讲座有同学选择”,事件“至少有两个课外知识讲座有同学选择”,判断事件,是否独立,若独立,说明理由;若不独立,求.
18.本小题分
已知点为坐标原点,将向量绕逆时针旋转角后得到向量.
若,求的坐标;
若,求的坐标用表示;
若点在抛物线上,且为等边三角形,讨论的个数.
19.本小题分
设实系数一元二次方程,有两根,
则方程可变形为,展开得,
比较可以得到
这表明,任何一个一元二次方程的根与系数的关系为:两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比这就是我们熟知的一元二次方程的韦达定理.
事实上,与二次方程类似,一元三次方程也有韦达定理.
设方程有三个根,则有
证明公式,即一元三次方程的韦达定理;
已知函数恰有两个零点.
求证:的其中一个零点大于,另一个零点大于且小于;
求的取值范围.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:
函数简图如下:
,
过点,
则,
的一个解析式可以为
由题意得:即,
或
解得或
又,解得
又
故开放时间共.
16.解:
,且是的中点,则.
平面,平面,.
又平面,平面,
因为平面,
,
,则.
,,
在平面中
平面,
由知平面.
由题意得,平面,
平面.
由可知,故为坐标原点.
如图,以,,所在直线分别为,,轴,建立空间直角坐标系.
,
,.
,,,
,
由棱台的性质得,
.
由可知平面的一个法向量为,且.
直线与平面的所成角的正弦值为,
,
即,解得.
平面的一个法向量为,且.
平面的法向量为.
,,
,即
当时,,.
平面的一个法向量为.
.
平面与平面所成夹角的余弦值.
17.解:
由题意每位同学选择课外知识讲座的概率均为,则,
即的可能的取值为,
所以,,
,,
所以的分布列为:
所以;
因为,且,
所以,又,,
即,而,所以成立;
事件不相互独立,
事件课外知识讲座有同学选择,则事件课外知识讲座没有同学选择,
由可知,
所以,
事件:至少有两个课外知识讲座有同学选择,则事件:有一个课外知识讲座有同学选择,
所以,所以.
事件:至少有两个课外知识讲座有同学选择且课外知识讲座有同学选择,
分为两种情况,一种是三个课外知识讲座都有同学选择;
另一种是 两个课外知识讲座都有同学选择且课外知识讲座有同学选择,
此时或者是没有同学选择,故按照、分组即可,
故,所以,即事件不相互独立,
所以,
化简得.
18.解:
设
已知,则,
因为逆时针旋转,则,
,
,
设,
,
所以.
设,有,
因为由绕坐标原点逆时针旋转角后所得
所以,
因为,
所以,
,
所以.
设时,,由知逆时针旋转得:,
也在拋物线上,得
消得:,
有,
即,
将代入,得,
由,可知确定,则与之唯一确定.
所以讨论的个数等价于讨论方程中解除去时的非零解的个数.
令,
令,.
联立方程得,,所以时,方程有相同解:.
当时,方程均无解,所以的个数为;
当时,方程无解,仅有一个解,所以的个数为;
当时,方程无解,有一个非零解:,所以的个数为;
当或时,方程无解,有两个解,所以的个数为;
当时,方程仅有一解,有两解或,所以的个数为;
当时,方程均有两个解,且两方程不同解,所以的个数为.
综上所述:当时,的个数为;当或时,的个数为;
当或时,的个数为;当时,的个数为;
19.解:证明:因为方程有三个根,
所以方程
即为,
变形为,
比较两个方程可得.
证明:有两个零点,
有一个二重根,一个一重根,且
由可得,由可得.
由可得,.
联立上两式可得,解得,
又,
,综上.
解:由可得
.
令,
则,
,当时,,
在上单调递增,,
.
第1页,共1页
同课章节目录
