苏科版九年级数学下册 第6章 图形的相似 章节复习卷(含详解)
文档属性
| 名称 | 苏科版九年级数学下册 第6章 图形的相似 章节复习卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 915.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-03 17:37:58 | ||
图片预览




文档简介
第6章《图形的相似》章节复习卷
一、单选题(本大题共10小题,每小题3分,共30分)
1.已知,则=( )
A. B. C. D.
2.如图,在中,,,若,则( )
A. B. C. D.
3.如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为的位似图形△OCD,则点C坐标( )
A.(﹣1,﹣1) B.(﹣,﹣1) C.(﹣1,﹣) D.(﹣2,﹣1)
4.如图,在中,点分别在边上,与不平行,那么下列条件中,不能判定的是( )
A. B.
C. D.
5.的三边长分别为2,3,4,另有一个与它相似的三角形,其最长边为12,则的周长是( )
A.54 B.36 C.27 D.21
6.如图,在ABC中,D、E分别为线段BC、BA的中点,设ABC的面积为S,EBD的面积为S.则=( )
A. B. C. D.
7.如图,某零件的外径为10cm,用一个交叉卡钳(两条尺长AC和BD相等)可测量零件的内孔直径AB.如果OA:OC=OB:OD=3,且量得CD=3cm,则零件的厚度x为( )
A. B. C. D.
8.如图,在中,,高,正方形一边在上,点分别在上,交于点,则的长为( )
A. B. C. D.
9.如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( )
A. B. C. D.
10.如图,点,将线段平移得到线段,若,则点D的坐标是( )
A. B. C. D.
二、填空题(本大题共8小题,每小题4分,共32分)
11.如图,直线l1∥l2∥l3,分别交直线m、n于点A、B、C、D、E、F,若AB:BC=5:3,DE=15,则EF的长为___.
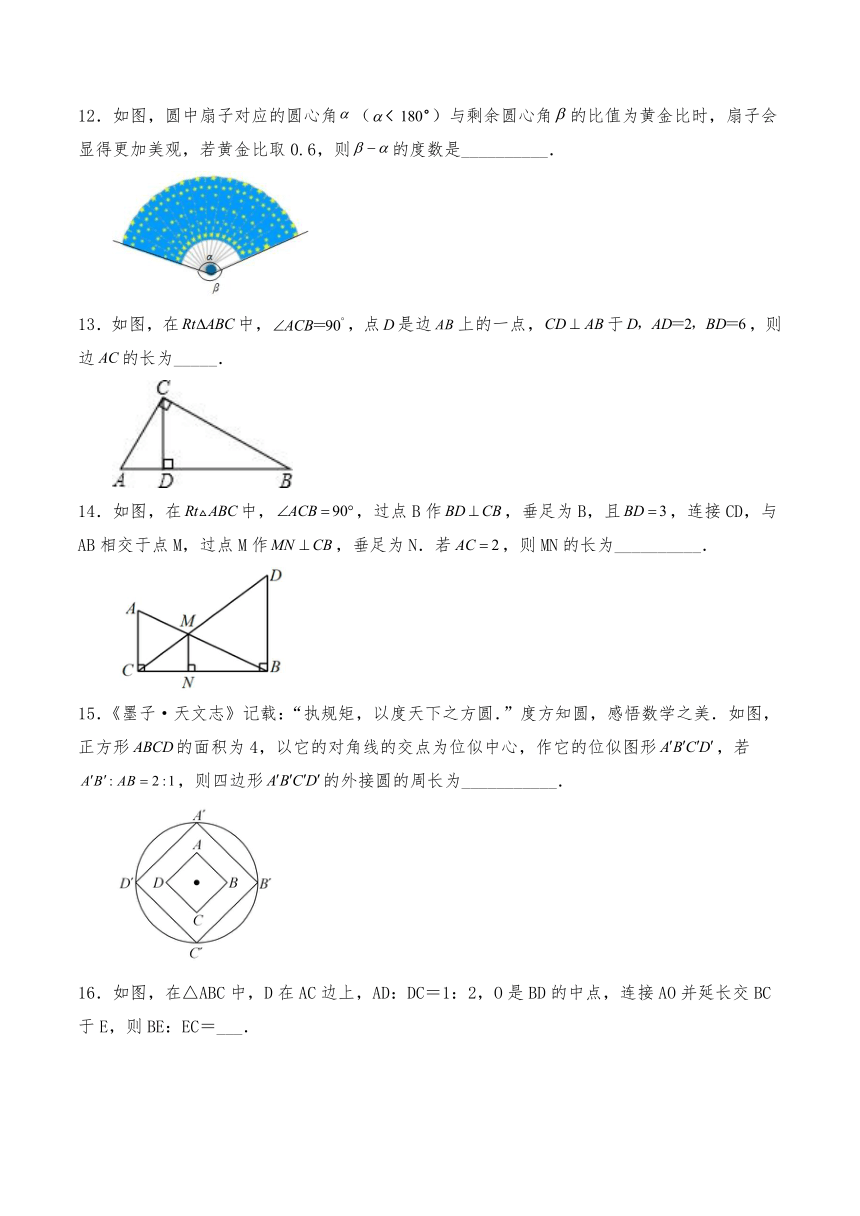
12.如图,圆中扇子对应的圆心角()与剩余圆心角的比值为黄金比时,扇子会显得更加美观,若黄金比取0.6,则的度数是__________.
13.如图,在中,,点是边上的一点,于,则边的长为_____.
14.如图,在中,,过点B作,垂足为B,且,连接CD,与AB相交于点M,过点M作,垂足为N.若,则MN的长为__________.
15.《墨子·天文志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形的面积为4,以它的对角线的交点为位似中心,作它的位似图形,若,则四边形的外接圆的周长为___________.
16.如图,在△ABC中,D在AC边上,AD:DC=1:2,O是BD的中点,连接AO并延长交BC于E,则BE:EC=___.
17.如图,矩形ABCD中,AB=2,BC=,E为CD的中点,连接AE、BD交于点P,过点P作PQ⊥BC于点Q,则PQ=_____.
18.如图,四边形ABCD中,AD∥BC,对角线AC,BD交于点O,已知,则_________.
三、解答题(本大题共6小题,共58分)
19.(8分)如图,在△ABC中,BD、CE分别是AC、AB上的中线,BD与CE相交于点O.
(1)利用尺规作图取线段CO的中点.(保留作图痕迹,不写作法);
(2)猜想CO与OE的长度有什么关系,并说明理由.
20.(8分)如图,点D是△ABC的边AB上一点,∠ABC=∠ACD.
求证:△ABC∽△ACD;
当AD=2,AB=3时,求AC的长.
21.(10分)如图,在平行四边形ABCD中,BC=8,点E、F是对角线BD上的两点,且BE=EF=FD,AE的延长线交BC于点G,GF的延长线交AD于点H.
(1)求HD的长;
(2)设的面积为a,求四边形AEFH的面积.(用含a的代数式表示)
22.(10分)如图,利用标杆测量楼高,点A,D,B在同一直线上,,,垂足分别为E,C.若测得,,,楼高是多少?
23.(10分)如图,AC是⊙O的直径,弦BD交AC于点E,点F为BD延长线上一点,∠DAF=∠B.
求证:AF是⊙O的切线;
若⊙O的半径为5,AD是AEF的中线,且AD=6,求AE的长.
24.(12分)如图,折叠矩形OABC的一边BC,使点C落在OA边的点D处,已知折痕BE=5,且,以O为原点,OA所在的直线为x轴建立如图所示的平面直角坐标系,抛物线l:y=-+c经过点E,且与AB边相交于点F.
(1)求证:△ABD∽△ODE;
(2)若M是BE的中点,连接MF,求证:MF⊥BD;
(3)P是线段BC上一点,点Q在抛物线l上,且始终满足PD⊥DQ,在点P运动过程中,能否使得PD=DQ?若能,求出所有符合条件的Q点坐标;若不能,请说明理由.
答案
一、单选题
1.D
【分析】由题意易得,进而问题可求解.
解:由可得:,
∴;
故选D.
2.C
【分析】由,,可得再建立方程即可.
解: ,,
,
解得:经检验符合题意
故选C
3.B
【分析】根据关于以原点为位似中心的对应点的坐标的关系,把A点的横纵坐标都乘以即可.
解:∵以点O为位似中心,位似比为,
而A (4,3),
∴A点的对应点C的坐标为(,﹣1).
故选:B.
4.C
【分析】根据相似三角形的判定定理逐项判断即可求解.
解:根据题意得:∠A=∠A,
A、,可利用两角对应相等的两个三角形相似,故本选项不符合题意;
B、,可利用两角对应相等的两个三角形相似,故本选项不符合题意;
C、,不能判定两个三角形相似,故本选项符合题意;
D、,可利用两边对应成比例,及其夹角对应相等的两个三角形相似,故本选项不符合题意;
故选:C
5.C
【分析】根据相似三角形的性质求解即可.
解:∵△ABC与△DEF相似,△ABC的最长边为4,△DEF的最长边为12,
∴两个相似三角形的相似比为1:3,
∴△DEF的周长与△ABC的周长比为3:1,
∴△DEF的周长为3×(2+3+4)=27,
故选:C.
6.B
【分析】先判定,得到相似比为,再根据两个相似三角形的面积比等于相似比的平方,据此解题即可.
解:∵D、E分别为线段BC、BA的中点,
∴,
又∵,
∴,相似比为,
∴,
故选:B.
7.B
【分析】求出△AOB和△COD相似,利用相似三角形对应边成比例列式计算求出AB,再根据外径的长度解答.
解:∵OA:OC=OB:OD=3,∠AOB=∠COD,
∴△AOB∽△COD,
∴AB:CD=3,
∴AB:3=3,
∴AB=9(cm),
∵外径为10cm,
∴19+2x=10,
∴x=0.5(cm).
故选:B.
8.B
【分析】证明△AEF∽△ABC,根据相似三角形对应边上的高线的比等于相似比即可求得.
解:∵四边形EFGH是正方形,
∴EF∥BC,
∴△AEF∽△ABC,
∴.
设AN=x,则EF=FG=DN=60-x,
∴
解得:x=20
所以,AN=20.
故选:B.
9.C
【分析】根据平行线分线段成比例定理即可判断A,根据相似三角形的性质即可判断B、C、D.
解:∵,
∴,△DEF∽△CBF,△ADE∽△ABC,故A不符合题意;
∴,,故B不符合题意,C符合题意;
∴,故D不符合题意;
故选C.
10.D
【分析】先过点C做出轴垂线段CE,根据相似三角形找出点C的坐标,再根据平移的性质计算出对应D点的坐标.
解:
如图过点C作轴垂线,垂足为点E,
∵
∴
∵
∴∠ABO=∠BCE
在和中,
,
∴,
∴ ,
则 ,
∵点C是由点B向右平移6个单位,向上平移2个单位得到,
∴点D同样是由点A向右平移6个单位,向上平移2个单位得到,
∵点A坐标为(0,3),
∴点D坐标为(6,5),选项D符合题意,
故答案选D
11.9
【分析】直接根据平行线分线段成比例定理求解即可.
解:∵直线l1∥l2∥l3,
∴根据平行线分线段成比例定理可得:
∴,
解得:,
经检验,是上述分式方程的解,
故答案为:9.
12.90°
【分析】根据题意得出α=0.6β,结合图形得出β=225°,然后求解即可.
解:由题意可得:α:β=0.6,即α=0.6β,
∵α+β=360°,
∴0.6β+β=360°,
解得:β=225°,
∴α=360°-225°=135°,
∴β -α=90°,
故答案为:90°.
13.4.
【分析】根据射影定理列式计算即可.
解:由射影定理得,,
解得:,
故答案为.
14.
【分析】根据MN⊥BC,AC⊥BC,DB⊥BC,得 BNM: BCA, CNM: ABD ,可得,因为,列出关于MN的方程,即可求出MN的长.
解:∵MN⊥BC,DB⊥BC,
∴AC∥MN∥DB,
∴ BNM: BCA, CNM: ABD ,
∴
即,
又∵,
∴,
解得,
故填:.
15.
【分析】根据正方形ABCD的面积为4,求出,根据位似比求出,周长即可得出;
解:正方形ABCD的面积为4,
,
,
,
,
所求周长;
故答案为:.
16.1:3
【分析】作DFAE交BC于F,如图,利用OE∥DF得到=1,所以BE=EF,利用DFAE得到=,所以CF=2EF,然后计算BE:EC.
解:作DFAE交BC于F,如图,
∵OEDF,
∴=1,
即BE=EF,
∵DFAE,
∴=,
∴CF=2EF,
∴BE:EC=BE:3BE=1:3
故答案为1:3.
17.
【分析】根据矩形的性质得到AB∥CD,AB=CD,AD=BC,∠BAD=90°,根据线段中点的定义得到DE=CD=AB,根据相似三角形的判定证明△ABP∽△EDP,再利用相识三角形的性质和判定即可得到结论.
解:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,AD=BC,∠BAD=90° ,
∵E为CD的中点,
∴DE=CD=AB,
∴△ABP∽△EDP,
∴=,
∴=,
∴=,
∵PQ⊥BC,
∴PQ∥CD,
∴△BPQ∽△DBC,
∴==,
∵CD=2,
∴PQ=,
故答案为:.
18.
【分析】先根据等高的两个三角形的面积比等于边长比,得出,再根据△AOD∽△COB得出,再根据等高的两个三角形的面积比等于边长比计算即可
解:作AE⊥BC,CF⊥BD
∵
∴△ABD和△BCD等高,高均为AE
∴
∵AD∥BC
∴△AOD∽△COB
∴
∵△BOC和△DOC等高,高均为CF
∴
∴
故答案为:
三、解答题
19.
解:(1)如图,点即为所求;
(2).
理由:连接.如图,
、分别是、上的中线,
为的中位线,
,,
,
.
20.
(1)证明:∵∠ABC=∠ACD,∠A=∠A,
∴△ABC∽△ACD;
(2)解:∵△ABC∽△ACD,
∴,即,
∴AC=(负值已舍).
∴AC的长为.
21.
解:(1)∵平行四边形ABCD,BC=8,
∴,=8,
∴,,
∴,,
∵BE=EF=FD,
∴,,
∴BG=AD=4,HD=BG,
∴HD=2;
(2)∵BE=EF,
∴=a,
∴,
∵,,,,
∴,,
∴四边形AEFH的面积=-=.
22.
解:∵,,
∴m,
∵,,
∴∥,
∴△ADE∽△ABC,
∴,
∵,
∴,
∴;
∴楼高是9米.
23.
(1)证明:∵AC是直径,
∴∠ADC=90°,
∴∠ACD+∠DAC=90°,
∵∠ACD=∠B,∠B=∠DAF,
∴∠DAF=∠ACD,
∴∠DAF+∠DAC=90°,
∴,
∵AC是直径,
∴AF是⊙O的切线;
(2)
解:作于点H,
∵⊙O的半径为5,
∴AC=10,
∵∠AHD=∠ADC=90°,∠DAH=∠CAD,
∴△ADH~△ACD,
∴,
∴,
∵AD=6,
∴,
∵AD是△AEF的中线,∠EAF=90°,
∴AD=ED,
.
24.
(1)证明:∵四边形ABCO为矩形,且由折叠的性质可知△BCE≌△BDE,
∴∠BDE=∠BCE=90°,
∵∠BAD=90°,
∴∠EDO+∠BDA=∠BDA+∠DAB=90°,
∴∠EDO=∠DBA,且∠EOD=∠BAD=90°,
∴△ABD∽△ODE;
(2)证明:∵,
∴设OD=4x,OE=3x,则DE=5x,
∴CE=DE=5x,
∴AB=OC=CE+OE=8x,
又∵△ABD∽△ODE,
∴,
∴DA=6x,
∴BC=OA=10x,
在Rt△BCE中,由勾股定理可得,即,解得x=1,
∴OE=3,OD=4,DA=6,AB=8,OA=10,∴抛物线解析式为y=﹣+3,
当x=10时,代入可得y=,
∴AF=,BF=AB﹣AF=8﹣=,
在Rt△AFD中,由勾股定理可得DF=
∴BF=DF,
又M为Rt△BDE斜边上的中点,
∴MD=MB,
∴MF为线段BD的垂直平分线,
∴MF⊥BD;
(3)解:由(2)可知抛物线解析式为y=﹣+3,设抛物线与x轴的两个交点为M、N,
令y=0,可得0=﹣+3,解得x=﹣4或x=12,
∴M(﹣4,0),N(12,0),
过D作DG⊥BC于点G,如图所示,
则DG=DM=DN=8,
∴点M、N即为满足条件的Q点,
∴存在满足条件的Q点,其坐标为(﹣4,0)或(12,0).
一、单选题(本大题共10小题,每小题3分,共30分)
1.已知,则=( )
A. B. C. D.
2.如图,在中,,,若,则( )
A. B. C. D.
3.如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为的位似图形△OCD,则点C坐标( )
A.(﹣1,﹣1) B.(﹣,﹣1) C.(﹣1,﹣) D.(﹣2,﹣1)
4.如图,在中,点分别在边上,与不平行,那么下列条件中,不能判定的是( )
A. B.
C. D.
5.的三边长分别为2,3,4,另有一个与它相似的三角形,其最长边为12,则的周长是( )
A.54 B.36 C.27 D.21
6.如图,在ABC中,D、E分别为线段BC、BA的中点,设ABC的面积为S,EBD的面积为S.则=( )
A. B. C. D.
7.如图,某零件的外径为10cm,用一个交叉卡钳(两条尺长AC和BD相等)可测量零件的内孔直径AB.如果OA:OC=OB:OD=3,且量得CD=3cm,则零件的厚度x为( )
A. B. C. D.
8.如图,在中,,高,正方形一边在上,点分别在上,交于点,则的长为( )
A. B. C. D.
9.如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( )
A. B. C. D.
10.如图,点,将线段平移得到线段,若,则点D的坐标是( )
A. B. C. D.
二、填空题(本大题共8小题,每小题4分,共32分)
11.如图,直线l1∥l2∥l3,分别交直线m、n于点A、B、C、D、E、F,若AB:BC=5:3,DE=15,则EF的长为___.
12.如图,圆中扇子对应的圆心角()与剩余圆心角的比值为黄金比时,扇子会显得更加美观,若黄金比取0.6,则的度数是__________.
13.如图,在中,,点是边上的一点,于,则边的长为_____.
14.如图,在中,,过点B作,垂足为B,且,连接CD,与AB相交于点M,过点M作,垂足为N.若,则MN的长为__________.
15.《墨子·天文志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形的面积为4,以它的对角线的交点为位似中心,作它的位似图形,若,则四边形的外接圆的周长为___________.
16.如图,在△ABC中,D在AC边上,AD:DC=1:2,O是BD的中点,连接AO并延长交BC于E,则BE:EC=___.
17.如图,矩形ABCD中,AB=2,BC=,E为CD的中点,连接AE、BD交于点P,过点P作PQ⊥BC于点Q,则PQ=_____.
18.如图,四边形ABCD中,AD∥BC,对角线AC,BD交于点O,已知,则_________.
三、解答题(本大题共6小题,共58分)
19.(8分)如图,在△ABC中,BD、CE分别是AC、AB上的中线,BD与CE相交于点O.
(1)利用尺规作图取线段CO的中点.(保留作图痕迹,不写作法);
(2)猜想CO与OE的长度有什么关系,并说明理由.
20.(8分)如图,点D是△ABC的边AB上一点,∠ABC=∠ACD.
求证:△ABC∽△ACD;
当AD=2,AB=3时,求AC的长.
21.(10分)如图,在平行四边形ABCD中,BC=8,点E、F是对角线BD上的两点,且BE=EF=FD,AE的延长线交BC于点G,GF的延长线交AD于点H.
(1)求HD的长;
(2)设的面积为a,求四边形AEFH的面积.(用含a的代数式表示)
22.(10分)如图,利用标杆测量楼高,点A,D,B在同一直线上,,,垂足分别为E,C.若测得,,,楼高是多少?
23.(10分)如图,AC是⊙O的直径,弦BD交AC于点E,点F为BD延长线上一点,∠DAF=∠B.
求证:AF是⊙O的切线;
若⊙O的半径为5,AD是AEF的中线,且AD=6,求AE的长.
24.(12分)如图,折叠矩形OABC的一边BC,使点C落在OA边的点D处,已知折痕BE=5,且,以O为原点,OA所在的直线为x轴建立如图所示的平面直角坐标系,抛物线l:y=-+c经过点E,且与AB边相交于点F.
(1)求证:△ABD∽△ODE;
(2)若M是BE的中点,连接MF,求证:MF⊥BD;
(3)P是线段BC上一点,点Q在抛物线l上,且始终满足PD⊥DQ,在点P运动过程中,能否使得PD=DQ?若能,求出所有符合条件的Q点坐标;若不能,请说明理由.
答案
一、单选题
1.D
【分析】由题意易得,进而问题可求解.
解:由可得:,
∴;
故选D.
2.C
【分析】由,,可得再建立方程即可.
解: ,,
,
解得:经检验符合题意
故选C
3.B
【分析】根据关于以原点为位似中心的对应点的坐标的关系,把A点的横纵坐标都乘以即可.
解:∵以点O为位似中心,位似比为,
而A (4,3),
∴A点的对应点C的坐标为(,﹣1).
故选:B.
4.C
【分析】根据相似三角形的判定定理逐项判断即可求解.
解:根据题意得:∠A=∠A,
A、,可利用两角对应相等的两个三角形相似,故本选项不符合题意;
B、,可利用两角对应相等的两个三角形相似,故本选项不符合题意;
C、,不能判定两个三角形相似,故本选项符合题意;
D、,可利用两边对应成比例,及其夹角对应相等的两个三角形相似,故本选项不符合题意;
故选:C
5.C
【分析】根据相似三角形的性质求解即可.
解:∵△ABC与△DEF相似,△ABC的最长边为4,△DEF的最长边为12,
∴两个相似三角形的相似比为1:3,
∴△DEF的周长与△ABC的周长比为3:1,
∴△DEF的周长为3×(2+3+4)=27,
故选:C.
6.B
【分析】先判定,得到相似比为,再根据两个相似三角形的面积比等于相似比的平方,据此解题即可.
解:∵D、E分别为线段BC、BA的中点,
∴,
又∵,
∴,相似比为,
∴,
故选:B.
7.B
【分析】求出△AOB和△COD相似,利用相似三角形对应边成比例列式计算求出AB,再根据外径的长度解答.
解:∵OA:OC=OB:OD=3,∠AOB=∠COD,
∴△AOB∽△COD,
∴AB:CD=3,
∴AB:3=3,
∴AB=9(cm),
∵外径为10cm,
∴19+2x=10,
∴x=0.5(cm).
故选:B.
8.B
【分析】证明△AEF∽△ABC,根据相似三角形对应边上的高线的比等于相似比即可求得.
解:∵四边形EFGH是正方形,
∴EF∥BC,
∴△AEF∽△ABC,
∴.
设AN=x,则EF=FG=DN=60-x,
∴
解得:x=20
所以,AN=20.
故选:B.
9.C
【分析】根据平行线分线段成比例定理即可判断A,根据相似三角形的性质即可判断B、C、D.
解:∵,
∴,△DEF∽△CBF,△ADE∽△ABC,故A不符合题意;
∴,,故B不符合题意,C符合题意;
∴,故D不符合题意;
故选C.
10.D
【分析】先过点C做出轴垂线段CE,根据相似三角形找出点C的坐标,再根据平移的性质计算出对应D点的坐标.
解:
如图过点C作轴垂线,垂足为点E,
∵
∴
∵
∴∠ABO=∠BCE
在和中,
,
∴,
∴ ,
则 ,
∵点C是由点B向右平移6个单位,向上平移2个单位得到,
∴点D同样是由点A向右平移6个单位,向上平移2个单位得到,
∵点A坐标为(0,3),
∴点D坐标为(6,5),选项D符合题意,
故答案选D
11.9
【分析】直接根据平行线分线段成比例定理求解即可.
解:∵直线l1∥l2∥l3,
∴根据平行线分线段成比例定理可得:
∴,
解得:,
经检验,是上述分式方程的解,
故答案为:9.
12.90°
【分析】根据题意得出α=0.6β,结合图形得出β=225°,然后求解即可.
解:由题意可得:α:β=0.6,即α=0.6β,
∵α+β=360°,
∴0.6β+β=360°,
解得:β=225°,
∴α=360°-225°=135°,
∴β -α=90°,
故答案为:90°.
13.4.
【分析】根据射影定理列式计算即可.
解:由射影定理得,,
解得:,
故答案为.
14.
【分析】根据MN⊥BC,AC⊥BC,DB⊥BC,得 BNM: BCA, CNM: ABD ,可得,因为,列出关于MN的方程,即可求出MN的长.
解:∵MN⊥BC,DB⊥BC,
∴AC∥MN∥DB,
∴ BNM: BCA, CNM: ABD ,
∴
即,
又∵,
∴,
解得,
故填:.
15.
【分析】根据正方形ABCD的面积为4,求出,根据位似比求出,周长即可得出;
解:正方形ABCD的面积为4,
,
,
,
,
所求周长;
故答案为:.
16.1:3
【分析】作DFAE交BC于F,如图,利用OE∥DF得到=1,所以BE=EF,利用DFAE得到=,所以CF=2EF,然后计算BE:EC.
解:作DFAE交BC于F,如图,
∵OEDF,
∴=1,
即BE=EF,
∵DFAE,
∴=,
∴CF=2EF,
∴BE:EC=BE:3BE=1:3
故答案为1:3.
17.
【分析】根据矩形的性质得到AB∥CD,AB=CD,AD=BC,∠BAD=90°,根据线段中点的定义得到DE=CD=AB,根据相似三角形的判定证明△ABP∽△EDP,再利用相识三角形的性质和判定即可得到结论.
解:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,AD=BC,∠BAD=90° ,
∵E为CD的中点,
∴DE=CD=AB,
∴△ABP∽△EDP,
∴=,
∴=,
∴=,
∵PQ⊥BC,
∴PQ∥CD,
∴△BPQ∽△DBC,
∴==,
∵CD=2,
∴PQ=,
故答案为:.
18.
【分析】先根据等高的两个三角形的面积比等于边长比,得出,再根据△AOD∽△COB得出,再根据等高的两个三角形的面积比等于边长比计算即可
解:作AE⊥BC,CF⊥BD
∵
∴△ABD和△BCD等高,高均为AE
∴
∵AD∥BC
∴△AOD∽△COB
∴
∵△BOC和△DOC等高,高均为CF
∴
∴
故答案为:
三、解答题
19.
解:(1)如图,点即为所求;
(2).
理由:连接.如图,
、分别是、上的中线,
为的中位线,
,,
,
.
20.
(1)证明:∵∠ABC=∠ACD,∠A=∠A,
∴△ABC∽△ACD;
(2)解:∵△ABC∽△ACD,
∴,即,
∴AC=(负值已舍).
∴AC的长为.
21.
解:(1)∵平行四边形ABCD,BC=8,
∴,=8,
∴,,
∴,,
∵BE=EF=FD,
∴,,
∴BG=AD=4,HD=BG,
∴HD=2;
(2)∵BE=EF,
∴=a,
∴,
∵,,,,
∴,,
∴四边形AEFH的面积=-=.
22.
解:∵,,
∴m,
∵,,
∴∥,
∴△ADE∽△ABC,
∴,
∵,
∴,
∴;
∴楼高是9米.
23.
(1)证明:∵AC是直径,
∴∠ADC=90°,
∴∠ACD+∠DAC=90°,
∵∠ACD=∠B,∠B=∠DAF,
∴∠DAF=∠ACD,
∴∠DAF+∠DAC=90°,
∴,
∵AC是直径,
∴AF是⊙O的切线;
(2)
解:作于点H,
∵⊙O的半径为5,
∴AC=10,
∵∠AHD=∠ADC=90°,∠DAH=∠CAD,
∴△ADH~△ACD,
∴,
∴,
∵AD=6,
∴,
∵AD是△AEF的中线,∠EAF=90°,
∴AD=ED,
.
24.
(1)证明:∵四边形ABCO为矩形,且由折叠的性质可知△BCE≌△BDE,
∴∠BDE=∠BCE=90°,
∵∠BAD=90°,
∴∠EDO+∠BDA=∠BDA+∠DAB=90°,
∴∠EDO=∠DBA,且∠EOD=∠BAD=90°,
∴△ABD∽△ODE;
(2)证明:∵,
∴设OD=4x,OE=3x,则DE=5x,
∴CE=DE=5x,
∴AB=OC=CE+OE=8x,
又∵△ABD∽△ODE,
∴,
∴DA=6x,
∴BC=OA=10x,
在Rt△BCE中,由勾股定理可得,即,解得x=1,
∴OE=3,OD=4,DA=6,AB=8,OA=10,∴抛物线解析式为y=﹣+3,
当x=10时,代入可得y=,
∴AF=,BF=AB﹣AF=8﹣=,
在Rt△AFD中,由勾股定理可得DF=
∴BF=DF,
又M为Rt△BDE斜边上的中点,
∴MD=MB,
∴MF为线段BD的垂直平分线,
∴MF⊥BD;
(3)解:由(2)可知抛物线解析式为y=﹣+3,设抛物线与x轴的两个交点为M、N,
令y=0,可得0=﹣+3,解得x=﹣4或x=12,
∴M(﹣4,0),N(12,0),
过D作DG⊥BC于点G,如图所示,
则DG=DM=DN=8,
∴点M、N即为满足条件的Q点,
∴存在满足条件的Q点,其坐标为(﹣4,0)或(12,0).
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
