25.2 用列举法求概率 同步练习(含答案) 2024—2025学年人教版数学九年级上册
文档属性
| 名称 | 25.2 用列举法求概率 同步练习(含答案) 2024—2025学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 351.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-03 00:00:00 | ||
图片预览



文档简介
25.2 用列举法求概率
中小学教育资源及组卷应用平台
第1课时 运用直接列举或列表法求概率
A层
知识点一 用直接列举法求概率
1.从长度分别为 1cm、3cm、5cm、6 cm的四条线段中随机取出三条,则能够组成三角形的概率为 ( )
A. B. C. D.
2.小亮、小莹、大刚三位同学随机地站成一排合影留念,小亮恰好站在中间的概率是 ( )
A. B. C. D.
3.一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都会随机选择其中 蚂蚁一条路径,则它遇到食物的概率是 .
4.如图,数轴上的点A,B,C,D 表示的数分别为-3,-1,1,2,从A,B,C,D 四点中任意取两点,求所取两点之间的距离为 2 的概率.
知识点二 用列表法求概率
5.有一枚质地均匀的正方体骰子,六个面上分别刻有1到6 的点数.将它投掷两次,则两次掷得骰子朝上一面的点数之和为5 的概率是 ( )
A. B. C. D.
6.从1,2,3,4 中任取两个不同的数,分别记为a和b,则 的概率是 ( )
A. B. C. D.
7.从-2,4,5这3个数中任取两个数作为点 P 的坐标,则点 P 在第四象限的概率是 .
8.甲、乙两人都握有分别标记为 A,B,C 的三张牌,两人做游戏,游戏规则是:若两人出的牌不同,则 A 胜 B,B 胜C,C 胜A;若两人出的牌相同,则为平局.
(1)用列表法表示出甲、乙两人一次游戏的所有可能的结果;
(2)求出现平局的概率.
B层
9.若十位上的数字比个位上的数字和百位上的数字都大的三位数叫做“中高数”,如796 就是一个“中高数”.若十位上数字为7,则从 3,4,5,6,8,9 中任选不同的两数,与 7 组成“中高数”的概率是 ( )
A. B. C. D.
10.如图,在三条横线和三条竖线组成的图形中,任选两条横线和两条竖线都可以围成一个矩形,从这些矩形中任选一个,则所选矩形含点 A 的概率是 ( )
A. B. C. D.
A
11.看了《田忌赛马》故事后,小杨用数学模型来分析:齐王与田忌的上中下三个等级的三匹马记分如表,每匹马只赛一场,两数相比,大数为胜,三场两胜则赢.已知齐王的三匹马出场顺序为10,8,6.若田忌的三匹马随机出场,则田忌能赢得比赛的概率为 .
马匹 姓名 下等马 中等马 上等马
齐王 6 8 10
田忌 5 7 9
12.如图所示,甲、乙两人在玩转盘游戏时,分别把转盘A,B 分成3等份和4等份,并在每一份内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所在区域的数字之积为奇数时,甲获胜;当数字之积为偶数时,乙获胜.如果指针恰好在分割线上时,则需重新转动转盘.
(1)利用列表的方法,求甲获胜的概率;
(2)这个游戏规则对甲、乙双方公平吗 若公平,请说明理由;若不公平,请你在转盘A上只修改一个数字使游戏公平(不需要说明理由).
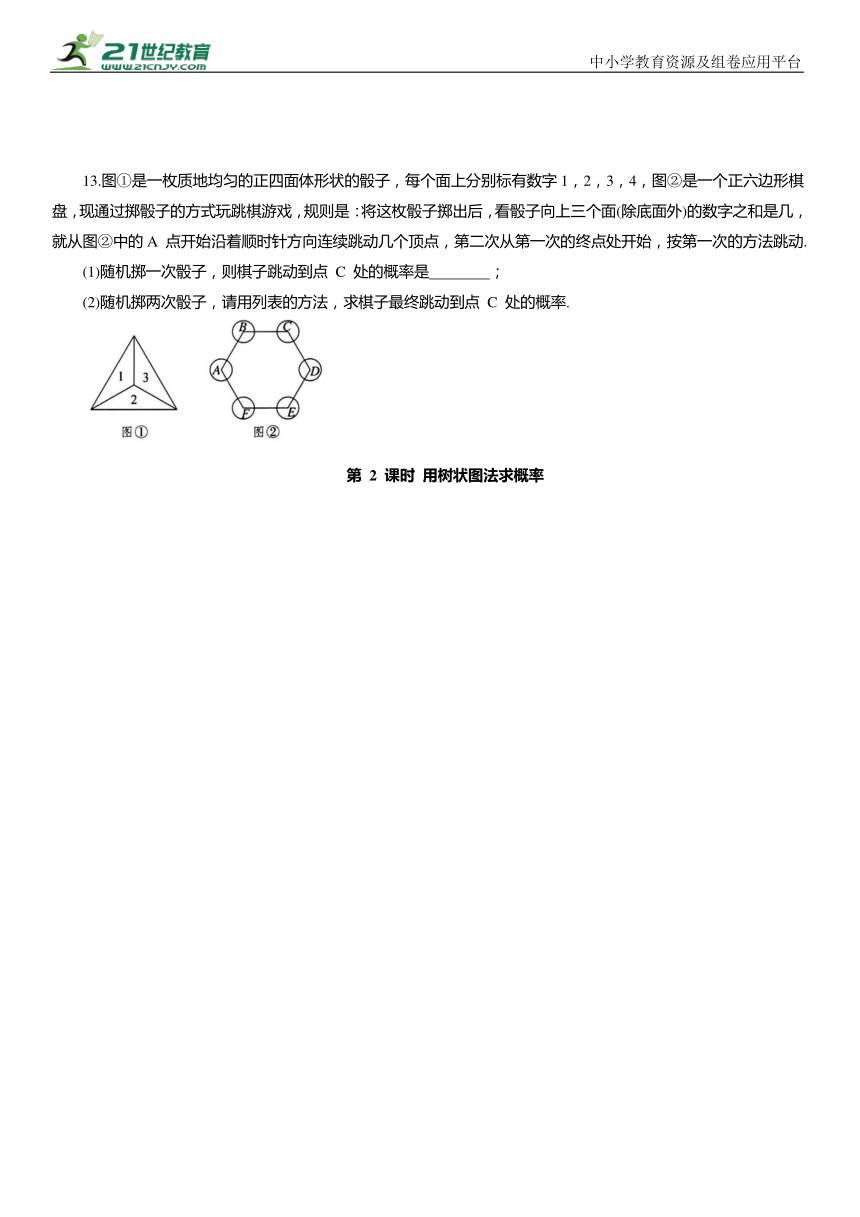
13.图①是一枚质地均匀的正四面体形状的骰子,每个面上分别标有数字1,2,3,4,图②是一个正六边形棋盘,现通过掷骰子的方式玩跳棋游戏,规则是:将这枚骰子掷出后,看骰子向上三个面(除底面外)的数字之和是几,就从图②中的A 点开始沿着顺时针方向连续跳动几个顶点,第二次从第一次的终点处开始,按第一次的方法跳动.
(1)随机掷一次骰子,则棋子跳动到点 C 处的概率是 ;
(2)随机掷两次骰子,请用列表的方法,求棋子最终跳动到点 C 处的概率.
第 2 课时 用树状图法求概率
A层
知识点一 用树状图法求概率
1.不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到红球的概率为 ( )
A B. C. D.
2.经过某路口的汽车,可能直行,也可能左拐或右拐.假设这三种可能性相同,现有两车经过该路口,恰好有一车直行,另一车左拐的概率为 ( )
A. B. C. D.
3.有4张看上去无差别的卡片,上面分别写着2,3,4,6,小红随机抽取 1张后,放回并混在一起,再随机抽取 1张,则小红第二次取出的数字能够整除第一次 取 出的数 字的概 率 为
4.甲、乙、丙三人各自随机选择到A,B 两个献血站进行爱心献血.求这三人在同一个献血站献血的概率.
知识点二 树状图法与列表法的灵活运用
5.在排球训练中,甲、乙、丙三人相互传球,由甲开始发球(记为第一次传球),则经过三次传球后,球仍回到甲手中的概率是 ( )
A. B. C. D.
6.学校团委在“五四”青年节举行“感动校园十大人物”颁奖活动,九(4)班决定从甲、乙、丙、丁四人中随机派两名代表参加此活动,则甲、乙两人恰有一人参加此活动的概率是 ( )
A. B. C. D.
7.点 P 的坐标是(a,b),从-2,-1,0,1,2 这五个数中任取一个数作为a 的值,再从余下的四个数中任取一个数作为b 的值,则点P(a,b)在平面直角坐标系中第二象限内的概率是
8.一张圆桌旁设有 4 个座位,丙先坐在了如图所示的座位上,甲、乙2 人等可能地坐到①、②、③中的2 个座位上.
(1)甲坐在①号座位的概率是 ;
(2)用画树状图或列表的方法,求甲与乙相邻而坐的概率.
B层
9.现有4盒同一品牌的牛奶,其中 2 盒已过期,随机抽取2 盒,至少有一盒过期的概率是 ( )
A. B. C. D.
10.投掷一枚质地均匀的骰子两次(骰子的六个面上分别刻有 1 到6 的点数),向上一面的点数依次记为a,b,那么方程 有实数解的概率是 ( )
A. B. C. D.
11.一只不透明的袋子中装有1个黄球,现放若干个红球,它们与黄球除颜色外都相同,搅匀后从中任意摸出两个球,使得 P(摸出一红一黄)=P(摸出两红),则放入的红球个数为 .
12.甲口袋中装有 2个相同小球,它们分别写有数字1,2;乙口袋中装有 3个相同小球,它们分别写有数字3,4,5;丙口袋中装有2个相同小球,它们分别写有数字 6,7.从三个口袋各随机取出1个小球.用画树状图或列表法求:
(1)取出的3个小球上恰好有一个偶数的概率;
(2)取出的3个小球上全是奇数的概率.
C层
13.如图,3×3 的方格分为上、中、下三层,第一层有一枚黑色方块甲,可在方格A,B,C 中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格 D,E,F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.
(1)若乙固定在 E 处,移动黑色方块甲后构成的拼图是轴对称图形的概率是 ;
(2)若甲、乙均可在本层移动.
①用树状图或列表法求出黑色方块所构拼图是轴对称图形的概率;
②黑色方块所构拼图是中心对称图形的概率是 .
25.2 用列举法求概率
第1课时 运用直接列举或列表法求概率1. A 2. B 3.
4.解:由图可知,任取两点有 AB,BC,CD,AC,BD,AD 共6种情况,其中 AB=BC=2,∴所取两点之间的距离为 2 的概率为
5. A 6. D 7.
8.解:(1)列表如下:
甲乙 A B C
A (A,A) (B,A) (C,A)
B (A,B) (B,B) (C,B)
C (A,C) (B,C) (C,C)
则共有9种等可能的结果.
(2)∵出现平局的有(A,A),(B,B),(C,C)3种情况,∴出现平局的概率为
9. C10. D 11.
12.解:(1)列表如下:
积 -2 --3 2 3
1 -2 --3 2 3
2 --4 --6 4 6
3 --6 --9 6 9
由表可知,共有 12种等可能结果,其中指针所在区域的数字之积为奇数的有4种结果,所以甲获胜的概率为
(2)∵指针所在区域的数字之积为偶数的概率为 ∴这个游戏规则对甲、乙双方不公平.将转盘 A 上的数字 2 改为1,则游戏公平(修改方法不唯一).
13.解:(1)
(2)列表如下:
9 8 7 6
9 (9,9) (8,9) (7,9) (6,9)
8 (9,8) (8,8) (7,8) (6,8)
7 (9,7) (8,7) (7,7) (6,7)
6 (9,6) (8,6) (7,6) (6,6)
共有 16种等可能的情况,和为 14 可以到达点 C,有 3 种情形,所以棋子最终跳动到点C处的概率为 .
第2 课时 用树状图法求概率
1. D 2. A 3.
4.解:画树状图如图所示:
共8种等可能情况,其中这三人在同一个献血站献血的有 2 种结果,所以这三人在同一个献血站献血的概率为
5. B 6. A 7.
8.解:((1)
(2)画树状图如图所示:
共有 6 种等可能的结果,甲与乙两同学恰好相邻而坐的结果有4种,∴甲与乙相邻而坐的概率为
9. D 10. D 1 1.3
12.解:(1)画树状图为:
共有 12 种等可能的结果,其中取出的3 个小球上恰好有一个偶数的结果数为5,所以取出的3个小球上恰好有一个偶数的概率为 .
(2)取出的3个小球上全是奇数的结果数为2,所以取出的3个小球上全是奇数的概率为
13.解:(1)
(2)①画树状图如下:
由树状图可知,一共有9种等可能的结果,其中有 5 种所构拼图是轴对称图形,则黑色方块所构拼图是轴对称图形的概率为 .
②
中小学教育资源及组卷应用平台
第1课时 运用直接列举或列表法求概率
A层
知识点一 用直接列举法求概率
1.从长度分别为 1cm、3cm、5cm、6 cm的四条线段中随机取出三条,则能够组成三角形的概率为 ( )
A. B. C. D.
2.小亮、小莹、大刚三位同学随机地站成一排合影留念,小亮恰好站在中间的概率是 ( )
A. B. C. D.
3.一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都会随机选择其中 蚂蚁一条路径,则它遇到食物的概率是 .
4.如图,数轴上的点A,B,C,D 表示的数分别为-3,-1,1,2,从A,B,C,D 四点中任意取两点,求所取两点之间的距离为 2 的概率.
知识点二 用列表法求概率
5.有一枚质地均匀的正方体骰子,六个面上分别刻有1到6 的点数.将它投掷两次,则两次掷得骰子朝上一面的点数之和为5 的概率是 ( )
A. B. C. D.
6.从1,2,3,4 中任取两个不同的数,分别记为a和b,则 的概率是 ( )
A. B. C. D.
7.从-2,4,5这3个数中任取两个数作为点 P 的坐标,则点 P 在第四象限的概率是 .
8.甲、乙两人都握有分别标记为 A,B,C 的三张牌,两人做游戏,游戏规则是:若两人出的牌不同,则 A 胜 B,B 胜C,C 胜A;若两人出的牌相同,则为平局.
(1)用列表法表示出甲、乙两人一次游戏的所有可能的结果;
(2)求出现平局的概率.
B层
9.若十位上的数字比个位上的数字和百位上的数字都大的三位数叫做“中高数”,如796 就是一个“中高数”.若十位上数字为7,则从 3,4,5,6,8,9 中任选不同的两数,与 7 组成“中高数”的概率是 ( )
A. B. C. D.
10.如图,在三条横线和三条竖线组成的图形中,任选两条横线和两条竖线都可以围成一个矩形,从这些矩形中任选一个,则所选矩形含点 A 的概率是 ( )
A. B. C. D.
A
11.看了《田忌赛马》故事后,小杨用数学模型来分析:齐王与田忌的上中下三个等级的三匹马记分如表,每匹马只赛一场,两数相比,大数为胜,三场两胜则赢.已知齐王的三匹马出场顺序为10,8,6.若田忌的三匹马随机出场,则田忌能赢得比赛的概率为 .
马匹 姓名 下等马 中等马 上等马
齐王 6 8 10
田忌 5 7 9
12.如图所示,甲、乙两人在玩转盘游戏时,分别把转盘A,B 分成3等份和4等份,并在每一份内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所在区域的数字之积为奇数时,甲获胜;当数字之积为偶数时,乙获胜.如果指针恰好在分割线上时,则需重新转动转盘.
(1)利用列表的方法,求甲获胜的概率;
(2)这个游戏规则对甲、乙双方公平吗 若公平,请说明理由;若不公平,请你在转盘A上只修改一个数字使游戏公平(不需要说明理由).
13.图①是一枚质地均匀的正四面体形状的骰子,每个面上分别标有数字1,2,3,4,图②是一个正六边形棋盘,现通过掷骰子的方式玩跳棋游戏,规则是:将这枚骰子掷出后,看骰子向上三个面(除底面外)的数字之和是几,就从图②中的A 点开始沿着顺时针方向连续跳动几个顶点,第二次从第一次的终点处开始,按第一次的方法跳动.
(1)随机掷一次骰子,则棋子跳动到点 C 处的概率是 ;
(2)随机掷两次骰子,请用列表的方法,求棋子最终跳动到点 C 处的概率.
第 2 课时 用树状图法求概率
A层
知识点一 用树状图法求概率
1.不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到红球的概率为 ( )
A B. C. D.
2.经过某路口的汽车,可能直行,也可能左拐或右拐.假设这三种可能性相同,现有两车经过该路口,恰好有一车直行,另一车左拐的概率为 ( )
A. B. C. D.
3.有4张看上去无差别的卡片,上面分别写着2,3,4,6,小红随机抽取 1张后,放回并混在一起,再随机抽取 1张,则小红第二次取出的数字能够整除第一次 取 出的数 字的概 率 为
4.甲、乙、丙三人各自随机选择到A,B 两个献血站进行爱心献血.求这三人在同一个献血站献血的概率.
知识点二 树状图法与列表法的灵活运用
5.在排球训练中,甲、乙、丙三人相互传球,由甲开始发球(记为第一次传球),则经过三次传球后,球仍回到甲手中的概率是 ( )
A. B. C. D.
6.学校团委在“五四”青年节举行“感动校园十大人物”颁奖活动,九(4)班决定从甲、乙、丙、丁四人中随机派两名代表参加此活动,则甲、乙两人恰有一人参加此活动的概率是 ( )
A. B. C. D.
7.点 P 的坐标是(a,b),从-2,-1,0,1,2 这五个数中任取一个数作为a 的值,再从余下的四个数中任取一个数作为b 的值,则点P(a,b)在平面直角坐标系中第二象限内的概率是
8.一张圆桌旁设有 4 个座位,丙先坐在了如图所示的座位上,甲、乙2 人等可能地坐到①、②、③中的2 个座位上.
(1)甲坐在①号座位的概率是 ;
(2)用画树状图或列表的方法,求甲与乙相邻而坐的概率.
B层
9.现有4盒同一品牌的牛奶,其中 2 盒已过期,随机抽取2 盒,至少有一盒过期的概率是 ( )
A. B. C. D.
10.投掷一枚质地均匀的骰子两次(骰子的六个面上分别刻有 1 到6 的点数),向上一面的点数依次记为a,b,那么方程 有实数解的概率是 ( )
A. B. C. D.
11.一只不透明的袋子中装有1个黄球,现放若干个红球,它们与黄球除颜色外都相同,搅匀后从中任意摸出两个球,使得 P(摸出一红一黄)=P(摸出两红),则放入的红球个数为 .
12.甲口袋中装有 2个相同小球,它们分别写有数字1,2;乙口袋中装有 3个相同小球,它们分别写有数字3,4,5;丙口袋中装有2个相同小球,它们分别写有数字 6,7.从三个口袋各随机取出1个小球.用画树状图或列表法求:
(1)取出的3个小球上恰好有一个偶数的概率;
(2)取出的3个小球上全是奇数的概率.
C层
13.如图,3×3 的方格分为上、中、下三层,第一层有一枚黑色方块甲,可在方格A,B,C 中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格 D,E,F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.
(1)若乙固定在 E 处,移动黑色方块甲后构成的拼图是轴对称图形的概率是 ;
(2)若甲、乙均可在本层移动.
①用树状图或列表法求出黑色方块所构拼图是轴对称图形的概率;
②黑色方块所构拼图是中心对称图形的概率是 .
25.2 用列举法求概率
第1课时 运用直接列举或列表法求概率1. A 2. B 3.
4.解:由图可知,任取两点有 AB,BC,CD,AC,BD,AD 共6种情况,其中 AB=BC=2,∴所取两点之间的距离为 2 的概率为
5. A 6. D 7.
8.解:(1)列表如下:
甲乙 A B C
A (A,A) (B,A) (C,A)
B (A,B) (B,B) (C,B)
C (A,C) (B,C) (C,C)
则共有9种等可能的结果.
(2)∵出现平局的有(A,A),(B,B),(C,C)3种情况,∴出现平局的概率为
9. C10. D 11.
12.解:(1)列表如下:
积 -2 --3 2 3
1 -2 --3 2 3
2 --4 --6 4 6
3 --6 --9 6 9
由表可知,共有 12种等可能结果,其中指针所在区域的数字之积为奇数的有4种结果,所以甲获胜的概率为
(2)∵指针所在区域的数字之积为偶数的概率为 ∴这个游戏规则对甲、乙双方不公平.将转盘 A 上的数字 2 改为1,则游戏公平(修改方法不唯一).
13.解:(1)
(2)列表如下:
9 8 7 6
9 (9,9) (8,9) (7,9) (6,9)
8 (9,8) (8,8) (7,8) (6,8)
7 (9,7) (8,7) (7,7) (6,7)
6 (9,6) (8,6) (7,6) (6,6)
共有 16种等可能的情况,和为 14 可以到达点 C,有 3 种情形,所以棋子最终跳动到点C处的概率为 .
第2 课时 用树状图法求概率
1. D 2. A 3.
4.解:画树状图如图所示:
共8种等可能情况,其中这三人在同一个献血站献血的有 2 种结果,所以这三人在同一个献血站献血的概率为
5. B 6. A 7.
8.解:((1)
(2)画树状图如图所示:
共有 6 种等可能的结果,甲与乙两同学恰好相邻而坐的结果有4种,∴甲与乙相邻而坐的概率为
9. D 10. D 1 1.3
12.解:(1)画树状图为:
共有 12 种等可能的结果,其中取出的3 个小球上恰好有一个偶数的结果数为5,所以取出的3个小球上恰好有一个偶数的概率为 .
(2)取出的3个小球上全是奇数的结果数为2,所以取出的3个小球上全是奇数的概率为
13.解:(1)
(2)①画树状图如下:
由树状图可知,一共有9种等可能的结果,其中有 5 种所构拼图是轴对称图形,则黑色方块所构拼图是轴对称图形的概率为 .
②
同课章节目录
