综合滚动练习:圆的有关概念及性质 同步练习 (含答案)2024—2025学年人教版数学九年级上册
文档属性
| 名称 | 综合滚动练习:圆的有关概念及性质 同步练习 (含答案)2024—2025学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 512.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-03 05:48:37 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
综合滚动练习:圆的有关概念及性质
范围:24.1~24.2 满分:100 分
一、选择题(每小题4分,共32分)
1.已知⊙O 的半径长为5,如果点 P 在⊙O 内,那么下列结论正确的是 ( )
A. OP>5 B. OP=5
C.02.下列关于圆的说法,正确的是 ( )
A.相等的圆心角所对的弦相等
B.过圆心且平分弦的直线一定垂直于该弦
C.经过半径的端点且垂直于该半径的直线是圆的切线
D.过圆外一点引圆的两条切线,则切线长相等
3.在⊙O中,直径AB=15,弦 DE⊥AB 于点C.若 OC : OB=3:5,则 DE 的长为 ( )
A.6 B.9 C.12 D.15
4.如图为 4×4 的网格图,A,B,C,D,O 均在格点上,则点 O 是 ( )
A.△ACD 的外心 B.△ABC 的外心
C.△ACD 的内心 D.△ABC 的内心
5.如图,四边形 ABCD 是⊙O的内接四边形,BE 是⊙O 的直径,连接AE.若∠BCD=2∠BAD,则∠DAE 的度数是 ( )
A.30° B.35°
C.45° D.60°
6.如图,PA,PB 分别与⊙O 相切于A,B 两点,∠P=72°,则∠C= ( )
A.108° B.72° C.54° D.36°
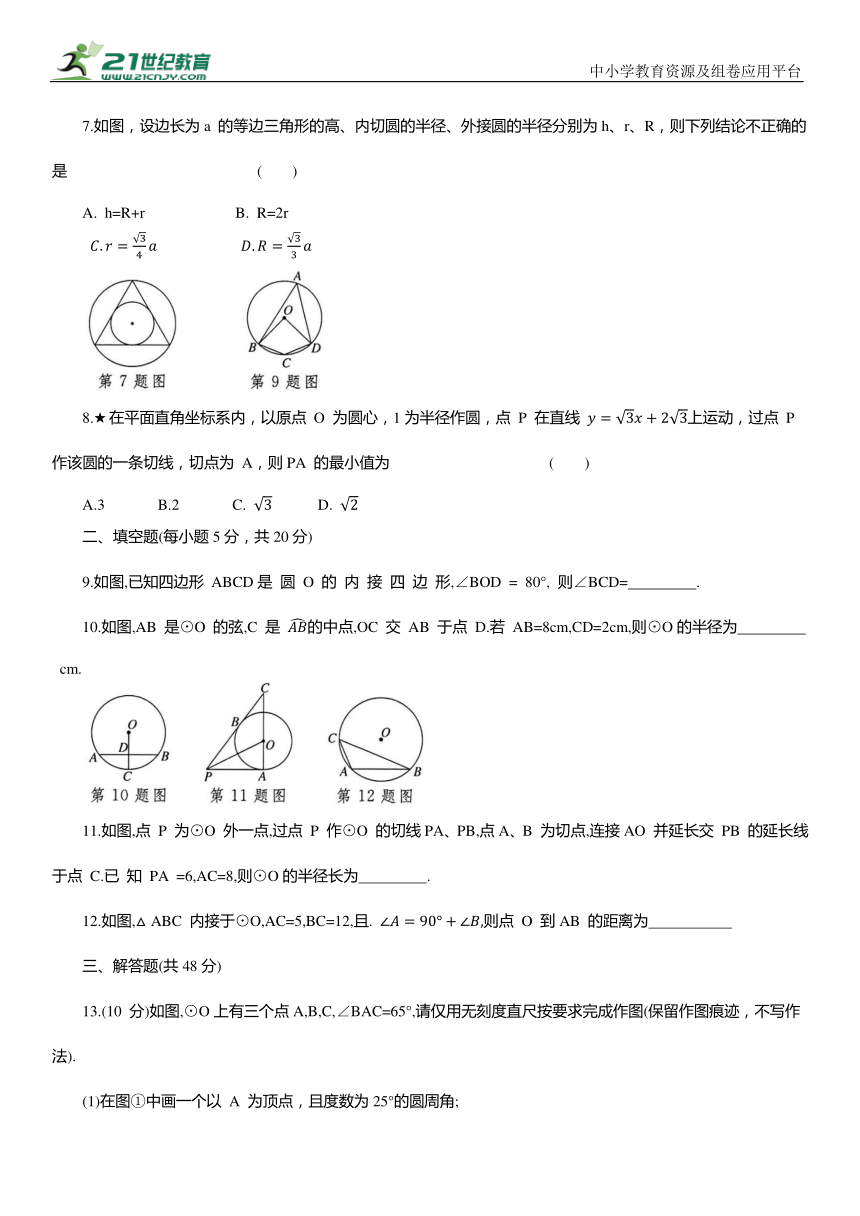
7.如图,设边长为a 的等边三角形的高、内切圆的半径、外接圆的半径分别为h、r、R,则下列结论不正确的是 ( )
A. h=R+r B. R=2r
8.★在平面直角坐标系内,以原点 O 为圆心,1为半径作圆,点 P 在直线 上运动,过点 P 作该圆的一条切线,切点为 A,则PA 的最小值为 ( )
A.3 B.2 C. D.
二、填空题(每小题5分,共20分)
9.如图,已知四边形 ABCD是 圆 O 的 内 接 四 边 形,∠BOD = 80°, 则∠BCD= .
10.如图,AB 是⊙O 的弦,C 是 的中点,OC 交 AB 于点 D.若 AB=8cm,CD=2cm,则⊙O的半径为 cm.
11.如图,点 P 为⊙O 外一点,过点 P 作⊙O 的切线PA、PB,点A、B 为切点,连接AO 并延长交 PB 的延长线于点 C.已 知 PA =6,AC=8,则⊙O的半径长为 .
12.如图,△ABC 内接于⊙O,AC=5,BC=12,且. 则点 O 到AB 的距离为
三、解答题(共48分)
13.(10 分)如图,⊙O上有三个点A,B,C,∠BAC=65°,请仅用无刻度直尺按要求完成作图(保留作图痕迹,不写作法).
(1)在图①中画一个以 A 为顶点,且度数为25°的圆周角;
(2)在图②中画一个以 B 为顶点,且度数为25°的圆周角.
14.(12分)如图,在以点 O 为圆心的两个同心圆中,大圆的弦 AB交小圆于C、D两点.
(1)求证:AD=BC;
(2)若AC=3,大圆和小圆的半径分别为 6 和4,求 CD 的长.
15.(12分)如图,AB 为⊙O的直径,C 为⊙O 上一点,D 为 的中点.过点 D 作直线AC 的垂线,垂足为E,连接OD.
(1)求证:∠A=∠DOB;
(2)DE 与⊙O 有怎样的位置关系 请说明理由.
16.(14 分)如图,AB 是⊙O的直径,过点 A 作⊙O 的切线AC,点 P 是射线 AC 上的动点,连接OP,过点 B 作 BD∥OP,交⊙O 于点D,连接 PD.
(1)求证:PD 是⊙O 的切线;
(2)当四边形 POBD 是平行四边形时,求∠APO的度数.
综合滚动练习:圆的有关概念及性质1. D 2. D 3. C 4. B 5. A 6. C 7. C
8.D 解析:如图,直线 与x 轴交于C,与y轴交于点 D,作OH⊥CD于点 H.当 x = 0 时, ∴点D 的坐标为(0,2 ).当y=0时, 解得x= -2.∴点C的坐标为(-2,0).. 连接OP,OA.∵PA为⊙O 的切线, .当OP 的值最小时,PA 的值最小,而OP 的最小值为OH 的长,∴PA 的最小值为 故选 D.
9.140° 10.5 11.3
12. 解析:如图,作直径CD,连接 BD,过 O 作OM⊥AB于M,过B 作BN⊥CD 于N,则∠CBD=90°.∵∠A= 90°+ ∠ABC, ∴∠A= ∠ABD.∴∠ABD+∠D=∠A+∠D=180°.∴CD∥AB.∴OM=BN,∠DCB=∠ABC.∴AC=BD.∴BD= AC=5.在 Rt△CBD 中,CD= 即点 O到AB 的距离为 .
13.解:(1)如图①,∠DAC 为所作.(答案不唯一)(5分)
(2)如图②,∠CBD 为所作.(10分)
14.(1)证明:如图,作OH⊥CD 于H,∴CH = DH,AH = BH.
∴AH+ DH = BH + CH. A
∴AD=BC.(6分)
(2)解:如图,连接OC.设CH=x,在Rt△OCH中, 在 Rt△OAH中,( 解得 .(12分)
15.(1)证明:连接OC.∵D 为 的中点, ∴∠A=∠DOB.(6分)
(2)解:DE 与⊙O 相切.理由如下:∵∠A=∠DOB,∴AE∥OD.∵DE⊥AE,∴OD⊥DE.∴DE 与⊙O 相切.(12分)
16.(1)证明:连接OD.∵PA 切⊙O 于 A,∴PA⊥AB,即∠PAO=90°.∵OP ∥BD,∴∠DBO=∠AOP,∠BDO = ∠DOP. ∵ OD = OB,∴∠BDO=∠DBO.∴∠DOP = ∠AOP.在△AOP 和△DOP 中 ∴△AOP ≌△DOP (SAS). ∴∠PDO =∠PAO=90°,即OD⊥PD.∵OD 是⊙O 的半径,∴PD 是⊙O 的切线.(7分)
(2)解:由(1)知△AOP≌△DOP,∴PA=PD.
∵四边形 POBD 是平行四边形,∴PD=OB.
∵OB=OA,∴PA=OA.∴∠APO=∠AOP.
∵∠PAO= 90°, ∴ ∠APO = ∠AOP = 45°.(14分)
综合滚动练习:圆的有关概念及性质
范围:24.1~24.2 满分:100 分
一、选择题(每小题4分,共32分)
1.已知⊙O 的半径长为5,如果点 P 在⊙O 内,那么下列结论正确的是 ( )
A. OP>5 B. OP=5
C.0
A.相等的圆心角所对的弦相等
B.过圆心且平分弦的直线一定垂直于该弦
C.经过半径的端点且垂直于该半径的直线是圆的切线
D.过圆外一点引圆的两条切线,则切线长相等
3.在⊙O中,直径AB=15,弦 DE⊥AB 于点C.若 OC : OB=3:5,则 DE 的长为 ( )
A.6 B.9 C.12 D.15
4.如图为 4×4 的网格图,A,B,C,D,O 均在格点上,则点 O 是 ( )
A.△ACD 的外心 B.△ABC 的外心
C.△ACD 的内心 D.△ABC 的内心
5.如图,四边形 ABCD 是⊙O的内接四边形,BE 是⊙O 的直径,连接AE.若∠BCD=2∠BAD,则∠DAE 的度数是 ( )
A.30° B.35°
C.45° D.60°
6.如图,PA,PB 分别与⊙O 相切于A,B 两点,∠P=72°,则∠C= ( )
A.108° B.72° C.54° D.36°
7.如图,设边长为a 的等边三角形的高、内切圆的半径、外接圆的半径分别为h、r、R,则下列结论不正确的是 ( )
A. h=R+r B. R=2r
8.★在平面直角坐标系内,以原点 O 为圆心,1为半径作圆,点 P 在直线 上运动,过点 P 作该圆的一条切线,切点为 A,则PA 的最小值为 ( )
A.3 B.2 C. D.
二、填空题(每小题5分,共20分)
9.如图,已知四边形 ABCD是 圆 O 的 内 接 四 边 形,∠BOD = 80°, 则∠BCD= .
10.如图,AB 是⊙O 的弦,C 是 的中点,OC 交 AB 于点 D.若 AB=8cm,CD=2cm,则⊙O的半径为 cm.
11.如图,点 P 为⊙O 外一点,过点 P 作⊙O 的切线PA、PB,点A、B 为切点,连接AO 并延长交 PB 的延长线于点 C.已 知 PA =6,AC=8,则⊙O的半径长为 .
12.如图,△ABC 内接于⊙O,AC=5,BC=12,且. 则点 O 到AB 的距离为
三、解答题(共48分)
13.(10 分)如图,⊙O上有三个点A,B,C,∠BAC=65°,请仅用无刻度直尺按要求完成作图(保留作图痕迹,不写作法).
(1)在图①中画一个以 A 为顶点,且度数为25°的圆周角;
(2)在图②中画一个以 B 为顶点,且度数为25°的圆周角.
14.(12分)如图,在以点 O 为圆心的两个同心圆中,大圆的弦 AB交小圆于C、D两点.
(1)求证:AD=BC;
(2)若AC=3,大圆和小圆的半径分别为 6 和4,求 CD 的长.
15.(12分)如图,AB 为⊙O的直径,C 为⊙O 上一点,D 为 的中点.过点 D 作直线AC 的垂线,垂足为E,连接OD.
(1)求证:∠A=∠DOB;
(2)DE 与⊙O 有怎样的位置关系 请说明理由.
16.(14 分)如图,AB 是⊙O的直径,过点 A 作⊙O 的切线AC,点 P 是射线 AC 上的动点,连接OP,过点 B 作 BD∥OP,交⊙O 于点D,连接 PD.
(1)求证:PD 是⊙O 的切线;
(2)当四边形 POBD 是平行四边形时,求∠APO的度数.
综合滚动练习:圆的有关概念及性质1. D 2. D 3. C 4. B 5. A 6. C 7. C
8.D 解析:如图,直线 与x 轴交于C,与y轴交于点 D,作OH⊥CD于点 H.当 x = 0 时, ∴点D 的坐标为(0,2 ).当y=0时, 解得x= -2.∴点C的坐标为(-2,0).. 连接OP,OA.∵PA为⊙O 的切线, .当OP 的值最小时,PA 的值最小,而OP 的最小值为OH 的长,∴PA 的最小值为 故选 D.
9.140° 10.5 11.3
12. 解析:如图,作直径CD,连接 BD,过 O 作OM⊥AB于M,过B 作BN⊥CD 于N,则∠CBD=90°.∵∠A= 90°+ ∠ABC, ∴∠A= ∠ABD.∴∠ABD+∠D=∠A+∠D=180°.∴CD∥AB.∴OM=BN,∠DCB=∠ABC.∴AC=BD.∴BD= AC=5.在 Rt△CBD 中,CD= 即点 O到AB 的距离为 .
13.解:(1)如图①,∠DAC 为所作.(答案不唯一)(5分)
(2)如图②,∠CBD 为所作.(10分)
14.(1)证明:如图,作OH⊥CD 于H,∴CH = DH,AH = BH.
∴AH+ DH = BH + CH. A
∴AD=BC.(6分)
(2)解:如图,连接OC.设CH=x,在Rt△OCH中, 在 Rt△OAH中,( 解得 .(12分)
15.(1)证明:连接OC.∵D 为 的中点, ∴∠A=∠DOB.(6分)
(2)解:DE 与⊙O 相切.理由如下:∵∠A=∠DOB,∴AE∥OD.∵DE⊥AE,∴OD⊥DE.∴DE 与⊙O 相切.(12分)
16.(1)证明:连接OD.∵PA 切⊙O 于 A,∴PA⊥AB,即∠PAO=90°.∵OP ∥BD,∴∠DBO=∠AOP,∠BDO = ∠DOP. ∵ OD = OB,∴∠BDO=∠DBO.∴∠DOP = ∠AOP.在△AOP 和△DOP 中 ∴△AOP ≌△DOP (SAS). ∴∠PDO =∠PAO=90°,即OD⊥PD.∵OD 是⊙O 的半径,∴PD 是⊙O 的切线.(7分)
(2)解:由(1)知△AOP≌△DOP,∴PA=PD.
∵四边形 POBD 是平行四边形,∴PD=OB.
∵OB=OA,∴PA=OA.∴∠APO=∠AOP.
∵∠PAO= 90°, ∴ ∠APO = ∠AOP = 45°.(14分)
同课章节目录
