24.4 弧长和扇形面积第 1 课时 弧长和扇形面积 同步练习(含答案)2024—2025学年人教版数学九年级上册
文档属性
| 名称 | 24.4 弧长和扇形面积第 1 课时 弧长和扇形面积 同步练习(含答案)2024—2025学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 508.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-03 06:00:41 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
24.4 弧长和扇形面积
第 1 课时 弧长和扇形面积
A层
知识点一 与弧长有关的计算
1.若扇形的半径为3,圆心角为 60°,则此扇形的弧长是 ( )
A. π B.π C. π D.2π
【变式题】由公式求弧长→已知弧长求圆心角或圆的半径
(1)一个扇形的弧长是11πcm,半径是18cm,则此扇形的圆心角是 .
(2)一个扇形的弧长是8πcm,圆心角是 144°,则此扇形的半径是 cm.
2.如图,在扇形 OAB 中,AC 为弦,∠AOB =130°,∠CAO =60°,OA =6,则. 的长为
3.如图所示的扇形中,已知OA=20,AC=30,AB=40,则
4.如图,. 的半径OA=2,OC⊥AB 于点C,∠AOC=60°.
(1)求弦 AB 的长;
(2)求. 的长.
知识点二 与扇形面积有关的计算
5.已知扇形的半径为6,圆心角为 150°,则它的面积是 ( )
A. π B.3π C.5π D.15π
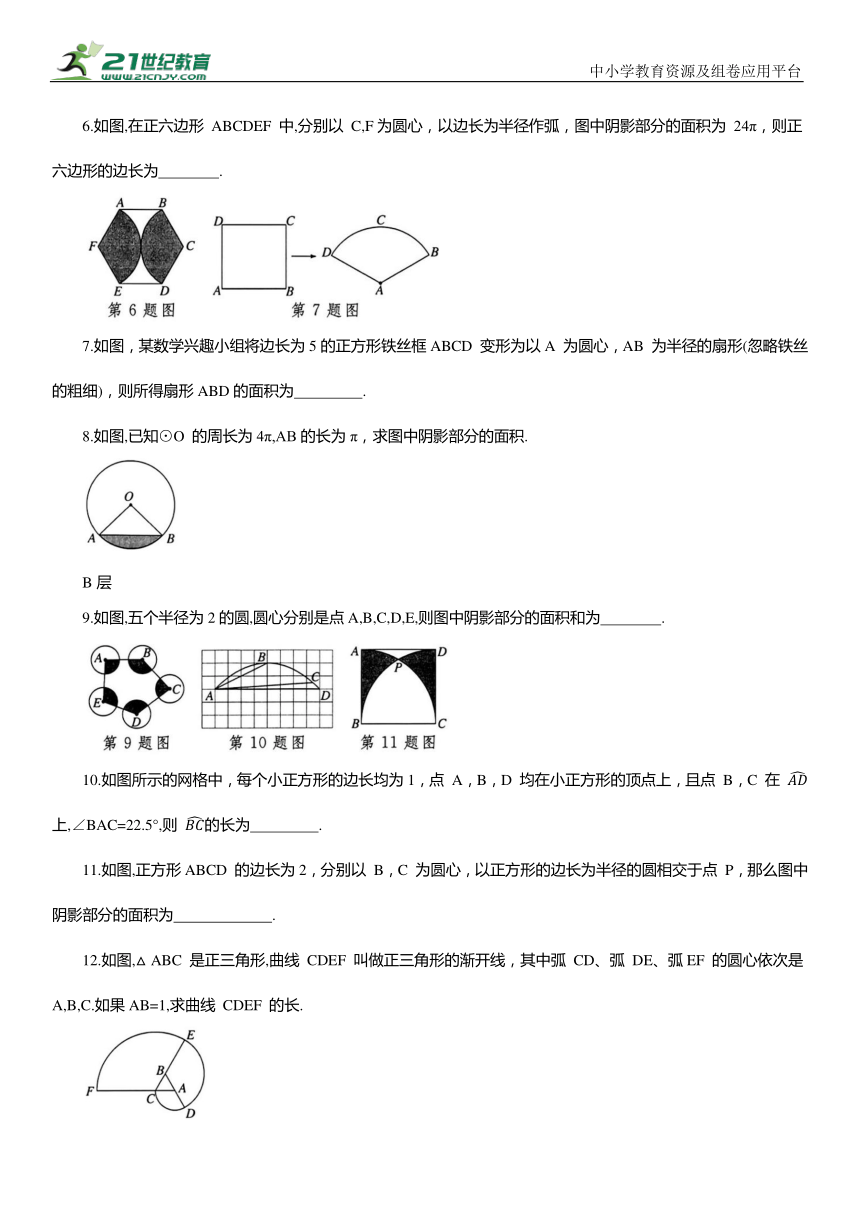
6.如图,在正六边形 ABCDEF 中,分别以 C,F为圆心,以边长为半径作弧,图中阴影部分的面积为 24π,则正六边形的边长为 .
7.如图,某数学兴趣小组将边长为5的正方形铁丝框ABCD 变形为以A 为圆心,AB 为半径的扇形(忽略铁丝的粗细),则所得扇形ABD的面积为 .
8.如图,已知⊙O 的周长为4π,AB的长为π,求图中阴影部分的面积.
B层
9.如图,五个半径为2的圆,圆心分别是点A,B,C,D,E,则图中阴影部分的面积和为 .
10.如图所示的网格中,每个小正方形的边长均为1,点 A,B,D 均在小正方形的顶点上,且点 B,C 在 上,∠BAC=22.5°,则 的长为 .
11.如图,正方形ABCD 的边长为2,分别以 B,C 为圆心,以正方形的边长为半径的圆相交于点 P,那么图中阴影部分的面积为 .
12.如图,△ABC 是正三角形,曲线 CDEF 叫做正三角形的渐开线,其中弧 CD、弧 DE、弧EF 的圆心依次是A,B,C.如果AB=1,求曲线 CDEF 的长.
13.如图,在⊙O 中,半径OA⊥OB,过OA 的中点C 作 FD∥OB 交⊙O 于 D,F 两点,且CD= ,以 O 为圆心,OC 为半径作( ,交 OB 于E 点.
(1)求⊙O 的半径;
(2)计算阴影部分的面积.
C层
14.如图,CD 是⊙O 的直径,AB 是⊙O 的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.
(1)求⊙O 的半径;
(2)点 E 为圆上一点,∠ECD=15°,将 沿弦CE 翻折,交CD 于点F,求图中阴影部分的面积.
第 1课时 弧长和扇形面积
1. B 【变式题】(1)110° (2)10 2.π/3 3.1004.解:(1)∵AB的半径 OA =2,OC⊥AB,∠AOC= 60°, ∴ AB = 2AC, ∠OAC = 30°.
(2)∵OA =OB,∴∠OAB =∠OBA =30°.
的长是
5. D 6.6 7.25
8.解:∵⊙O的周长为4π,∴⊙O 的半径是r= 的长为π, 的长等于⊙O的周长的 2×2÷2=π-2.
解析:如图,连接PB、PC,作 PF⊥BC 于 F.∵PB=PC=BC,∴△PBC 为等边三角形.∴∠PBC = 60°,∠PBA = 30°. 易 得 则
12.解:∵△ABC 是正三角形,∴AB = BC =CA=1,∠ABC=∠BCA=∠CAB=60°.∴∠CAD=∠DBE=∠FCE=120°.∴曲线 CDEF 的 长 为
13.解:(1)连接 OD.∵OA⊥OB,∴∠AOB=90°.∵CD∥OB,∴∠OCD=90°.∵C是AO中点,∴OD = 2CO.设OC=x,∴x + 或x=--1(舍去).∴OD=2.∴⊙O的半径为2.
(2)连接AD,则易得 AD=OD,∴△AOD 为等边三角形.∴∠AOD=60°.∴∠DOB=30°.
14.解:(1)连接AO,如图①所示.∵CD 为⊙O的直径,,AB⊥CD,AB=8,∴AG= AB=4.∵OG : OC=3:5,∴设⊙O的半径为5k,则 解得k=1,或k=-1(舍去).∴5k=5,即⊙O的半径是5.
(2)如图②所示,将阴影部分沿CE 翻折,点 F的对应点为M,则 15°,∴由对称性可知∠DCM=30°.连接OM,则∠MOD=60°,∴∠MOC=120°.过点 M 作MN⊥CD 于点 N,∴∠NMO=30°.∴ON=
24.4 弧长和扇形面积
第 1 课时 弧长和扇形面积
A层
知识点一 与弧长有关的计算
1.若扇形的半径为3,圆心角为 60°,则此扇形的弧长是 ( )
A. π B.π C. π D.2π
【变式题】由公式求弧长→已知弧长求圆心角或圆的半径
(1)一个扇形的弧长是11πcm,半径是18cm,则此扇形的圆心角是 .
(2)一个扇形的弧长是8πcm,圆心角是 144°,则此扇形的半径是 cm.
2.如图,在扇形 OAB 中,AC 为弦,∠AOB =130°,∠CAO =60°,OA =6,则. 的长为
3.如图所示的扇形中,已知OA=20,AC=30,AB=40,则
4.如图,. 的半径OA=2,OC⊥AB 于点C,∠AOC=60°.
(1)求弦 AB 的长;
(2)求. 的长.
知识点二 与扇形面积有关的计算
5.已知扇形的半径为6,圆心角为 150°,则它的面积是 ( )
A. π B.3π C.5π D.15π
6.如图,在正六边形 ABCDEF 中,分别以 C,F为圆心,以边长为半径作弧,图中阴影部分的面积为 24π,则正六边形的边长为 .
7.如图,某数学兴趣小组将边长为5的正方形铁丝框ABCD 变形为以A 为圆心,AB 为半径的扇形(忽略铁丝的粗细),则所得扇形ABD的面积为 .
8.如图,已知⊙O 的周长为4π,AB的长为π,求图中阴影部分的面积.
B层
9.如图,五个半径为2的圆,圆心分别是点A,B,C,D,E,则图中阴影部分的面积和为 .
10.如图所示的网格中,每个小正方形的边长均为1,点 A,B,D 均在小正方形的顶点上,且点 B,C 在 上,∠BAC=22.5°,则 的长为 .
11.如图,正方形ABCD 的边长为2,分别以 B,C 为圆心,以正方形的边长为半径的圆相交于点 P,那么图中阴影部分的面积为 .
12.如图,△ABC 是正三角形,曲线 CDEF 叫做正三角形的渐开线,其中弧 CD、弧 DE、弧EF 的圆心依次是A,B,C.如果AB=1,求曲线 CDEF 的长.
13.如图,在⊙O 中,半径OA⊥OB,过OA 的中点C 作 FD∥OB 交⊙O 于 D,F 两点,且CD= ,以 O 为圆心,OC 为半径作( ,交 OB 于E 点.
(1)求⊙O 的半径;
(2)计算阴影部分的面积.
C层
14.如图,CD 是⊙O 的直径,AB 是⊙O 的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.
(1)求⊙O 的半径;
(2)点 E 为圆上一点,∠ECD=15°,将 沿弦CE 翻折,交CD 于点F,求图中阴影部分的面积.
第 1课时 弧长和扇形面积
1. B 【变式题】(1)110° (2)10 2.π/3 3.1004.解:(1)∵AB的半径 OA =2,OC⊥AB,∠AOC= 60°, ∴ AB = 2AC, ∠OAC = 30°.
(2)∵OA =OB,∴∠OAB =∠OBA =30°.
的长是
5. D 6.6 7.25
8.解:∵⊙O的周长为4π,∴⊙O 的半径是r= 的长为π, 的长等于⊙O的周长的 2×2÷2=π-2.
解析:如图,连接PB、PC,作 PF⊥BC 于 F.∵PB=PC=BC,∴△PBC 为等边三角形.∴∠PBC = 60°,∠PBA = 30°. 易 得 则
12.解:∵△ABC 是正三角形,∴AB = BC =CA=1,∠ABC=∠BCA=∠CAB=60°.∴∠CAD=∠DBE=∠FCE=120°.∴曲线 CDEF 的 长 为
13.解:(1)连接 OD.∵OA⊥OB,∴∠AOB=90°.∵CD∥OB,∴∠OCD=90°.∵C是AO中点,∴OD = 2CO.设OC=x,∴x + 或x=--1(舍去).∴OD=2.∴⊙O的半径为2.
(2)连接AD,则易得 AD=OD,∴△AOD 为等边三角形.∴∠AOD=60°.∴∠DOB=30°.
14.解:(1)连接AO,如图①所示.∵CD 为⊙O的直径,,AB⊥CD,AB=8,∴AG= AB=4.∵OG : OC=3:5,∴设⊙O的半径为5k,则 解得k=1,或k=-1(舍去).∴5k=5,即⊙O的半径是5.
(2)如图②所示,将阴影部分沿CE 翻折,点 F的对应点为M,则 15°,∴由对称性可知∠DCM=30°.连接OM,则∠MOD=60°,∴∠MOC=120°.过点 M 作MN⊥CD 于点 N,∴∠NMO=30°.∴ON=
同课章节目录
