解题技巧专题:圆中的最值问题(含隐圆问题)同步练习(含答案) 2024—2025学年人教版数学九年级上册
文档属性
| 名称 | 解题技巧专题:圆中的最值问题(含隐圆问题)同步练习(含答案) 2024—2025学年人教版数学九年级上册 | 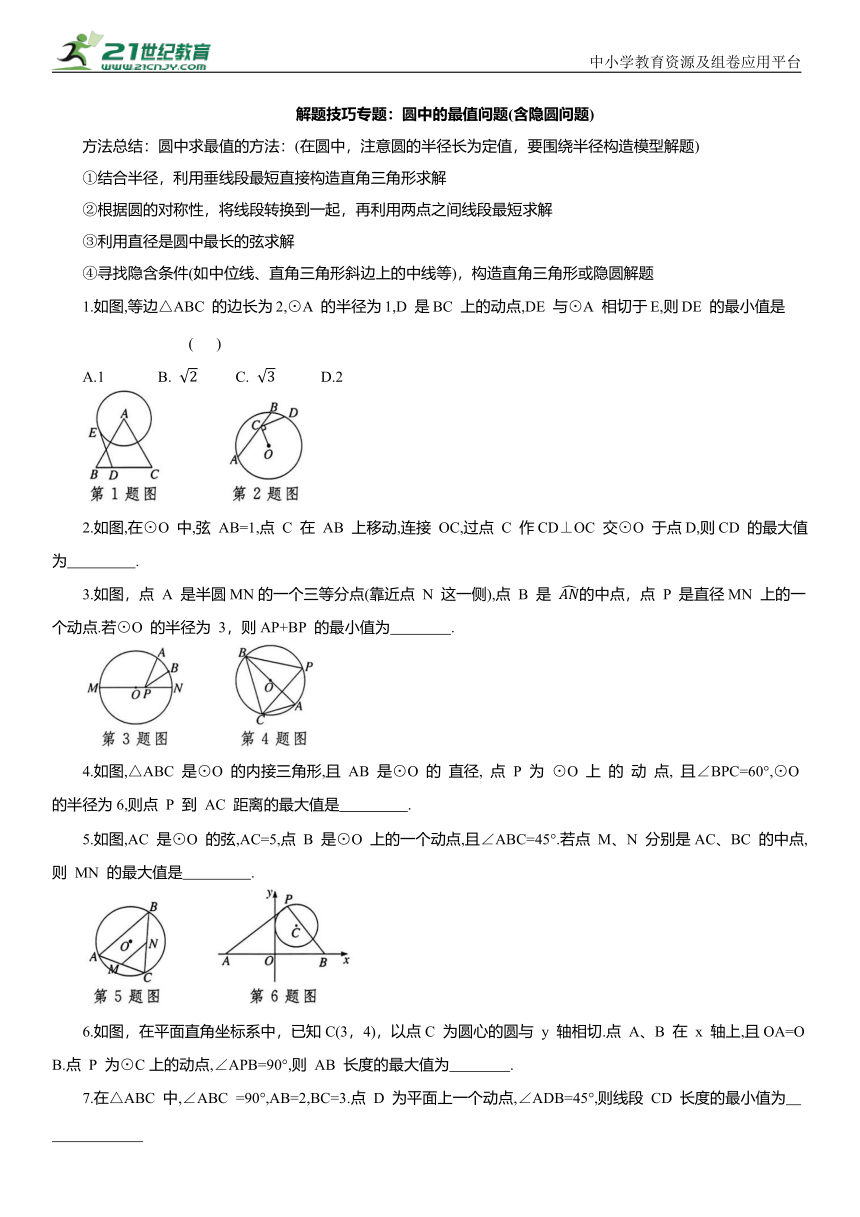 | |
| 格式 | docx | ||
| 文件大小 | 276.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-03 05:47:47 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
解题技巧专题:圆中的最值问题(含隐圆问题)
方法总结:圆中求最值的方法:(在圆中,注意圆的半径长为定值,要围绕半径构造模型解题)
①结合半径,利用垂线段最短直接构造直角三角形求解
②根据圆的对称性,将线段转换到一起,再利用两点之间线段最短求解
③利用直径是圆中最长的弦求解
④寻找隐含条件(如中位线、直角三角形斜边上的中线等),构造直角三角形或隐圆解题
1.如图,等边△ABC 的边长为2,⊙A 的半径为1,D 是BC 上的动点,DE 与⊙A 相切于E,则DE 的最小值是 ( )
A.1 B. C. D.2
2.如图,在⊙O 中,弦 AB=1,点 C 在 AB 上移动,连接 OC,过点 C 作CD⊥OC 交⊙O 于点D,则CD 的最大值为 .
3.如图,点 A 是半圆MN的一个三等分点(靠近点 N 这一侧),点 B 是 的中点,点 P 是直径MN 上的一个动点.若⊙O 的半径为 3,则AP+BP 的最小值为 .
4.如图,△ABC 是⊙O 的内接三角形,且 AB 是⊙O 的 直径, 点 P 为 ⊙O 上 的 动 点, 且∠BPC=60°,⊙O 的半径为6,则点 P 到 AC 距离的最大值是 .
5.如图,AC 是⊙O 的弦,AC=5,点 B 是⊙O 上的一个动点,且∠ABC=45°.若点 M、N 分别是AC、BC 的中点,则 MN 的最大值是 .
6.如图,在平面直角坐标系中,已知C(3,4),以点C 为圆心的圆与 y 轴相切.点 A、B 在 x 轴上,且OA=OB.点 P 为⊙C上的动点,∠APB=90°,则 AB 长度的最大值为 .
7.在△ABC 中,∠ABC =90°,AB=2,BC=3.点 D 为平面上一个动点,∠ADB=45°,则线段 CD 长度的最小值为
8.如图,AB 是⊙O 的直径,点 C、D 是⊙O 上的点,且 OD∥BC,AC 分别与 BD、OD 相交于点 E、F.
(1)求证:点 D 为. 的中点;
(2)若CB=6,AB=10,求 DF 的长;
(3)若⊙O 的半径为5,∠DOA=80°,点 P 是线段AB 上任意一点,试求出 PC+PD 的最小值.
解题技巧专题:圆中的最值问题(含隐圆问题)
1. B 2. 3.3 4.6+3.
6.16
解析:如图,作△ABD的外接圆O(因求 CD 最小值,故圆心 O在AB 的右侧),连接OC,当O、D、C 三 点 共 线 时,CD 的 值 最 小.∵∠ADB=45°,∴∠AOB=90°.∴△AOB 为等腰直角三角形. ∵∠OBA=45°,∠ABC=90°,∴∠OBC=45°.作OE⊥BC 于点E,∴△OBE 为等腰直角三角形 3-1=2.在 Rt△OEC 中, 当O、D、C 三点共线时,CD 最小为
8.(1)证明:∵AB 是⊙O 的直径,∴∠ACB=90°.∵OD ∥BC,∴∠OFA =90°.∴OF⊥ 即点 D 为 的中点.
(2)解:∵OF⊥AC,∴AF=CF.而OA=OB,∴OF为△ACB 的中位线. ∵AB=10,∴OD=5.∴DF=OD-OF=5-3=2.
(3)解:作C 点关于AB 的对称点 C',连接C'D交 AB 于 P,连接 OC, 如 图.∵PC= PC', .此时 PC+PD 的 值 最 小.∵AD =CD,∴∠COD =∠AOD=80°.∴∠BOC=20°.∵点 C 和点 C'关于AB 对称,∴∠C'OB=20°.∴∠DOC'=120°. .作 OH⊥DC'于 H,则 .在 Rt△OHD 中, 5 .∴PC+PD的最小值为 5 .
解题技巧专题:圆中的最值问题(含隐圆问题)
方法总结:圆中求最值的方法:(在圆中,注意圆的半径长为定值,要围绕半径构造模型解题)
①结合半径,利用垂线段最短直接构造直角三角形求解
②根据圆的对称性,将线段转换到一起,再利用两点之间线段最短求解
③利用直径是圆中最长的弦求解
④寻找隐含条件(如中位线、直角三角形斜边上的中线等),构造直角三角形或隐圆解题
1.如图,等边△ABC 的边长为2,⊙A 的半径为1,D 是BC 上的动点,DE 与⊙A 相切于E,则DE 的最小值是 ( )
A.1 B. C. D.2
2.如图,在⊙O 中,弦 AB=1,点 C 在 AB 上移动,连接 OC,过点 C 作CD⊥OC 交⊙O 于点D,则CD 的最大值为 .
3.如图,点 A 是半圆MN的一个三等分点(靠近点 N 这一侧),点 B 是 的中点,点 P 是直径MN 上的一个动点.若⊙O 的半径为 3,则AP+BP 的最小值为 .
4.如图,△ABC 是⊙O 的内接三角形,且 AB 是⊙O 的 直径, 点 P 为 ⊙O 上 的 动 点, 且∠BPC=60°,⊙O 的半径为6,则点 P 到 AC 距离的最大值是 .
5.如图,AC 是⊙O 的弦,AC=5,点 B 是⊙O 上的一个动点,且∠ABC=45°.若点 M、N 分别是AC、BC 的中点,则 MN 的最大值是 .
6.如图,在平面直角坐标系中,已知C(3,4),以点C 为圆心的圆与 y 轴相切.点 A、B 在 x 轴上,且OA=OB.点 P 为⊙C上的动点,∠APB=90°,则 AB 长度的最大值为 .
7.在△ABC 中,∠ABC =90°,AB=2,BC=3.点 D 为平面上一个动点,∠ADB=45°,则线段 CD 长度的最小值为
8.如图,AB 是⊙O 的直径,点 C、D 是⊙O 上的点,且 OD∥BC,AC 分别与 BD、OD 相交于点 E、F.
(1)求证:点 D 为. 的中点;
(2)若CB=6,AB=10,求 DF 的长;
(3)若⊙O 的半径为5,∠DOA=80°,点 P 是线段AB 上任意一点,试求出 PC+PD 的最小值.
解题技巧专题:圆中的最值问题(含隐圆问题)
1. B 2. 3.3 4.6+3.
6.16
解析:如图,作△ABD的外接圆O(因求 CD 最小值,故圆心 O在AB 的右侧),连接OC,当O、D、C 三 点 共 线 时,CD 的 值 最 小.∵∠ADB=45°,∴∠AOB=90°.∴△AOB 为等腰直角三角形. ∵∠OBA=45°,∠ABC=90°,∴∠OBC=45°.作OE⊥BC 于点E,∴△OBE 为等腰直角三角形 3-1=2.在 Rt△OEC 中, 当O、D、C 三点共线时,CD 最小为
8.(1)证明:∵AB 是⊙O 的直径,∴∠ACB=90°.∵OD ∥BC,∴∠OFA =90°.∴OF⊥ 即点 D 为 的中点.
(2)解:∵OF⊥AC,∴AF=CF.而OA=OB,∴OF为△ACB 的中位线. ∵AB=10,∴OD=5.∴DF=OD-OF=5-3=2.
(3)解:作C 点关于AB 的对称点 C',连接C'D交 AB 于 P,连接 OC, 如 图.∵PC= PC', .此时 PC+PD 的 值 最 小.∵AD =CD,∴∠COD =∠AOD=80°.∴∠BOC=20°.∵点 C 和点 C'关于AB 对称,∴∠C'OB=20°.∴∠DOC'=120°. .作 OH⊥DC'于 H,则 .在 Rt△OHD 中, 5 .∴PC+PD的最小值为 5 .
同课章节目录
