24.2.2 直线和圆的位置关系第 2 课时 切线的判定与性质 同步练习(含答案)
文档属性
| 名称 | 24.2.2 直线和圆的位置关系第 2 课时 切线的判定与性质 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 433.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-03 06:09:19 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
24.2.2 直线和圆的位置关系
第 2 课时 切线的判定与性质
A层
知识点一 切线的判定
1.下列说法中,不正确的是 ( )
A.与圆只有一个交点的直线是圆的切线
B.经过半径的外端,且垂直于这条半径的直线是圆的切线
C.与圆心的距离等于这个圆的半径的直线是圆的切线
D.垂直于半径的直线是圆的切线
2.如图,A 是⊙O 上一点,且AO=5,PO=13,AP=12,则 PA 与⊙O 的位置关系是 .
3.如图,AB 是⊙O 的直径,点 C 为⊙O 上一点,过点 B 作BD⊥CD,垂足为 D,连接 BC,BC平分∠ABD.求证:CD 为⊙O 的切线.
知识点二 切线的性质
4.如图,AB 是⊙O 的直径,BC 是⊙O 的切线.若∠BAC=35°,则∠ACB的大小为 ( )
A.35° B.45° C.55° D.65°
5.如图,已知⊙O 的半径为1,点 P 是⊙O 外一点,且 OP =2.若 PT 是⊙O 的切线,T 为切点,连接 OT,则 PT =
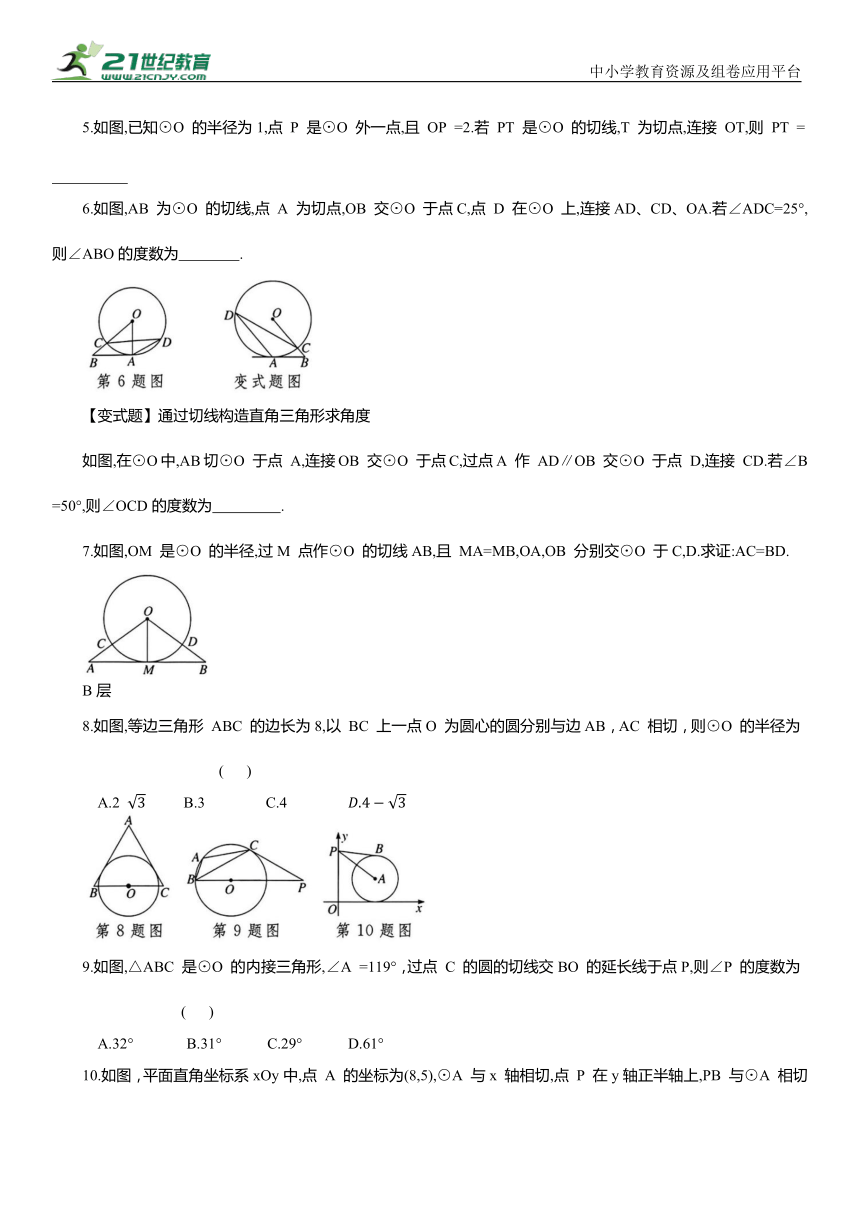
6.如图,AB 为⊙O 的切线,点 A 为切点,OB 交⊙O 于点C,点 D 在⊙O 上,连接AD、CD、OA.若∠ADC=25°,则∠ABO的度数为 .
【变式题】通过切线构造直角三角形求角度
如图,在⊙O中,AB切⊙O 于点 A,连接OB 交⊙O 于点C,过点A 作 AD∥OB 交⊙O 于点 D,连接 CD.若∠B=50°,则∠OCD的度数为 .
7.如图,OM 是⊙O 的半径,过M 点作⊙O 的切线AB,且 MA=MB,OA,OB 分别交⊙O 于C,D.求证:AC=BD.
B层
8.如图,等边三角形 ABC 的边长为8,以 BC 上一点O 为圆心的圆分别与边AB,AC 相切,则⊙O 的半径为 ( )
A.2 B.3 C.4
9.如图,△ABC 是⊙O 的内接三角形,∠A =119°,过点 C 的圆的切线交BO 的延长线于点P,则∠P 的度数为 ( )
A.32° B.31° C.29° D.61°
10.如图,平面直角坐标系xOy中,点 A 的坐标为(8,5),⊙A 与x 轴相切,点 P 在y轴正半轴上,PB 与⊙A 相切于点 B.若∠APB=30°,则点 P 的坐标为
11.如图,△ABC 是⊙O 的内接三角形,AC 是⊙O 的直径,点 D 是 的中点,DE∥BC 交AC 的延长线于点E.
(1)求证:直线 DE 与⊙O 相切;
(2)若⊙O 的直径是10,∠A=45°,求 CE 的长.
12.如图,在 Rt△ABC 中,∠C=90°,点 O 在AC上,以OA 为半径的半圆O交AB 于点D,交AC 于点E,过点 D 作半圆O 的切线DF,交BC 于点 F.
(1)求证:BF=DF;
(2)若 AC=4,BC=3,CF=1,求半圆O 的半径长.
C层
13.如图,AB 为⊙O 的直径,C 为⊙O 上一点,CD⊥AB 于点 D,P 为AB 延长线上一点,∠PCD=2∠BAC.
(1)求证:CP 为⊙O 的切线;
(2)若BP=1,CP= .
①求⊙O 的半径;
②若M为 AC 上一动点,求 OM+DM 的最小值.
第 2 课时 切线的判定与性质
1. D 2.相切
3.证明:∵BC平分∠ABD,∴∠OBC=∠DBC.∵OB=OC,∴∠OBC=∠OCB.∴∠OCB=∠DBC.∴OC∥BD.∵BD⊥CD,∴OC⊥CD.∵OC 为半径,∴CD 为⊙O的切线.
4. C 5. 6.40° 【变式题】20°
7.证明:由题意知,AB 切⊙O 于点 M,∴OM⊥AB.又∵MA=MB,∴OA=OB.∵OC=OD,∴OA-OC=OB-OD,即AC=BD.
8. A 9. A 10.(0,11)
11.(1)证明:如图,连接OD.∵点 D 是 的中点,∴OD⊥ BC. ∵ DE ∥BC,∴OD⊥DE.∴直线DE 与⊙O 相切.
(2)解:∵AC 是⊙O 的直径,∴∠B=90°.∵∠A=45°,∴∠ACB =45°.∵BC ∥DE,∴∠E=45°.而∠ODE=90°,∴△ODE 为等腰直角 三 角形.∴OD = DE.∴ 易得 OE =
12.(1)证明:如图,连接 OD.∵DF 是半 圆 O 的切线,∴∠ODF=90°.∴∠ADO+∠BDF= 90°.∵ OA = OD, ∴ ∠OAD =∠ODA.∴∠OAD+∠BDF =90°.∵∠C =90°,∴∠OAD+∠B=90°.∴∠B=∠BDF.∴BF=DF.
(2)解:如图,连接OF.设半圆O的半径为r,则OD=OA=r.∵AC=4,BC=3,CF=1,
∴OC=4-r,DF=BF=3--1=2.∵OD + 故半圆O的半径为 .
13.(1) 证明:如图,连 接 OC.∵OA= OC, ∴∠CAO =∠ACO.∴∠POC = 2∠BAC.
∵∠PCD = 2∠BAC, ∴∠POC = ∠PCD.
∵CD⊥ AB 于 点 D, ∴∠ODC = 90°.
∴∠POC+∠OCD=90°.∴∠PCD+∠OCD=90°.∴∠OCP=90°.∴半径 OC⊥CP.∴CP为⊙O 的切线.
(2)解:①设⊙O 的半径为r.在 Rt△OCP中, 解得 r=2.∴⊙O的半径为2.
②如图,作点 O 关于 AC 的对称点 E,连接AE,EC,ED,ED 交AC 于点 M,连接OM,此时OM+DM=ED即为所求.∵AC垂直平分OE,∴AE=AO=OC=CE=2.∴四边形AOCE 是菱形.∴EC∥AO.∴∠ECD=90°.∵OB=2,PB = 1,∴OP= 3.∵S△OCP = 在Rt△ECD 中, 的最小值为
24.2.2 直线和圆的位置关系
第 2 课时 切线的判定与性质
A层
知识点一 切线的判定
1.下列说法中,不正确的是 ( )
A.与圆只有一个交点的直线是圆的切线
B.经过半径的外端,且垂直于这条半径的直线是圆的切线
C.与圆心的距离等于这个圆的半径的直线是圆的切线
D.垂直于半径的直线是圆的切线
2.如图,A 是⊙O 上一点,且AO=5,PO=13,AP=12,则 PA 与⊙O 的位置关系是 .
3.如图,AB 是⊙O 的直径,点 C 为⊙O 上一点,过点 B 作BD⊥CD,垂足为 D,连接 BC,BC平分∠ABD.求证:CD 为⊙O 的切线.
知识点二 切线的性质
4.如图,AB 是⊙O 的直径,BC 是⊙O 的切线.若∠BAC=35°,则∠ACB的大小为 ( )
A.35° B.45° C.55° D.65°
5.如图,已知⊙O 的半径为1,点 P 是⊙O 外一点,且 OP =2.若 PT 是⊙O 的切线,T 为切点,连接 OT,则 PT =
6.如图,AB 为⊙O 的切线,点 A 为切点,OB 交⊙O 于点C,点 D 在⊙O 上,连接AD、CD、OA.若∠ADC=25°,则∠ABO的度数为 .
【变式题】通过切线构造直角三角形求角度
如图,在⊙O中,AB切⊙O 于点 A,连接OB 交⊙O 于点C,过点A 作 AD∥OB 交⊙O 于点 D,连接 CD.若∠B=50°,则∠OCD的度数为 .
7.如图,OM 是⊙O 的半径,过M 点作⊙O 的切线AB,且 MA=MB,OA,OB 分别交⊙O 于C,D.求证:AC=BD.
B层
8.如图,等边三角形 ABC 的边长为8,以 BC 上一点O 为圆心的圆分别与边AB,AC 相切,则⊙O 的半径为 ( )
A.2 B.3 C.4
9.如图,△ABC 是⊙O 的内接三角形,∠A =119°,过点 C 的圆的切线交BO 的延长线于点P,则∠P 的度数为 ( )
A.32° B.31° C.29° D.61°
10.如图,平面直角坐标系xOy中,点 A 的坐标为(8,5),⊙A 与x 轴相切,点 P 在y轴正半轴上,PB 与⊙A 相切于点 B.若∠APB=30°,则点 P 的坐标为
11.如图,△ABC 是⊙O 的内接三角形,AC 是⊙O 的直径,点 D 是 的中点,DE∥BC 交AC 的延长线于点E.
(1)求证:直线 DE 与⊙O 相切;
(2)若⊙O 的直径是10,∠A=45°,求 CE 的长.
12.如图,在 Rt△ABC 中,∠C=90°,点 O 在AC上,以OA 为半径的半圆O交AB 于点D,交AC 于点E,过点 D 作半圆O 的切线DF,交BC 于点 F.
(1)求证:BF=DF;
(2)若 AC=4,BC=3,CF=1,求半圆O 的半径长.
C层
13.如图,AB 为⊙O 的直径,C 为⊙O 上一点,CD⊥AB 于点 D,P 为AB 延长线上一点,∠PCD=2∠BAC.
(1)求证:CP 为⊙O 的切线;
(2)若BP=1,CP= .
①求⊙O 的半径;
②若M为 AC 上一动点,求 OM+DM 的最小值.
第 2 课时 切线的判定与性质
1. D 2.相切
3.证明:∵BC平分∠ABD,∴∠OBC=∠DBC.∵OB=OC,∴∠OBC=∠OCB.∴∠OCB=∠DBC.∴OC∥BD.∵BD⊥CD,∴OC⊥CD.∵OC 为半径,∴CD 为⊙O的切线.
4. C 5. 6.40° 【变式题】20°
7.证明:由题意知,AB 切⊙O 于点 M,∴OM⊥AB.又∵MA=MB,∴OA=OB.∵OC=OD,∴OA-OC=OB-OD,即AC=BD.
8. A 9. A 10.(0,11)
11.(1)证明:如图,连接OD.∵点 D 是 的中点,∴OD⊥ BC. ∵ DE ∥BC,∴OD⊥DE.∴直线DE 与⊙O 相切.
(2)解:∵AC 是⊙O 的直径,∴∠B=90°.∵∠A=45°,∴∠ACB =45°.∵BC ∥DE,∴∠E=45°.而∠ODE=90°,∴△ODE 为等腰直角 三 角形.∴OD = DE.∴ 易得 OE =
12.(1)证明:如图,连接 OD.∵DF 是半 圆 O 的切线,∴∠ODF=90°.∴∠ADO+∠BDF= 90°.∵ OA = OD, ∴ ∠OAD =∠ODA.∴∠OAD+∠BDF =90°.∵∠C =90°,∴∠OAD+∠B=90°.∴∠B=∠BDF.∴BF=DF.
(2)解:如图,连接OF.设半圆O的半径为r,则OD=OA=r.∵AC=4,BC=3,CF=1,
∴OC=4-r,DF=BF=3--1=2.∵OD + 故半圆O的半径为 .
13.(1) 证明:如图,连 接 OC.∵OA= OC, ∴∠CAO =∠ACO.∴∠POC = 2∠BAC.
∵∠PCD = 2∠BAC, ∴∠POC = ∠PCD.
∵CD⊥ AB 于 点 D, ∴∠ODC = 90°.
∴∠POC+∠OCD=90°.∴∠PCD+∠OCD=90°.∴∠OCP=90°.∴半径 OC⊥CP.∴CP为⊙O 的切线.
(2)解:①设⊙O 的半径为r.在 Rt△OCP中, 解得 r=2.∴⊙O的半径为2.
②如图,作点 O 关于 AC 的对称点 E,连接AE,EC,ED,ED 交AC 于点 M,连接OM,此时OM+DM=ED即为所求.∵AC垂直平分OE,∴AE=AO=OC=CE=2.∴四边形AOCE 是菱形.∴EC∥AO.∴∠ECD=90°.∵OB=2,PB = 1,∴OP= 3.∵S△OCP = 在Rt△ECD 中, 的最小值为
同课章节目录
