23.2 中心对称 同步练习 (含答案)2024—2025学年人教版数学九年级上册
文档属性
| 名称 | 23.2 中心对称 同步练习 (含答案)2024—2025学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 885.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-03 00:00:00 | ||
图片预览


文档简介
23.2 中心对称
23.2.1 中心对称
A层
知识点一 认识中心对称及中心对称的性质
1.下列说法正确的是 ( )
A.全等的两个图形成中心对称
B.成中心对称的两个图形全等
C.成中心对称的两个图形必须重合
D.旋转后能够重合的两个图形成中心对称
2.下列四组图形中,左边的图形与右边的图形不成中心对称的有 ( )
A.1组 B.2 组 C.3组 D.4 组
3.如图,△ABC 与△A'B'C'关于点O 成中心对称,则下列结论不成立的是 ( )
A.点A与点 A'是对称点 B. BO=B'O
C. AB∥A'B' D.∠ACB=∠C'A'B'
4.如图,若四边形 ABCD 与四边形 CEFG 成中心对称,则它们的对称中心是 ,点 A 的对称点是 ,点 E 的对称点是 .BD∥ 且BD= .连接A,F的线段经过点 ,且被点 C ,△ABD≌ .
知识点二 利用中心对称的性质作图
5.如图,在方格网中,已知格点△ABC 和点 O,画出与△ABC关于点 O 成中心对称的△A'B'C'.
B层
6.如图所示的图形是由三个半圆组成的,点O是大半圆的圆心,且AC=CD=BD,与此图形关于点 O 成中心对称的图形是 ( )
7.如图,边长为 2 的正方形ABCD 的对角线相交于点O,过点 O 的直线分别交边AD,BC 于E,F 两点,则阴影部分的面积是 ( )
A.1 B.2 C.3 D.4
【变式题】图变本质不变:利用中心对称的性质将阴影部分移到一起组成规则图形求解
如图,直线a、b垂直相交于点O,曲线C 关于点O成中心对称,点 A 的对称点是点 A',AB⊥a于点 B,A'D⊥b于点 D.若OB=3,OD=2,则阴影部分的面积之和为 .
8.如图,AD 是△ABC 的边 BC上的中线.
(1)画出以点 D 为对称中心且与△ABD 成中心对称的三角形;
(2)若AB=5,AC=7,求 AD 的长l 的取值范围.
中小学教育资源及组卷应用平台
23.2.2 中心对称图形
A层
知识点一 中心对称图形
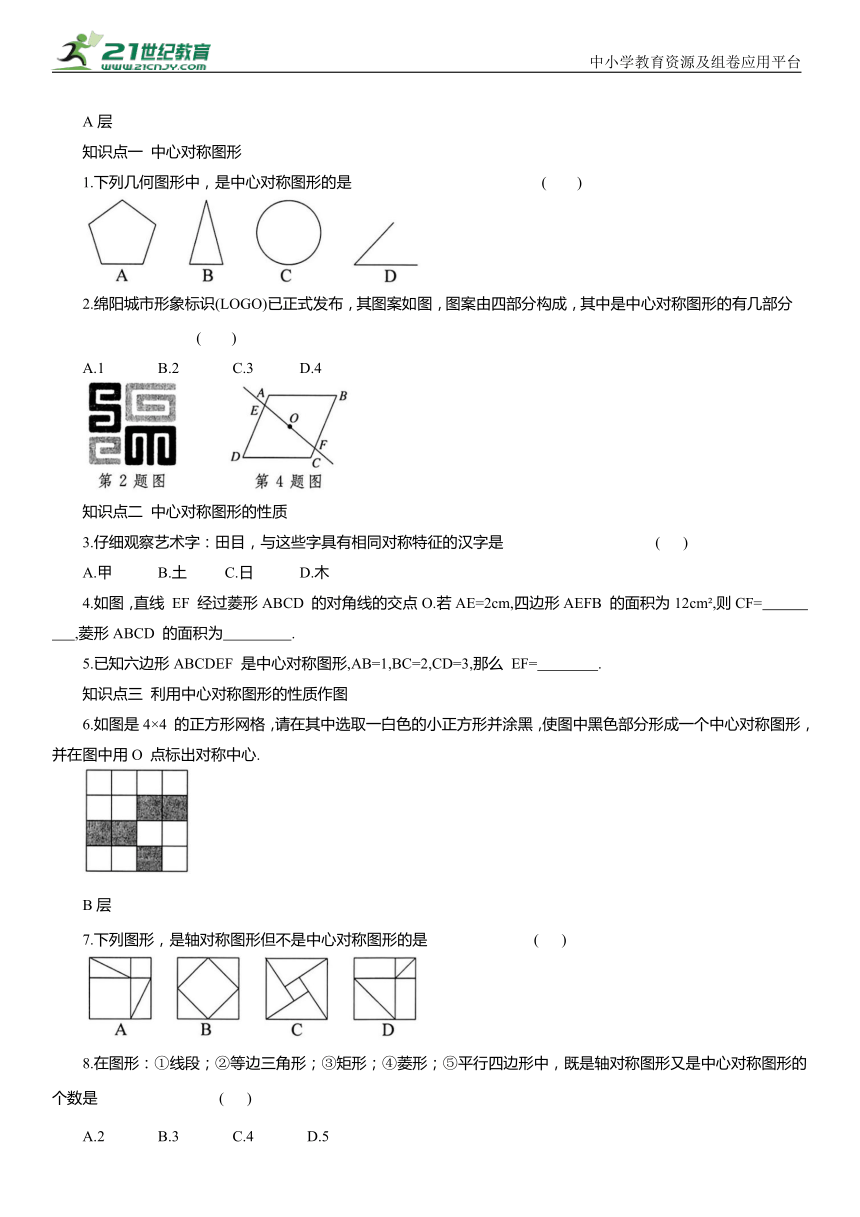
1.下列几何图形中,是中心对称图形的是 ( )
2.绵阳城市形象标识(LOGO)已正式发布,其图案如图,图案由四部分构成,其中是中心对称图形的有几部分 ( )
A.1 B.2 C.3 D.4
知识点二 中心对称图形的性质
3.仔细观察艺术字:田目,与这些字具有相同对称特征的汉字是 ( )
A.甲 B.土 C.日 D.木
4.如图,直线 EF 经过菱形ABCD 的对角线的交点O.若AE=2cm,四边形AEFB 的面积为12cm ,则CF= ,菱形ABCD 的面积为 .
5.已知六边形ABCDEF 是中心对称图形,AB=1,BC=2,CD=3,那么 EF= .
知识点三 利用中心对称图形的性质作图
6.如图是4×4 的正方形网格,请在其中选取一白色的小正方形并涂黑,使图中黑色部分形成一个中心对称图形,并在图中用O 点标出对称中心.
B层
7.下列图形,是轴对称图形但不是中心对称图形的是 ( )
8.在图形:①线段;②等边三角形;③矩形;④菱形;⑤平行四边形中,既是轴对称图形又是中心对称图形的个数是 ( )
A.2 B.3 C.4 D.5
9.如图,在 4×4 的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形既是轴对称图形又是中心对称图形,则这个格点正方形的作法共有 种.
10.阅读材料:对于中心对称图形,过对称中心的任意一条直线都把这个图形分成面积相等的两部分,如图:
尝试应用:将下图空白部分分成面积相等的两部分(不写作法,保留作图痕迹).
23.2.3 关于原点对称的点的坐标
A层
知识点一 求关于原点对称的点的坐标
1.在平面直角坐标系中,点A(3,2)关于原点对称的点的坐标是 ( )
A.(-3,2) B.(3,-2)
C.(-2,-3) D.(-3,-2)
2.在平面直角坐标系中,点 P(-3,m +1).关于原点对称的点在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.在直角坐标系中,将点(--2,3)关于原点的对称点向左平移2个单位长度得到的点的坐标是 .
知识点二 关于原点对称的点的坐标的应用
4.在平面直角坐标系中,点 A(-1,2)和点 B(1,m)关于原点对称,则m 的值为( )
A.2 B.-2 C.-1 D.1
【变式题】在平面直角坐标系中,已知点 A(a,2),B(1,b)关于原点对称,则 的值为( )
A.-1 B.1 C.3 D.5
5.已知点M(2+m,m-1)关于原点的对称点在第二象限,则m 的取值范围是 .
6.如图,每个小正方形的边长为1个单位长度,作出△ABC 关于原点对称的△A B C ,并写出 A 、B 、C 的坐标.
B层
7.如图,把△ABC 绕原点 O 旋转 180°得到△CDA,点 A,B,C的坐标分别为(--5,2),(--2,--2),(5,-2),则点 D 的坐标为( )
A.(2,2) B.(2,—2)
C.(2,5) D.(-2,5)
8.若点 A(a,b)和点 B(m,n)关于原点对称,且a+b=1,则下列结论正确的是( )
A. mn=-1 B. m-n=-1
C. m+n=--1
9.在平面直角坐标系中,若点 P(m,m--n)与点Q(-2,3)关于原点对称,则点 M(m,n)在第 象限.
10.在平面直角坐标系中,已知A(2,3),B(0,1),C(3,1),若线段AC 与 BD 互相平分,则点 D 关于坐标原点的对称点的坐标为 .
11.如图,正方形ABCD 与正方形A B C D 关于某点成中心对称,已知A,D ,D 三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点 B,C,B ,C 的坐标.
23.2 中心对称
23.2.1 中心对称
1. B 2. A 3. D
4.点 C 点 F 点 D GE GE C 平分△FGE
5.解:如图,△A'B'C'即为所求.
6. C 7. A 【变式题】6
8.解:(1)如图,延长 AD 至点A',使 连接CA',则△CDA'即为所求.
(2)根据中心对称的性质可知△ADB≌ 5+7,即2<2AD<12.∴123.2.2 中心对称图形
1. C 2. A 3. C 4.2cm 24cm 5.2
6.解:如图所示,点O 为对称中心.
7. D 8. B 9.4
10.解:如图所示((2)中平分面积的方法不唯一).
23.2.3 关于原点对称的点的坐标1. D 2. D 3.(0,-3)
4. B 【变式题】A 5.-26.解:如图所示,A (2,—2),B (3,0),C (1,1).
7. A 8. C 9.一10.(-5,-3)
11.解:(1)根据对称中心的性质,可得对称中心是 D D 的中点.∵D ,D 的坐标分别是(0,3),(0,2),∴对称中心的坐标是(0,2.5).
(2)∵A,D 的坐标分别是(0,4),(0,2),∴正方形 ABCD 与正方形 A B C D 的边长都是4-2=2.∴B,C的坐标分别是(-2,4),(--2,2).∵A D =2,D 的坐标是(0,3),∴A 的坐标是(0,1).∴B ,C 的坐标分别是(2,1),(2,3).综上所述,可得顶点 B,C,B ,C 的坐标分别是(-2,4),(-2,2),(2,1),(2,3).
23.2.1 中心对称
A层
知识点一 认识中心对称及中心对称的性质
1.下列说法正确的是 ( )
A.全等的两个图形成中心对称
B.成中心对称的两个图形全等
C.成中心对称的两个图形必须重合
D.旋转后能够重合的两个图形成中心对称
2.下列四组图形中,左边的图形与右边的图形不成中心对称的有 ( )
A.1组 B.2 组 C.3组 D.4 组
3.如图,△ABC 与△A'B'C'关于点O 成中心对称,则下列结论不成立的是 ( )
A.点A与点 A'是对称点 B. BO=B'O
C. AB∥A'B' D.∠ACB=∠C'A'B'
4.如图,若四边形 ABCD 与四边形 CEFG 成中心对称,则它们的对称中心是 ,点 A 的对称点是 ,点 E 的对称点是 .BD∥ 且BD= .连接A,F的线段经过点 ,且被点 C ,△ABD≌ .
知识点二 利用中心对称的性质作图
5.如图,在方格网中,已知格点△ABC 和点 O,画出与△ABC关于点 O 成中心对称的△A'B'C'.
B层
6.如图所示的图形是由三个半圆组成的,点O是大半圆的圆心,且AC=CD=BD,与此图形关于点 O 成中心对称的图形是 ( )
7.如图,边长为 2 的正方形ABCD 的对角线相交于点O,过点 O 的直线分别交边AD,BC 于E,F 两点,则阴影部分的面积是 ( )
A.1 B.2 C.3 D.4
【变式题】图变本质不变:利用中心对称的性质将阴影部分移到一起组成规则图形求解
如图,直线a、b垂直相交于点O,曲线C 关于点O成中心对称,点 A 的对称点是点 A',AB⊥a于点 B,A'D⊥b于点 D.若OB=3,OD=2,则阴影部分的面积之和为 .
8.如图,AD 是△ABC 的边 BC上的中线.
(1)画出以点 D 为对称中心且与△ABD 成中心对称的三角形;
(2)若AB=5,AC=7,求 AD 的长l 的取值范围.
中小学教育资源及组卷应用平台
23.2.2 中心对称图形
A层
知识点一 中心对称图形
1.下列几何图形中,是中心对称图形的是 ( )
2.绵阳城市形象标识(LOGO)已正式发布,其图案如图,图案由四部分构成,其中是中心对称图形的有几部分 ( )
A.1 B.2 C.3 D.4
知识点二 中心对称图形的性质
3.仔细观察艺术字:田目,与这些字具有相同对称特征的汉字是 ( )
A.甲 B.土 C.日 D.木
4.如图,直线 EF 经过菱形ABCD 的对角线的交点O.若AE=2cm,四边形AEFB 的面积为12cm ,则CF= ,菱形ABCD 的面积为 .
5.已知六边形ABCDEF 是中心对称图形,AB=1,BC=2,CD=3,那么 EF= .
知识点三 利用中心对称图形的性质作图
6.如图是4×4 的正方形网格,请在其中选取一白色的小正方形并涂黑,使图中黑色部分形成一个中心对称图形,并在图中用O 点标出对称中心.
B层
7.下列图形,是轴对称图形但不是中心对称图形的是 ( )
8.在图形:①线段;②等边三角形;③矩形;④菱形;⑤平行四边形中,既是轴对称图形又是中心对称图形的个数是 ( )
A.2 B.3 C.4 D.5
9.如图,在 4×4 的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形既是轴对称图形又是中心对称图形,则这个格点正方形的作法共有 种.
10.阅读材料:对于中心对称图形,过对称中心的任意一条直线都把这个图形分成面积相等的两部分,如图:
尝试应用:将下图空白部分分成面积相等的两部分(不写作法,保留作图痕迹).
23.2.3 关于原点对称的点的坐标
A层
知识点一 求关于原点对称的点的坐标
1.在平面直角坐标系中,点A(3,2)关于原点对称的点的坐标是 ( )
A.(-3,2) B.(3,-2)
C.(-2,-3) D.(-3,-2)
2.在平面直角坐标系中,点 P(-3,m +1).关于原点对称的点在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.在直角坐标系中,将点(--2,3)关于原点的对称点向左平移2个单位长度得到的点的坐标是 .
知识点二 关于原点对称的点的坐标的应用
4.在平面直角坐标系中,点 A(-1,2)和点 B(1,m)关于原点对称,则m 的值为( )
A.2 B.-2 C.-1 D.1
【变式题】在平面直角坐标系中,已知点 A(a,2),B(1,b)关于原点对称,则 的值为( )
A.-1 B.1 C.3 D.5
5.已知点M(2+m,m-1)关于原点的对称点在第二象限,则m 的取值范围是 .
6.如图,每个小正方形的边长为1个单位长度,作出△ABC 关于原点对称的△A B C ,并写出 A 、B 、C 的坐标.
B层
7.如图,把△ABC 绕原点 O 旋转 180°得到△CDA,点 A,B,C的坐标分别为(--5,2),(--2,--2),(5,-2),则点 D 的坐标为( )
A.(2,2) B.(2,—2)
C.(2,5) D.(-2,5)
8.若点 A(a,b)和点 B(m,n)关于原点对称,且a+b=1,则下列结论正确的是( )
A. mn=-1 B. m-n=-1
C. m+n=--1
9.在平面直角坐标系中,若点 P(m,m--n)与点Q(-2,3)关于原点对称,则点 M(m,n)在第 象限.
10.在平面直角坐标系中,已知A(2,3),B(0,1),C(3,1),若线段AC 与 BD 互相平分,则点 D 关于坐标原点的对称点的坐标为 .
11.如图,正方形ABCD 与正方形A B C D 关于某点成中心对称,已知A,D ,D 三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点 B,C,B ,C 的坐标.
23.2 中心对称
23.2.1 中心对称
1. B 2. A 3. D
4.点 C 点 F 点 D GE GE C 平分△FGE
5.解:如图,△A'B'C'即为所求.
6. C 7. A 【变式题】6
8.解:(1)如图,延长 AD 至点A',使 连接CA',则△CDA'即为所求.
(2)根据中心对称的性质可知△ADB≌ 5+7,即2<2AD<12.∴1
1. C 2. A 3. C 4.2cm 24cm 5.2
6.解:如图所示,点O 为对称中心.
7. D 8. B 9.4
10.解:如图所示((2)中平分面积的方法不唯一).
23.2.3 关于原点对称的点的坐标1. D 2. D 3.(0,-3)
4. B 【变式题】A 5.-2
7. A 8. C 9.一10.(-5,-3)
11.解:(1)根据对称中心的性质,可得对称中心是 D D 的中点.∵D ,D 的坐标分别是(0,3),(0,2),∴对称中心的坐标是(0,2.5).
(2)∵A,D 的坐标分别是(0,4),(0,2),∴正方形 ABCD 与正方形 A B C D 的边长都是4-2=2.∴B,C的坐标分别是(-2,4),(--2,2).∵A D =2,D 的坐标是(0,3),∴A 的坐标是(0,1).∴B ,C 的坐标分别是(2,1),(2,3).综上所述,可得顶点 B,C,B ,C 的坐标分别是(-2,4),(-2,2),(2,1),(2,3).
同课章节目录
