北师大版六年级下册数学《《总复习——式与方程》》课件(共44张PPT)
文档属性
| 名称 | 北师大版六年级下册数学《《总复习——式与方程》》课件(共44张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-03 00:00:00 | ||
图片预览









文档简介
(共44张PPT)
总复习(四)
北师大版 小学六年级数学下册
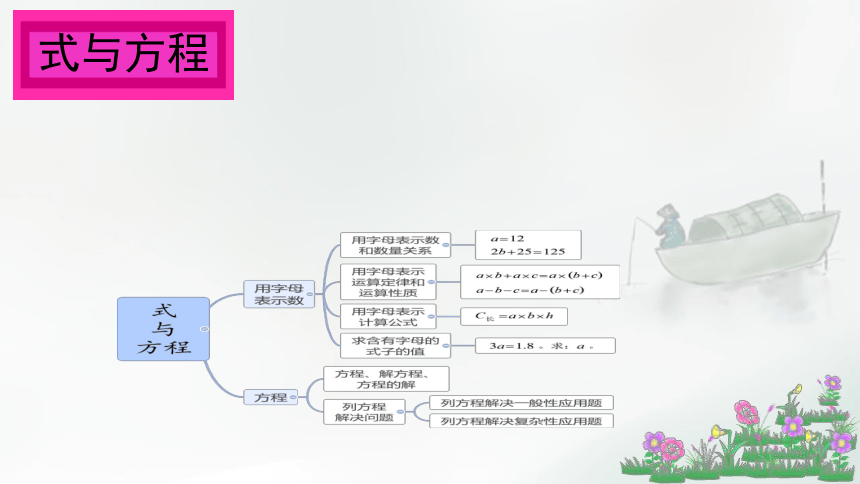
式与方程
式与方程
用字母表示数和数量关系
1. 用字母或含有字母的式子表示数:
例1:学校买来 b 本新书,平均分给三年级 d 个班,每班分得多少本新书?
例2:小明有 a 张邮票,小刚有 b 张邮票,小明比小刚少多少张邮票?
在同一个式子里,同一个字母只能表示同一个数,不同的数可以用
不同的字母表示。
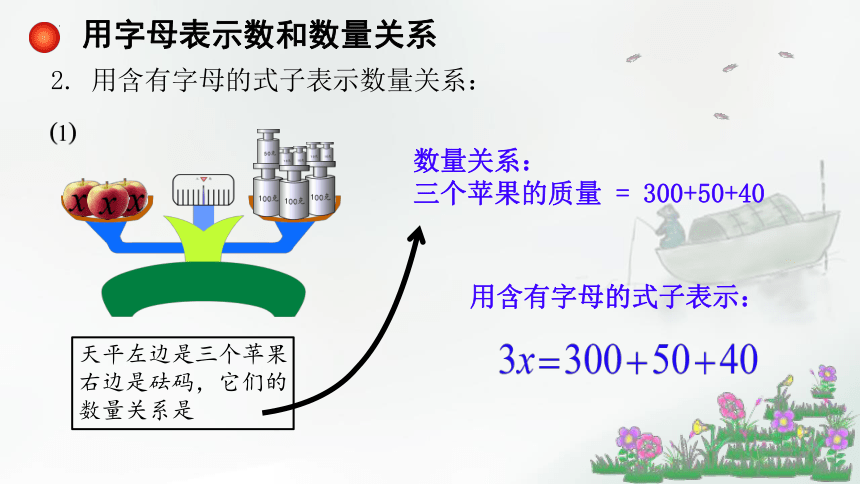
用字母表示数和数量关系
2. 用含有字母的式子表示数量关系:
数量关系:
三个苹果的质量 = 300+50+40
用含有字母的式子表示:
天平左边是三个苹果
右边是砝码,它们的
数量关系是
用字母表示数和数量关系
2. 用含有字母的式子表示数量关系:
(2) 学校食堂购进1500千克大米,每天吃 b 千克,吃了 a 天,还剩下
多少千克大米?
(3)
!
!
!
我
们
学
过
的
运
算
定
律
也
可
以
用
字
母
来
表
示
的
加法交换律:
加法结合律:
乘法交换律:
乘法结合律:
乘法分配律:
连减:
连除:
用字母表示数和数量关系
3. 用含有字母的式子表示公式:
(1)长方形的周长
用字母表示:
用字母表示数和数量关系
3. 用含有字母的式子表示公式:
(2)正方形的周长
用字母表示:
用字母表示数和数量关系
3. 用含有字母的式子表示公式:
(3)圆的周长
用字母表示:
d
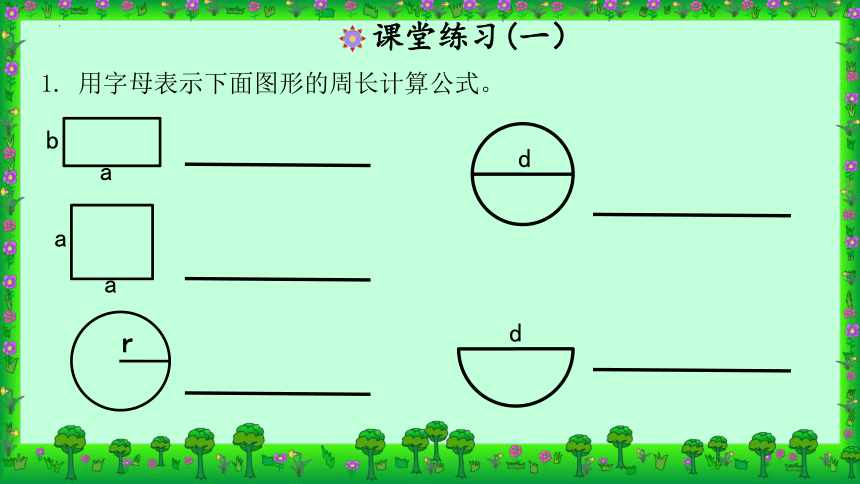
课堂练习(一)
1. 用字母表示下面图形的周长计算公式。
r
d
a
b
a
a
用字母表示数和数量关系
3. 用含有字母的式子表示公式:
(4)长方形的面积
用字母表示:
用字母表示数和数量关系
3. 用含有字母的式子表示公式:
(5)正方形的面积
用字母表示
用字母表示数和数量关系
3. 用含有字母的式子表示公式:
(6)三角形的面积
用字母表示
用字母表示数、数量关系
3. 用含有字母的式子表示公式:
(7)平行四边形的面积
用字母表示
用字母表示数、数量关系
3. 用含有字母的式子表示公式:
(8)梯形的面积
用字母表示
用字母表示数、数量关系
3. 用含有字母的式子表示公式:
(9)圆的面积
用字母表示
课堂练习(二)
2. 用字母表示下面图形的面积计算公式。
用字母表示数、数量关系
3. 用含有字母的式子表示公式:
(10)长方体的体积
用字母表示
用字母表示数、数量关系
3. 用含有字母的式子表示公式:
(11)正方体的体积
用字母表示
用字母表示数、数量关系
3. 用含有字母的式子表示公式:
(12)圆柱的体积
用字母表示
用字母表示数、数量关系
3. 用含有字母的式子表示公式:
(13)圆锥的体积
用字母表示
课堂练习(三)
3. 用字母表示下面图形的体积计算公式。
用字母表示式子的读法和写法
例如:
读法:
在含有字母的式子里,字母就读
字母名称。
写法:
字母与数字之间,字母与字母
之间的乘号通常是省略不写,其
中数字一定写在字母的前面。
难点:
等式和方程
等式和方程的意义与关系:
1. 表示相等关系的式子叫等式。例如:
2. 含有未知数的等式叫做方程。例如:
3. 所有的方程都是等式,但等式不全是方程,二者关系如下:
方程
等式
课堂练习(四)
1. 用字母表示运算定律。
加法交换律:
乘法交换律:
乘法分配律:
加法结合律:
乘法结合律:
2. 填空题。
方程的解和解方程
1.方程的解:使方程左右两边相等的未知数的值,叫作方程的解。
例如:
2. 解方程:求方程的解的过程叫作解方程。例如:
方程的解和解方程
解:
易错点:方程的解是一个值,如: ;解方程是一个
演算过程。
课堂练习(五)
1. 解方程。
完成课本
81页第5题
解:
解:
解:
解:
解:
解:
列方程解决问题
1. 列方程解决一般应用题。
步骤:
1)分析题意,明确题目中的数量关系。
2)一般用 表示题中未知数。设未知数的方法有两种:一种是直接
设定,题目求什么数就设什么数为 ;另一种是间接设定,先设与未
知数相关的一个数为 ,再通过这个数去求所求的数。
列方程解决问题
1. 列方程解决一般应用题。
1)水果店购进20箱苹果,购进苹果的箱数是桔子箱数的 。
水果店购进多少箱桔子?
数量关系:桔子箱数的 = 苹果的箱数
解:设水果店购进 箱桔子。
例题:
列方程解决问题
1. 列方程解决一般应用题。
例题:
2)妙想和乐乐一共收集了128枚邮票。妙想收集的邮票
是乐乐的 3 倍。妙想、乐乐各收集了多少枚出票?
数量关系:
解:设乐乐收集了 枚邮票。那么妙想的邮票就是 。
课堂练习(六)
1. 杭州湾大桥全长36千米,比香港青马大桥的16倍还多0.8千米。香港
青马大桥全长多少千米?
2. 一张桌子和一把椅子共卖245元,已知一张桌子的价格是一把椅子的
4倍。一张桌子多少元?
3. 两地之间的距离是300千米,A、B两客车同时从两地相向开出,2.5小
时后两车还相距50千米。已知A客车每小时行45千米。B 客车每小时行
多少千米?
列方程解决问题
2. 列方程解决等量关系复杂的应用题
盈亏问题、比例问题、浓度问题。
盈亏问题
盈亏问题:是把若干个物体平均分给一定数量的对象,但不是
每次都能分完,如果物体有剩余就叫“盈”,如果物体不够分
就叫“亏”。列方程的依据是:分配方式不同,但物体的总量
是不变的。
例:1
同学们种树苗绿化校园。如果每个同学种3棵树苗,则还剩余3棵;
如果每个同学种4棵树苗,则还差2棵树苗。参加种树的有多少名
同学?一共有多少棵树苗?
列方程解决问题
2. 列方程解决等量关系复杂的应用题
例题:2
同学们种树苗绿化校园。如果每个同学种3棵树苗,则还剩余3棵;
如果每个同学种4棵树苗,则还差2棵树苗。参加种树的有多少名
同学?一共有多少棵树苗?
题意分析
题目中种树的分配方案不同,但树苗的总数量和同学的总人数不变。
根据题意可以设同学人数为 。
解:设参加种树的同学有 名。
例题:3
A款西服,如果按定价打九折销售可以获利70元,如果按定价打九五
折销售可以获利120元。这种西服的进货价是多少元?
题意分析
题目中西服的进货价和定价是不变的,根据题意可以设定价为 。
解:设西服的定价为 。
进货价:
课堂练习(七)
1、陈老师给小朋友分饼干,每人分3块要多出5块,如果每人分4块还差 8块。问小朋友有 多少人?饼干有多少块?
2、某招待所开会,每个房间住3人则多26人,每个房间住4人则还多13人, 如果每个房间住5人。那么情况又怎么样
3、小红拿着一根绳子来测量一根树的树干周长,将绳子3折,围了一圈多 3分米 ,将绳子4 折,围了一圈还差7分米不够长,问绳子长和树干的 周长各是多少?
比例问题
1.已知总量与各部分量的比,求各部分量。
2.已知各部分量的差与各部分量的比,求各部分量。
3.已知一部分量与各部分量的比,求另一部分量或总量。
例题1)
甲组和乙组的人数比是5:3,如果从甲组调14人到乙组去,那么甲
组和乙组的人数比是1:2,原来甲、乙两组各有多少人?
分析:
题目中的数量关系是:(甲组人数 -14):(乙组人数 +14)=1:2。
而原有甲组人数:乙组人数 =5:3,因此可以设原有每份人数为 ,
则甲组原有5 人,乙组原有3 人。
解:设原有每份人数为 人,则甲组原有5 人,乙组原有3 人。
例题2)
实验小学乒乓球活动小组的女生人数占总人数的 ,新学期又加入
4名女生,这时女生人数占总人数的 ,现在乒乓球活动小组有学生
多少人?
分析:
题目中,女生人数+4=总人数的 ,因此可以设现在乒乓活动小组有
女生 人,那么原来小组女生人数为 。由此得出:原来女
生人数+新加入的女生人数=现在女生人数。
解:设现在乒乓球活动小组有学生 人。
课堂练习(八)
1.甲、乙两人原有的钱数比是6:5,后来甲又得到180元,乙又得到30元,
这时两人的钱数比是18:11。求原来两的钱数之和是多少?
2.端午节食堂买来两桶粽子,乙桶的粽子个数是甲桶的 ,从甲桶中取
出39个粽子放入乙桶中,这时乙桶的粽子个数是甲桶的 。求乙桶中
原有粽子多少个?
浓度问题
浓度:通常用溶质占溶液质量的百分比来表示,常见的浓度总量
有:稀释、提高浓度两种。
1.稀释。加入溶剂(比如水),使浓度下降达到稀释效果。可以
根据溶质的质量不变来列方程。
2.提高浓度。分两种情况:一种是加入溶质,使浓度提高。可以
根据加入溶质前后的溶剂(比如水)的质量不变来列方程。
第二种是蒸发水分,以达到浓度提高。可以根据溶质的质量不变
来列方程。
课堂练习(九)
1、要把30克含盐16%的盐水稀释成含盐0.15%的盐水,须加水多少克?
2、现有含盐12.5%的盐水40千克,要蒸去多少水分才能制出含盐20% 的盐水?
3、现在要配制治棉铃虫0.05%的“1059”溶液,请问在599千克水中,
应加入30%的“1059”溶液多少千克?
总复习(四)
北师大版 小学六年级数学下册
式与方程
式与方程
用字母表示数和数量关系
1. 用字母或含有字母的式子表示数:
例1:学校买来 b 本新书,平均分给三年级 d 个班,每班分得多少本新书?
例2:小明有 a 张邮票,小刚有 b 张邮票,小明比小刚少多少张邮票?
在同一个式子里,同一个字母只能表示同一个数,不同的数可以用
不同的字母表示。
用字母表示数和数量关系
2. 用含有字母的式子表示数量关系:
数量关系:
三个苹果的质量 = 300+50+40
用含有字母的式子表示:
天平左边是三个苹果
右边是砝码,它们的
数量关系是
用字母表示数和数量关系
2. 用含有字母的式子表示数量关系:
(2) 学校食堂购进1500千克大米,每天吃 b 千克,吃了 a 天,还剩下
多少千克大米?
(3)
!
!
!
我
们
学
过
的
运
算
定
律
也
可
以
用
字
母
来
表
示
的
加法交换律:
加法结合律:
乘法交换律:
乘法结合律:
乘法分配律:
连减:
连除:
用字母表示数和数量关系
3. 用含有字母的式子表示公式:
(1)长方形的周长
用字母表示:
用字母表示数和数量关系
3. 用含有字母的式子表示公式:
(2)正方形的周长
用字母表示:
用字母表示数和数量关系
3. 用含有字母的式子表示公式:
(3)圆的周长
用字母表示:
d
课堂练习(一)
1. 用字母表示下面图形的周长计算公式。
r
d
a
b
a
a
用字母表示数和数量关系
3. 用含有字母的式子表示公式:
(4)长方形的面积
用字母表示:
用字母表示数和数量关系
3. 用含有字母的式子表示公式:
(5)正方形的面积
用字母表示
用字母表示数和数量关系
3. 用含有字母的式子表示公式:
(6)三角形的面积
用字母表示
用字母表示数、数量关系
3. 用含有字母的式子表示公式:
(7)平行四边形的面积
用字母表示
用字母表示数、数量关系
3. 用含有字母的式子表示公式:
(8)梯形的面积
用字母表示
用字母表示数、数量关系
3. 用含有字母的式子表示公式:
(9)圆的面积
用字母表示
课堂练习(二)
2. 用字母表示下面图形的面积计算公式。
用字母表示数、数量关系
3. 用含有字母的式子表示公式:
(10)长方体的体积
用字母表示
用字母表示数、数量关系
3. 用含有字母的式子表示公式:
(11)正方体的体积
用字母表示
用字母表示数、数量关系
3. 用含有字母的式子表示公式:
(12)圆柱的体积
用字母表示
用字母表示数、数量关系
3. 用含有字母的式子表示公式:
(13)圆锥的体积
用字母表示
课堂练习(三)
3. 用字母表示下面图形的体积计算公式。
用字母表示式子的读法和写法
例如:
读法:
在含有字母的式子里,字母就读
字母名称。
写法:
字母与数字之间,字母与字母
之间的乘号通常是省略不写,其
中数字一定写在字母的前面。
难点:
等式和方程
等式和方程的意义与关系:
1. 表示相等关系的式子叫等式。例如:
2. 含有未知数的等式叫做方程。例如:
3. 所有的方程都是等式,但等式不全是方程,二者关系如下:
方程
等式
课堂练习(四)
1. 用字母表示运算定律。
加法交换律:
乘法交换律:
乘法分配律:
加法结合律:
乘法结合律:
2. 填空题。
方程的解和解方程
1.方程的解:使方程左右两边相等的未知数的值,叫作方程的解。
例如:
2. 解方程:求方程的解的过程叫作解方程。例如:
方程的解和解方程
解:
易错点:方程的解是一个值,如: ;解方程是一个
演算过程。
课堂练习(五)
1. 解方程。
完成课本
81页第5题
解:
解:
解:
解:
解:
解:
列方程解决问题
1. 列方程解决一般应用题。
步骤:
1)分析题意,明确题目中的数量关系。
2)一般用 表示题中未知数。设未知数的方法有两种:一种是直接
设定,题目求什么数就设什么数为 ;另一种是间接设定,先设与未
知数相关的一个数为 ,再通过这个数去求所求的数。
列方程解决问题
1. 列方程解决一般应用题。
1)水果店购进20箱苹果,购进苹果的箱数是桔子箱数的 。
水果店购进多少箱桔子?
数量关系:桔子箱数的 = 苹果的箱数
解:设水果店购进 箱桔子。
例题:
列方程解决问题
1. 列方程解决一般应用题。
例题:
2)妙想和乐乐一共收集了128枚邮票。妙想收集的邮票
是乐乐的 3 倍。妙想、乐乐各收集了多少枚出票?
数量关系:
解:设乐乐收集了 枚邮票。那么妙想的邮票就是 。
课堂练习(六)
1. 杭州湾大桥全长36千米,比香港青马大桥的16倍还多0.8千米。香港
青马大桥全长多少千米?
2. 一张桌子和一把椅子共卖245元,已知一张桌子的价格是一把椅子的
4倍。一张桌子多少元?
3. 两地之间的距离是300千米,A、B两客车同时从两地相向开出,2.5小
时后两车还相距50千米。已知A客车每小时行45千米。B 客车每小时行
多少千米?
列方程解决问题
2. 列方程解决等量关系复杂的应用题
盈亏问题、比例问题、浓度问题。
盈亏问题
盈亏问题:是把若干个物体平均分给一定数量的对象,但不是
每次都能分完,如果物体有剩余就叫“盈”,如果物体不够分
就叫“亏”。列方程的依据是:分配方式不同,但物体的总量
是不变的。
例:1
同学们种树苗绿化校园。如果每个同学种3棵树苗,则还剩余3棵;
如果每个同学种4棵树苗,则还差2棵树苗。参加种树的有多少名
同学?一共有多少棵树苗?
列方程解决问题
2. 列方程解决等量关系复杂的应用题
例题:2
同学们种树苗绿化校园。如果每个同学种3棵树苗,则还剩余3棵;
如果每个同学种4棵树苗,则还差2棵树苗。参加种树的有多少名
同学?一共有多少棵树苗?
题意分析
题目中种树的分配方案不同,但树苗的总数量和同学的总人数不变。
根据题意可以设同学人数为 。
解:设参加种树的同学有 名。
例题:3
A款西服,如果按定价打九折销售可以获利70元,如果按定价打九五
折销售可以获利120元。这种西服的进货价是多少元?
题意分析
题目中西服的进货价和定价是不变的,根据题意可以设定价为 。
解:设西服的定价为 。
进货价:
课堂练习(七)
1、陈老师给小朋友分饼干,每人分3块要多出5块,如果每人分4块还差 8块。问小朋友有 多少人?饼干有多少块?
2、某招待所开会,每个房间住3人则多26人,每个房间住4人则还多13人, 如果每个房间住5人。那么情况又怎么样
3、小红拿着一根绳子来测量一根树的树干周长,将绳子3折,围了一圈多 3分米 ,将绳子4 折,围了一圈还差7分米不够长,问绳子长和树干的 周长各是多少?
比例问题
1.已知总量与各部分量的比,求各部分量。
2.已知各部分量的差与各部分量的比,求各部分量。
3.已知一部分量与各部分量的比,求另一部分量或总量。
例题1)
甲组和乙组的人数比是5:3,如果从甲组调14人到乙组去,那么甲
组和乙组的人数比是1:2,原来甲、乙两组各有多少人?
分析:
题目中的数量关系是:(甲组人数 -14):(乙组人数 +14)=1:2。
而原有甲组人数:乙组人数 =5:3,因此可以设原有每份人数为 ,
则甲组原有5 人,乙组原有3 人。
解:设原有每份人数为 人,则甲组原有5 人,乙组原有3 人。
例题2)
实验小学乒乓球活动小组的女生人数占总人数的 ,新学期又加入
4名女生,这时女生人数占总人数的 ,现在乒乓球活动小组有学生
多少人?
分析:
题目中,女生人数+4=总人数的 ,因此可以设现在乒乓活动小组有
女生 人,那么原来小组女生人数为 。由此得出:原来女
生人数+新加入的女生人数=现在女生人数。
解:设现在乒乓球活动小组有学生 人。
课堂练习(八)
1.甲、乙两人原有的钱数比是6:5,后来甲又得到180元,乙又得到30元,
这时两人的钱数比是18:11。求原来两的钱数之和是多少?
2.端午节食堂买来两桶粽子,乙桶的粽子个数是甲桶的 ,从甲桶中取
出39个粽子放入乙桶中,这时乙桶的粽子个数是甲桶的 。求乙桶中
原有粽子多少个?
浓度问题
浓度:通常用溶质占溶液质量的百分比来表示,常见的浓度总量
有:稀释、提高浓度两种。
1.稀释。加入溶剂(比如水),使浓度下降达到稀释效果。可以
根据溶质的质量不变来列方程。
2.提高浓度。分两种情况:一种是加入溶质,使浓度提高。可以
根据加入溶质前后的溶剂(比如水)的质量不变来列方程。
第二种是蒸发水分,以达到浓度提高。可以根据溶质的质量不变
来列方程。
课堂练习(九)
1、要把30克含盐16%的盐水稀释成含盐0.15%的盐水,须加水多少克?
2、现有含盐12.5%的盐水40千克,要蒸去多少水分才能制出含盐20% 的盐水?
3、现在要配制治棉铃虫0.05%的“1059”溶液,请问在599千克水中,
应加入30%的“1059”溶液多少千克?
