人教版初中数学九年级下册同步课件 第二十八章-锐角三角函数章末总结(共17张PPT)
文档属性
| 名称 | 人教版初中数学九年级下册同步课件 第二十八章-锐角三角函数章末总结(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 665.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-05 20:14:11 | ||
图片预览



文档简介
课件17张PPT。第二十八章
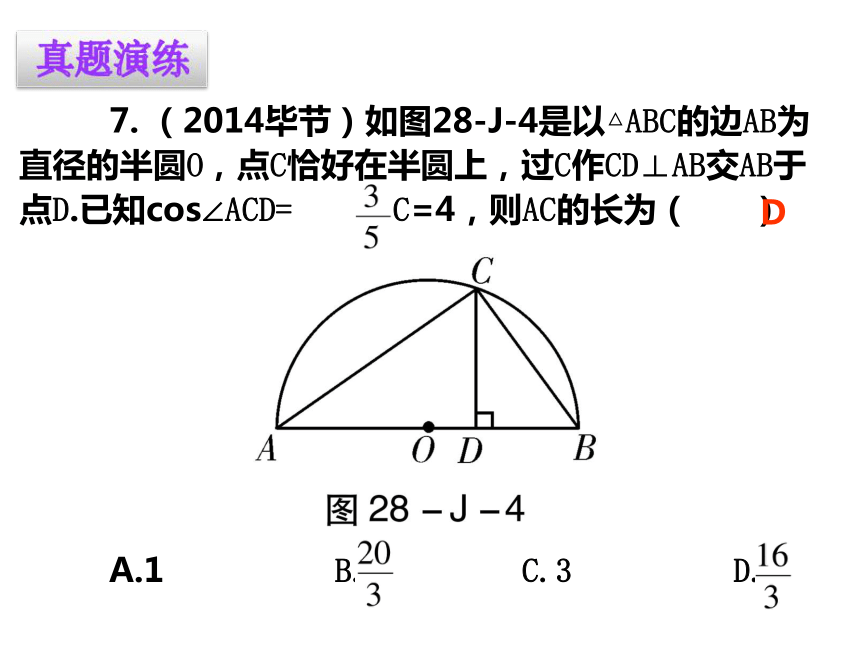
锐角三角函数章末总结 7. (2014毕节)如图28-J-4是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB交AB于点D.已知cos∠ACD= ,BC=4,则AC的长为( )
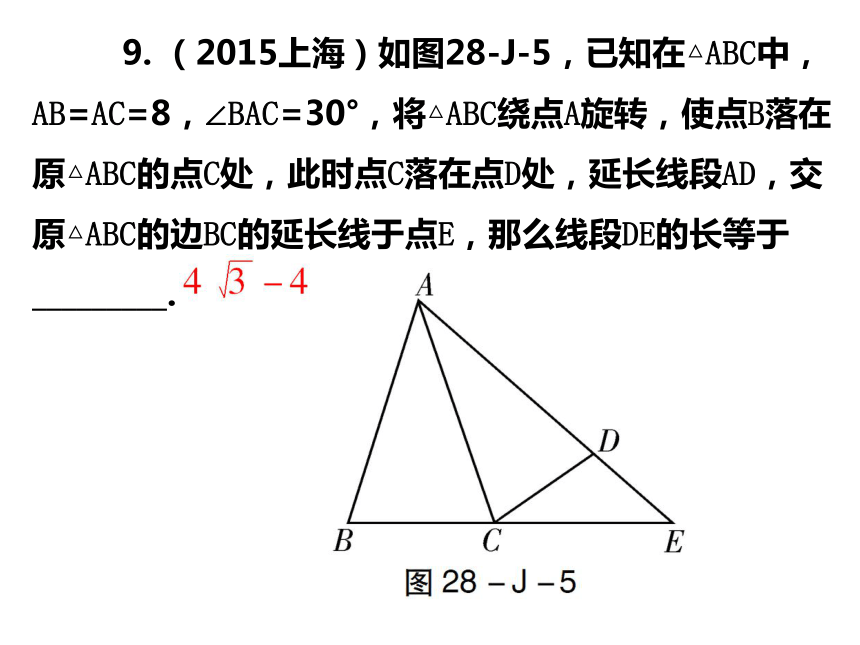
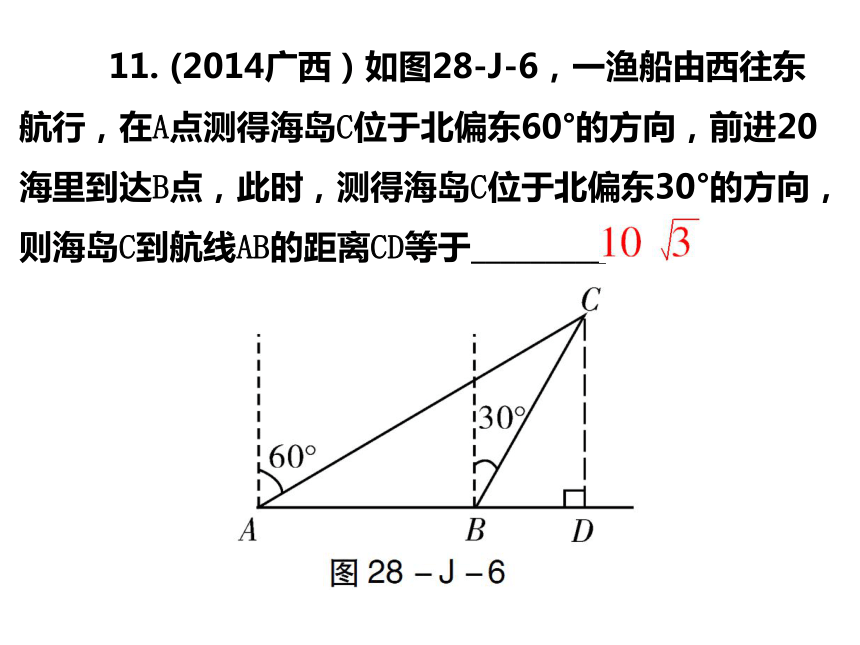
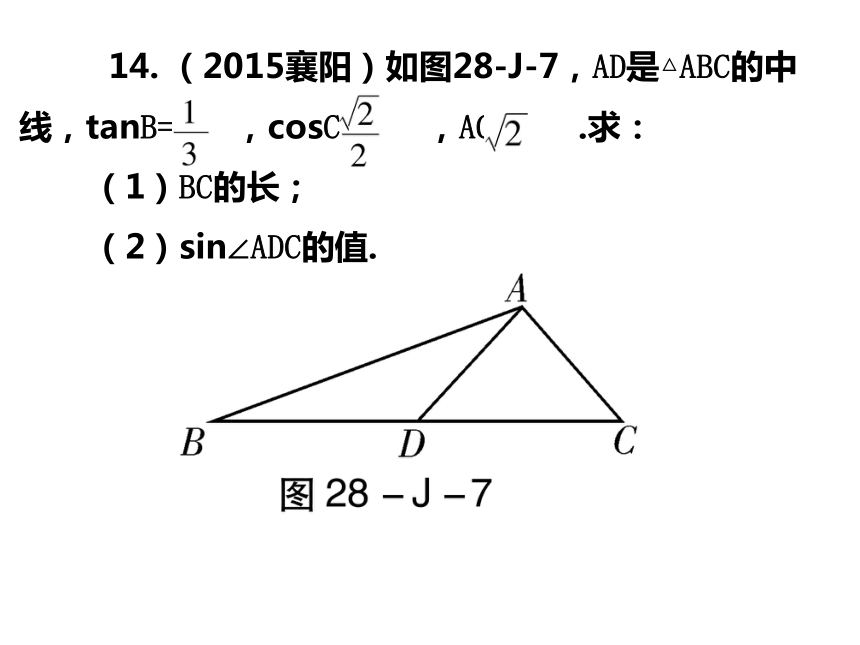
A.1 B. C.3 D.D 9. (2015上海)如图28-J-5,已知在△ABC中,AB=AC=8,∠BAC=30°,将△ABC绕点A旋转,使点B落在原△ABC的点C处,此时点C落在点D处,延长线段AD,交原△ABC的边BC的延长线于点E,那么线段DE的长等于_________. 11. (2014广西)如图28-J-6,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于_________海里. 14. (2015襄阳)如图28-J-7,AD是△ABC的中线,tanB= ,cosC= ,AC= .求:
(1)BC的长;
(2)sin∠ADC的值. 15. (2015资阳)北京时间
2015年04月25日14时11分,尼泊
尔发生8.1级强烈地震,我国积极
组织抢险队赴地震灾区参与抢险
工作.如图28-J-8,某探测队在地
面A,B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4 m,求该生命迹象所在位置C的深度.(结果精确到1 m.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,
≈1.7) 16. (2013北京)如图28-J-9,
AB是⊙O的直径,PA,PC与⊙O分
别相切于点A,C,PC交AB的延长
线于点D,DE⊥PO交PO的延长线
于点E.
(1)求证:∠EPD=∠EDO;
(2)若PC=6,tan∠PDA= ,求OE的长. (1)证明:PA,PC与⊙O分别相切于点A,C.
∴∠APO=∠EPD,且PA⊥AO.
∴∠PAO=90°.
∵∠AOP=∠EOD,∠PAO=∠E=90°,
∴∠APO=∠EDO.
∴∠EPD=∠EDO. 17. (2014聊城)已知:
如图28-J-10,在△ABC中,
AB=BC,D是AC的中点,BE
平分∠ABD交AC于点E,点
O是AB上一点,⊙O过B,E
两点,交BD于点G,交AB于点F.
(1)求证:AC与⊙O相切;
(2)当BD=6,sinC= 时,求⊙O的半径. (1)证明:如答图28-J-4,
连接OE.
∵AB=BC且D是AC中点,
∴BD⊥AC.
∵BE平分∠ABD,∴∠ABE=∠DBE.
∵OB=OE,
∴∠OBE=∠OEB.∴∠OEB=∠DBE.∴OE∥BD.
∵BD⊥AC,∴OE⊥AC.
∵OE为⊙O半径,∴AC与⊙O相切.
锐角三角函数章末总结 7. (2014毕节)如图28-J-4是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB交AB于点D.已知cos∠ACD= ,BC=4,则AC的长为( )
A.1 B. C.3 D.D 9. (2015上海)如图28-J-5,已知在△ABC中,AB=AC=8,∠BAC=30°,将△ABC绕点A旋转,使点B落在原△ABC的点C处,此时点C落在点D处,延长线段AD,交原△ABC的边BC的延长线于点E,那么线段DE的长等于_________. 11. (2014广西)如图28-J-6,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于_________海里. 14. (2015襄阳)如图28-J-7,AD是△ABC的中线,tanB= ,cosC= ,AC= .求:
(1)BC的长;
(2)sin∠ADC的值. 15. (2015资阳)北京时间
2015年04月25日14时11分,尼泊
尔发生8.1级强烈地震,我国积极
组织抢险队赴地震灾区参与抢险
工作.如图28-J-8,某探测队在地
面A,B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4 m,求该生命迹象所在位置C的深度.(结果精确到1 m.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,
≈1.7) 16. (2013北京)如图28-J-9,
AB是⊙O的直径,PA,PC与⊙O分
别相切于点A,C,PC交AB的延长
线于点D,DE⊥PO交PO的延长线
于点E.
(1)求证:∠EPD=∠EDO;
(2)若PC=6,tan∠PDA= ,求OE的长. (1)证明:PA,PC与⊙O分别相切于点A,C.
∴∠APO=∠EPD,且PA⊥AO.
∴∠PAO=90°.
∵∠AOP=∠EOD,∠PAO=∠E=90°,
∴∠APO=∠EDO.
∴∠EPD=∠EDO. 17. (2014聊城)已知:
如图28-J-10,在△ABC中,
AB=BC,D是AC的中点,BE
平分∠ABD交AC于点E,点
O是AB上一点,⊙O过B,E
两点,交BD于点G,交AB于点F.
(1)求证:AC与⊙O相切;
(2)当BD=6,sinC= 时,求⊙O的半径. (1)证明:如答图28-J-4,
连接OE.
∵AB=BC且D是AC中点,
∴BD⊥AC.
∵BE平分∠ABD,∴∠ABE=∠DBE.
∵OB=OE,
∴∠OBE=∠OEB.∴∠OEB=∠DBE.∴OE∥BD.
∵BD⊥AC,∴OE⊥AC.
∵OE为⊙O半径,∴AC与⊙O相切.
