人教版初中数学九年级下册同步课件 29.2 三视图(共28张PPT)
文档属性
| 名称 | 人教版初中数学九年级下册同步课件 29.2 三视图(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 715.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-05 20:17:25 | ||
图片预览






文档简介
课件28张PPT。第二十九章
投影与视图29.2
三视图 新知1 三视图
(1)主视图反映物体的高和长,俯视图反映物体的长和宽,左视图反映物体的高和宽.
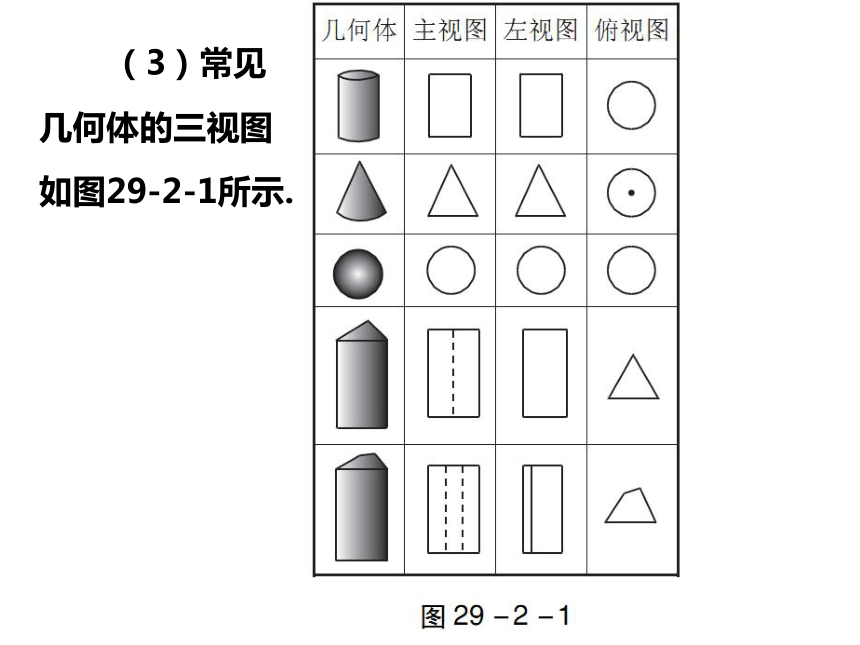
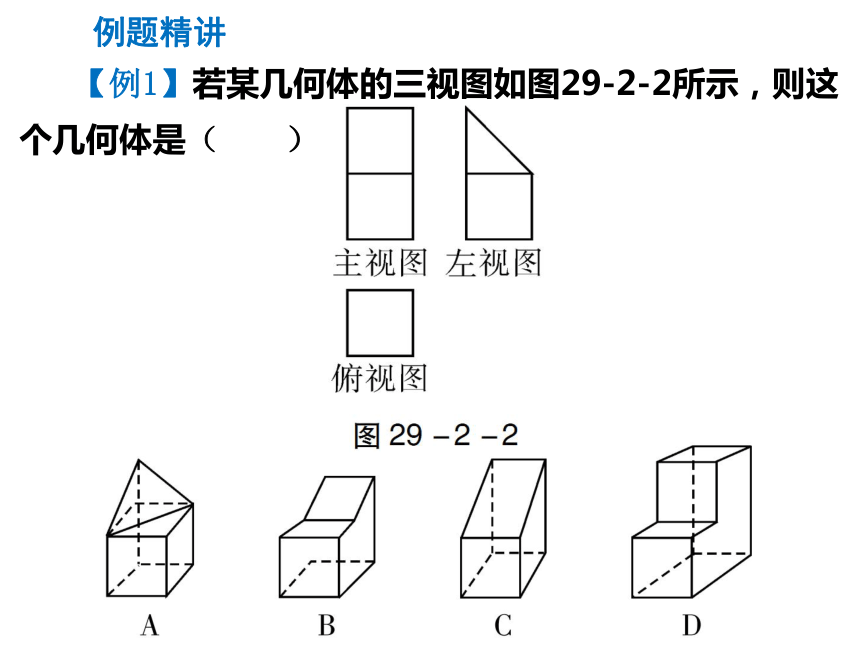
(2)三视图与投影的关系密切,某些物体的三视图实际上是该物体在一定条件下所形成的平行投影,某些物体的主视图、左视图、俯视图可以看成在一束平行光线分别从物体的正面、左面、上面照射下,在垂直于这一方向的平面上所形成的投影. (3)常见几何体的三视图如图29-2-1所示. 【例1】若某几何体的三视图如图29-2-2所示,则这个几何体是( ) 例题精讲 解析 该几何体的正视图与俯视图均为矩形,侧视图为三角形和一个矩形,易得出该几何体的形状.
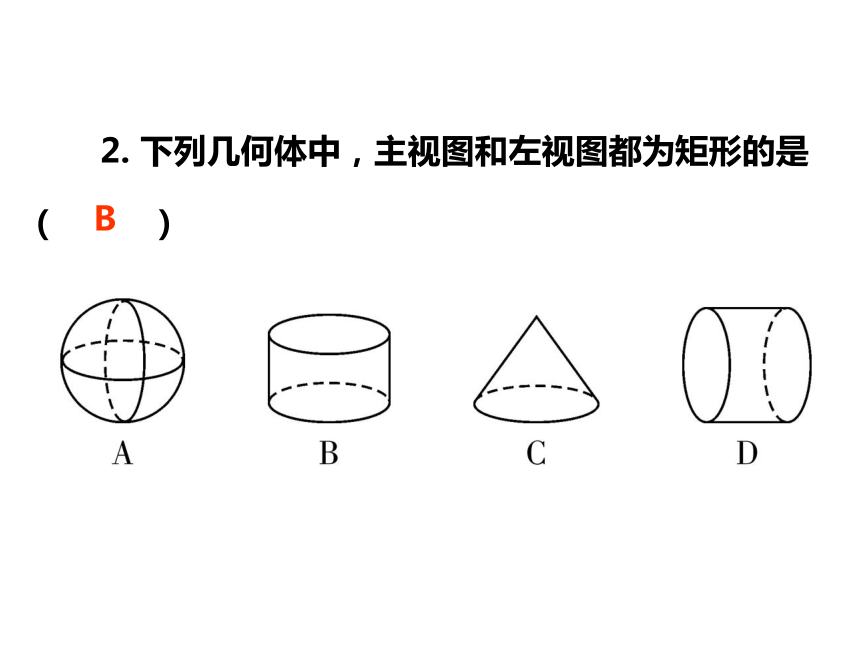
答案 C 1. 下面几个几何体,主视图是圆的是( ) 举一反三B 2. 下列几何体中,主视图和左视图都为矩形的是( )B 新知2 画几何体的三视图
(1)画三视图时,要保证:主视图与俯视图的长对正、主视图与左视图的高平齐、左视图与俯视图的宽相等,简称为“主与俯长对正,主与左高平齐,左与俯宽相等”.
(2)在画视图时,一定要将边缘、棱、顶点都体现出来,看得见的轮廓线画成实线,看不见的轮廓线画成虚线. 【例2】如图29-2-3是一个几何体,请你画出它的三视图. 例题精讲 解析 本题中的几何体是正方体被切去一块,要合理想象,并注意可看到的轮廓线用实线,看不到的用虚线.
解 如图29-2-4是该几何体的三视图. 1. 画出图29-2-5中图形的三视图. 举一反三 如答图29-2-1所示. 新知3 由三视图到立体图
由三视图确定物体的形状要根据各视图从各个方向看到的几何体形状,在综合确定几何体的形状时,遵循的原则是长对正,高平齐,宽相等. 【例3】如图29-2-6是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要个小立方块. 例题精讲 解析 由俯视图易得最底层有7个小立方体,由主视图知,第二层有2个小立方体,第三层有1个小立方体,那么共有7+2+1=10个几何体组成.若搭成一个大正方体,共需4×4×4=64个小立方体,所以还需64-10=54个小立方体.
答案 54 如图29-2-7所示,
是一些完全相同的小正
方体搭成的几何体的三
视图.这个几何体只能是( )
举一反三A 新知4 三视图与几何体的体积和表面积的综合应用 【例4】如图29-2-8是某几何体的三视图,根据图中数据,可得该几何体的体积
为( )
A. 60π
B. 70π
C. 90π
D. 160π 例题精讲 解析 易得此几何体为空心圆柱,圆柱的体积=底面积×高,把相关数值代入即可求解
观察三视图发现该几何体为空心圆柱,其内径为3,外径为4,高为10,
所以其体积为10×(42π-32π)=70π.
答案 B 1. 由若干个边长为1 cm的正方体堆积成一个几何体,它的三视图如图29-2-9所示,则这个几何体的表面积是( )
A. 15 cm2
B. 18 cm2
C. 21 cm2
D. 24 cm2 举一反三B 2. 已知某几何体的三视图如图29-2-10所示,则该几何体的体积为( )B 1. 三视图的摆放规则:俯视图放在主视图的下面,长度与主视图的长度一样;左视图放在主视图的右面,高度与主视图的高度一样,宽度与俯视图的宽度一样,可简记为“长对正;高平齐;宽相等”.
2. 在画物体的三视图时,对看得见的轮廓线用实线画出,而对看不见的轮廓线要用虚线画出.在三种视图中,主视图反映的是物体的长和高,俯视图反映的是物体的长和宽,左视图反映的是物体的宽和高.因此,在画三视图时,对应部分的长度要相等. 方法规律 7. (6分)如图KT29-2-6,
是一个由若干个棱长相等的正方
体构成的几何体的三视图.
(1)请写出构成这个几何体的
正方体个数;
(2)请根据图中所标的尺寸,
计算这个几何体的表面积. 解:(1)5个.
(2)S表=5×6a2-2×5a2=20a2. 8. (6分)如图KT29-2-7
是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据图中所示数据计算
这个几何体的表面积;
(3)如果一只蚂蚁要从这个
几何体中的点B出发,沿表面爬
到AC的中点D,请你求出这个线路的最短路程. 解:(1)圆锥.
(2)S表=S扇形+S圆=πrl+
πr2=12π+4π=16π(cm2).
(3)如答图29-2-2将圆锥侧面展开,线段BD为所求的最短路程.
由条件得,∠BAB′=120°,C为弧BB′中点,所以BD= (cm).
投影与视图29.2
三视图 新知1 三视图
(1)主视图反映物体的高和长,俯视图反映物体的长和宽,左视图反映物体的高和宽.
(2)三视图与投影的关系密切,某些物体的三视图实际上是该物体在一定条件下所形成的平行投影,某些物体的主视图、左视图、俯视图可以看成在一束平行光线分别从物体的正面、左面、上面照射下,在垂直于这一方向的平面上所形成的投影. (3)常见几何体的三视图如图29-2-1所示. 【例1】若某几何体的三视图如图29-2-2所示,则这个几何体是( ) 例题精讲 解析 该几何体的正视图与俯视图均为矩形,侧视图为三角形和一个矩形,易得出该几何体的形状.
答案 C 1. 下面几个几何体,主视图是圆的是( ) 举一反三B 2. 下列几何体中,主视图和左视图都为矩形的是( )B 新知2 画几何体的三视图
(1)画三视图时,要保证:主视图与俯视图的长对正、主视图与左视图的高平齐、左视图与俯视图的宽相等,简称为“主与俯长对正,主与左高平齐,左与俯宽相等”.
(2)在画视图时,一定要将边缘、棱、顶点都体现出来,看得见的轮廓线画成实线,看不见的轮廓线画成虚线. 【例2】如图29-2-3是一个几何体,请你画出它的三视图. 例题精讲 解析 本题中的几何体是正方体被切去一块,要合理想象,并注意可看到的轮廓线用实线,看不到的用虚线.
解 如图29-2-4是该几何体的三视图. 1. 画出图29-2-5中图形的三视图. 举一反三 如答图29-2-1所示. 新知3 由三视图到立体图
由三视图确定物体的形状要根据各视图从各个方向看到的几何体形状,在综合确定几何体的形状时,遵循的原则是长对正,高平齐,宽相等. 【例3】如图29-2-6是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要个小立方块. 例题精讲 解析 由俯视图易得最底层有7个小立方体,由主视图知,第二层有2个小立方体,第三层有1个小立方体,那么共有7+2+1=10个几何体组成.若搭成一个大正方体,共需4×4×4=64个小立方体,所以还需64-10=54个小立方体.
答案 54 如图29-2-7所示,
是一些完全相同的小正
方体搭成的几何体的三
视图.这个几何体只能是( )
举一反三A 新知4 三视图与几何体的体积和表面积的综合应用 【例4】如图29-2-8是某几何体的三视图,根据图中数据,可得该几何体的体积
为( )
A. 60π
B. 70π
C. 90π
D. 160π 例题精讲 解析 易得此几何体为空心圆柱,圆柱的体积=底面积×高,把相关数值代入即可求解
观察三视图发现该几何体为空心圆柱,其内径为3,外径为4,高为10,
所以其体积为10×(42π-32π)=70π.
答案 B 1. 由若干个边长为1 cm的正方体堆积成一个几何体,它的三视图如图29-2-9所示,则这个几何体的表面积是( )
A. 15 cm2
B. 18 cm2
C. 21 cm2
D. 24 cm2 举一反三B 2. 已知某几何体的三视图如图29-2-10所示,则该几何体的体积为( )B 1. 三视图的摆放规则:俯视图放在主视图的下面,长度与主视图的长度一样;左视图放在主视图的右面,高度与主视图的高度一样,宽度与俯视图的宽度一样,可简记为“长对正;高平齐;宽相等”.
2. 在画物体的三视图时,对看得见的轮廓线用实线画出,而对看不见的轮廓线要用虚线画出.在三种视图中,主视图反映的是物体的长和高,俯视图反映的是物体的长和宽,左视图反映的是物体的宽和高.因此,在画三视图时,对应部分的长度要相等. 方法规律 7. (6分)如图KT29-2-6,
是一个由若干个棱长相等的正方
体构成的几何体的三视图.
(1)请写出构成这个几何体的
正方体个数;
(2)请根据图中所标的尺寸,
计算这个几何体的表面积. 解:(1)5个.
(2)S表=5×6a2-2×5a2=20a2. 8. (6分)如图KT29-2-7
是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据图中所示数据计算
这个几何体的表面积;
(3)如果一只蚂蚁要从这个
几何体中的点B出发,沿表面爬
到AC的中点D,请你求出这个线路的最短路程. 解:(1)圆锥.
(2)S表=S扇形+S圆=πrl+
πr2=12π+4π=16π(cm2).
(3)如答图29-2-2将圆锥侧面展开,线段BD为所求的最短路程.
由条件得,∠BAB′=120°,C为弧BB′中点,所以BD= (cm).
