人教版初中数学九年级下册同步课件 27.1 图形的相似(共30张PPT)
文档属性
| 名称 | 人教版初中数学九年级下册同步课件 27.1 图形的相似(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 542.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-05 00:00:00 | ||
图片预览











文档简介
课件30张PPT。第二十七章
相 似27.1
图形的相似 新知1 图形的相似
1. 两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
2. 全等形可以看成是一种特殊的相似图形,不仅形状相同,大小也相同.
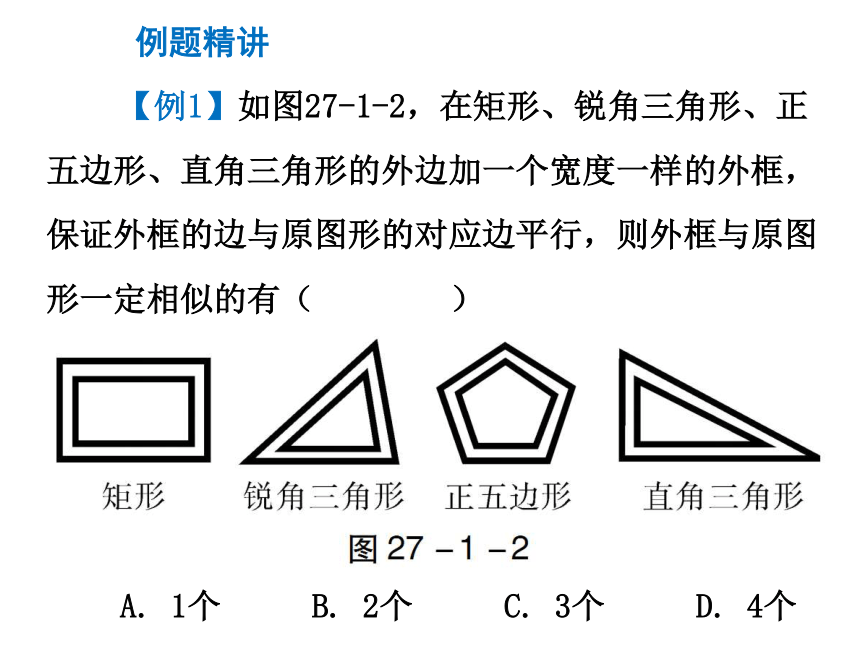
3. 判断两个图形是否相似,就看这两个图形是不是形状相同,与其他因素无关. 【例1】如图27-1-2,在矩形、锐角三角形、正五边形、直角三角形的外边加一个宽度一样的外框,保证外框的边与原图形的对应边平行,则外框与原图形一定相似的有( )
A. 1个 B. 2个 C. 3个 D. 4个 例题精讲 解析 第一个图形是同一个矩形的放大或缩小,是相似图形;第二个图形是同一个锐角三角形的放大或缩小,也是相似图形;第三个是同一个正五边形的放大或缩小,也是相似图形;最后一个是同一个直角三角形的放大或缩小,也是相似图形.
答案 D 1. 对一个图形进行放缩时,下列说法正确的是( )
A. 图形中线段的长度与角的大小都保持不变
B. 图形中线段的长度与角的大小都会改变
C. 图形中线段的长度保持不变,角的大小可以
改变
D. 图形中线段的长度可以改变,角的大小保持
不变 举一反三D 2. 下列判断正确的是( )
A. 所有的直角三角形都相似
B. 所有的等腰直角三角形都相似
C. 所有的菱形都相似
D. 所有的矩形都相似B 新知2 成比例线段 1. 判断四条线段是否成比例,只要把四条线段按大小顺序排列好,判断前两条线段之比与后两条线段之比是否相等即可.
2. 如果a∶b=b∶c,则b2=ac,线段b叫做线段a,c的比例中项.
3. 在有顺序的比例式a∶b=c∶d中,d叫做a,b,c的第四比例项. 5. 黄金分割:如图27-1-3所示,把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即 ),叫做把这条线段AB黄金分割,点C叫做线段AB的黄金分割点.
其中AC= AB≈0.618AB,并且线段AB的黄金分割点有两个. 【例2】如图27-1-4.
(1)根据图示求线段比:
(2)试指出图中4条成比例的线段. 例题精讲 解析 线段的比即为线段的长度比. 由图可知AC,CD,CB,DB的长分别为1 cm,2 cm,6 cm,4 cm,这样便可求出相关线段的比.
解 1. 下列各组中四条线段成比例的是( )
A. 4 cm,2 cm,1 cm,3 cm
B. 1 cm,2 cm,3 cm,5 cm
C. 3 cm,4 cm,5 cm,6 cm
D. 1 cm,2 cm,2 cm,4 cm 举一反三D 2. 已知线段a=1 cm,c=4 cm,x是a,c的比例中项,则x等于( )
A. 4 cm B. 2 cm
C.-2 cm D.±2 cmB 3. 如果四条线段a,b,c,d构成ab=cd,m>0,则下面推理正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个C 新知3 相似多边形的特征 1. 对应角相等,对应边成比例的两个多边形叫做相似多边形,相似多边形对应边的比叫做相似比.
2. 相似多边形的周长比等于相似比,面积比等于相似比的平方,对应线段比等于相似比. 【例3】已知图27-1-5中的两个四边形相似,找出其中成比例的线段,并用比例式表示. 例题精讲 解析 由于两个四边形相似,所以对应角相等,对应边成比例,可得
答案 1. 两个相似五边形,一组对应边的长分别为3 cm和4.5 cm,如果它们的面积之和是78 cm2,则较大的五边形面积是( )cm2.( )
A. 44.8 B. 52 C. 54 D. 42 举一反三C 2. 已知如图27-1-6,一张矩形报纸ABCD的长AB=a cm,宽BC=b cm,E,F分别为AB,CD的中点.若矩形AEFD与矩形ABCD相似,则a∶b等于( )A 新知4 两个多边形相似的判别方法 【例2】仔细观察图27-1-7,看看四边形ABCD与四边形A′B′C′D′是否相似. 如果
相似,求它们的相似比;如果
不相似,请说明理由. 例题精讲 解析 通过观察可以发现,四边形ABCD的各边的长度分别是四边形A′B′C′D′的各边长的2倍,各对应边互相平行(AB与A′B′在同一直线上),因此两四边形的对应角相等. 解 四边形ABCD与四边形A′B′C′D′相似.
∠DAB=∠D′A′B′,∠ABC=∠A′B′C′,
∠BCD=∠B′C′D′,∠CDA=∠C′D′A′,
∴四边形ABCD与四边形A′B′C′D′相似,且相似比为2. 1. 图27-1-8中,有三个矩形,其中相似的是( )
A. 甲和乙 B. 甲和丙
C. 乙和丙 D. 没有相似的矩形 举一反三B 2. 如图27-1-9,把一个长方形划分为5个全等的小长方形,若要使每一个小长方形与原长方形相似,则原长方形的边a,b应满足的条件是( )
C 3. 一个五边形的各边长为2,3,4,5,6,另一个与它相似的五边形的最长边是12,则最短边为( )
A. 4 B. 5 C. 6 D. 8 A 1. 两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.判断两个图形是否相似,就是看这两个图形是不是形状相同,与其他因素无关.
2. 对于四条线段a,b,c,d,如果其中两条线段的长度的比与另两条线段的长度的比相等,即a∶b=c∶d,那么这四条线段叫做成比例线段,简称比例线段.
3. 相似多边形的性质:相似多边形的对应角相等,对应边成比例.
方法规律 7.(6分)在参加北京申办2008年奥运活动中,某班同学争取到制作若干面彩旗的任务,如果有两边长分别为a(其中a>1)和1的一块矩形绸布,要将它剪出三面彩旗(面料没有剩余),使每面彩旗的长和宽之比与原绸布的长和宽之比相同,画出两种不同的剪裁方法的示意图,并写出相应的a的值(不写计算过程). 解:示意图和a的值如答图27-1-1所示. 8. (6分)已知四边形ABCD与四边形A′B′C′D′
相似,且AB∶BC∶CD∶DA=20∶15∶9∶8,四边形A′B′C′D′的周长为26,求四边形A′B′C′D′
各边的长. 解:∵四边形ABCD与四边形A′B′C′D′相似,且AB∶BC∶CD∶DA=20∶15∶9∶8,
∴A′B′∶B′C′∶C′D′∶D′A′=20∶15∶9∶8.
设A′B′=20x,B′C′=15x,C′D′=9x,D′A′=8x,
由四边形A′B′C′D′的周长为26,得
20x+15x+9x+8x=26,解得x= .
∴A′B′=10,B′C′=7.5,C′D′=4.5,D′A′=4.
相 似27.1
图形的相似 新知1 图形的相似
1. 两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
2. 全等形可以看成是一种特殊的相似图形,不仅形状相同,大小也相同.
3. 判断两个图形是否相似,就看这两个图形是不是形状相同,与其他因素无关. 【例1】如图27-1-2,在矩形、锐角三角形、正五边形、直角三角形的外边加一个宽度一样的外框,保证外框的边与原图形的对应边平行,则外框与原图形一定相似的有( )
A. 1个 B. 2个 C. 3个 D. 4个 例题精讲 解析 第一个图形是同一个矩形的放大或缩小,是相似图形;第二个图形是同一个锐角三角形的放大或缩小,也是相似图形;第三个是同一个正五边形的放大或缩小,也是相似图形;最后一个是同一个直角三角形的放大或缩小,也是相似图形.
答案 D 1. 对一个图形进行放缩时,下列说法正确的是( )
A. 图形中线段的长度与角的大小都保持不变
B. 图形中线段的长度与角的大小都会改变
C. 图形中线段的长度保持不变,角的大小可以
改变
D. 图形中线段的长度可以改变,角的大小保持
不变 举一反三D 2. 下列判断正确的是( )
A. 所有的直角三角形都相似
B. 所有的等腰直角三角形都相似
C. 所有的菱形都相似
D. 所有的矩形都相似B 新知2 成比例线段 1. 判断四条线段是否成比例,只要把四条线段按大小顺序排列好,判断前两条线段之比与后两条线段之比是否相等即可.
2. 如果a∶b=b∶c,则b2=ac,线段b叫做线段a,c的比例中项.
3. 在有顺序的比例式a∶b=c∶d中,d叫做a,b,c的第四比例项. 5. 黄金分割:如图27-1-3所示,把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即 ),叫做把这条线段AB黄金分割,点C叫做线段AB的黄金分割点.
其中AC= AB≈0.618AB,并且线段AB的黄金分割点有两个. 【例2】如图27-1-4.
(1)根据图示求线段比:
(2)试指出图中4条成比例的线段. 例题精讲 解析 线段的比即为线段的长度比. 由图可知AC,CD,CB,DB的长分别为1 cm,2 cm,6 cm,4 cm,这样便可求出相关线段的比.
解 1. 下列各组中四条线段成比例的是( )
A. 4 cm,2 cm,1 cm,3 cm
B. 1 cm,2 cm,3 cm,5 cm
C. 3 cm,4 cm,5 cm,6 cm
D. 1 cm,2 cm,2 cm,4 cm 举一反三D 2. 已知线段a=1 cm,c=4 cm,x是a,c的比例中项,则x等于( )
A. 4 cm B. 2 cm
C.-2 cm D.±2 cmB 3. 如果四条线段a,b,c,d构成ab=cd,m>0,则下面推理正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个C 新知3 相似多边形的特征 1. 对应角相等,对应边成比例的两个多边形叫做相似多边形,相似多边形对应边的比叫做相似比.
2. 相似多边形的周长比等于相似比,面积比等于相似比的平方,对应线段比等于相似比. 【例3】已知图27-1-5中的两个四边形相似,找出其中成比例的线段,并用比例式表示. 例题精讲 解析 由于两个四边形相似,所以对应角相等,对应边成比例,可得
答案 1. 两个相似五边形,一组对应边的长分别为3 cm和4.5 cm,如果它们的面积之和是78 cm2,则较大的五边形面积是( )cm2.( )
A. 44.8 B. 52 C. 54 D. 42 举一反三C 2. 已知如图27-1-6,一张矩形报纸ABCD的长AB=a cm,宽BC=b cm,E,F分别为AB,CD的中点.若矩形AEFD与矩形ABCD相似,则a∶b等于( )A 新知4 两个多边形相似的判别方法 【例2】仔细观察图27-1-7,看看四边形ABCD与四边形A′B′C′D′是否相似. 如果
相似,求它们的相似比;如果
不相似,请说明理由. 例题精讲 解析 通过观察可以发现,四边形ABCD的各边的长度分别是四边形A′B′C′D′的各边长的2倍,各对应边互相平行(AB与A′B′在同一直线上),因此两四边形的对应角相等. 解 四边形ABCD与四边形A′B′C′D′相似.
∠DAB=∠D′A′B′,∠ABC=∠A′B′C′,
∠BCD=∠B′C′D′,∠CDA=∠C′D′A′,
∴四边形ABCD与四边形A′B′C′D′相似,且相似比为2. 1. 图27-1-8中,有三个矩形,其中相似的是( )
A. 甲和乙 B. 甲和丙
C. 乙和丙 D. 没有相似的矩形 举一反三B 2. 如图27-1-9,把一个长方形划分为5个全等的小长方形,若要使每一个小长方形与原长方形相似,则原长方形的边a,b应满足的条件是( )
C 3. 一个五边形的各边长为2,3,4,5,6,另一个与它相似的五边形的最长边是12,则最短边为( )
A. 4 B. 5 C. 6 D. 8 A 1. 两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.判断两个图形是否相似,就是看这两个图形是不是形状相同,与其他因素无关.
2. 对于四条线段a,b,c,d,如果其中两条线段的长度的比与另两条线段的长度的比相等,即a∶b=c∶d,那么这四条线段叫做成比例线段,简称比例线段.
3. 相似多边形的性质:相似多边形的对应角相等,对应边成比例.
方法规律 7.(6分)在参加北京申办2008年奥运活动中,某班同学争取到制作若干面彩旗的任务,如果有两边长分别为a(其中a>1)和1的一块矩形绸布,要将它剪出三面彩旗(面料没有剩余),使每面彩旗的长和宽之比与原绸布的长和宽之比相同,画出两种不同的剪裁方法的示意图,并写出相应的a的值(不写计算过程). 解:示意图和a的值如答图27-1-1所示. 8. (6分)已知四边形ABCD与四边形A′B′C′D′
相似,且AB∶BC∶CD∶DA=20∶15∶9∶8,四边形A′B′C′D′的周长为26,求四边形A′B′C′D′
各边的长. 解:∵四边形ABCD与四边形A′B′C′D′相似,且AB∶BC∶CD∶DA=20∶15∶9∶8,
∴A′B′∶B′C′∶C′D′∶D′A′=20∶15∶9∶8.
设A′B′=20x,B′C′=15x,C′D′=9x,D′A′=8x,
由四边形A′B′C′D′的周长为26,得
20x+15x+9x+8x=26,解得x= .
∴A′B′=10,B′C′=7.5,C′D′=4.5,D′A′=4.
